目录
摘要
本篇文章继续学习尚硅谷深度学习教程，学习内容是反向传播算法的计算图和链式法则。
反向传播算法
反向传播（Backward Propagation或Back Propagation，BP算法）指的是计算神经网络参数梯度的方法。简言之，该方法根据微积分中的链式法则，按相反的顺序从输出层到输入层遍历网络。该算法存储了计算某些参数梯度时所需的任何中间变量。
1.计算图
计算图将计算过程用图表示出来。这里说的图是数据结构中的图，通过多个节点和边表示（连接节点的直线称为边）。
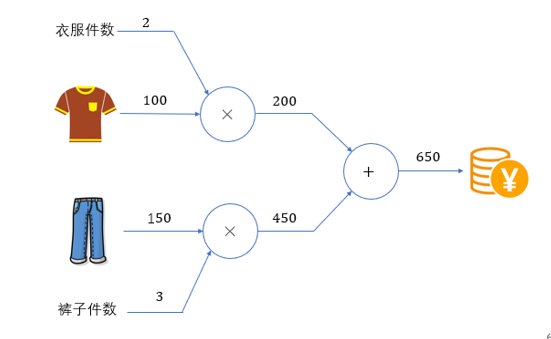
如上就是 100 × 2+150 × 3=650 的计算图表示。
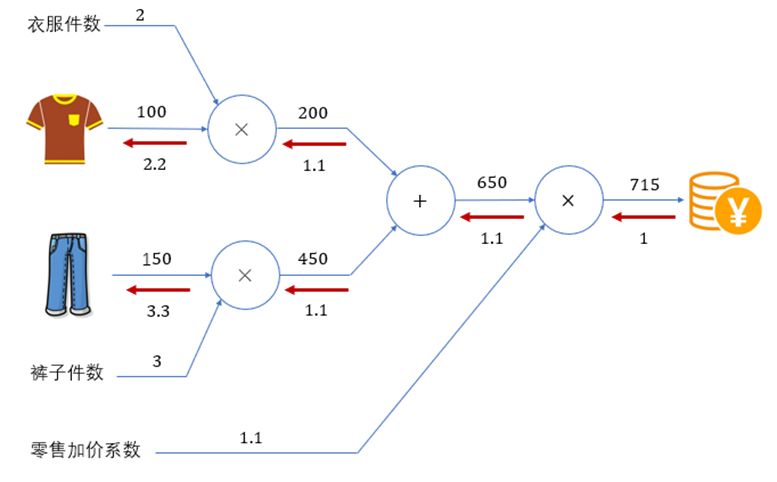
计算图的基本计算原则，就是从输入出发、按照箭头方向，从左到右依次进行计算，最终得到输出结果。这个过程，其实就是前向传播（forward）。计算图的特点是可以通过传递"局部计算"获得最终结果。即只需根据与自己相关的信息输出接下来的结果。无论全局的计算有多么复杂，各个节点所要做的就是进行局部计算并传递计算结果，最终得出全局的复杂计算的结果。如果增加更多的计算环节，比如再乘以一个"零售加价系数"，计算图如下所示。
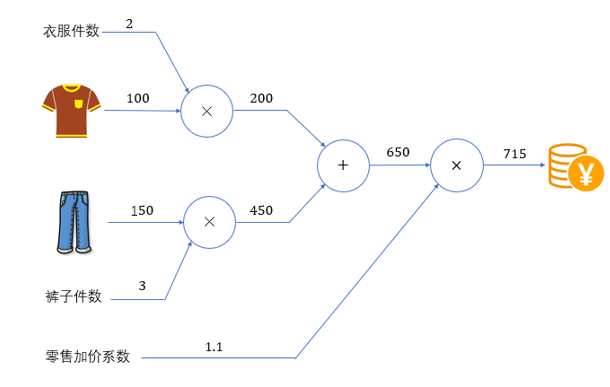
如果我们进一步考虑，当衣服的价格上涨（输入变化）时，会多大程度上影响最后要支付的金额（输出结果）？
将输入的衣服价格记为x ，输出的支付金额记为L ，这其实就是要求导数值 ∂L ∂x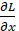 
。在计算图上，我们可以利用反向（从右到左）的传递来方便地计算导数。这个过程，就可以叫做 反向传播（backward）。
2.链式法则
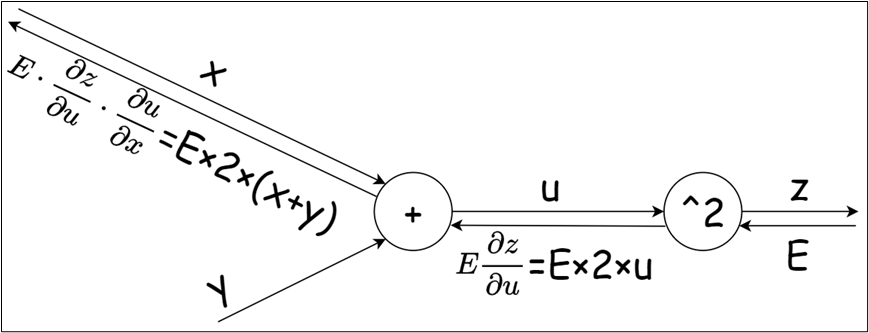
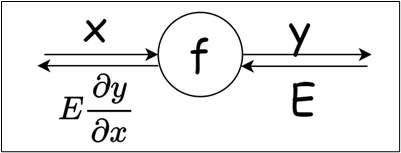
反向传播将局部导数向反方向传递，传递的原理基于链式法则。反向传播时将信号乘以节点的局部导数然后传递给下一个节点。
对于复合函数 ，令u=x+y ，则
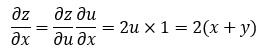
现用计算图表示：
