笔记：Cross Modal Fusion-Mamba

[一. 引言](#一. 引言)

[二. 网络总览](#二. 网络总览)

[三. Mamba Block 的结构](#三. Mamba Block 的结构)

[3.1. SSCS（State Space Channel Swapping）Module](#3.1. SSCS（State Space Channel Swapping）Module)

[3.1.1. Channel swapping](#3.1.1. Channel swapping)

[3.1.2. VSS（Vision State Space）block](#3.1.2. VSS（Vision State Space）block)

[3.1.3. VSS代码分析](#3.1.3. VSS代码分析)

[3.2. DSSF（Dual State Space Fusion）](#3.2. DSSF（Dual State Space Fusion）)

一. 引言

该论文是基于Yolov5的改进型红外可见光融合目标检测方法，对于无Yolo和CNN基础的读者可以参考：

笔记：对yolov8网络代码的学习_ultralytics哪个函数将 yaml文件中的backbone: [-1, 1, conv, [-CSDN博客

基于Yolo的图像识别中的特征融合_yolo 特征融合-CSDN博客

笔记：Mamba初了解_曼巴隐空间ssm-CSDN博客

论文源： 10.1109/TMM.2025.3599020

代码源： https://github.com/EhanDong/Fusion-Mamba

注：本笔记并非对全文的复述，而是重点对其网络结构和模块（尤其是即插即用算子Mamba Block）进行学习和理解。

二. 网络总览

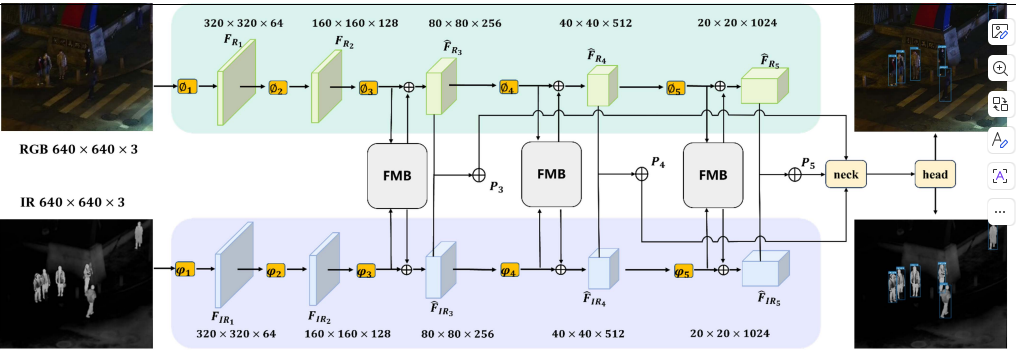
该示意图表示了两个输入RGB（可见光） 和IR（红外光），RGB主要提供纹理 / 语义，IR：主要提供目标 / 轮廓 / 热信息。

两种输入相互独立并采用典型的CNN金字塔style进行采样。当采样到第二层开始，每层采样后都接入Mamba Block进行特征交互，将交互结果接入Neck辅助特征融合，最终进行重构通过head生成检测结果。

三. Mamba Block 的结构

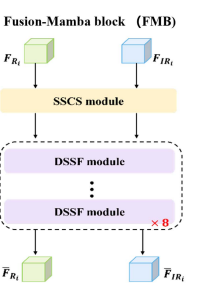
Mamba Block可细分为两大模块，SSCS 和 DSSF 。其中DSSF 堆叠8次在SSCS之后。

3.1. SSCS（State Space Channel Swapping）Module

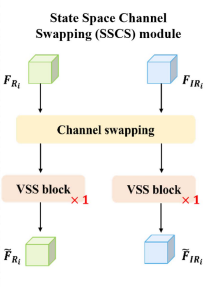
3.1.1. Channel swapping

Channel swapping（通道交换）的本质 是在进入状态空间（Mamba）建模之前，主动打破 RGB / IR 通道的模态纯净性 ，让每一个分支在"还没深度融合之前"就已经携带对方模态的局部表达。

文中给出整体表达式为：

也就是说，假设两个模态的描述某同一目标的特征如下：

则经过swapping后，我们可以得到情况：

注意：这个Swapping不是随机，不是学习到的注意力，而是结构性、可控的通道级重组。

为什么要在浅层做通道交换？

给后续的增强做铺垫，在进入状态空间建模之前，先让 RGB 特征"带一点 IR 的眼睛"，让 IR 特征"带一点 RGB 的视角"。

传统方法（不做swapping）会在融合阶段直接进行concat或者进入attention/mamba模块融合，这会使得每个分支仍然保留强烈的模态偏置（强纹理/背景/光照和强目标/热轮廓/前景）。

为什么只换通道而不做attention？

首先要提到Channel Swapping 的三个优点：

低开销（只是 split + concat），不会引入额外噪声。

不做显式加权，避免伪目标放大，attention可能会在浅层把噪声当目标。

为后续 DSSF 的"状态空间融合"做铺垫，SSCS偏引导，DSSF重融合。

3.1.2. VSS（Vision State Space）block

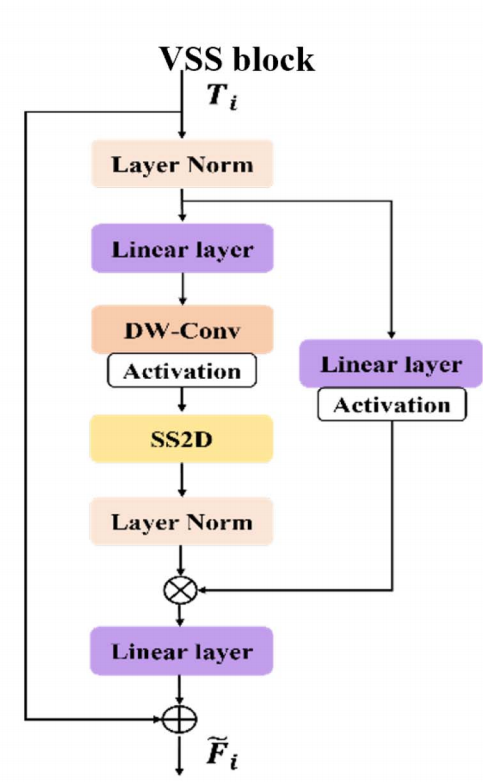
VSS block 是把2D 视觉特征映射到"可控的状态空间序列"，并用线性复杂度建模全局依赖的核心算子。在整个模块中负责在状态空间中传播与整合信息。

注意：圈里 "+"：残差相加 / 状态融合（additive fusion），圈里 "×"：门控调制 / 逐元素缩放（multiplicative gating）

VSS block的输入和输出规模相同 ，但是整体输出时每个位置的特征已经具备 全局感受野。

VSS block的流程可抽象为：

bash 复制代码

→ LayerNorm
→ Linear projection
→ Depthwise Conv
→ Activation
→ SS2D（核心）
→ LayerNorm
→ Linear projection
→ Residual

对每个组件进行逐个解释：

（1）LayerNorm（前）

作用：

稳定状态空间输入

避免不同通道在 SSM 中数值爆炸

这是 状态空间模型的必要前处理。

（2）Linear Projection（前）

作用：

调整通道维度

将 CNN-style feature 映射到 SSM 友好的表示空间

（3）Depthwise Conv（DW-Conv）

这是很多人忽略但非常关键的一步。

作用：

注入 局部空间 inductive bias

补偿 SSM 对局部细节不敏感的问题

这一步保证：

VSS 不是"纯序列模型"，而是 视觉友好的状态空间模块。

（4）Activation（激活函数）

提供非线性

为 SSM 的 gating / selective mechanism 做准备

（5）SS2D（核心）

这是 VSS 的重点

这一层：

建模 长程依赖

在 状态空间中传播信息

不显式计算 token-token attention

（6）LayerNorm（后）

（7）Linear Projection（后）

作用：

将状态空间输出重新投影回特征空间

方便后续 residual / fusion

（7）Residual Connection

作用：

保留原始局部信息

防止状态空间过度平滑

功能上 ，VSS 完成了一个 2D→1D→2D 的过程，在这个过程中，二维特征被展开为结构化的一维序列以适配 Mamba 的状态空间建模，并在完成长程信息交互后恢复为二维表示，从而实现与 CNN/YOLO 等二维网络结构的无缝对接。

3.1.3. VSS代码分析

代码见：项目源文件\models\common.py

python 复制代码

class VSSBlock(nn.Module):
    def __init__(
        self,
        hidden_dim: int = 0,  # 通道数 C（该 block 通常接收 NHWC: (B,H,W,C)）
        drop_path: float = 0,  # DropPath 概率（stochastic depth）
        norm_layer: Callable[..., torch.nn.Module] = partial(nn.LayerNorm, eps=1e-6),  # 归一化层构造器（默认 LN）
        attn_drop_rate: float = 0,  # SS2D 内部 dropout（作者沿用 attn_drop 命名）
        d_state: int = 16,  # SSM/Mamba 的状态维度（控制容量/开销）
        **kwargs,  # 透传给 SS2D 的其它超参（如 expand、d_conv、dt_rank 等）
    ):
        super().__init__()

        # Pre-Norm：先归一化再做主算子（稳定训练）
        self.ln_1 = norm_layer(hidden_dim)

        # 核心模块：SS2D（把 2D 特征序列化后用 selective_scan/Mamba 做状态空间建模，再回到 2D）
        self.self_attention = SS2D(
            d_model=hidden_dim,     # 输入/输出通道
            dropout=attn_drop_rate, # dropout 超参
            d_state=d_state,        # 状态维度超参
            **kwargs
        )

        # DropPath：训练时随机丢弃整条残差分支（正则化）
        self.drop_path = DropPath(drop_path)

    def forward(self, input: torch.Tensor):
        # input: (B, H, W, C)  (通常由外部 permute 得到)
        d = self.ln_1(input)              # LN 归一化（Pre-Norm）
        c = self.self_attention(d)        # SS2D：全局依赖建模（核心计算）
        y = self.drop_path(c)             # DropPath 正则
        x = input + y                     # 残差连接（保持信息与梯度稳定）
        return x                          # output: (B, H, W, C)

结构上：VSS就是标准化 → 通道映射（非严格降维） → 局部增强 + SSM（DW-Conv + SS2D） → 通道映射回原维度 → 正则化/门控 → 残差。

输入用的是归一化，为什么输出用的是DropPath正则化？

LN解决的是数值稳定问题

SSM 模型对输入数值尺度非常敏感，如果不同通道或不同位置的特征幅值差异过大，状态递推过程容易出现梯度爆炸或过度衰减，从而导致训练不稳定。
python 复制代码
state_t = f(state_{t-1}, input_t)
上面是状态递推的经典形式，如果input大小不一且差别过大，会发生梯度爆炸会发生梯度爆炸或梯度消失，导致隐藏状态在递推过程中数值发散或迅速衰减，从而引起训练不稳定、收敛变慢甚至直接 NaN。

DropPath 不是"算子"，是正则化策略
python 复制代码
y = DropPath(F(x))
output = x + y
训练时：以一定概率直接让 F(x)=0。

推理时：DropPath 关闭

本质上是一个随机的结构级门控，作用在残差分支上，通过随机启用/禁用该分支来防止模型过度依赖某个强模块，从而抑制过拟合。

其实在class VSSBlock没有通道映射，也没有完整的核心模块，因此我们看到class SS2D：

python 复制代码

class SS2D(nn.Module):
    def __init__(
        self,
        d_model,             # 输入/输出通道数 C（外部看到的维度）
        d_state=16,          # SSM 状态维度 N（"记忆容量/状态大小"）
        # d_state="auto",    # 可选：自动按 d_model 估计状态维度
        d_conv=3,            # DW-Conv 的 kernel size（局部建模范围）
        expand=2,            # 通道扩展倍率（内部维度 d_inner = expand * d_model）
        dt_rank="auto",      # dt 低秩参数的 rank（控制 dt 参数化容量/开销）
        dt_min=0.001,        # dt 初始化的最小值（时间步/步长的下界）
        dt_max=0.1,          # dt 初始化的最大值（时间步/步长的上界）
        dt_init="random",    # dt 初始化策略（随机/常数等）
        dt_scale=1.0,        # dt 初始化缩放因子
        dt_init_floor=1e-4,  # dt 初始化的数值下限（避免过小导致数值问题）
        dropout=0.,          # 输出 dropout 概率（SS2D 末端正则）
        conv_bias=True,      # DW-Conv 是否带 bias
        bias=False,          # Linear 的 bias 开关（in/out proj 等）
        device=None,         # 放到哪个 device
        dtype=None,          # 参数 dtype
        **kwargs,            # 预留扩展参数
    ):
        factory_kwargs = {"device": device, "dtype": dtype}  # 统一传给层构造函数的设备/精度
        super().__init__()

        self.d_model = d_model        # 记录外部通道维度
        self.d_state = d_state        # 记录 SSM 状态维度
        # self.d_state = ...           # auto 逻辑（注释掉的版本）
        self.d_conv = d_conv          # 记录 DW-Conv kernel size
        self.expand = expand          # 记录通道扩展倍率
        self.d_inner = int(self.expand * self.d_model)  # 内部通道维度（通常 > d_model）
        self.dt_rank = math.ceil(self.d_model / 16) if dt_rank == "auto" else dt_rank
        # dt_rank：自动时随 d_model 增长；否则用你指定的 rank

        # 输入投影：把 (C=d_model) 映射到 (2*d_inner)
        # 通常用于 split 成两路：一路做主干 x，一路做门控 z（后面会用 silu(z)）
        self.in_proj = nn.Linear(self.d_model, self.d_inner * 2, bias=bias, **factory_kwargs)

        # 深度可分离卷积（DW-Conv）：只在各通道内做局部空间卷积，补局部感受野
        # groups=self.d_inner => depthwise
        self.conv2d = nn.Conv2d(
            in_channels=self.d_inner,
            out_channels=self.d_inner,
            groups=self.d_inner,          # depthwise
            bias=conv_bias,
            kernel_size=d_conv,           # 局部窗口大小
            padding=(d_conv - 1) // 2,    # 保持 H,W 尺寸不变
            **factory_kwargs,
        )

        self.act = nn.SiLU()  # 激活函数（门控/非线性常用 SiLU）

        # x_proj：为 4 个方向（K=4）各配一套线性投影，用来从特征生成 SSM 所需参数
        # 输出维度 = dt_rank + 2*d_state，通常会切成：dt相关 + B + C（SSM参数）
        self.x_proj = (
            nn.Linear(self.d_inner, (self.dt_rank + self.d_state * 2), bias=False, **factory_kwargs),
            nn.Linear(self.d_inner, (self.dt_rank + self.d_state * 2), bias=False, **factory_kwargs),
            nn.Linear(self.d_inner, (self.dt_rank + self.d_state * 2), bias=False, **factory_kwargs),
            nn.Linear(self.d_inner, (self.dt_rank + self.d_state * 2), bias=False, **factory_kwargs),
        )

        # 把四个方向的权重堆成一个大参数张量，便于后续一次性计算/加速
        # 形状：(K=4, out_dim, d_inner) ------ 代码注释写 (K=4, N, inner) 这里 N 指 out_dim
        self.x_proj_weight = nn.Parameter(torch.stack([t.weight for t in self.x_proj], dim=0))
        del self.x_proj  # 删除 ModuleList/tuple，避免重复注册；保留合并后的权重参数

        # dt_projs：4 个方向各一套 dt 的投影层（dt 的低秩参数化）
        # dt_init(...) 通常会返回一个 Linear(rank -> d_inner) 或类似结构
        self.dt_projs = (
            self.dt_init(self.dt_rank, self.d_inner, dt_scale, dt_init, dt_min, dt_max, dt_init_floor, **factory_kwargs),
            self.dt_init(self.dt_rank, self.d_inner, dt_scale, dt_init, dt_min, dt_max, dt_init_floor, **factory_kwargs),
            self.dt_init(self.dt_rank, self.d_inner, dt_scale, dt_init, dt_min, dt_max, dt_init_floor, **factory_kwargs),
            self.dt_init(self.dt_rank, self.d_inner, dt_scale, dt_init, dt_min, dt_max, dt_init_floor, **factory_kwargs),
        )

        # 同样把四个方向的 dt 投影层参数打包成大张量
        # weight: (K=4, d_inner, rank)；bias: (K=4, d_inner)
        self.dt_projs_weight = nn.Parameter(torch.stack([t.weight for t in self.dt_projs], dim=0))
        self.dt_projs_bias = nn.Parameter(torch.stack([t.bias for t in self.dt_projs], dim=0))
        del self.dt_projs  # 删除原子模块，保留合并参数

        # A_logs：SSM 的 A 参数（通常以 log 参数化，保证稳定性/约束）
        # copies=4 表示给 4 个方向各复制一份；merge=True 表示合并存储
        # 形状注释：(K=4, D, N) 这里 D≈d_inner，N≈d_state（按作者约定）
        self.A_logs = self.A_log_init(self.d_state, self.d_inner, copies=4, merge=True)

        # Ds：SSM 的 D 参数（skip/残差项或通道缩放项），同样做 4 方向复制并合并
        self.Ds = self.D_init(self.d_inner, copies=4, merge=True)

        # selective_scan_fn：底层 SSM 扫描算子（这里注释掉，可能在 forward_core 内部调用）
        # self.selective_scan = selective_scan_fn

        self.forward_core = self.forward_corev0  # 指定核心 forward 实现版本（v0）

        self.out_norm = nn.LayerNorm(self.d_inner)  # 输出归一化（在投影回 d_model 前稳定数值）
        self.out_proj = nn.Linear(self.d_inner, self.d_model, bias=bias, **factory_kwargs)  # 回投影：d_inner -> d_model
        self.dropout = nn.Dropout(dropout) if dropout > 0. else None  # 输出 dropout（可选）

定义上，SS2D完成了这些操作：

步骤 1：二维 → 多个一维序列

对一个特征图，沿 四个方向扫描：

左 → 右

右 → 左

上 → 下

下 → 上

得到 4 条 1D 序列：

步骤 2：每条序列独立通过 SSM（Mamba）

对每个方向：

使用 Selective State Space Model

时间复杂度：

步骤 3：序列 → 2D 特征重建

将 4 个方向的输出重新映射回 2D

做等权融合

最终得到：

代码上，它还包括：

1. 通道扩展与门控 （in_proj 将特征映射到 2*d_inner 并 split 出主分支/门控分支）

2. DW-Conv 的局部增强 （conv2d 提供局部归纳偏置）、为四个方向分别生成 SSM 参数（x_proj_weight/dt_projs_* 产生 dt,B,C 等）

3. 稳定性相关参数化 （A_logs 的 log 参数化与 D 项）

4. 输出端的归一化与回投影 （out_norm + out_proj，可选 dropout）

为什么不直接用Mamba？

原始 Mamba / SSM 适用于：

1D sequence（NLP）

但视觉特征是：

2D grid

空间邻接关系极强

所以论文引入 SS2D（2D Selective Scan）。

3.2. DSSF（Dual State Space Fusion）

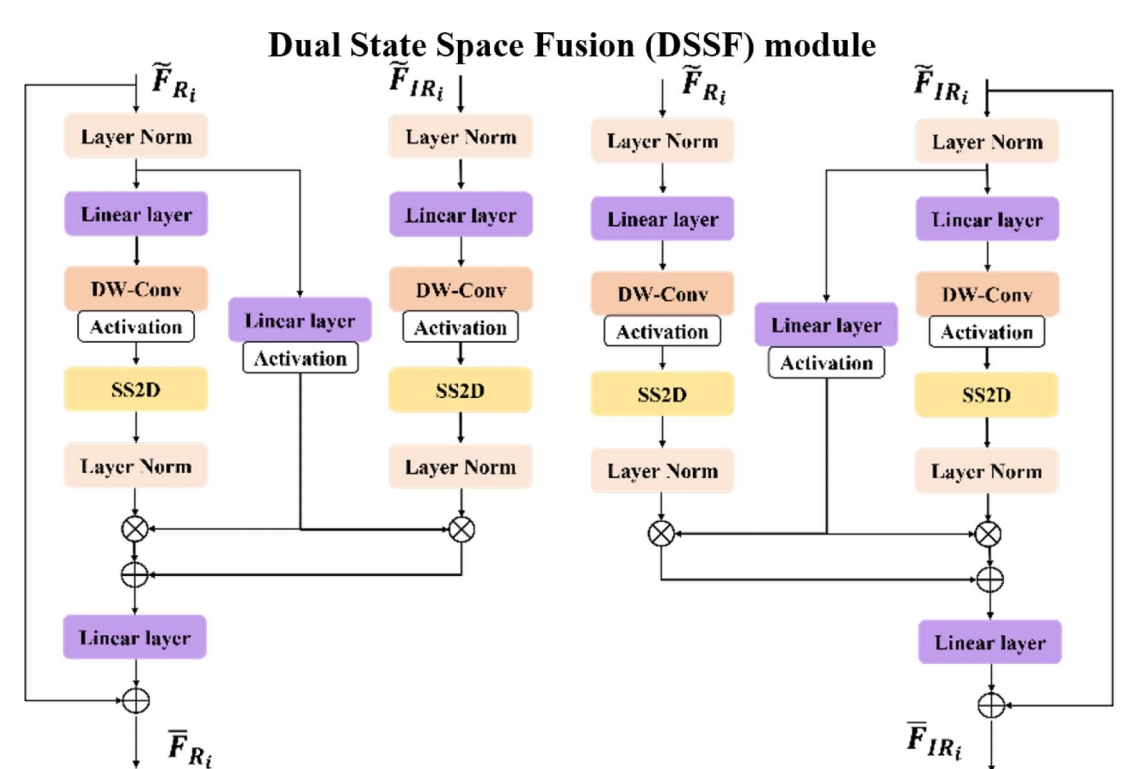
DSSF 的核心结构：两个"VSS-like 分支 + 交叉耦合"

图左边的 DSSF：它其实由两套几乎对称的子结构组成（上面那套处理 RGB，下面那套处理 IR），每套内部都长得像一个 VSS block（LN→Linear→DWConv+Act→SS2D→LN），但关键差异是：

中间有"交叉连接"（cross coupling） ：

RGB 分支的某个中间表示会加到 IR 分支，IR 分支的某个中间表示也会加到 RGB 分支。

这就是 "Dual + Fusion" 的本质：双状态空间 + 状态层交互。

每个分支 SS2D 后面都有一个 ⊕，并且这两个 ⊕ 之间用线连起来------这就是"Dual Fusion"。

可以把它理解为：

RGB 分支得到一个"状态增强特征"

IR 分支得到一个"状态增强特征"

简而言之，VSS 是一个基于 Mamba/SSM 的单流全局特征建模模块，用于在不显式计算 attention 的情况下完成长程依赖建模。DSSF 采用双分支状态空间建模策略，分别以 RGB 和 IR 特征作为主干输入 ，并在状态增强阶段引入来自另一模态的辅助信息 ，从而实现对称且受控的跨模态融合。对称的 DSSF 结构确保跨模态融合不依赖于固定的主模态假设，使模型能够在不同场景下自适应地利用 RGB 或 IR 作为主导信息源。

为什么DSSF需要堆叠8次？

如果 只做一次 DSSF：

等价于一次"强跨模态扰动"

很容易：引入伪响应，把噪声直接传播到全局

CrossMamba 的思路是：

少量、多次、逐步地让两种模态在状态空间里互相"影响"

另外，SSM 的优势在"多步传播"，不是单步映射。
python 复制代码
state_{t} = f(state_{t-1}, input_t)
一次 DSSF ≈ 一次状态更新

多次 DSSF ≈ 多次状态演化

堆叠的意义是：

让跨模态信息在多个状态更新阶段逐渐渗透，而不是一次性对齐。

这对抑制跨模态噪声非常关键。

深度问题

太浅（1--2）交互不足，退化为弱融合

中等（4--8）信息充分传播，训练稳定

过深（>12）计算重、梯度噪声累积、收益递减

深度	问题
太浅（1--2）	交互不足，退化为弱融合
中等（4--8）	信息充分传播，训练稳定
过深（>12）	计算重、梯度噪声累积、收益递减