数据结构算法学习：LeetCode热题100-栈篇（有效的括号、最小栈、字符串解码、每日温度、柱状图中最大的矩形）

文章目录

• 简介
• [20. 有效的括号](#20. 有效的括号)
• [155. 最小栈](#155. 最小栈)
• • [394. 字符串解码](#394. 字符串解码)
• [739. 每日温度](#739. 每日温度)
• [84. 柱状图中最大的矩形](#84. 柱状图中最大的矩形)
• 个人学习总结

简介

本篇博客聚焦于 LeetCode 热题 100 中关于"栈"这一核心数据结构的经典应用。栈作为一种"后进先出"（LIFO）的线性结构，在处理括号匹配、层级字符串解码、查找边界以及面积计算等问题时发挥着关键作用。本文将深入剖析"有效的括号"、"最小栈"、"字符串解码"、"每日温度"以及"柱状图中最大的矩形"这五道高频面试题，重点探讨如何利用辅助栈维护状态以及利用单调栈解决"下一个更大元素"类问题，帮助读者掌握栈的通用解题思维。

20. 有效的括号

问题描述

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

• 左括号必须用相同类型的右括号闭合。
• 左括号必须以正确的顺序闭合。
• 每个右括号都有一个对应的相同类型的左括号。

示例：

示例 1：
输入：s = "()"
输出：true

示例 2：
输入：s = "()[]{}"
输出：true

示例 3：
输入：s = "(]"
输出：false

标签提示： 栈、字符串

解题思想

利用栈的"后进先出"思想去进行括号的匹配，因为当前遇到的右括号一定是与离他最近的同类型的左括号进行配对的。

具体的处理逻辑可以概括为"消消乐"模式：我们在遍历字符串时，维护一个栈来存储"等待被匹配的左括号"。遇到左括号就入栈，遇到右括号就去栈顶看看能不能配对成功。如果能，就消除（出栈）；如果栈是空的或者配对失败，说明整个序列无效。

解题步骤

1. 预处理（剪枝）：

   由于有效的括号必须成对出现，如果字符串长度为奇数，直接判定为无效并返回 false。

2. 构建映射：

   使用 HashMap 存储"右括号 -> 左括号"的对应关系。这样可以方便地通过右括号快速找到其要求的左括号类型。

3. 遍历与栈操作：

   利用栈的"后进先出"特性进行匹配：

   • 遇到左括号：直接压入栈中，等待后续匹配。

   • 遇到右括号：检查栈顶元素。如果栈为空（没有左括号可供匹配）或者栈顶不等于对应的左括号，直接返回 false；否则，将栈顶元素弹出（匹配成功）。

4. 最终判定：

   遍历结束后，检查栈是否为空。若栈为空，说明所有左括号都找到了匹配项，返回 true；否则说明有多余的左括号，返回 false。

实现代码

class Solution {
    public boolean isValid(String s) {
        int n = s.length();
        if(n % 2 == 1){
            return false;
        }
        Map<Character, Character> map = new HashMap<>();
        map.put(')', '(');
        map.put('}', '{');
        map.put(']', '[');
        Deque<Character> stc = new LinkedList<>();
        for(int i = 0; i < n; i ++){
            char ch = s.charAt(i);
            if(map.containsKey(ch)){
                if(stc.isEmpty() || stc.peek() != map.get(ch)){
                    return false;
                }
                stc.pop();
            }else{
                stc.push(ch);
            }
        }
        return stc.isEmpty();
    }
}

复杂度分析

• 时间复杂度：O(n)。

  我们只需要遍历一次字符串，其中每个字符的入栈和出栈操作都是 O(1) 的。虽然使用了 HashMap，但哈希表的查找操作在平均情况下也可以视为 O(1)。

• 空间复杂度：O(n)。

  在最坏的情况下，例如字符串全是左括号 "((({"，栈的大小会增长到与字符串长度 n 相同。HashMap 的大小是固定的（3个键值对），不影响空间复杂度的量级。

155. 最小栈

问题描述

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例：

示例 1:
输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出：
[null,null,null,null,-3,null,0,-2]
解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

标签提示： 栈、设计

解题思想

栈的 pop() 操作会将栈顶元素移除，如果这个元素恰好是当前的最小值，那么移除后我们如何快速知道剩下的元素里谁是新的最小值？

解决这个问题的核心思想是使用辅助栈。我们维护一个与主栈"同步"的辅助栈，其中存储着当前位置对应的历史最小值。也就是说，辅助栈的栈顶永远代表着当前主栈中所有元素的最小值。通过空间换时间，将获取最小值的时间复杂度降为 O(1)。

解题步骤

1. 初始化双栈：
   定义主栈 stc 用于存储数据，辅助栈 minValue 用于存储同步的最小值。
2. 防空处理：
   初始化 minValue 时，预先压入一个极大值（Integer.MAX_VALUE）。这一步的目的是为了让后续的 push 和 pop 操作无需判断栈是否为空，直接比较或弹出即可，简化代码逻辑。
3. 同步入栈 (push)：
   每次压入元素时，主栈直接压入该值；辅助栈则压入 min(当前值, 辅助栈栈顶)。这样保证了辅助栈的每个位置都记录了"截至当前层"的全局最小值。
4. 同步出栈 (pop)：
   每次弹出元素时，同时对主栈和辅助栈执行弹出操作。由于两个栈是完全同步变化的，辅助栈新的栈顶自然就是剩余元素的最小值。
5. 获取结果：
   top() 直接看主栈栈顶，getMin() 直接看辅助栈栈顶。

实现代码

class MinStack {
    // 用辅助栈来实现，利用一个最小值栈，同步插入当前最小值，出也同步出
    // 比如当前最小值为x，那么只有插入比x小的才会更新最小值，否则都为x
    Deque<Integer> stc;
    Deque<Integer> minValue;    // 最小值栈（对应元素）
    public MinStack() {
        stc = new LinkedList<Integer>();
        minValue = new LinkedList<Integer>();
        minValue.push(Integer.MAX_VALUE);    // 初始化插入一个最大值
    }
    
    public void push(int val) {
        stc.push(val);
        minValue.push(Math.min(val, minValue.peek()));
    }
    
    public void pop() {
        stc.pop();
        minValue.pop();
    }
    
    public int top() {
        return stc.peek();
    }
    
    public int getMin() {
        return minValue.peek();
    }
}

复杂度分析

• 时间复杂度：O(1)。
  对于 push、pop、top 和 getMin 操作，我们都只涉及栈顶的常量级操作（比较、压入、弹出），没有循环遍历。
• 空间复杂度：O(N)。
  最坏情况下（例如递减序列），辅助栈需要存储与主栈同样数量的元素，因此需要 N 的额外空间。

394. 字符串解码

问题描述

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数 k ，例如不会出现像 3a 或 2[4] 的输入。

测试用例保证输出的长度不会超过 10^5。

示例：

示例 1：
输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：
输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：
输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

标签提示： 栈、递归、字符串

解题思想

这道题的核心难点在于处理嵌套结构（如 3[a2[c]]），以及数字可能是多位数的情况。

这里使用了双栈的策略来模拟"层级递归"的过程：

• 数字栈：存储当前的重复倍率（k）。
• 字符串栈：存储进入当前嵌套层级之前已经构建好的字符串（类似于函数调用的上下文保存）。

当遇到 [ 时，表示进入下一层，我们将当前的状态"压栈"暂存并重置；当遇到 ] 时，表示当前层处理完毕，我们"出栈"恢复上一层的状态，并将当前层解码后的字符串拼接到上一层中。

解题步骤

1. 初始化工具：

   建立一个数字栈 numStc 和一个字符串栈 strStc，以及一个 StringBuilder (currStr) 用于记录当前正在处理的层级的字符串。

2. 遍历字符：

   逐个扫描字符串中的字符，分四种情况处理：

   • 遇到数字：计算连续的数字值（处理如 10、100 这种多位数）。
   • 遇到 [：表示进入新的嵌套层级。将当前的倍率 k 和当前字符串 currStr 分别压入对应的栈中保存（保存现场），然后重置 k = 0
     和 currStr 为空，准备处理内层。
   • 遇到 ]：表示当前层级结束。从数字栈弹出倍率 num，从字符串栈弹出上一层的字符串 preStr。将当前层处理好的 currStr 重复
     num 次，然后拼接到 preStr 后面，并将结果赋值给 currStr（恢复现场并合并结果）。
   • 遇到字母：直接追加到当前的 currStr 中。

3. 返回结果：

   遍历结束后，currStr 中存储的就是完全解码后的字符串，直接返回。

实现代码

class Solution {
    // 利用栈，用于存储遇到的数字，然后读左括号接下的字母，然后遇到右括号，弹出数字，将当前字符串以该数字次数加入结果字符串中（栈为空的时候）
    // 但是目前难于解决嵌套问题；那么还需要一个栈用于存储前面层次的字符串
    public String decodeString(String s) {
        Deque<Integer> numStc = new LinkedList<Integer>();  // 数字栈
        Deque<StringBuilder> strStc = new LinkedList<StringBuilder>();  // 层级字符串栈
        StringBuilder currStr = new StringBuilder();
        int k = 0;  // 用于计算多位数字
        for(char ch : s.toCharArray()){
            if(Character.isDigit(ch)){  // 是数字的情况
                // 处理多位数,连续出现
                k = k * 10 + (ch - '0');
            }else if(ch == '['){    // 左括号的情况,数字入栈，当前层级字符串入栈
                numStc.push(k);
                strStc.push(currStr);
                // 重置现场
                k = 0;
                currStr = new StringBuilder();
            }else if(ch == ']'){    // 右括号的情况，当前层次字符串加入上一层级（根据出栈数字次数）
                // 构建新字符串
                int num = numStc.pop();
                StringBuilder preStr = strStc.pop();
                String repeatStr = currStr.toString().repeat(num);
                currStr = new StringBuilder(preStr.toString() + repeatStr);
            }else{  // 直接是字母情况，之前添加到当前字符串
                currStr.append(ch);
            }
        }
        return currStr.toString();
    }
}

复杂度分析

• 时间复杂度：O(N)。

  这里的 N 指的是解码后字符串的长度。虽然我们只遍历了一遍输入字符串，但在 ] 的操作中涉及到字符串的拼接与复制，其总操作次数与最终生成的字符串长度成正比。

• 空间复杂度：O(N)。

  最坏情况下（例如嵌套极深），栈中存储的中间字符串以及辅助空间的总长度与解码后的字符串长度成线性关系。

739. 每日温度

问题描述

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例：

示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]

标签提示： 单调栈、数组

解题思想

这道题最适合使用单调栈来解决。问题本质是寻找"当前元素右边第一个比它大的元素"。

其核心思想是维护一个单调递减的栈（存储数组下标）：

• 栈中存储的是还没有找到更高温度的日期索引。
• 栈内的温度从栈底到栈顶是依次递减的（或者说栈顶元素代表的温度总是最低的）。
• 当我们遍历到一个新的温度时，如果它比栈顶的温度高，说明它就是栈顶日期的"下一个更高温度"。此时我们将栈顶弹出，计算日期差；重复这个过程，直到栈为空或当前温度不再比栈顶高，最后将当前索引入栈。

解题步骤

1. 初始化数据结构：
   创建一个栈 stc 用于存储日期索引，以及一个长度为 n 的结果数组 ans（默认初始化为 0）。
2. 正向遍历温度数组：
   从左到右依次检查每一天的温度。
3. 维护单调性与计算结果：
   对于当前温度 temperatures[i]，检查栈是否为空以及当前温度是否高于栈顶索引所代表的温度：
   • 如果是：说明找到了栈顶日期的升温日。弹出栈顶索引 id，计算天数差 i - id 并赋值给 ans[id]。
   • 循环执行上述操作，直到栈为空或当前温度不再高于栈顶温度。
4. 入栈：
   将当前日期的索引 i 压入栈中，等待后续可能的更高温来匹配。
5. 返回结果：
   遍历结束后，数组 ans 中存储的就是每一天需要等待的天数（栈中剩余的索引对应的值保持为 0，表示之后没有更高温）。

实现代码

class Solution {
    // 利用栈，此题关键是栈中存储什么？
    // 栈里保持单调性（单调栈），比如温度入栈，那么就将栈中比他小的出栈
    // 要得出距离（天数），那么入栈的是天数的索引（数组下标）
    public int[] dailyTemperatures(int[] temperatures) {
        int n = temperatures.length;
        Deque<Integer> stc = new LinkedList<>();
        int[] ans = new int[n];
        for(int i = 0; i < n; i ++){
            // 出栈,并计算结果
            while(!stc.isEmpty() && temperatures[i] > temperatures[stc.peek()]){
                int id = stc.pop();
                ans[id] = i - id;
            }
            stc.push(i);
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：O(N)。
  虽然代码中包含 while 循环，但每个元素（索引）最多被压入栈一次，也最多被弹出栈一次。因此总的操作次数是线性的。
• 空间复杂度：O(N)。
  最坏情况下，温度是递减的（例如 [5, 4, 3, 2, 1]），栈会将所有元素都存入，空间占用为 N。

84. 柱状图中最大的矩形

问题描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例：

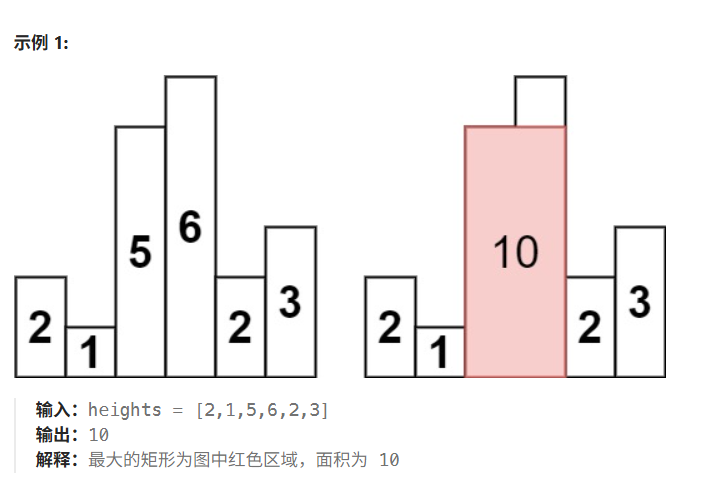
标签提示： 单调栈、数组

解题思想

这道题的核心思想是利用单调栈来寻找柱子左边和右边第一个比它小的柱子，从而确定以该柱子高度为矩形的最大宽度。

矩形的高度由"最短的柱子"决定。当我们维护一个单调递增的栈（存储索引）时，栈顶元素代表的是局部最高点。一旦遍历到比栈顶高度小的元素，就触发了计算：这意味着栈顶元素的右边界找到了（当前元素），而左边界就是栈顶元素下面的那个元素（即弹出后的新栈顶）。此时，栈顶元素对应的矩形面积就是确定的。

解题步骤

1. 添加哨兵：

   在原数组末尾添加一个高度为 0 的哨兵元素。这样做的目的是为了在遍历结束时，强制将栈中剩余的所有元素依次弹出计算，从而避免在循环结束后单独写逻辑处理剩余栈。

2. 初始化栈：

   创建一个栈 stc，用于存储柱子的索引，且栈内对应的高度保持单调递增。

3. 遍历与出栈计算：

   遍历扩展后的数组：

   当前高度 < 栈顶高度：说明找到了栈顶柱子的右边界（当前索引 i）。

   • 弹出栈顶索引，记为 mid，高度为 h = heights[mid]。
   • 确定左边界：如果栈不为空，左边界为当前栈顶索引 stc.peek()；如果栈为空，说明 mid 是目前最小的，左边界视为 -1。
   • 计算宽度：width = i - left - 1（即左右边界之间的距离）。
   • 计算面积并更新最大值。

   当前高度 >= 栈顶高度：直接将当前索引入栈。

4. 返回结果：

   遍历结束后，记录的最大面积即为答案

实现代码

class Solution {
    // 跨柱形成的最大矩形的高度是由矮的那个决定
    // 得使用单调栈的去解决这个问题，遇到比栈顶大的元素进栈，小的则出栈，计算面积
    // 栈用于存储高度的下标，用于计算矩形的宽度
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        // 添加哨兵，处理边界问题
        int[] newHeights = new int[n + 1];
        for(int i = 0; i < n; i ++){
            newHeights[i] = heights[i];
        }
        newHeights[n] = 0;
        // 单调栈，存储柱子的索引
        Deque<Integer> stc = new LinkedList<>();
        int maxArea = 0;
        for(int i = 0; i < n + 1; i ++){
            // 当前柱子比栈顶矮，右边界出现了，也就是当前栈顶，且为矩形高
            while(!stc.isEmpty() && newHeights[i] < newHeights[stc.peek()]){
                int height = newHeights[stc.pop()];
                // 计算宽度，找左边界
                int width;
                if(!stc.isEmpty()){
                    width = i - 1 - stc.peek();
                }else{
                    // 栈为空，那么左边界为0开始
                    width = i;
                }
                // 计算并更新面积
                maxArea = Math.max(maxArea, height * width);
            }
            // 当前柱子进栈（进栈前便处理成单调栈（维持特性））
            stc.push(i);
        }
        return maxArea;
    }
}

复杂度分析

• 时间复杂度：O(N)。
  虽然代码中看起来有双重循环，但每个元素最多被压入栈一次，也最多被弹出栈一次。
• 空间复杂度：O(N)。
  最坏情况下（例如递增序列），栈的大小会达到 N。此外新建的辅助数组也是 O(N) 空间。

个人学习总结

通过对这五道经典栈题目的系统练习，我深刻体会到了栈"后进先出"特性在算法设计中的巧妙应用，主要收获如下：
基础匹配逻辑： 利用栈处理成对出现的符号（如括号），通过"遇左进，遇右消"的思路，能轻松解决匹配与校验问题。
辅助栈思维： 当需要在动态操作中快速获取状态极值（如最小栈）时，利用辅助栈同步记录历史状态，是典型的"空间换时间"策略，能将查询复杂度降至 O(1)。
模拟递归层级： 对于嵌套结构（如字符串解码），利用双栈分别存储"倍率"和"前缀字符串"，能够非递归地实现层级回溯与拼接，逻辑更加清晰且不易出错。
单调栈的威力： 这是本次学习的核心。无论是"每日温度"的寻找下一个更高温（单调递减栈），还是"柱状图中最大的矩形"的确定左右边界（单调递增栈），其本质都是通过维护栈的有序性，在 O(N) 时间内找到元素的左/右边界。掌握这种"以空间换时间，维护单调性确定边界"的模板思维，是解决此类区间最值问题的金钥匙。