算法刷题--链表

文章目录

- [1、203 移除链表元素](#1、203 移除链表元素)
- - 法二：虚拟头结点法
  - 为什么这段代码更好？
  - [1. 代码逐行直译](#1. 代码逐行直译)
  - [2. 为什么要这么做？（核心痛点）](#2. 为什么要这么做？（核心痛点）)
  - [3. 内存与指针的直观图示](#3. 内存与指针的直观图示)
  - [4. 这种写法的"高级感"体现在哪？](#4. 这种写法的“高级感”体现在哪？)
  - 延伸思考
  - [法三递归](#法三递归)
  - [1. 递归代码实现](#1. 递归代码实现)
  - [2. 递归过程的直观理解](#2. 递归过程的直观理解)
  - [3. 递归法的优缺点](#3. 递归法的优缺点)
  - [4. 总结与建议](#4. 总结与建议)
- [2、707 设计链表](#2、707 设计链表)
- - [1. 数据结构定义](#1. 数据结构定义)
  - [2. 五大核心操作的解题思路](#2. 五大核心操作的解题思路)
  - - [① 获取节点 `get(index)`](#① 获取节点 get(index))
    - [② 头部插入 `addAtHead(val)`](#② 头部插入 addAtHead(val))
    - [③ 尾部插入 `addAtTail(val)`](#③ 尾部插入 addAtTail(val))
    - [④ 按索引插入 `addAtIndex(index, val)`](#④ 按索引插入 addAtIndex(index, val))
    - [⑤ 按索引删除 `deleteAtIndex(index)`](#⑤ 按索引删除 deleteAtIndex(index))
  - [3. 为什么一定要用虚拟头节点？](#3. 为什么一定要用虚拟头节点？)
  - [4. 常见坑点（避坑指南）](#4. 常见坑点（避坑指南）)
  - [5. 进阶：单链表还是双链表？](#5. 进阶：单链表还是双链表？)
- [3、206 翻转链表](#3、206 翻转链表)
- - [1. 终止条件（Base Case）](#1. 终止条件（Base Case）)
  - [2. 递归下钻（Pushing down）](#2. 递归下钻（Pushing down）)
  - [3. 指针逆转逻辑（The Magic Step）](#3. 指针逆转逻辑（The Magic Step）)
  - - [举个例子：假设链表是 `1 -> 2 -> 3 -> NULL`](#举个例子：假设链表是 1 -> 2 -> 3 -> NULL)
  - [4. 为什么要设置 `head->next = NULL`？](#4. 为什么要设置 head->next = NULL？)
  - [5. 复杂度分析](#5. 复杂度分析)
- 4、反转链表二
- [5、25 k个一组翻转链表](#5、25 k个一组翻转链表)
- [6、24 两两交换链表中的节点](#6、24 两两交换链表中的节点)
- - [1. 核心变量的作用](#1. 核心变量的作用)
  - [2. 交换逻辑图解（关键 3 步）](#2. 交换逻辑图解（关键 3 步）)
  - [3. 指针迭代更新](#3. 指针迭代更新)
  - [4. 循环条件分析](#4. 循环条件分析)
- [7、 19 删除链表的倒数第N个结点](#7、 19 删除链表的倒数第N个结点)
- [8、07 链表相交](#8、07 链表相交)
- [9、142 环形链表 ②](#9、142 环形链表 ②)
- [时间复杂度：O(n) 空间复杂度：O(1) 核心思想bygimini](#时间复杂度：O(n) 空间复杂度：O(1) 核心思想bygimini)
- - [Floyd 判圈算法两步走](#Floyd 判圈算法两步走)
  - - 第一步：找相遇点
    - 第二步：找入环点
  - 关键点详解
- [10、876 链表的中间节点](#10、876 链表的中间节点)
- [11、141 环形链表](#11、141 环形链表)
- [12、143 重排链表](#12、143 重排链表)

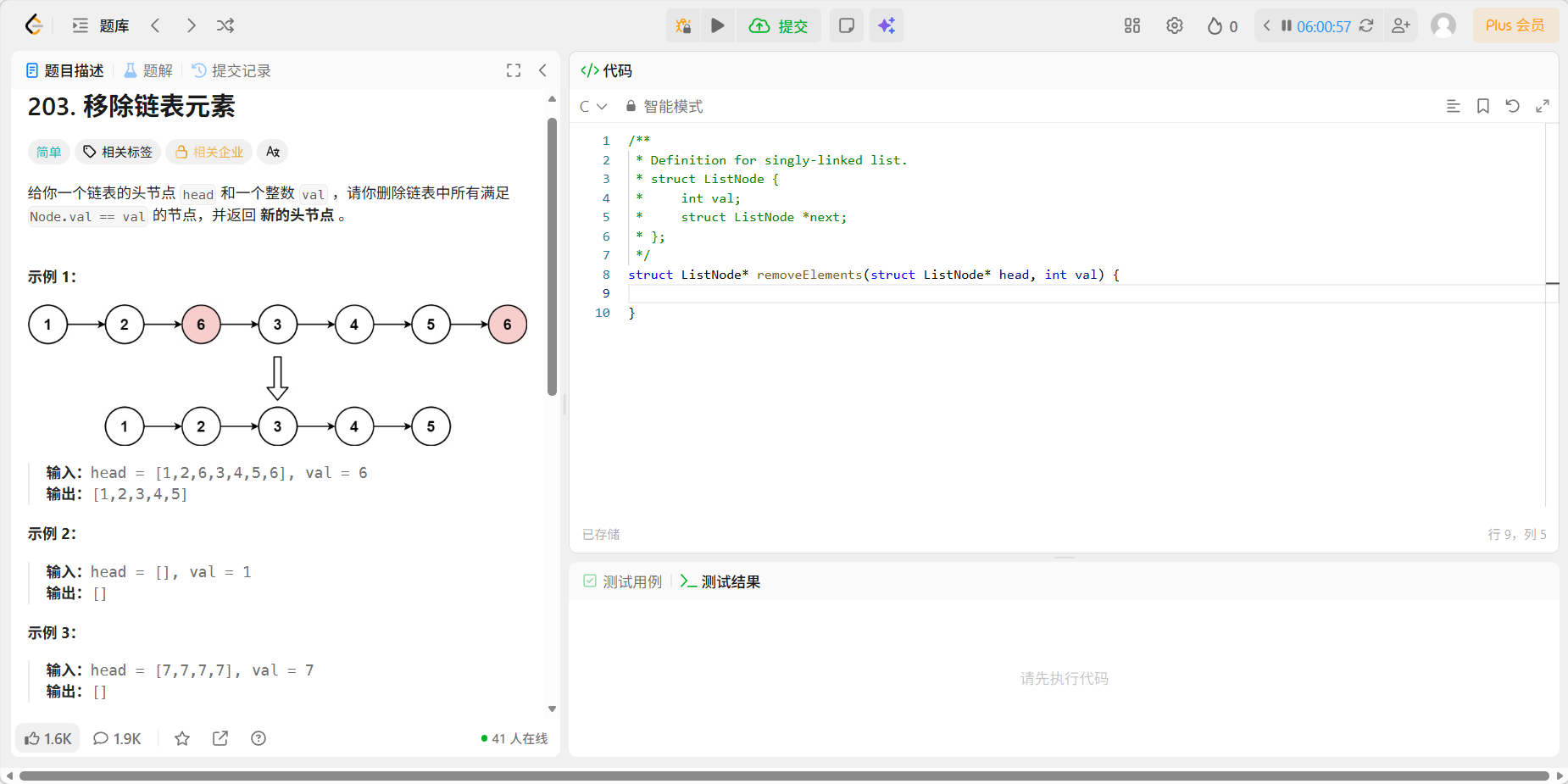
1、203 移除链表元素

题目

代码

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* removeElements(struct ListNode* head, int val) {
    while(head != NULL && head->val == val){
        struct ListNode* tmp = head;
        head = head->next;
        free(tmp);
    }
    if(head == NULL){
        return NULL;
    }
    struct ListNode* p = head;
    while(p->next != NULL){
        if(p->next->val == val){
            struct ListNode* tmp = p->next;
            p->next = p->next->next;
            free(tmp);
        }else{
            p = p->next;
        }
    }
    return head;
}

解题思路:

处理开头的连续删除：如果头节点的值等于 val，需要不断将 head 后移，直到 head 为空或者 head 的值不再等于 val 为止。
处理中间节点：此时 head 已经确定是不需要删除的节点，我们可以安全地使用一个前驱指针 p 从 head 开始向后遍历，检查并删除其后的节点。

时间复杂度：O(n)

空间复杂度：O(1)

法二：虚拟头结点法

通过在头节点前临时增加一个"假节点"，可以把头节点的删除逻辑和普通节点完全统一。

c 复制代码

struct ListNode* removeElements(struct ListNode* head, int val) {
    // 1. 创建虚拟头节点
    struct ListNode dummy;
    dummy.next = head;
    struct ListNode* p = &dummy; // p 始终指向待检查节点的前驱
    
    while (p->next != NULL) {
        if (p->next->val == val) {
            // 2. 发现匹配，删除 p->next
            struct ListNode* tmp = p->next;
            p->next = p->next->next;
            free(tmp); // 释放内存
        } else {
            // 3. 不匹配，前驱指针后移
            p = p->next;
        }
    }
    
    return dummy.next;
}

为什么这段代码更好？

处理了空链表 ：如果 head 是 NULL，p->next 为空，直接退出循环，返回 NULL。
处理了头节点 ：由于 p 从虚拟头节点开始，p->next 第一次检查的就是真正的头节点。
内存安全 ：显式使用 tmp 指针配合 free，避免了野指针问题。

掌握了"虚拟头节点"，你就掌握了链表题的一半技巧！

struct ListNode dummy;
dummy.next = head;
struct ListNode* p = &dummy;
return dummy.next;详细解释这段代码

在链表算法中，这几行代码展示了**"虚拟头节点"（Dummy Node / Sentinel Node）**这一技巧的精髓。它是解决链表问题、尤其是涉及"删除"或"插入"操作时的"银弹"。

以下是深度拆解：

1. 代码逐行直译

struct ListNode dummy;
在栈上开辟了一个真实的 ListNode 结构体变量。
注意：它不是指针，而是一个实际存在的节点。它的 val 字段通常不被初始化（或者初始为 0），因为我们根本不关心它的值。
dummy.next = head;
将这个虚拟节点的 next 指向真正的链表头 head。
形象理解：在原链表的排头兵前面，强行安插了一个" 0 号员工"。
struct ListNode* p = &dummy;
定义一个游标指针 p，指向这个虚拟头节点。
在后续逻辑中，p 通常用来代表"当前检查节点的前驱（上一个节点）"。
return dummy.next;
最后返回时，不返回 head，而返回 dummy.next。
核心作用 ：如果原头节点被删除了，dummy.next 会指向新的头节点；如果原头节点没动，它依然指向原头节点。

2. 为什么要这么做？（核心痛点）

如果不使用虚拟头节点，链表操作会面临两个尴尬的"特殊情况"：

头节点的特殊性：

删除普通节点：需要找到它的前驱节点 prev，执行 prev->next = prev->next->next。
删除头节点：它没有前驱节点！你必须写死一个 if(head->val == val) { head = head->next; }。

空链表的崩溃风险：

很多操作在处理 head->next 时，如果 head 为空会直接段错误。

有了 dummy 之后：

众生平等 ：所有的节点（包括原头节点）现在都有了前驱节点（原头节点的前驱就是 dummy）。
逻辑统一：你可以用同一套代码逻辑处理链表中的任何一个位置，不再需要为"是不是第一个节点"写特判代码。

3. 内存与指针的直观图示

假设链表为 [1] -> [2]，我们要删除 1：

初始状态：

text 复制代码

[dummy] -> [1] -> [2] -> NULL
  ↑         ↑
  p        head

执行删除逻辑（假设 val 为 1）：
p->next 指向的节点值是 1，执行 p->next = p->next->next;：

text 复制代码

[dummy] ---------> [2] -> NULL
  ↑                 ↑
  p            (dummy.next)

最后返回 dummy.next：

你成功拿到了 [2] -> NULL，而不需要管原先的 head 丢到了哪里。

4. 这种写法的"高级感"体现在哪？

安全性 ：dummy 是在栈上定义的（struct ListNode dummy），函数结束时自动销毁，不需要手动 free(dummy)（除非你是用 malloc 申请的虚拟头节点）。
简洁性：它让原本可能需要 20 行的代码缩减到 10 行以内，且 Bug 率大大降低。

延伸思考

在 C 语言中，如果你写的是 struct ListNode* dummy = malloc(sizeof(struct ListNode));，那么在 return 之前一定要先 struct ListNode* newHead = dummy->next; free(dummy); return newHead;。

而你给出的这种 struct ListNode dummy; 写法利用了局部变量的特性，是最推荐、最省心的写法！

法三递归

使用递归来处理链表删除问题，思路会变得非常简洁，甚至可以用"优雅"来形容。递归的核心思想是："我处理好当前这个节点，剩下的交给下一层函数去处理。"

对于 removeElements 这个问题，递归的逻辑可以拆解为：

递归出口（终止条件） ：如果链表为空，直接返回 NULL。
递归单元 ：先让递归函数处理 head->next 之后的所有节点。
当前决策：

如果当前 head 的值等于 val，说明当前节点要被删掉，我们应该返回它后面已经处理好的链表。
如果当前 head 的值不等于 val，说明当前节点要保留，我们将它的 next 指向后面处理好的链表，并返回自己。

1. 递归代码实现

c 复制代码

struct ListNode* removeElements(struct ListNode* head, int val) {
    // 1. 终止条件：如果链表走到了尽头，直接返回
    if (head == NULL) {
        return NULL;
    }

    // 2. 递归：先去处理当前节点后面的链表
    // 我们可以理解为：head->next 后面这一串已经由"递归小助手"帮我们删完多余元素了
    head->next = removeElements(head->next, val);

    // 3. 核心判断：处理当前这个 head
    if (head->val == val) {
        // 如果当前节点需要删除
        struct ListNode* nextNode = head->next;
        // 注意：在 LeetCode 环境中，这里可以直接返回 nextNode
        // 但在严谨的 C 开发中，建议先 free(head) 释放内存
        free(head); 
        return nextNode;
    } else {
        // 如果当前节点不需要删除，直接返回当前 head
        return head;
    }
}

2. 递归过程的直观理解

假设链表是 1 -> 2 -> 6 -> 3，我们要删除 6。

第一步 ：函数一路"向下"钻，直到碰到 NULL。
第二步：从后往前"向上"归：
处理 3：3 != 6，保留，返回 3。
处理 6：6 == 6，删除自己，把后面处理好的 3 返回给上一层。
处理 2：2 != 6，保留，把它的 next 指向返回回来的 3。
处理 1：1 != 6，保留，把它的 next 指向返回回来的 2。
结果：返回 1 -> 2 -> 3。

3. 递归法的优缺点

优点：

极其简洁 ：不需要虚拟头节点，不需要处理复杂的 p 和 p->next 逻辑。
逻辑统一：头节点的删除逻辑自然地包含在递归判断中。

缺点：

空间开销（栈溢出风险） ：递归每一层都会在内存栈中占用空间。如果链表非常长（例如有 10 万个节点），可能会导致栈溢出（Stack Overflow）。
性能：由于频繁的函数调用，速度通常比循环迭代法慢一点。

4. 总结与建议

刷题面试：如果面试官要求写出最简洁的代码，递归是个亮点。
工业环境：在处理可能超长的链表时，**循环迭代法（配合虚拟头节点）**依然是最稳健、最专业的选择。

递归的精髓在于"相信你的函数"------相信 removeElements(head->next, val) 已经帮你把后面的杂事做好了。

2、707 设计链表

题目

"设计链表" (Design Linked List) 是练好链表基本功的"天花板"题目。它不要求你解决某个具体的算法问题，而是要求你完整实现一个功能健全的链表类。

要写好这道题，最关键的思路是：引入"虚拟头节点" (Dummy Head) 并维护一个 size 变量。

1. 数据结构定义

首先，你需要定义链表的节点结构体，以及管理整个链表的控制结构。

c 复制代码

typedef struct MyLinkedList {
    int val;
    struct MyLinkedList* next;
} MyLinkedList;

// 建议：定义一个"控制头"，包含 size 信息
typedef struct {
    int size;
    MyLinkedList* dummyHead;
} MyLinkedListControl;

2. 五大核心操作的解题思路

① 获取节点 `get(index)`

思路：先判断 index 是否合法（）。
操作：从 dummyHead->next 开始，移动 index 次指针即可到达目标节点。
注意：如果 index 无效，直接返回 -1。

② 头部插入 `addAtHead(val)`

思路：直接调用"在第 0 个位置插入"的逻辑，或者手动操作。
操作：新建节点 new new->next = dummyHead->next dummyHead->next = new。不要忘记 size++。

③ 尾部插入 `addAtTail(val)`

思路：直接调用"在第 size 个位置插入"。
操作：遍历到链表的最后一个节点（其 next == NULL），然后接上新节点。

④ 按索引插入 `addAtIndex(index, val)`

思路：
如果 index > size，不插入。
如果 index <= 0，等同于头部插入。
关键点 ：要插入到第 index 个节点，你必须找到它的前驱节点 （即第 index-1 个节点）。
操作：从 dummyHead 开始移动 index 次，找到前驱节点 prev。

⑤ 按索引删除 `deleteAtIndex(index)`

思路：判断 index 是否合法（）。
操作：同样需要找到目标节点的前驱节点 prev。
逻辑：tmp = prev->next prev->next = prev->next->next free(tmp)。不要忘记 size--。

3. 为什么一定要用虚拟头节点？

如果不使用虚拟头节点，你在 addAtHead 和 deleteAtIndex(0) 时，必须修改 head 指针本身的值。这会导致代码中充斥着大量的 if (index == 0) 特判。
使用虚拟头节点后，所有位置的操作（包括头部）都统一成了"找到前驱节点，修改其 next 指向"。

4. 常见坑点（避坑指南）

索引越界 ：在 get 和 delete 时，index 必须小于 size；但在 add 时，index 可以等于 size（相当于尾插）。
内存释放 ：deleteAtIndex 必须 free 掉被删除的节点，否则会内存泄漏。
Size 维护 ：每增加一个节点 size++，每删除一个节点 size--。
循环边界：

找第 index 个节点的前驱：从 dummyHead 开始，走 index 步。
示例：index=0 时，走 0 步，正好停在 dummyHead。

5. 进阶：单链表还是双链表？

这道题题目没规定。

单链表：实现简单，节省内存。
双链表 ：删除和插入（尤其是尾部）效率更高，但逻辑复杂，需要维护 prev 指针。如果是初练，建议先攻克单链表+虚拟头节点的写法。

代码

单链表

c 复制代码

#include <stdlib.h>
#include <stdio.h>

// 1. 定义链表节点结构体
typedef struct MyLinkedList {
    int val;
    struct MyLinkedList* next;
} MyLinkedList;

// 2. 定义链表管理结构体（包含虚拟头节点和长度）
typedef struct {
    int size;
    MyLinkedList* dummyHead;
} MyLinkedListControl;

/** 初始化链表 */
MyLinkedListControl* myLinkedListCreate() {
    MyLinkedListControl* obj = (MyLinkedListControl*)malloc(sizeof(MyLinkedListControl));
    obj->size = 0;
    // 创建虚拟头节点，不存储有效数据
    obj->dummyHead = (MyLinkedList*)malloc(sizeof(MyLinkedList));
    obj->dummyHead->next = NULL;
    return obj;
}

/** 获取第 index 个节点的值 */
int myLinkedListGet(MyLinkedListControl* obj, int index) {
    // 检查索引合法性：index 从 0 开始，不能大于等于 size
    if (index < 0 || index >= obj->size) {
        return -1;
    }
    // 从真正的第一个节点开始（即 dummyHead->next）
    MyLinkedList* cur = obj->dummyHead->next;
    // 移动 index 次指针，到达目标节点
    while (index--) {
        cur = cur->next;
    }
    return cur->val;
}

/** 在头部插入节点 */
void myLinkedListAddAtHead(MyLinkedListControl* obj, int val) {
    MyLinkedList* newNode = (MyLinkedList*)malloc(sizeof(MyLinkedList));
    newNode->val = val;
    // 新节点指向原来的首节点
    newNode->next = obj->dummyHead->next;
    // 虚拟头节点指向新节点
    obj->dummyHead->next = newNode;
    obj->size++;
}

/** 在尾部插入节点 */
void myLinkedListAddAtTail(MyLinkedListControl* obj, int val) {
    MyLinkedList* newNode = (MyLinkedList*)malloc(sizeof(MyLinkedList));
    newNode->val = val;
    newNode->next = NULL;
    
    // 找到当前链表的最后一个节点
    MyLinkedList* cur = obj->dummyHead;
    while (cur->next != NULL) {
        cur = cur->next;
    }
    cur->next = newNode;
    obj->size++;
}

/** 在第 index 个节点前插入节点 */
void myLinkedListAddAtIndex(MyLinkedListControl* obj, int index, int val) {
    // 1. 如果 index 大于链表长度，不插入
    if (index > obj->size) return;
    // 2. 如果 index 小于 0，通常视为在头部插入
    if (index < 0) index = 0;

    // 关键：要插入到第 index 个，必须找到它的前驱节点（即第 index-1 个）
    // 因为有 dummyHead，从 dummyHead 开始走 index 步，正好停在前驱节点上
    MyLinkedList* prev = obj->dummyHead;
    while (index--) {
        prev = prev->next;
    }

    MyLinkedList* newNode = (MyLinkedList*)malloc(sizeof(MyLinkedList));
    newNode->val = val;
    newNode->next = prev->next;
    prev->next = newNode;
    obj->size++;
}

/** 删除第 index 个节点 */
void myLinkedListDeleteAtIndex(MyLinkedListControl* obj, int index) {
    // 检查索引合法性
    if (index < 0 || index >= obj->size) return;

    // 同样需要找到待删除节点的前驱节点
    MyLinkedList* prev = obj->dummyHead;
    while (index--) {
        prev = prev->next;
    }

    // 记录待删除节点，用于 free 释放内存
    MyLinkedList* tmp = prev->next;
    prev->next = prev->next->next;
    free(tmp);
    obj->size--;
}

/** 释放链表内存 */
void myLinkedListFree(MyLinkedListControl* obj) {
    MyLinkedList* cur = obj->dummyHead;
    // 循环释放每一个节点（包括 dummyHead）
    while (cur != NULL) {
        MyLinkedList* tmp = cur;
        cur = cur->next;
        free(tmp);
    }
    // 最后释放管理结构体
    free(obj);
}

下面这版改变了myLinkedListAddAtIndex()函数的位置，然后myLinkedListAddAtHead()和myLinkedListAddAtTail()直接调用myLinkedListAddAtIndex()函数实现在头部和尾部插入节点

c 复制代码

#define MAX(a,b)((a) > (b) ? (a) : (b))

typedef struct {
    struct ListNode *head;
    int size;   
} MyLinkedList;

struct ListNode* ListNodeCreat(int val){
    struct ListNode* node = (struct ListNode*)malloc(sizeof(struct ListNode));
    node->val = val;
    node->next = NULL;
    return node;
}

MyLinkedList* myLinkedListCreate() {
    MyLinkedList* obj = (MyLinkedList*)malloc(sizeof(MyLinkedList));
    obj->head = ListNodeCreat(0);
    obj->size = 0;
    return obj;
}

int myLinkedListGet(MyLinkedList* obj, int index) {
    if(index < 0 || index >= obj->size){
        return -1;
    }
    struct ListNode* cur = obj->head;
    for(int i = 0;i <= index;i++){
        cur = cur->next;
    }
    return cur->val;
}

void myLinkedListAddAtIndex(MyLinkedList* obj,int index,int val){
    if(index > obj->size){
        return;
    }
    index = MAX(0,index);
    obj->size++;
    struct ListNode* pred = obj->head;
    for(int i = 0;i < index;i++){
        pred = pred->next;
    }
    struct ListNode *toAdd = ListNodeCreat(val);
    toAdd->next = pred->next;
    pred->next = toAdd;
}

void myLinkedListAddAtHead(MyLinkedList* obj, int val) {
    myLinkedListAddAtIndex(obj,0,val);
}

void myLinkedListAddAtTail(MyLinkedList* obj, int val) {
    myLinkedListAddAtIndex(obj,obj->size,val);
}

// void myLinkedListAddAtIndex(MyLinkedList* obj, int index, int val) {
    
// }

void myLinkedListDeleteAtIndex(MyLinkedList* obj, int index) {
    if(index < 0 || index >= obj->size){
        return;
    }
    obj->size--;
    struct ListNode *pred = obj->head;
    for(int i = 0;i < index;i++){
        pred = pred->next;
    }
    struct ListNode *p = pred->next;
    pred->next = pred->next->next;
    free(p);
}

void myLinkedListFree(MyLinkedList* obj) {
    struct ListNode* cur = NULL,*tmp = NULL;
    for(cur = obj->head;cur;){
        tmp = cur;
        cur = cur->next;
        free(tmp);
    }
    free(obj);
}

/**
 * Your MyLinkedList struct will be instantiated and called as such:
 * MyLinkedList* obj = myLinkedListCreate();
 * int param_1 = myLinkedListGet(obj, index);
 
 * myLinkedListAddAtHead(obj, val);
 
 * myLinkedListAddAtTail(obj, val);
 
 * myLinkedListAddAtIndex(obj, index, val);
 
 * myLinkedListDeleteAtIndex(obj, index);
 
 * myLinkedListFree(obj);
*/

时间复杂度: 涉及 index 的相关操作为 O(index), 其余为 O(1)

空间复杂度: O(n)

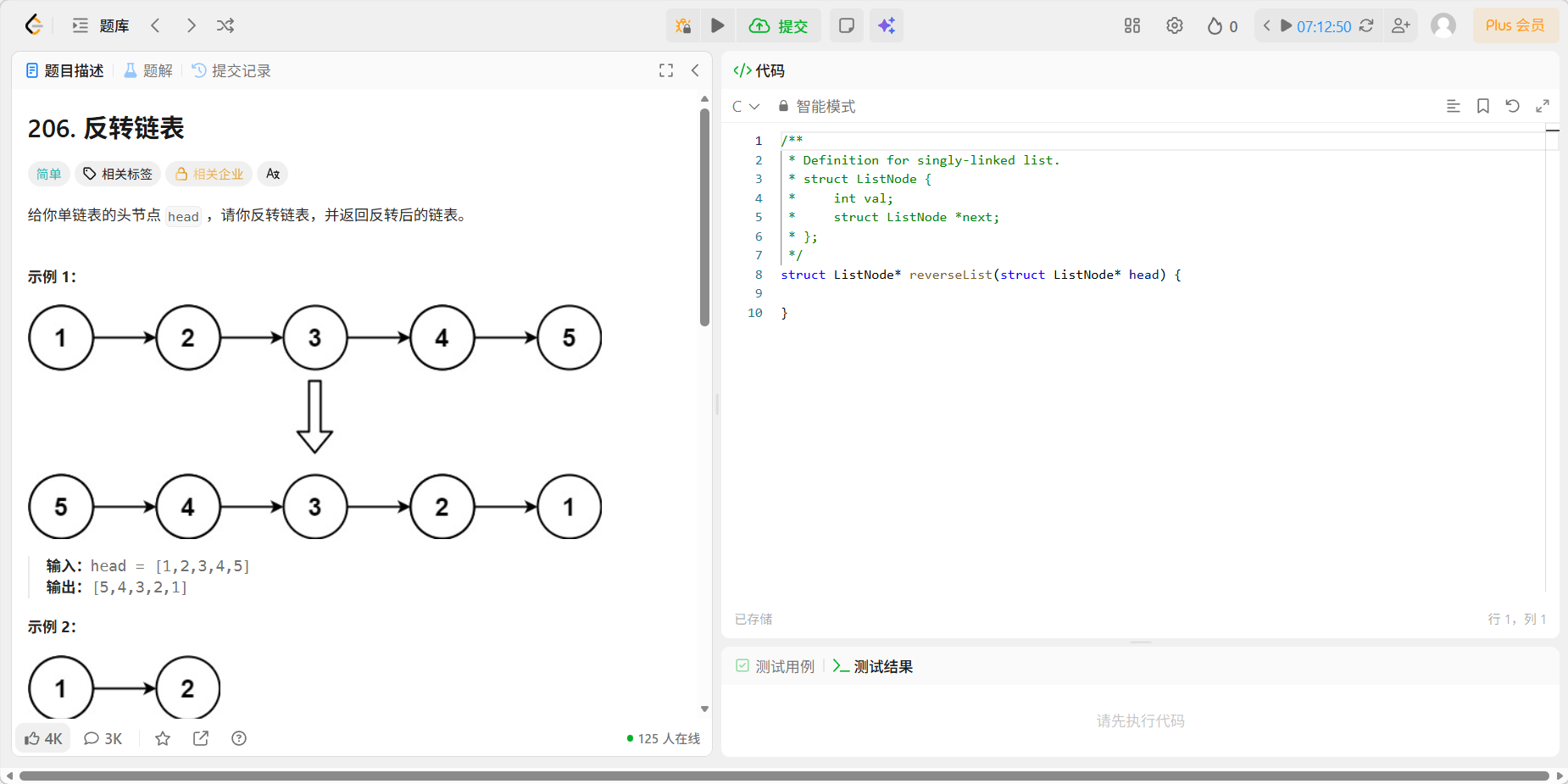
3、206 翻转链表

题目

看了灵神的视频，醍醐灌顶~反转链表

代码

迭代

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* reverseList(struct ListNode* head) {
    if(head == NULL) return NULL;
    if(head ->next == NULL) return head;
    struct ListNode* p = NULL;
    struct ListNode* q = head;
    while(q != NULL){
        struct ListNode* tmp = q->next;
        q->next = p;
        p = q;
        q = tmp;
    }
    return p;
}

迭代的代码还是比较好懂的~

时间复杂度：O(n)

空间复杂度：O(1)

2: 递归

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* reverseList(struct ListNode* head) {
    if(head == NULL || head->next == NULL){
        return head;
    }
    struct ListNode* rev_head = reverseList(head->next);
    struct ListNode* tail = head->next;
    tail->next = head;
    head->next = NULL;

    return rev_head;
}

贴一下详解递归

它的逻辑非常精妙，利用了函数调用栈的"回溯"特性，从链表的末尾开始，逐个改变指针的指向。

我们可以将这段代码拆解为三个核心部分：

1. 终止条件（Base Case）

c 复制代码

if(head == NULL || head->next == NULL){
    return head;
}

作用：当递归到达链表的最后一个节点时，停止下钻。
返回值 ：返回这个最后一个节点，它将成为翻转后新链表的新头节点 （rev_head）。

2. 递归下钻（Pushing down）

c 复制代码

struct ListNode* rev_head = reverseList(head->next);

这一步会一直往后找，直到找到最后一个节点。
关键点 ：在整个回溯过程中，rev_head 始终指向原链表的最后一个节点，并像接力棒一样一层层传回到最外层。

3. 指针逆转逻辑（The Magic Step）

当递归开始"归"（回溯）的时候，每一层都在做下面这件事：

c 复制代码

struct ListNode* tail = head->next; // 找到当前节点的"下一个节点"（翻转后的末尾）
tail->next = head;                  // 让"下一个节点"指向自己（实现反向连接）
head->next = NULL;                  // 断开自己原本指向后面的指针，防止形成环

举个例子：假设链表是 `1 -> 2 -> 3 -> NULL`

递归钻到节点 3，返回 3。此时 rev_head 为 3。
回溯到节点 2 的这一层：

head 是 2，head->next 是 3。
tail 指向 3。
tail->next = head：也就是 3 -> 2。
head->next = NULL：此时链表暂时变成 2 <- 3（2 的后面为空）。

回溯到节点 1 的这一层：

head 是 1，head->next 是 2。
tail 指向 2。
tail->next = head：也就是 2 -> 1。
head->next = NULL：链表最终变成 3 -> 2 -> 1 -> NULL。

4. 为什么要设置 `head->next = NULL`？

这是为了处理原链表的头节点 。

如果不把 head->next 设为 NULL，那么原链表的头节点（翻转后的尾节点）依然会指向它原本的下一个节点，从而导致链表在末尾形成一个环（例如 1 -> 2 变成了 1 <-> 2）。

5. 复杂度分析

时间复杂度：。每个节点都被访问并处理了一次。
空间复杂度 ：。由于是递归，每一层递归都会占用系统栈空间。如果链表极长（如几万个节点），可能会导致栈溢出（Stack Overflow）。

时间复杂度：O(n)

空间复杂度：O(n)

4、反转链表二

题目

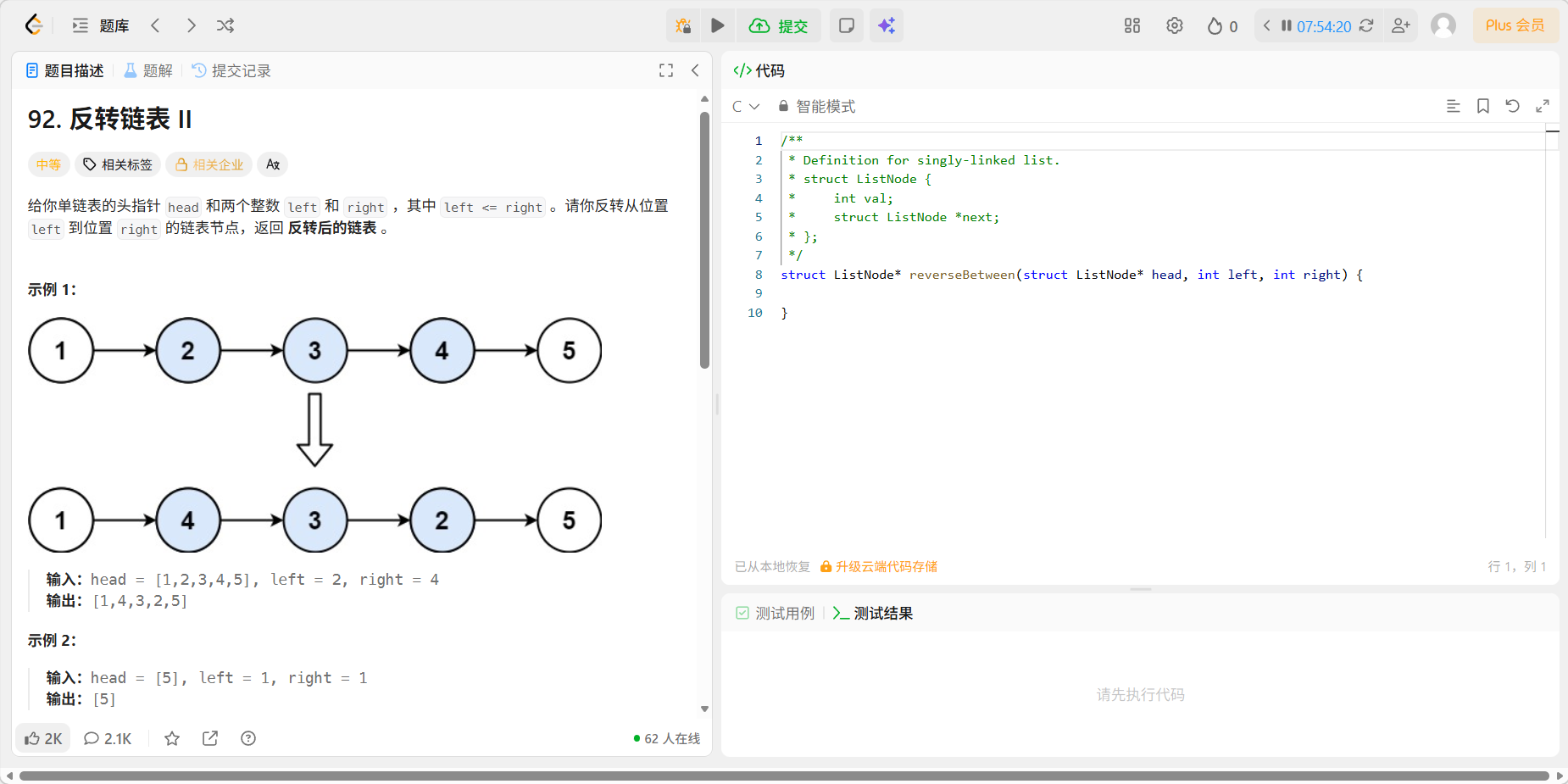
代码

采用了"先切分、再翻转、最后连接"的思路，并且巧妙使用了虚拟头节点（Dummy Node)。

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* reverseBetween(struct ListNode* head, int left, int right) {
    if(head->next == NULL || head == NULL || (right-left)<0){
        return head;
    }
    struct ListNode dummy;
    dummy.next = head;
    struct ListNode* p0 = &dummy;
    for(int i = 0;i < left-1;i++){
        p0 = p0->next;
    }
    struct ListNode* pre = NULL;
    struct ListNode* cur = p0->next;
    for(int i = 0;i < right-left+1;i++){
        struct ListNode* nxt = cur->next;
        cur->next = pre;
        pre = cur;
        cur = nxt;
    }
    p0->next->next = cur;
    p0->next = pre;
    return dummy.next;

}

时间复杂度：O(n)

空间复杂度：O(1)

5、25 k个一组翻转链表

题目

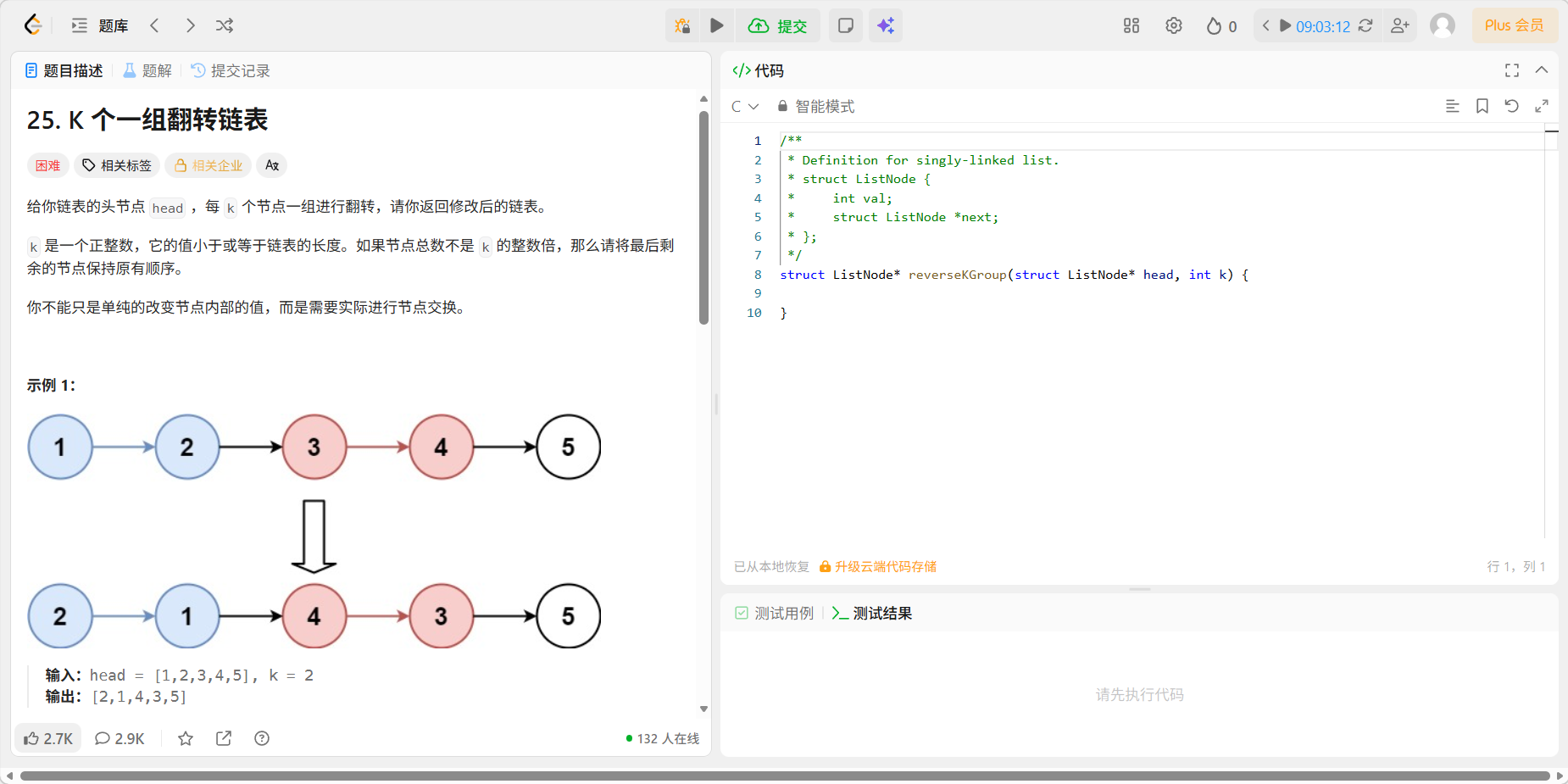
代码

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* reverseKGroup(struct ListNode* head, int k) {
    struct ListNode dummy;
    dummy.next = head;
    struct ListNode* p = &dummy;
    int n = 0;
    while(p->next != NULL){
        p = p->next;
        n++;
    }
    p = &dummy;
    while(n >= k){
        n -= k;
        struct ListNode* pre = NULL;
        struct ListNode* cru = p->next;
        for(int i = 0;i < k;i++){
            struct ListNode* nxt = cru->next;
            cru->next = pre;
            pre = cru;
            cru = nxt;
        }
        struct ListNode* tmp = p->next;
        p->next->next = cru;
        p->next = pre;
        p = tmp;
    }

    return dummy.next;
}

时间复杂度：O(n)

空间复杂度：O(1)

6、24 两两交换链表中的节点

题目

代码

只需要把上题的k改成2即可

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* swapPairs(struct ListNode* head) {
    if(head == NULL || head->next == NULL){
        return head;
    }
    struct ListNode dummy;
    dummy.next = head;
    struct ListNode* p = &dummy;

    int n = 0;
    while(p->next != NULL){
        p = p->next;
        n++;
    }
    p = &dummy;

    while(n >= 2){
        n -= 2;
        struct ListNode* pre = NULL;
        struct ListNode* cur = p->next;
        for(int i = 0;i < 2;i++){
            struct ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        struct ListNode* tmp = p->next;
        p->next->next = cur;
        p->next = pre;
        p = tmp;
    }
    return dummy.next;
}

时间复杂度：O(n)

空间复杂度：O(1)

另解

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* swapPairs(struct ListNode* head) {
    typedef struct ListNode ListNode;
    ListNode *fakehead = (ListNode*)malloc(sizeof(ListNode));
    fakehead->next = head;
    ListNode* right = fakehead->next;
    ListNode* left = fakehead;
    while(left && right && right->next){
        left->next = right->next;
        right->next = left->next->next;
        left->next->next = right;
        left = right;
        right = left->next;
    }
    return fakehead->next;
}

核心思路：利用**虚拟头节点（fakehead）来简化头部交换的逻辑，并使用双指针（left, right）**来控制每一对节点的转向。

1. 核心变量的作用

fakehead ：虚拟头节点。它的 next 始终指向链表的"当前新头"。有了它，我们就不需要单独写 if 来处理第一个和第二个节点的交换。
left：指向"当前要交换的一对节点"的前驱节点（即上一对交换完后的末尾）。
right：指向"当前要交换的一对节点"中的第一个节点。

2. 交换逻辑图解（关键 3 步）

假设链表是 A -> B -> C -> D，我们要交换 B 和 C：

初始状态：left 指向 A，right 指向 B。

**第一步：left->next = right->next;**
让 A 跳过 B，直接指向 C。
此时链表：A -> C；B 还在指向 C。
**第二步：right->next = left->next->next;**
让 B 指向 C 的后面（即 D）。
此时链表：B -> D。
**第三步：left->next->next = right;**
这里的 left->next 就是 C，所以这行意思是让 C -> B。
此时链表完成了交换：A -> C -> B -> D。

3. 指针迭代更新

c 复制代码

left = right;        // 交换后，right 变成了这组的末尾，也就是下一组的前驱
right = left->next;  // right 移动到下一组的第一个节点

交换完成后，指针向后移动，准备处理下一对。

4. 循环条件分析

c 复制代码

while(left && right && right->next)

right: 确保当前这一组有第一个节点。
right->next: 确保当前这一组有第二个节点。如果只剩一个节点，就不满足两两交换，直接停止。

7、 19 删除链表的倒数第N个结点

题目

代码

核心思想：快慢指针，先让快指针先走n步，然后快慢指针同时移动~

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* removeNthFromEnd(struct ListNode* head, int n) {
    struct ListNode dummy;
    dummy.next = head;
    struct ListNode* p = &dummy;
    struct ListNode* q = &dummy;

    for(int i = 0;i < n;i++){
        p = p->next;
    }
    while(p->next != NULL){
        p = p->next;
        q = q->next;
    }
    struct ListNode* tmp = q->next;
    q->next = q->next->next;
    free(tmp);
    return dummy.next;
}

时间复杂度：O(n)

空间复杂度：O(1)

8、07 链表相交

题目

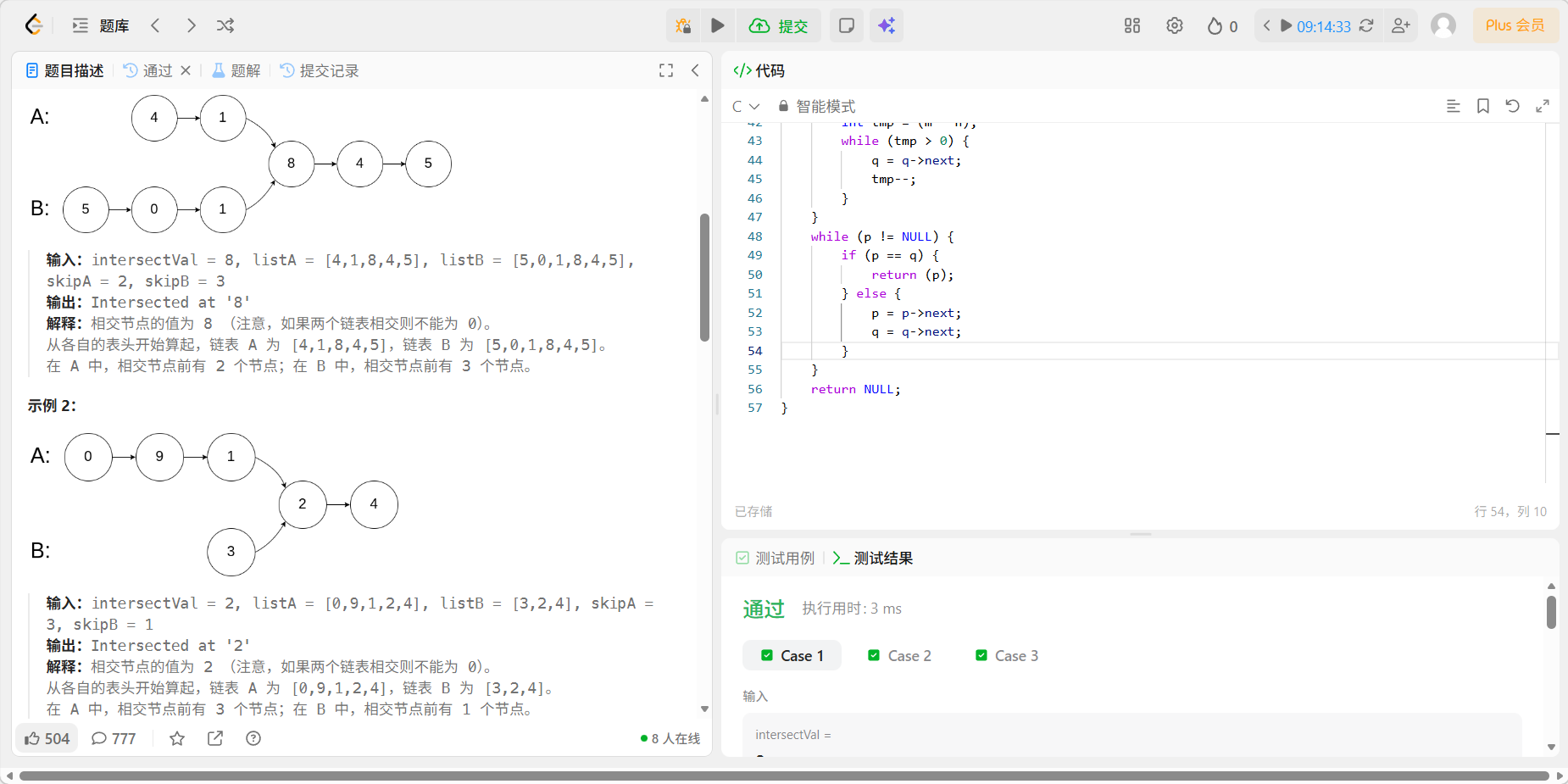
代码

核心思想：快慢指针，先通过while循环得到两个链表的长度n,m，然后让较长的链表先走abs(n-m)步，（也就是尾部对齐）然后同步后移，直到找到交点，否则返回null。

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* getIntersectionNode(struct ListNode* headA,
                                     struct ListNode* headB) {
    struct ListNode dummy1;
    dummy1.next = headA;
    struct ListNode* p = &dummy1;

    struct ListNode dummy2;
    dummy2.next = headB;
    struct ListNode* q = &dummy2;
    if (p->next == NULL || q->next == NULL) {
        return NULL;
    }

    int n = 0;
    while (p->next != NULL) {
        p = p->next;
        n++;
    }

    int m = 0;
    while (q->next != NULL) {
        q = q->next;
        m++;
    }

    p = &dummy1;
    q = &dummy2;
    if ((n - m) > 0) {
        int tmp = (n - m);
        while (tmp > 0) {
            p = p->next;
            tmp--;
        }
    } else if ((n - m) < 0) {
        int tmp = (m - n);
        while (tmp > 0) {
            q = q->next;
            tmp--;
        }
    }
    while (p != NULL) {
        if (p == q) {
            return (p);
        } else {
            p = p->next;
            q = q->next;
        }
    }
    return NULL;
}

时间复杂度：O(n+m) 【n,m分别为链表长度】

空间复杂度：O(1)

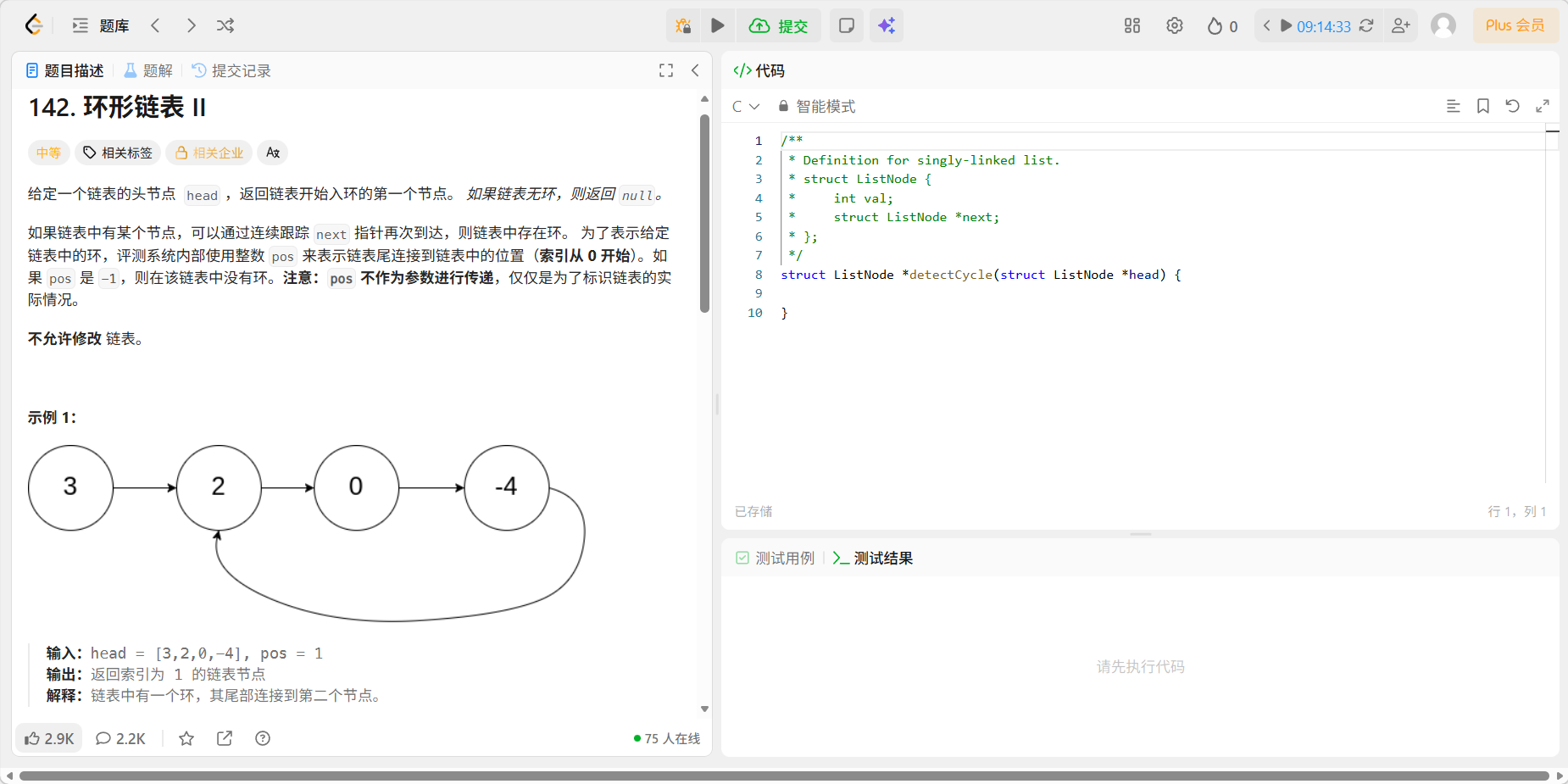
9、142 环形链表 ②

题目

代码

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* detectCycle(struct ListNode* head) {
    if (head == NULL || head->next == NULL) {
        return NULL;
    }
    struct ListNode* p = head;
    struct ListNode* q = head;
    while(p != NULL && p->next != NULL){
        p = p->next->next;
        q = q->next;
        if(p == q){
            struct ListNode* a = head;
            struct ListNode* b = q; 
            while(a != b){
                a = a->next;
                b = b->next;
            }
            return a;
        }
    }
    return NULL;
}

时间复杂度：O(n)

空间复杂度：O(1)
核心思想bygimini

Floyd 判圈算法两步走

第一步：找相遇点

快指针（每次 2 步）和慢指针（每次 1 步）从起点出发。如果相遇，说明有环。

第二步：找入环点

这是一个数学定理：从相遇点和链表起点同时出发，每次各走 1 步，它们再次相遇的地方就是入环点。

关键点详解

while (fast != NULL && fast->next != NULL) ：这是链表题最稳健的写法。它能同时处理链表长度为奇数和偶数的情况，防止 ->next->next 报错。
为什么 head 和 slow 相遇就是入环点？

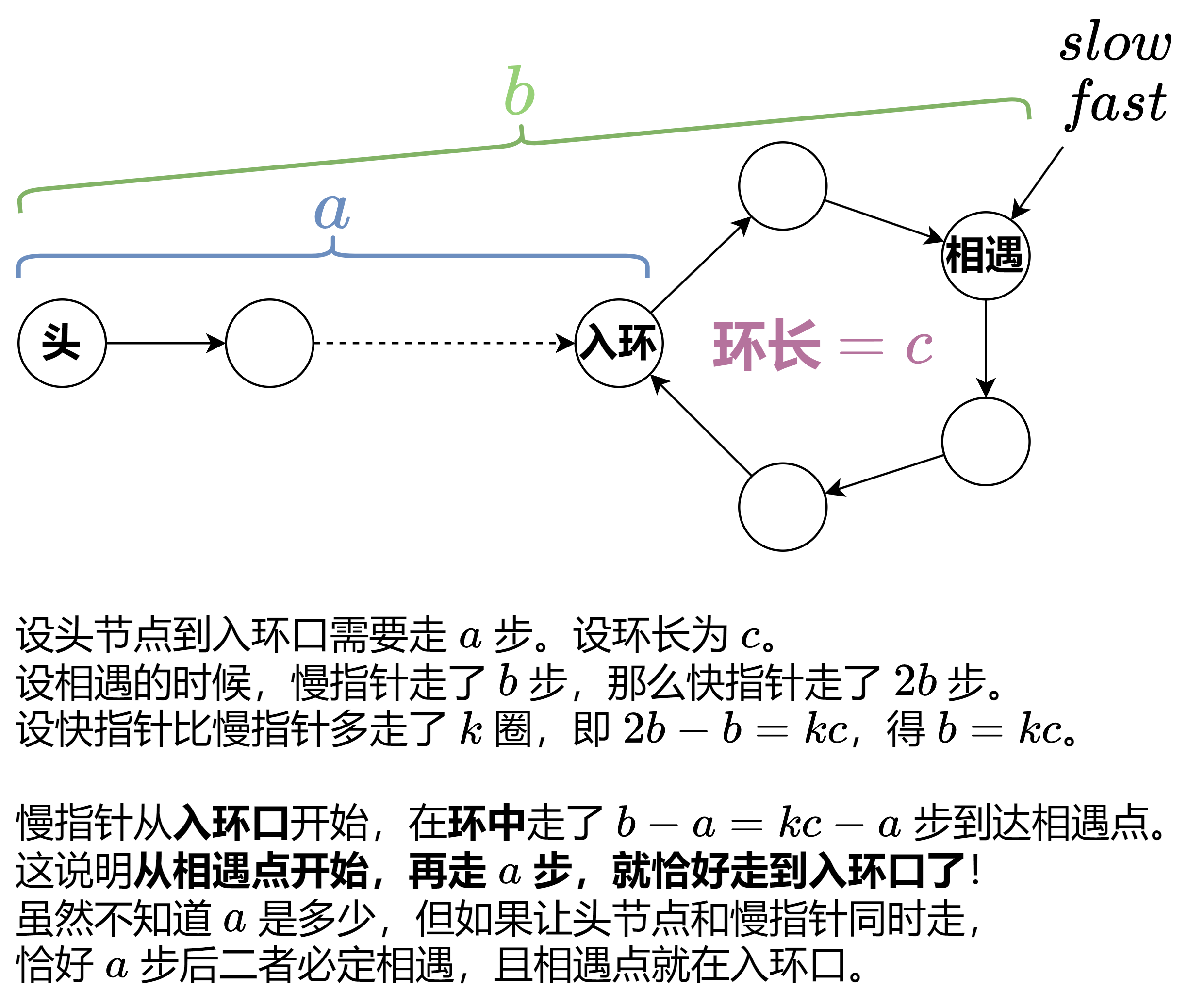
注 1：kc−a 是从入环口开始的步数。因为 (kc−a)+a=kc，所以从 kc−a 开始，再走 a 步，就可以走满 k 圈。

注 2：慢指针从相遇点开始，移动 a 步后恰好走到入环口，但在这个过程中，可能会多次经过入环口。

注 3：这个算法叫做 Floyd 判圈算法。

作者：灵茶山艾府

链接：https://leetcode.cn/problems/linked-list-cycle-ii/solutions/1999271/mei-xiang-ming-bai-yi-ge-shi-pin-jiang-t-nvsq/

来源：力扣（LeetCode）

并推荐看代码随想录的视频更基础更友好环形链表

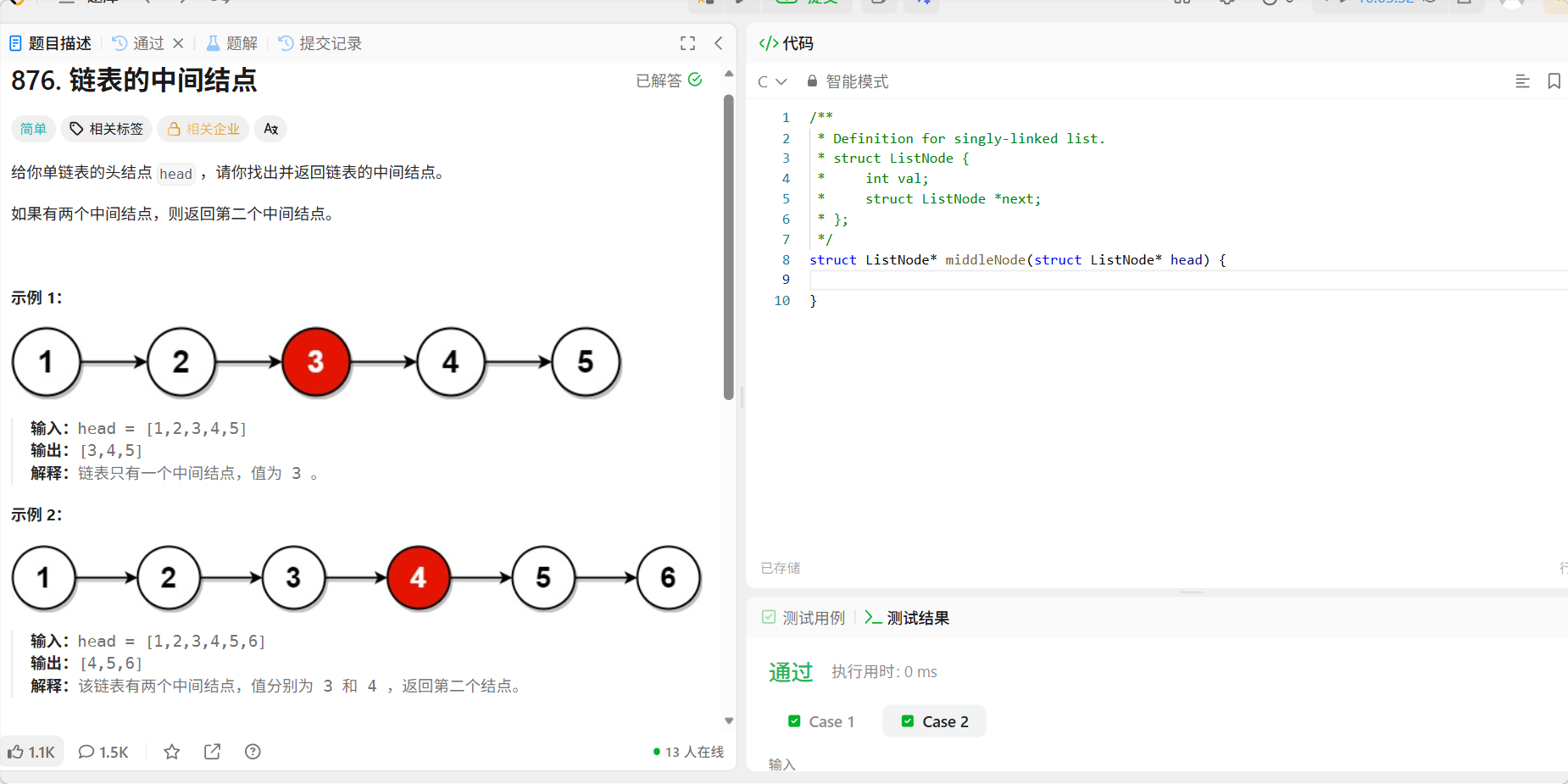
10、876 链表的中间节点

题目：

代码：

暴力解法，先算链表长度，再遍历到1/2的位置。

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* middleNode(struct ListNode* head) {
    struct ListNode* p = head;
    int n = 0;
    while(p != NULL){
        p = p->next;
        n++;
    }
    p = head;
    for(int i = 0;i < (n/2);i++){
        p = p->next;
    }
    return p;
}

时间复杂度：O(n)

空间复杂度：O(1)

另解：

快慢指针，当快指针指向null或者快指针的next指向null时，慢指针指向1/2的位置。

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* middleNode(struct ListNode* head) {
   struct ListNode* p = head;
   struct ListNode* q = head;
   while(p != NULL && p->next != NULL){
        p = p->next->next;
        q = q->next;
   }
   return q;
}

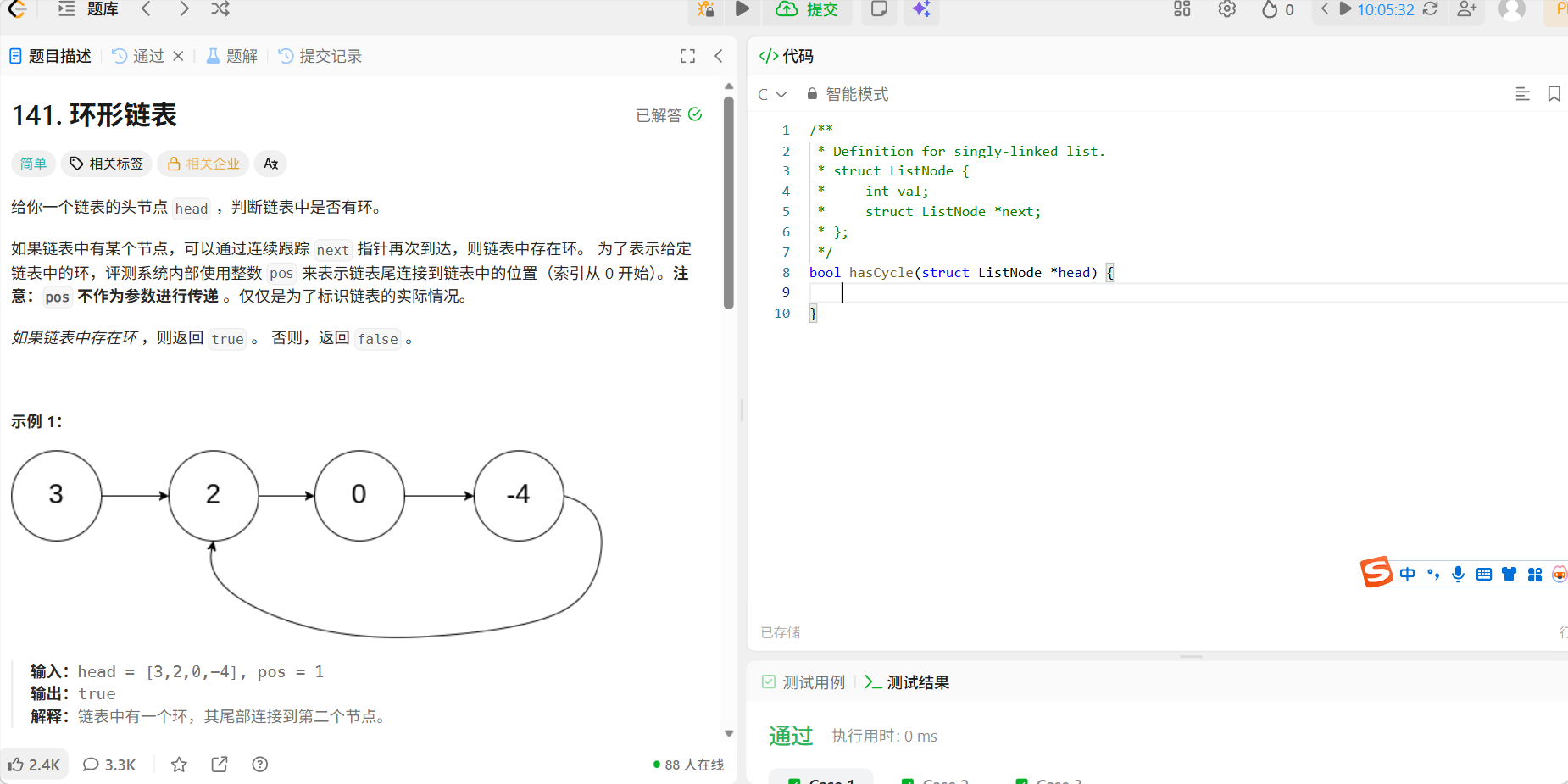
11、141 环形链表

题目

代码

写完142再写141简直易如反掌嘻嘻

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
bool hasCycle(struct ListNode *head) {
    if(head == NULL || head->next == NULL){
        return false;
    }
    struct ListNode* p = head;
    struct ListNode* q = head;

    while(p != NULL && p->next != NULL){
        p = p->next->next;
        q = q->next;
        if(p == q){
            return true;
        }
    }
    return false;
}

时间复杂度：O(n)

空间复杂度：O(1)

12、143 重排链表

题目

代码

结合上述的找链表中间节点和反转链表，先找到链表中间节点，然后反转中间节点及后面的链表节点，然后两个链表各取一个拼接起来就OK啦

c 复制代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
void reorderList(struct ListNode* head) {
    struct ListNode* p = head;
    struct ListNode* q = head;

    while(p != NULL && p->next != NULL){
        p = p->next->next;
        q = q->next;
    }

    struct ListNode dummy;
    dummy.next = q;
    struct ListNode* cur = &dummy;
    cur = dummy.next;
    struct ListNode* pre = NULL;
    while(cur != NULL){
        struct ListNode* nxt = cur->next;
        cur->next = pre;
        pre = cur;
        cur = nxt;
    }
    q = pre;
    p = head;
    while(q->next != NULL){
        struct ListNode* nxt1 = p->next;
        struct ListNode* nxt2 = q->next;
        p->next = q;
        q->next = nxt1;
        p = nxt1;
        q = nxt2;
    }
}

时间复杂度：O(n)

空间复杂度：O(1)

算法刷题--链表

文章目录

1、203 移除链表元素

法二：虚拟头结点法

为什么这段代码更好？

1. 代码逐行直译

2. 为什么要这么做？（核心痛点）

3. 内存与指针的直观图示

4. 这种写法的"高级感"体现在哪？

延伸思考

法三 递归

1. 递归代码实现

2. 递归过程的直观理解

3. 递归法的优缺点

4. 总结与建议

2、707 设计链表

1. 数据结构定义

2. 五大核心操作的解题思路

① 获取节点 get(index)

② 头部插入 addAtHead(val)

③ 尾部插入 addAtTail(val)

④ 按索引插入 addAtIndex(index, val)

⑤ 按索引删除 deleteAtIndex(index)

3. 为什么一定要用虚拟头节点？

4. 常见坑点（避坑指南）

5. 进阶：单链表还是双链表？

3、206 翻转链表

1. 终止条件（Base Case）

2. 递归下钻（Pushing down）

3. 指针逆转逻辑（The Magic Step）

举个例子：假设链表是 1 -> 2 -> 3 -> NULL

4. 为什么要设置 head->next = NULL？

5. 复杂度分析

4、反转链表二

5、25 k个一组翻转链表

6、24 两两交换链表中的节点

1. 核心变量的作用

2. 交换逻辑图解（关键 3 步）

3. 指针迭代更新

4. 循环条件分析

7、 19 删除链表的倒数第N个结点

8、07 链表相交

9、142 环形链表 ②

时间复杂度：O(n)

Floyd 判圈算法两步走

第一步：找相遇点

第二步：找入环点

关键点详解

10、876 链表的中间节点

11、141 环形链表

12、143 重排链表

法三递归

① 获取节点 `get(index)`

② 头部插入 `addAtHead(val)`

③ 尾部插入 `addAtTail(val)`

④ 按索引插入 `addAtIndex(index, val)`

⑤ 按索引删除 `deleteAtIndex(index)`

举个例子：假设链表是 `1 -> 2 -> 3 -> NULL`

4. 为什么要设置 `head->next = NULL`？