算法构建了一个完整的土木工程承载力预测深度学习框架,主要工作流程如下:首先基于Terzaghi经典承载力理论公式生成合成数据集,通过引入随机噪声模拟实际工程的不确定性,同时计算宽长比、埋深比等无量纲工程参数作为特征工程的一部分;接着对数据进行标准化处理并划分为训练集、验证集和测试集,构建包含批量归一化和Dropout层的深度神经网络模型;在训练过程中使用AdamW优化器配合余弦退火学习率调度策略进行参数更新,并设计包含物理约束的损失函数来确保预测结果符合工程常识,如承载力应随土体强度参数单调增加且处于合理范围;完成训练后,算法在测试集上进行全面评估,计算包括均方根误差、R²分数、平均绝对百分比误差在内的多种性能指标,并生成丰富的可视化图表展示训练历史、预测与实测对比、误差分布、特征重要性分析以及参数敏感性研究;最后,算法提供模型解释性分析,通过特征重要性排序和参数化研究揭示各输入参数对承载力的影响规律,还实现了模型保存与加载功能,便于实际工程应用中的部署和推理。整个算法不仅实现了高精度的承载力预测,还通过领域知识嵌入确保了预测结果的物理合理性,为土木工程师提供了一个可靠的数据驱动预测工具。

第一步:合成数据生成与工程特征构造
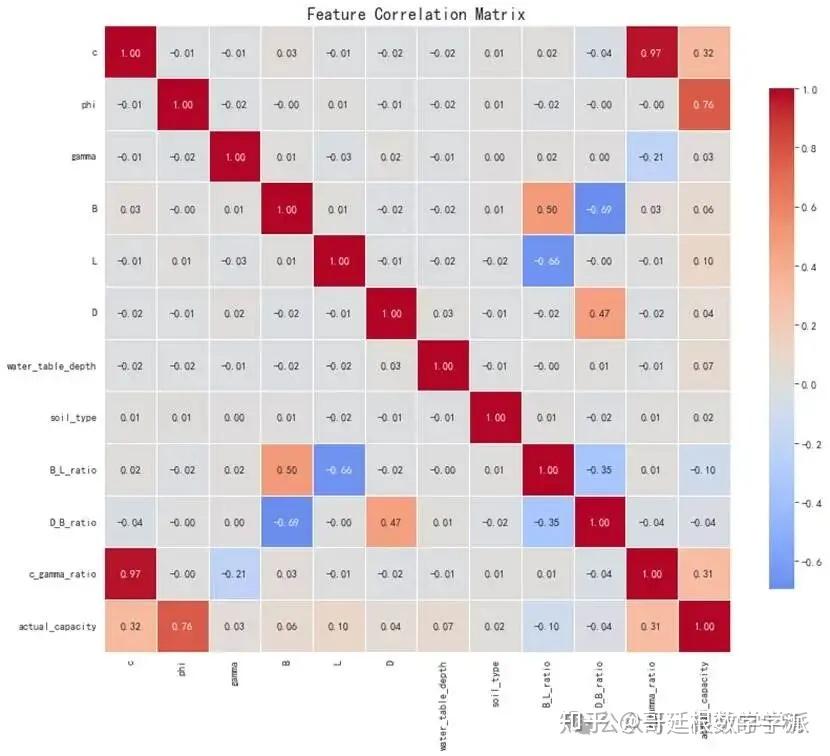
基于Terzaghi经典地基承载力理论公式,随机生成符合工程实际的土体参数,包括粘聚力、内摩擦角、土体重度、基础尺寸、埋深等关键变量。在计算理论承载力值时,考虑地下水影响、基础形状修正等实际工程因素,并添加合理范围的随机噪声模拟现场测试的不确定性。同时,构造宽长比、埋深比等无量纲工程参数作为特征工程的组成部分,增强模型的物理意义。
第二步:数据预处理与标准化转换
对所有输入特征进行标准化处理,使各特征具有零均值和单位方差,消除量纲差异对神经网络训练的影响。将数据集按比例划分为训练集、验证集和测试集三部分,确保模型训练、调参和最终评估的独立性。
第三步:深度神经网络架构设计
构建多层前馈神经网络模型,设计合适的隐藏层数量和神经元个数。在网络中加入批量归一化层加速训练收敛,引入Dropout层防止模型过拟合,使用ReLU激活函数增加非线性表达能力。采用Xavier方法初始化网络权重,为输出层配置线性激活函数以适应回归预测任务。
第四步:物理约束损失函数设计
定义包含领域知识的复合损失函数,在传统均方误差损失基础上,加入单调性约束确保承载力随土体强度参数增加而增加,添加边界约束确保预测值处于工程合理范围,通过权重系数平衡各项损失的贡献度。
第五步:迭代训练与优化过程
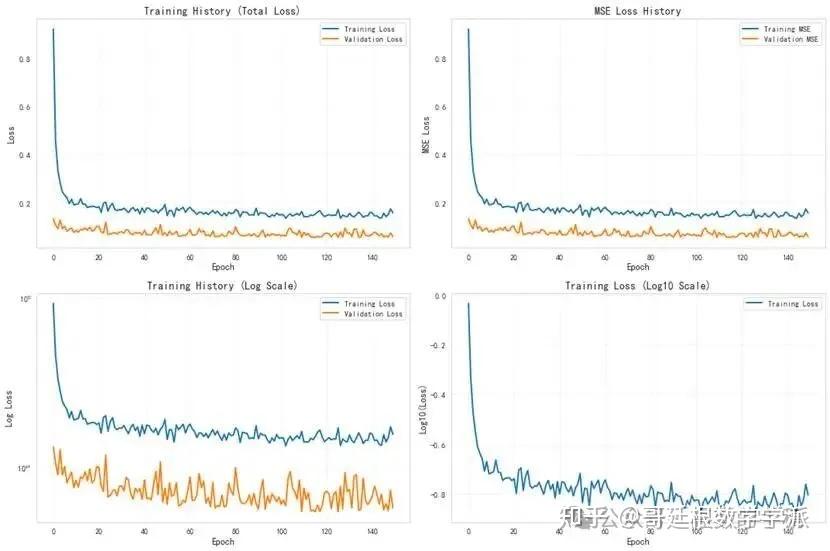
使用AdamW优化器配合权重衰减正则化进行参数更新,设置余弦退火学习率调度策略动态调整学习速率。在每个训练周期内,将数据分成小批量进行前向传播计算预测值,反向传播计算梯度,实施梯度裁剪防止梯度爆炸,更新网络参数。同时在验证集上监控模型性能,实现早停机制防止过拟合。
第六步:模型性能综合评估
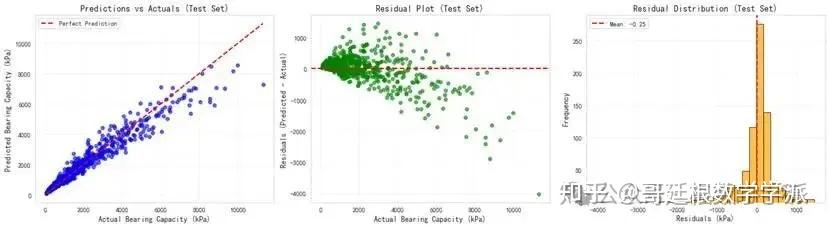
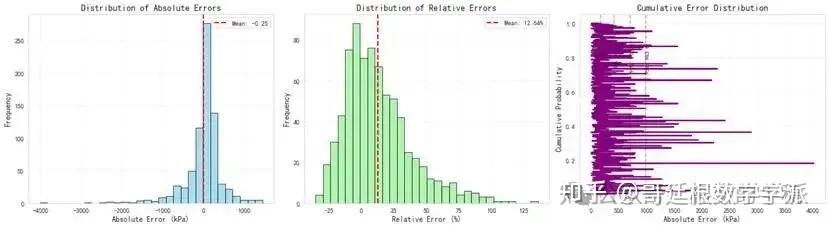
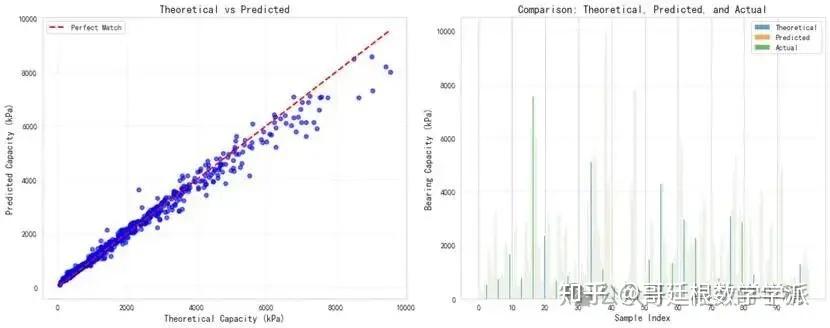
在独立测试集上评估最终模型性能,计算均方根误差、平均绝对误差、平均绝对百分比误差等绝对误差指标,计算决定系数、解释方差、皮尔逊相关系数等相关性指标,统计误差在一定范围内的样本比例。通过对比神经网络预测值与理论公式计算值,验证模型的物理合理性。
第七步:多维可视化分析与解释
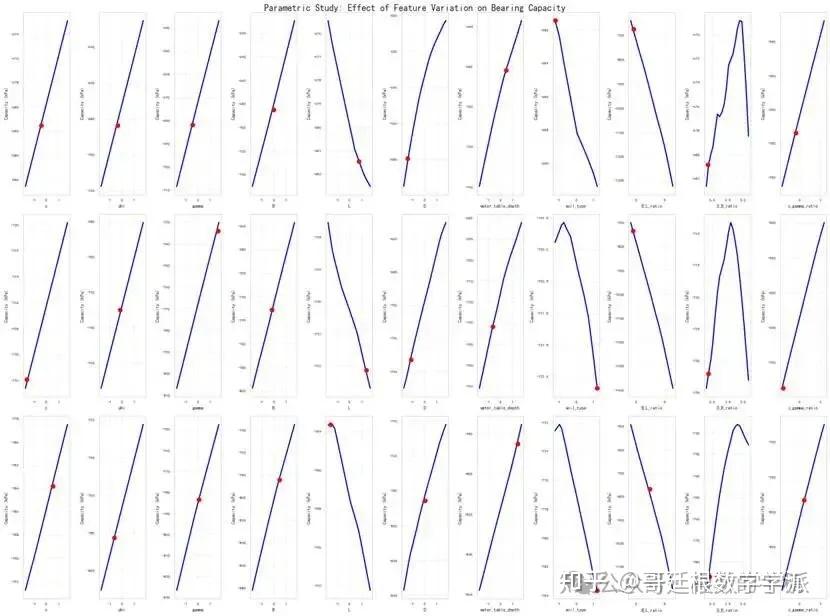
生成训练过程的损失变化曲线图,观察模型收敛情况;绘制预测值与实际值的散点对比图,直观展示预测精度;分析误差分布特征,识别系统偏差;计算特征重要性排序,理解各输入参数对预测结果的贡献程度;进行参数敏感性研究,揭示单变量变化对承载力的影响规律。
"""
承载力预测深度学习模型
嵌入土木工程领域先验知识
"""
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# ==================== 1. 数据生成模块 ====================
class BearingCapacityDataGenerator:
"""基于Terzaghi承载力理论生成合成数据"""
def __init__(self, n_samples=5000, seed=42):
self.n_samples = n_samples
self.seed = seed
np.random.seed(seed)
# 定义参数范围(基于实际工程经验)
self.param_ranges = {
'c': (5, 100), # 粘聚力 (kPa)
'phi': (10, 40), # 内摩擦角 (度)
'gamma': (15, 22), # 土体重度 (kN/m³)
'B': (0.5, 5.0), # 基础宽度 (m)
'L': (1.0, 10.0), # 基础长度 (m)
'D': (0.5, 3.0), # 埋深 (m)
'water_table_depth': (0, 5.0), # 地下水位深度 (m)
'soil_type': [0, 1, 2] # 土体类型: 0-砂土, 1-黏土, 2-粉土
}
def terzaghi_formula(self, c, phi, gamma, B, L, D, Nc, Nq, Ngamma):
"""Terzaghi承载力公式(用于数据生成)"""
# 基本承载力公式
q_ult = c * Nc + gamma * D * Nq + 0.5 * gamma * B * Ngamma
# 添加形状修正(先验知识嵌入)
if B/L < 0.5:
shape_factor = 0.8 + 0.4 * (B/L)
else:
shape_factor = 1.0 - 0.2 * (B/L)
return q_ult * shape_factor
def get_bearing_capacity_factors(self, phi_rad):
"""获取承载力系数(嵌入领域知识)"""
# 使用经典承载力系数公式
Nq = np.exp(np.pi * np.tan(phi_rad)) * (np.tan(np.pi/4 + phi_rad/2))**2
Nc = (Nq - 1) / np.tan(phi_rad) if phi_rad > 0 else 5.14 # φ=0时的理论值
Ngamma = 2 * (Nq + 1) * np.tan(phi_rad) # Meyerhof公式
return Nc, Nq, Ngamma
def generate_data(self):
"""生成合成数据集"""
data = {}
# 生成基本参数
for param, ranges in self.param_ranges.items():
if param == 'soil_type':
data[param] = np.random.choice(ranges, self.n_samples)
else:
data[param] = np.random.uniform(ranges[0], ranges[1], self.n_samples)
df = pd.DataFrame(data)
# 计算无量纲参数(先验知识嵌入)
df['B_L_ratio'] = df['B'] / df['L'] # 宽长比
df['D_B_ratio'] = df['D'] / df['B'] # 埋深比
df['phi_rad'] = np.radians(df['phi']) # 角度转弧度
# 生成理论承载力(作为基准)
theoretical_capacity = []
for idx, row in df.iterrows():
phi_rad = row['phi_rad']
Nc, Nq, Ngamma = self.get_bearing_capacity_factors(phi_rad)
# 地下水影响修正(先验知识)
gamma_eff = row['gamma']
if row['water_table_depth'] < row['D']:
gamma_eff = row['gamma'] - 9.8 # 考虑浮重度
# 计算承载力 - 修正了参数传递
q_ult = self.terzaghi_formula(
row['c'], row['phi'], gamma_eff,
row['B'], row['L'], row['D'], Nc, Nq, Ngamma
)
theoretical_capacity.append(q_ult)
df['theoretical_capacity'] = theoretical_capacity
# 添加随机噪声(模拟实际工程不确定性)
noise = np.random.normal(0, 0.15, self.n_samples) # 15%的噪声
df['actual_capacity'] = df['theoretical_capacity'] * (1 + noise)
# 确保承载力为正数
df['actual_capacity'] = np.maximum(df['actual_capacity'], 50)
# 添加一些工程衍生特征
df['c_gamma_ratio'] = df['c'] / df['gamma'] # 粘聚力与重度的比值
df['capacity_per_area'] = df['actual_capacity'] / (df['B'] * df['L']) # 单位面积承载力
return df参考文章:
基于物理信息嵌入与多维度约束的深度学习地基承载力智能预测与可解释性评估算法(以模拟信号为例,Pytorch) - 哥廷根数学学派的文章
https://zhuanlan.zhihu.com/p/1993602936241144062