算法十日谈：双指针

一、用途

使用双指针的目的无非两种，其一是控制距离，其二是区间维护。

控制距离时使用的双指针称为快慢指针，又称龟兔赛跑算法，在处理循环链表或者数组时较为常用，其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列结构上移动，但实际上只要遇到循环结构都可以考虑使用快慢指针来判定循环。

区间维护时使用的双指针称为对撞指针，又称左右指针，在处理顺序结构时较为常用，其基本思想就是使用两个指针从两端向中间移动，其难点一般在于边界情况的处理。

二、例题

2.1 移动零

链接：移动零

只考虑两个因素：一是下一个非零元素存放的位置，二是下一个非零元素，每次都将非零元素移动至目标位置，这样就可以在一次遍历中直接完成，代码实现如下

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int slow = 0; //记录下一个存放非0元素的位置
        int n = nums.size();
        for(int fast = 0; fast < n; fast ++){ //fast记录下一个非0元素
            if (nums[fast] != 0) {
                if (slow != fast) {
                    swap(nums[slow], nums[fast]);
                }
                slow++;
            }
        }
    }
};

2.2 复写零

链接：复写零

这题从头开始处理的话会出现一个问题，就是被复写0覆盖元素的存储，所以从后往前看，先确定复写数组在的最后一个元素在原始数组中的位置，然后从后向前覆盖，代码实现如下

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int n = arr.size(); //数组规模
        int num = 0; //复写数组与原数组之间的偏移量
        int tmp = 0; //用于处理复写时溢出的边界情况
        for(int i = 0; i < n - 1; i++){
            if(arr[i] == 0){
                num++;
                tmp++;
            }
            tmp++;
            if(tmp > n-1){
                break;
            }
        }
        int fast = n-1-num;
        int slow = n-1;
        if(tmp == n + 1){ //数组溢出，处理边界情况
            arr[n-1] = 0; 
            slow--;
        }
        while(fast >= 0){
            if(arr[fast] == 0){
                arr[slow] = 0;
                arr[slow-1] = 0;
                slow = slow - 2;
            }else{
                arr[slow] = arr[fast];
                slow--;
            }
            fast--;
        }
    }
};

2.3 快乐数

链接：快乐数

这题的结果有两种可能，一种是经过若干次迭代后回到1，一种是循环，既然出现了循环，那就可以考虑双指针，其中慢指针每次运算一次，快指针每次运算两次，如果快慢指针最终相遇且不为1，则输出false，否则为true，代码实现如下

class Solution {
public:
    bool isHappy(int n) {
        int slow = n;
        int fast = func(slow);
        while (slow != fast){
            slow = func(slow);           //慢指针每次运算一次
            fast = func(func(fast));     //快指针每次运算两次
        }
        if(slow == 1 || fast == 1){
            return true;                 //任意指针先抵达1则为快乐数
        }
        return false;
    }

    int func(int n){
        int ret = 0;
        while(n > 0){
            int tmp = n % 10;
            ret += tmp * tmp;
            n = n / 10;
        }
        return ret;
    }
};

2.4 盛最多水的容器

链接：盛最多水的容器

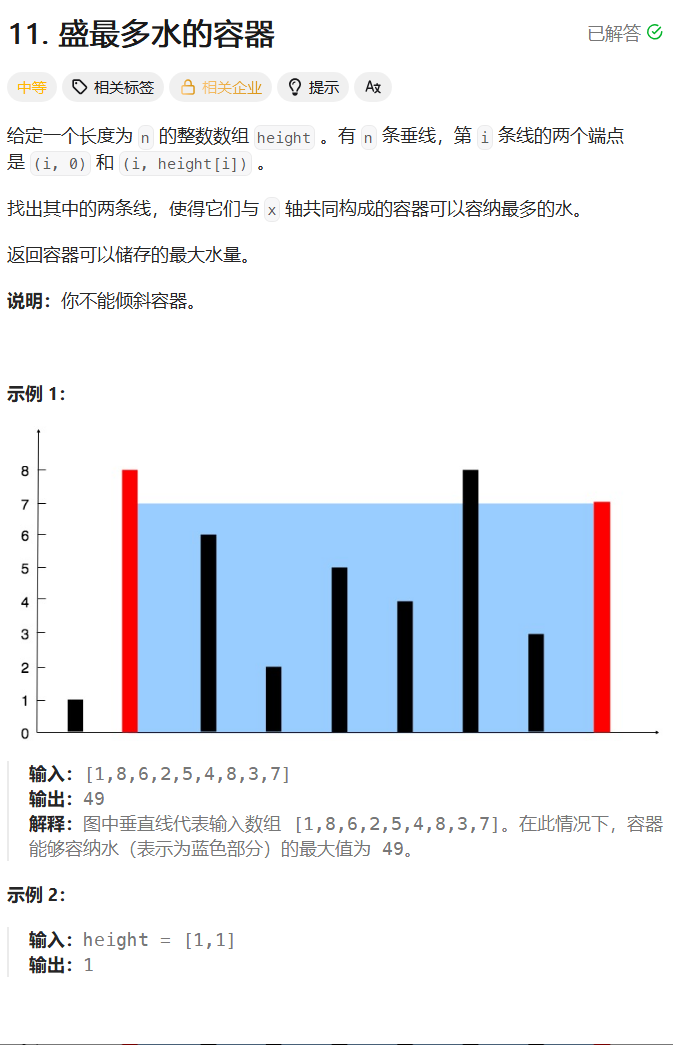
这题需要确定的因素有两个，一个是两个边界中的较小值，也就是高，另一个则是两个边界之间的距离，也就是底，考虑从两端向中间使用对撞指针，每次使较短的边界向内移动，过程中不断迭代最大值，最后输出过程中的最大值。

这里对于移动较短边界进行证明，假设当前两个边界分别为a和b（a<b），底为s，此时面积为a*s，若将b向内移动，假设移动后为b1，则当b1≥a时，更新后的面积为a*(s-1)<a*s；当b1<a时，更新后的面积为b1*(s-1)<a*s，无论哪一种都会导致面积变小，因此移动较短边界。

代码实现如下

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left = 0;           //左边界
        int right = n-1;        //右边界
        int ret = 0;            //当前最大面积
        while(left < right){
            if(height[left] < height[right]){
                int tmp = (right - left) * height[left];
                ret = ret > tmp ? ret : tmp;   //取当前面积与当前最大面积的较大值
                left++;
            }else{
                int tmp = (right - left) * height[right];
                ret = ret > tmp ? ret : tmp;
                right--;
            }
        }
        return ret;
    }
};

2.5 有效三角形的个数

链接：有效三角形的个数

对于乱序数组而言，这题就只能使用三层for循环来暴力求解，时间复杂度O(n^3)百分百过不了，因此考虑先将数组变成顺序数组后，每次循环固定最大边c，统计最小边a和次大边b的组合（对任意三角形，总有较小的两边之和大于第三边），代码实现如下

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        int max = n - 1;
        int ret = 0;
        int begin = 0;
        while(begin < n && nums[begin] == 0){
            begin++;
        }
        while(max > 1){
            int left = begin;       //初始化左边界
            int right = max - 1;    //初始化右边界
            while(left < right){
                if(nums[left] + nums[right] > nums[max]){
                    ret += right - left;
                    --right;        //已确定最小和最大边，统计次大边
                }
                else{
                    ++left;         //已确定最大和次大边，统计最小边
                }
            }
            max--;
        }
        return ret;
    }
};

2.6 查找总价值为目标值的两个商品

链接：查找总价值为目标值的两个商品

这题使用对撞指针，只需完成三种处理即可。

其一，price[left] + price[right] == target，直接返回。

其二，price[left] + price[right] > target，此时对于left而言，如果继续右移就会使二者之和更大，离结果更远，因此需使right左移。

其三，price[left] + price[right] < target，同理，此时需使left右移。

代码实现如下

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int left = 0, right = price.size() - 1;
        while(left < right){
            int sum = price[left] + price[right];
            if(sum > target) right--;
            else if(sum < target) left++;
            else return {price[left], price[right]};
        }
        return {1, -1}; //此处随意填写，仅为满足函数格式，实际不调用
    }
};

2.7 三数之和

链接：三数之和

这题求解三数之和，可以考虑将一个数nums[i]固定，将另外两个数以和为-nums[i]形式求解，即可降级为上题的两数之和，代码实现如下

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();                //数组大小
        sort(nums.begin(), nums.end());     //数组排序，方便处理
        vector<vector<int>> ans;
        for(int i = 0; i < n; i++){
            if(i > 0 && nums[i] == nums[i-1]){
                continue;
            }
            int k = n-1;
            int target = - nums[i];         //另外两数的目标和
            for(int j = i + 1; j < n; j++){
                if(j > i + 1 && nums[j] == nums[j-1]){
                    continue;
                }
                while(j < k && nums[j] + nums[k] > target){
                    k--;
                }
                if(j == k){
                    break;
                }
                if(nums[j] + nums[k] == target){
                    ans.push_back({nums[i], nums[j], nums[k]});
                }
            }
        }
        return ans;
    }
};

2.8 四数之和

链接：四数之和

这题求解四数之和，类似上题，考虑固定一个数后再固定一个数，实现问题的降解，同理可以推广至n数之和，都可以用类似的方式，代码实现如下

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        vector<vector<int>> ans;
        for(int a = 0; a < n; a++){                 //固定第一个数
            if(a > 0 && nums[a] == nums[a-1]){
                continue;
            }
            for(int b = a + 1; b < n; b++){         //固定第二个数
                if(b > a + 1 && nums[b] == nums[b-1]){
                    continue;
                }
                if(nums[b] >= 0 && nums[a] + nums[b] > target){
                    break;
                }
                long tmp = - (long)nums[a] - (long)nums[b] + (long)target; //此处使用long是因为原题用例中会出现int溢出的情况，使用long可以避免报错
                int d = n - 1;
                for(int c = b + 1; c < n; c++){
                    if(c > b + 1 && nums[c] == nums[c-1]){
                        continue;
                    }
                    while(c < d && (long)nums[c] + (long)nums[d] > tmp){
                        d--;
                    }
                    if(c == d){
                        break;
                    }
                    if(nums[c] + nums[d] == tmp){
                        ans.push_back({nums[a], nums[b], nums[c], nums[d]});
                    }
                }
            }
        }
        return ans;
    }
};