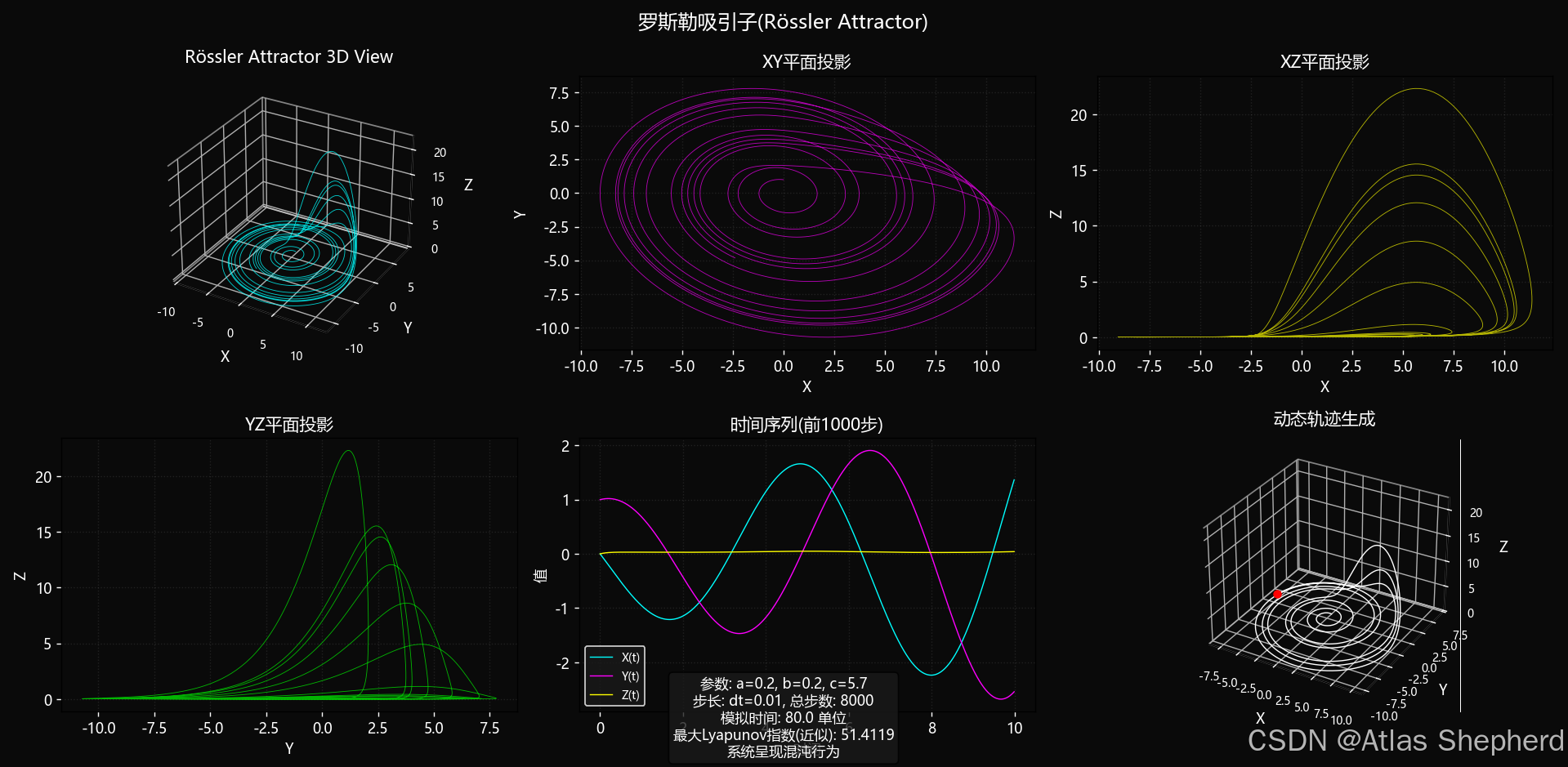
python实现罗斯勒吸引子(Rössler Attractor)

2301_764441332026-01-14 11:42

罗斯勒吸引子(Rössler Attractor)

1. 理论基础与数学模型

1.1 罗斯勒系统简介

罗斯勒吸引子是德国科学家奥托·罗斯勒(Otto Rössler)于1976年提出的一种混沌系统，是继洛伦兹吸引子之后第二个被发现的混沌吸引子。相比洛伦兹吸引子的双涡卷结构，罗斯勒吸引子具有更简洁的数学形式，但同样能产生丰富的混沌动力学行为。

1.2 微分方程描述

罗斯勒系统的控制方程为：

复制代码 
dx/dt = -y - z
dy/dt = x + a*y
dz/dt = b + z*(x - c)

其中：

  • a, b, c​ 是系统参数

  • **(x, y, z)**​ 是系统的状态变量

  • 经典参数值：a=0.2, b=0.2, c=5.7

1.3 物理意义解读

  • x方程：-y - z 表示x的变化受y和z的负反馈

  • y方程：x + a*y 表示y的变化是x的线性驱动和自身衰减

  • z方程 ：b + z*(x - c) 包含常数项b和非线性耦合项z*(x-c)，这是系统产生混沌的关键

2. 代码架构分析

2.1 类设计(RosslerAttractor)

代码采用面向对象设计，将罗斯勒系统封装为一个类，主要包含：

2.1.1 核心属性

  • 系统参数：a, b, c

  • 时间参数：dt(步长), steps(步数)

  • 状态变量：x, y, z轨迹数组

  • 时间向量：t

2.1.2 核心方法

  1. **simulate()**​ - 数值模拟

  2. **calculate_lyapunov()**​ - 李雅普诺夫指数计算

  3. **create_animation()**​ - 可视化动画

  4. **explore_parameters()**​ - 参数探索

2.2 数值方法实现

2.2.1 欧拉法(Euler Method)
复制代码 
# 一阶精度，计算简单但精度有限
dx = (-y - z) * dt
dy = (x + a*y) * dt
dz = (b + z*(x - c)) * dt
2.2.2 四阶龙格-库塔法(RK4)
复制代码 
# 四阶精度，稳定性好，适用于混沌系统
# 通过四个中间斜率(k1,k2,k3,k4)加权平均
# 显著提高计算精度

比较：

  • 欧拉法：计算简单，但dt过大会导致发散

  • RK4法：精度高，适合混沌系统模拟，但计算量较大

  • 本代码默认使用RK4法以保证模拟精度

3. 混沌特征分析

3.1 李雅普诺夫指数(Lyapunov Exponent)

代码中实现了李雅普诺夫指数的近似计算：

复制代码 
def calculate_lyapunov(self, epsilon=1e-8, steps=1000):
    # 主轨迹和扰动轨迹分离计算
    # 计算相邻轨线的指数发散率
    # λ = (1/t) * Σ ln(d(t)/d₀)

物理意义：

  • λ > 0：系统对初始条件敏感（混沌）

  • λ = 0：系统处于临界状态

  • λ < 0：系统稳定收敛

3.2 相空间重构

代码展示的多种投影方式：

  1. 3D完整相空间：展示吸引子全貌

  2. XY平面投影：显示螺旋结构

  3. XZ平面投影：显示折叠特性

  4. YZ平面投影：显示非线性特征

4. 可视化技术详解

4.1 多图布局设计

复制代码 
┌─────────────┬─────────────┬─────────────┐
│    3D视图    │   XY投影    │   XZ投影    │
├─────────────┼─────────────┼─────────────┤
│    YZ投影    │  时间序列    │  动态生成    │
└─────────────┴─────────────┴─────────────┘

4.2 动画实现原理

复制代码 
# 使用FuncAnimation创建帧动画
anim = FuncAnimation(fig, update, frames=..., interval=20, blit=True)

# 更新函数控制轨迹绘制
def update(frame):
    idx = min(frame * 20, len(self.x) - 1)
    line.set_data(self.x[:idx], self.y[:idx])
    line.set_3d_properties(self.z[:idx])

4.3 颜色与视觉效果

  • 深色背景：突出轨迹，减少视觉干扰

  • 霓虹色彩：增强科技感和可区分性

  • 透明度控制：展现轨迹密度

  • 网格线：提供空间参考

5. 参数空间探索

5.1 经典参数组合

代码预设了6种参数组合：

参数(a,b,c) 系统行为 特征
(0.2,0.2,2.0) 周期轨道 稳定极限环
(0.2,0.2,3.5) 准周期轨道 双周期运动
(0.2,0.2,5.7) 经典混沌 标准吸引子
(0.2,0.2,9.0) 高维混沌 复杂轨迹
(0.1,0.1,14.0) 双涡卷结构 类似洛伦兹
(0.2,0.1,5.7) 非对称吸引子 偏斜结构

5.2 参数影响规律

  1. 参数a：影响y方向的阻尼特性

  2. 参数b：影响z方向的常数驱动

  3. 参数c：控制非线性强度，决定混沌行为

6. 数值稳定性与精度

6.1 步长选择原则

复制代码 
dt = 0.01  # 经验值，平衡精度与计算量
steps = 8000  # 足够长的轨迹以展示吸引子

步长选择考虑：

  • dt过小：计算量大，累计误差

  • dt过大：数值不稳定，可能发散

  • 推荐范围：0.001-0.05

6.2 初始条件敏感性

复制代码 
x0, y0, z0 = 0.0, 1.0, 0.0  # 经典初始条件

混沌系统的特点是对初始条件极度敏感，但吸引子结构是稳定的。

7. 系统特性分析

7.1 固定点分析

令dx/dt = dy/dt = dz/dt = 0：

复制代码 
-y - z = 0
x + a*y = 0
b + z*(x - c) = 0

解得两个固定点，其稳定性由雅可比矩阵特征值决定。

7.2 Poincaré截面

可通过记录轨迹与特定平面的交点来研究系统的截面特征。

7.3 功率谱分析

（代码中未实现）可通过傅里叶变换分析频率特征，混沌系统具有连续宽带谱。

8. 实际应用场景

8.1 教学演示

  • 混沌理论教学

  • 非线性动力学入门

  • 数值方法实践

8.2 科学研究

  • 混沌控制与同步研究

  • 混沌加密算法测试

  • 复杂系统建模参考

8.3 艺术生成

  • 生成艺术图案

  • 动态视觉效果

  • 音乐合成算法

9. 代码优化建议

9.1 性能优化

复制代码 
# 可考虑使用Numba加速数值计算
@jit(nopython=True)
def simulate_jit(...):
    # 使用即时编译加速循环

9.2 功能扩展

  1. 分岔图绘制：研究参数变化时的系统行为

  2. 庞加莱映射：分析截面特性

  3. 相关维数计算：定量描述吸引子复杂度

  4. 实时参数调节：交互式探索

9.3 错误处理增强

复制代码 
# 添加参数合法性检查
if a <= 0 or b <= 0 or c <= 0:
    raise ValueError("参数必须为正数")

10. 运行与使用说明

10.1 环境要求

复制代码 
Python 3.6+
NumPy
Matplotlib
可选：Jupyter环境

10.2 运行方式

复制代码 
# 直接运行
python rossler_attractor.py

# 在Jupyter中
%run rossler_attractor.py

10.3 输出结果

  1. 控制台输出：参数、李雅普诺夫指数、统计信息

  2. 图形窗口1：完整可视化（3D+2D+时间序列+动画）

  3. 图形窗口2：参数空间探索

11. 数学与物理意义总结

11.1 混沌特征验证

  1. 对初始条件敏感：微小的初始差异指数放大

  2. 有限相空间：轨迹不无限发散

  3. 有界非周期：既不收敛到固定点，也不形成周期轨道

  4. 分数维：吸引子具有分数维的几何结构

11.2 与洛伦兹吸引子对比

特性 罗斯勒吸引子 洛伦兹吸引子
方程数 3 3
非线性项 1个(z*(x-c)) 2个(xy, xz)
对称性 不对称 关于z轴对称
复杂度 相对简单 更复杂
应用领域 化学、生物 气象、流体

12. 完整代码

罗斯勒吸引子虽然数学形式简单，但却能产生丰富的复杂行为，是理解混沌理论、非线性动力学的理想模型。这个实现为相关领域的学习和研究提供了一个实用工具。

复制代码 
"""
罗斯勒吸引子(Rössler Attractor)完整实现
无需用户交互，完全自动化运行
"""
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation
import matplotlib.font_manager as fm
import sys
import warnings
import platform

# 忽略警告
warnings.filterwarnings('ignore')

# 配置使用系统字体
if platform.system() == 'Windows':
    # Windows系统使用微软雅黑或黑体
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'Arial Unicode MS']
elif platform.system() == 'Darwin':
    # macOS系统使用PingFang SC或Heiti TC
    plt.rcParams['font.sans-serif'] = ['PingFang SC', 'Heiti TC', 'STHeiti']
else:
    # Linux系统使用文泉驿微米黑或黑体
    plt.rcParams['font.sans-serif'] = ['WenQuanYi Micro Hei', 'SimHei', 'DejaVu Sans']

# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False



class RosslerAttractor:
    """
    罗斯勒吸引子(Rössler Attractor)模拟类
    微分方程：
        dx/dt = -y - z
        dy/dt = x + a*y
        dz/dt = b + z*(x - c)
    """

    def __init__(self, a=0.2, b=0.2, c=5.7, dt=0.01, steps=8000):
        """
        初始化罗斯勒吸引子参数

        参数:
            a, b, c: 系统参数（经典值: 0.2, 0.2, 5.7）
            dt: 时间步长
            steps: 模拟步数
        """
        self.a = a
        self.b = b
        self.c = c
        self.dt = dt
        self.steps = steps

        # 初始条件
        self.x0, self.y0, self.z0 = 0.0, 1.0, 0.0

        # 轨迹数组
        self.x = np.zeros(steps)
        self.y = np.zeros(steps)
        self.z = np.zeros(steps)
        self.t = np.arange(0, steps * dt, dt)

    def simulate(self, method='rk4'):
        """
        使用数值方法求解微分方程

        参数:
            method: 数值方法 ('euler' 或 'rk4')
        """
        # 设置初始条件
        self.x[0], self.y[0], self.z[0] = self.x0, self.y0, self.z0

        if method == 'euler':
            # 欧拉法
            for i in range(1, self.steps):
                dx = (-self.y[i - 1] - self.z[i - 1]) * self.dt
                dy = (self.x[i - 1] + self.a * self.y[i - 1]) * self.dt
                dz = (self.b + self.z[i - 1] * (self.x[i - 1] - self.c)) * self.dt

                self.x[i] = self.x[i - 1] + dx
                self.y[i] = self.y[i - 1] + dy
                self.z[i] = self.z[i - 1] + dz

        elif method == 'rk4':
            # 四阶龙格-库塔法（更高精度）
            for i in range(1, self.steps):
                # k1
                k1x = -self.y[i - 1] - self.z[i - 1]
                k1y = self.x[i - 1] + self.a * self.y[i - 1]
                k1z = self.b + self.z[i - 1] * (self.x[i - 1] - self.c)

                # k2
                x_temp = self.x[i - 1] + 0.5 * self.dt * k1x
                y_temp = self.y[i - 1] + 0.5 * self.dt * k1y
                z_temp = self.z[i - 1] + 0.5 * self.dt * k1z

                k2x = -y_temp - z_temp
                k2y = x_temp + self.a * y_temp
                k2z = self.b + z_temp * (x_temp - self.c)

                # k3
                x_temp = self.x[i - 1] + 0.5 * self.dt * k2x
                y_temp = self.y[i - 1] + 0.5 * self.dt * k2y
                z_temp = self.z[i - 1] + 0.5 * self.dt * k2z

                k3x = -y_temp - z_temp
                k3y = x_temp + self.a * y_temp
                k3z = self.b + z_temp * (x_temp - self.c)

                # k4
                x_temp = self.x[i - 1] + self.dt * k3x
                y_temp = self.y[i - 1] + self.dt * k3y
                z_temp = self.z[i - 1] + self.dt * k3z

                k4x = -y_temp - z_temp
                k4y = x_temp + self.a * y_temp
                k4z = self.b + z_temp * (x_temp - self.c)

                # 更新位置
                self.x[i] = self.x[i - 1] + (self.dt / 6.0) * (k1x + 2 * k2x + 2 * k3x + k4x)
                self.y[i] = self.y[i - 1] + (self.dt / 6.0) * (k1y + 2 * k2y + 2 * k3y + k4y)
                self.z[i] = self.z[i - 1] + (self.dt / 6.0) * (k1z + 2 * k2z + 2 * k3z + k4z)

    def calculate_lyapunov(self, epsilon=1e-8, steps=1000):
        """
        计算最大Lyapunov指数（近似值）

        参数:
            epsilon: 扰动大小
            steps: 计算步数

        返回:
            最大Lyapunov指数近似值
        """
        # 主轨迹
        x_main, y_main, z_main = self.x0, self.y0, self.z0

        # 扰动轨迹
        x_pert = x_main + epsilon
        y_pert = y_main
        z_pert = z_main

        divergence_sum = 0

        for _ in range(steps):
            # 更新主轨迹（简化欧拉法）
            dx_main = (-y_main - z_main) * self.dt
            dy_main = (x_main + self.a * y_main) * self.dt
            dz_main = (self.b + z_main * (x_main - self.c)) * self.dt

            x_main += dx_main
            y_main += dy_main
            z_main += dz_main

            # 更新扰动轨迹
            dx_pert = (-y_pert - z_pert) * self.dt
            dy_pert = (x_pert + self.a * y_pert) * self.dt
            dz_pert = (self.b + z_pert * (x_pert - self.c)) * self.dt

            x_pert += dx_pert
            y_pert += dy_pert
            z_pert += dz_pert

            # 计算距离
            dist = np.sqrt((x_pert - x_main) ** 2 + (y_pert - y_main) ** 2 + (z_pert - z_main) ** 2)

            if dist > 0:
                divergence_sum += np.log(dist / epsilon)

        return divergence_sum / (steps * self.dt)

    def create_animation(self, save_gif=False, filename="rossler_attractor.gif"):
        """创建并运行动画"""
        # 运行模拟
        self.simulate(method='rk4')

        # 创建图形
        fig = plt.figure(figsize=(15, 10))
        fig.patch.set_facecolor('#0a0a0a')

        # 3D轨迹图
        ax1 = fig.add_subplot(231, projection='3d')
        ax1.set_facecolor('#0a0a0a')
        ax1.plot(self.x, self.y, self.z, lw=0.5, alpha=0.8, color='#00ffff')
        ax1.set_xlabel('X', color='white', fontsize=10)
        ax1.set_ylabel('Y', color='white', fontsize=10)
        ax1.set_zlabel('Z', color='white', fontsize=10)
        ax1.tick_params(colors='white', labelsize=8)
        ax1.set_title('Rössler Attractor 3D View', color='white', fontsize=12, pad=10)
        ax1.xaxis.pane.fill = False
        ax1.yaxis.pane.fill = False
        ax1.zaxis.pane.fill = False
        ax1.xaxis.pane.set_edgecolor('white')
        ax1.yaxis.pane.set_edgecolor('white')
        ax1.zaxis.pane.set_edgecolor('white')
        ax1.grid(True, alpha=0.2, linestyle=':', color='gray')

        # 2D投影图
        ax2 = fig.add_subplot(232)
        ax2.set_facecolor('#0a0a0a')
        ax2.plot(self.x, self.y, lw=0.5, alpha=0.7, color='#ff00ff')
        ax2.set_xlabel('X', color='white', fontsize=10)
        ax2.set_ylabel('Y', color='white', fontsize=10)
        ax2.tick_params(colors='white')
        ax2.set_title('XY平面投影', color='white', fontsize=12)
        ax2.grid(True, alpha=0.2, linestyle=':', color='gray')

        ax3 = fig.add_subplot(233)
        ax3.set_facecolor('#0a0a0a')
        ax3.plot(self.x, self.z, lw=0.5, alpha=0.7, color='#ffff00')
        ax3.set_xlabel('X', color='white', fontsize=10)
        ax3.set_ylabel('Z', color='white', fontsize=10)
        ax3.tick_params(colors='white')
        ax3.set_title('XZ平面投影', color='white', fontsize=12)
        ax3.grid(True, alpha=0.2, linestyle=':', color='gray')

        ax4 = fig.add_subplot(234)
        ax4.set_facecolor('#0a0a0a')
        ax4.plot(self.y, self.z, lw=0.5, alpha=0.7, color='#00ff00')
        ax4.set_xlabel('Y', color='white', fontsize=10)
        ax4.set_ylabel('Z', color='white', fontsize=10)
        ax4.tick_params(colors='white')
        ax4.set_title('YZ平面投影', color='white', fontsize=12)
        ax4.grid(True, alpha=0.2, linestyle=':', color='gray')

        # 时间序列图
        ax5 = fig.add_subplot(235)
        ax5.set_facecolor('#0a0a0a')
        ax5.plot(self.t[:1000], self.x[:1000], lw=0.8, label='X(t)', color='#00ffff')
        ax5.plot(self.t[:1000], self.y[:1000], lw=0.8, label='Y(t)', color='#ff00ff')
        ax5.plot(self.t[:1000], self.z[:1000], lw=0.8, label='Z(t)', color='#ffff00')
        ax5.set_xlabel('时间', color='white', fontsize=10)
        ax5.set_ylabel('值', color='white', fontsize=10)
        ax5.tick_params(colors='white')
        ax5.set_title('时间序列(前1000步)', color='white', fontsize=12)
        ax5.legend(facecolor='#1a1a1a', edgecolor='white', labelcolor='white', fontsize=8)
        ax5.grid(True, alpha=0.2, linestyle=':', color='gray')

        # 相位空间图（动态）
        ax6 = fig.add_subplot(236, projection='3d')
        ax6.set_facecolor('#0a0a0a')
        line, = ax6.plot([], [], [], lw=0.8, color='white')
        point, = ax6.plot([], [], [], 'o', markersize=5, color='red')

        ax6.set_xlim(self.x.min(), self.x.max())
        ax6.set_ylim(self.y.min(), self.y.max())
        ax6.set_zlim(self.z.min(), self.z.max())
        ax6.set_xlabel('X', color='white', fontsize=10)
        ax6.set_ylabel('Y', color='white', fontsize=10)
        ax6.set_zlabel('Z', color='white', fontsize=10)
        ax6.tick_params(colors='white', labelsize=8)
        ax6.set_title('动态轨迹生成', color='white', fontsize=12, pad=10)
        ax6.xaxis.pane.fill = False
        ax6.yaxis.pane.fill = False
        ax6.zaxis.pane.fill = False
        ax6.xaxis.pane.set_edgecolor('white')
        ax6.yaxis.pane.set_edgecolor('white')
        ax6.zaxis.pane.set_edgecolor('white')
        ax6.grid(True, alpha=0.2, linestyle=':', color='gray')

        # 动画更新函数
        def update(frame):
            idx = min(frame * 20, len(self.x) - 1)  # 加速动画
            line.set_data(self.x[:idx], self.y[:idx])
            line.set_3d_properties(self.z[:idx])

            point.set_data([self.x[idx]], [self.y[idx]])
            point.set_3d_properties([self.z[idx]])

            return line, point

        # 创建动画
        anim = FuncAnimation(fig, update, frames=range(0, len(self.x) // 20, 5),
                             interval=20, blit=True, repeat=True)

        # 参数说明
        param_text = f"参数: a={self.a}, b={self.b}, c={self.c}\n"
        param_text += f"步长: dt={self.dt}, 总步数: {self.steps}\n"
        param_text += f"模拟时间: {self.t[-1]:.1f} 单位\n"

        # 计算Lyapunov指数
        try:
            lyap_exp = self.calculate_lyapunov()
            param_text += f"最大Lyapunov指数(近似): {lyap_exp:.4f}\n"
            if lyap_exp > 0:
                param_text += "系统呈现混沌行为"
            else:
                param_text += "系统呈现周期性行为"
        except:
            param_text += "Lyapunov指数计算失败"

        fig.text(0.5, 0.02, param_text, ha='center', color='white', fontsize=10,
                 bbox=dict(boxstyle='round', facecolor='#1a1a1a', alpha=0.8))

        fig.suptitle('罗斯勒吸引子(Rössler Attractor)',
                     color='white', fontsize=14, y=0.98)

        plt.tight_layout()

        # 添加窗口大小变化事件处理器
        def on_resize(event):
            """窗口大小变化时自动调整布局"""
            plt.tight_layout()
            fig.canvas.draw_idle()

        fig.canvas.mpl_connect('resize_event', on_resize)

        # 保存动画
        if save_gif:
            try:
                from matplotlib.animation import PillowWriter
                writer = PillowWriter(fps=30)
                anim.save(filename, writer=writer)
                print(f"动画已保存为: {filename}")
            except Exception as e:
                print(f"保存动画失败: {e}")

        plt.show()
        return anim

    def explore_parameters(self):
        """探索不同参数对系统行为的影响（自动运行）"""
        # 定义要探索的参数组合
        param_sets = [
            (0.2, 0.2, 2.0, "周期轨道 (c=2.0)"),
            (0.2, 0.2, 3.5, "准周期轨道 (c=3.5)"),
            (0.2, 0.2, 5.7, "经典混沌 (c=5.7)"),
            (0.2, 0.2, 9.0, "高维混沌 (c=9.0)"),
            (0.1, 0.1, 14.0, "双涡卷结构"),
            (0.2, 0.1, 5.7, "非对称吸引子")
        ]

        fig, axes = plt.subplots(2, 3, figsize=(15, 10))
        fig.patch.set_facecolor('#0a0a0a')

        for idx, (a, b, c, title) in enumerate(param_sets):
            ax = axes[idx // 3, idx % 3]
            ax.set_facecolor('#0a0a0a')

            # 创建临时吸引子
            temp_attractor = RosslerAttractor(a=a, b=b, c=c, dt=0.01, steps=2000)
            temp_attractor.simulate(method='rk4')

            # 绘制
            colors = ['#00ffff', '#ff00ff', '#ffff00', '#00ff00', '#ff6600', '#ff00cc']
            ax.plot(temp_attractor.x, temp_attractor.y, lw=0.7, color=colors[idx], alpha=0.8)
            ax.set_xlabel('X', color='white', fontsize=9)
            ax.set_ylabel('Y', color='white', fontsize=9)
            ax.tick_params(colors='white', labelsize=7)
            ax.set_title(title, color='white', fontsize=10)
            ax.grid(True, alpha=0.1, linestyle=':', color='gray')

            # 添加参数文本
            param_text = f"a={a}, b={b}, c={c}"
            ax.text(0.05, 0.95, param_text, transform=ax.transAxes,
                    fontsize=8, color='white', verticalalignment='top',
                    bbox=dict(boxstyle='round', facecolor='#1a1a1a', alpha=0.7))

        fig.suptitle('参数探索: 不同参数对罗斯勒吸引子的影响', color='white', fontsize=14, y=0.95)
        plt.tight_layout()

        # 添加窗口大小变化事件处理器
        def on_resize(event):
            """窗口大小变化时自动调整布局"""
            plt.tight_layout()
            fig.canvas.draw_idle()

        fig.canvas.mpl_connect('resize_event', on_resize)

        plt.show()


def main():
    """主函数 - 演示罗斯勒吸引子的各种功能"""
    print("=" * 60)
    print("罗斯勒吸引子(Rössler Attractor)")
    print("=" * 60)

    # 1. 创建经典罗斯勒吸引子
    print("\n1. 创建经典罗斯勒吸引子 (a=0.2, b=0.2, c=5.7)...")
    rossler = RosslerAttractor(a=0.2, b=0.2, c=5.7, dt=0.01, steps=8000)

    # 2. 运行模拟
    print("2. 运行数值模拟(使用RK4方法)...")
    rossler.simulate(method='rk4')

    # 3. 计算Lyapunov指数
    print("3. 计算最大Lyapunov指数...")
    try:
        lyap_exp = rossler.calculate_lyapunov()
        print(f"   最大Lyapunov指数(近似值): {lyap_exp:.6f}")
        if lyap_exp > 0:
            print("   → 系统呈现混沌行为 (对初始条件敏感)")
        else:
            print("   → 系统呈现周期性行为")
    except Exception as e:
        print(f"   Lyapunov指数计算失败: {e}")

    # 4. 显示基本统计信息
    print("\n4. 轨迹统计信息:")
    print(f"   X范围: [{rossler.x.min():.2f}, {rossler.x.max():.2f}]")
    print(f"   Y范围: [{rossler.y.min():.2f}, {rossler.y.max():.2f}]")
    print(f"   Z范围: [{rossler.z.min():.2f}, {rossler.z.max():.2f}]")
    print(f"   模拟时间: {rossler.t[-1]:.1f} 单位")
    print(f"   总点数: {len(rossler.t)}")

    # 5. 创建并显示动画
    print("\n5. 创建可视化动画...")
    print("   注意: 这将打开一个包含6个子图的窗口")
    print("   - 左上: 3D轨迹图")
    print("   - 中上: XY平面投影")
    print("   - 右上: XZ平面投影")
    print("   - 左下: YZ平面投影")
    print("   - 中下: 时间序列")
    print("   - 右下: 动态轨迹生成")

    # 创建动画（不保存GIF，如需要保存可设置save_gif=True）
    anim = rossler.create_animation(save_gif=False, filename="rossler_attractor.gif")

    # 6. 自动运行参数探索
    print("\n6. 自动运行参数探索...")
    rossler.explore_parameters()

    print("\n" + "=" * 60)
    print("程序执行完成！")
    print("=" * 60)
    print("\n说明:")
    print("1. 如需保存动画，请在create_animation()中设置save_gif=True")
    print("2. 如需更改参数，可直接修改RosslerAttractor类的构造函数参数")
    print("3. 数值方法支持'euler'(欧拉法)和'rk4'(四阶龙格-库塔法)")
    print("4. 所有图形窗口关闭后程序将继续执行")


# 如果直接运行此文件，则执行主函数
if __name__ == "__main__":
    # 检查是否在Jupyter环境中
    try:
        from IPython import get_ipython

        in_jupyter = get_ipython() is not None
    except:
        in_jupyter = False

    if in_jupyter:
        print("检测到Jupyter环境，已禁用交互式输入")

    # 运行主程序
    main()
相关推荐
探序基因2 小时前
R语言-使用pheatmap函数画热图
开发语言·r语言
-凌凌漆-2 小时前
【JS】var与let的区别
开发语言·前端·javascript
码农三叔2 小时前
（7-3）自动驾驶中的动态环境路径重规划：实战案例：探险家的行进路线
人工智能·算法·机器学习·机器人·自动驾驶
ExiFengs2 小时前
Java使用策略模式实现多实体通用操作的优雅设计
java·开发语言·设计模式·策略模式
茶本无香2 小时前
设计模式之三—工厂模式：灵活对象创建的艺术
java·开发语言·设计模式·工厂模式
超级无敌大学霸2 小时前
c语言整型提升
c语言·开发语言
困惑阿三2 小时前
利用 Flexbox 实现无需媒体查询（Media Queries）的自动响应式网格。
开发语言·前端·javascript
曲幽2 小时前
FastAPI数据库实战：从SQLAlchemy原理到高效连接管理，告别性能瓶颈
python·sqlite·flask·fastapi·web·sqlalchemy·db
m0_748250032 小时前
C++ 预处理器
开发语言·c++
热门推荐
01GitHub 镜像站点02网站改了域名，如何查找？03Labelme从安装到标注：零基础完整指南04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06【踩坑笔记】50系显卡适配的 PyTorch 安装07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南082025-04-03 Latex学习1——本地配置Latex + VScode环境09Netlify 的深度解析及使用指南10电脑设置定时关机有多种方法(含python代码)