AI大模型-机器学习-算法-线性回归-优化方法

目的

为避免一学就会、一用就废，这里做下笔记

说明

• 本文紧承前文，欲渐进，请循序
• 本文讲述的优化方法，可能适用于模型训练的不同阶段，而非必须N选一，请注意区分
• 本文所述相关概念，在机器学习领域通用，线性回归只是它们的应用场景之一

优化方法

1、增加特征

目的 ：解决模型信息缺失问题

说明 ：

这是特征工程的一部分。如要预测房价 y y y，已知影响维度 [ x 1 , x 2 ] [x_1,x_2] [x1,x2]分别代表 [ [ [房屋面积、楼层 ] ] ]，仅这两个维度拟合出的效果并不好，可以增加 x 3 x_3 x3(是否有电梯)、 x 4 x_4 x4(地段评分)等其他影响房价的维度（因素）,让拟合结果 y y y更贴合现实。

优点：

1. 信息增益直接：引入全新的信息维度，可能直接解决模型的信息缺失问题
2. 可解释性强：新特征通常有明确的业务含义（如"是否有电梯"、"距离地铁站米数"）
3. 风险相对可控：每个特征的贡献相对独立，便于分析和调试
4. 避免过度变换：不会因为复杂变换而扭曲原始数据的物理意义

缺点：

1. 数据收集成本高：需要额外测量、调查或购买数据
2. 可能遗漏非线性关系：仅靠原始特征的线性组合可能无法捕捉复杂模式
3. 需要领域专业知识：要人为准确判断哪些新特征有价值，可能引入无关噪声

2、升维

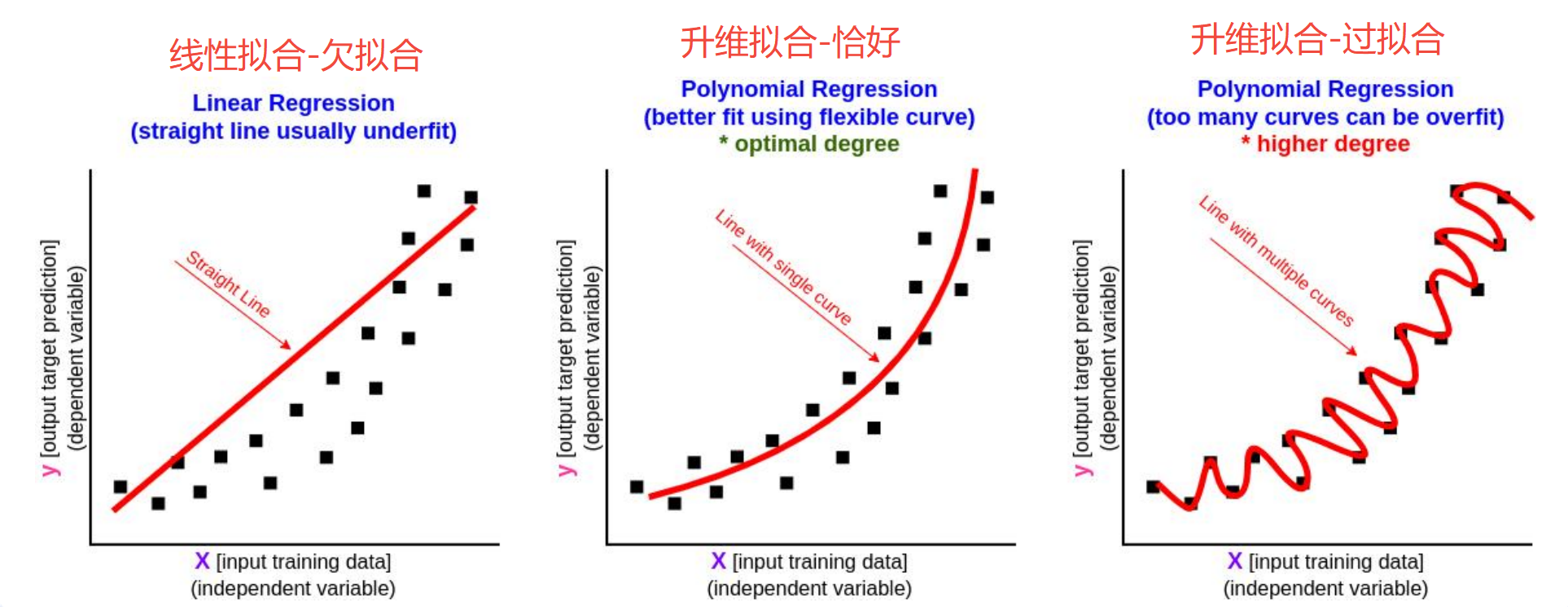
目的 ：解决输出和输入的非线性关系问题

说明 ：

和增加特征相似，升维也要增加维度，两者本质不同。升维中增加的维度，是从原始数据通过特征变换 得来。如物理公式 h = 1 2 g t 2 h= \frac{1}{2}gt^2 h=21gt2，结果 h h h和自变量 t t t之间是非线性关系，用传统的 y = a x + b y=ax+b y=ax+b线性函数无法正确拟合。但 h h h和 t 2 t^2 t2是线性关系，于是可以通过升维函数 Φ ( x ) Φ(x) Φ(x)来替代原变量，用线性回归的方法，拟合出 h h h和 Φ ( x ) Φ(x) Φ(x)的准确关系。

优点：

1. 无需额外数据：充分利用现有数据，挖掘深层信息
2. 能揭示非线性关系 ：通过多项式、交互项等捕捉特征间的复杂相互作用
   • 如：面积 × 单价 可能比单独的面积、单价更能预测总价
3. 可能发现潜在模式：变换后的特征可能在高维空间形成线性可分结构

缺点：

1. 维度爆炸风险 ：多项式扩展时，维度随阶数指数增长
   • 如：10个特征做3阶多项式 → 组合数可能超过100
2. 过拟合风险大：高维空间容易拟合噪声，尤其在小数据集上
3. 可解释性差 ：面积² 或 sin(时间) 的物理意义不如原始特征易理解
4. 计算成本高：高维特征需要更多内存和计算时间

3、降维

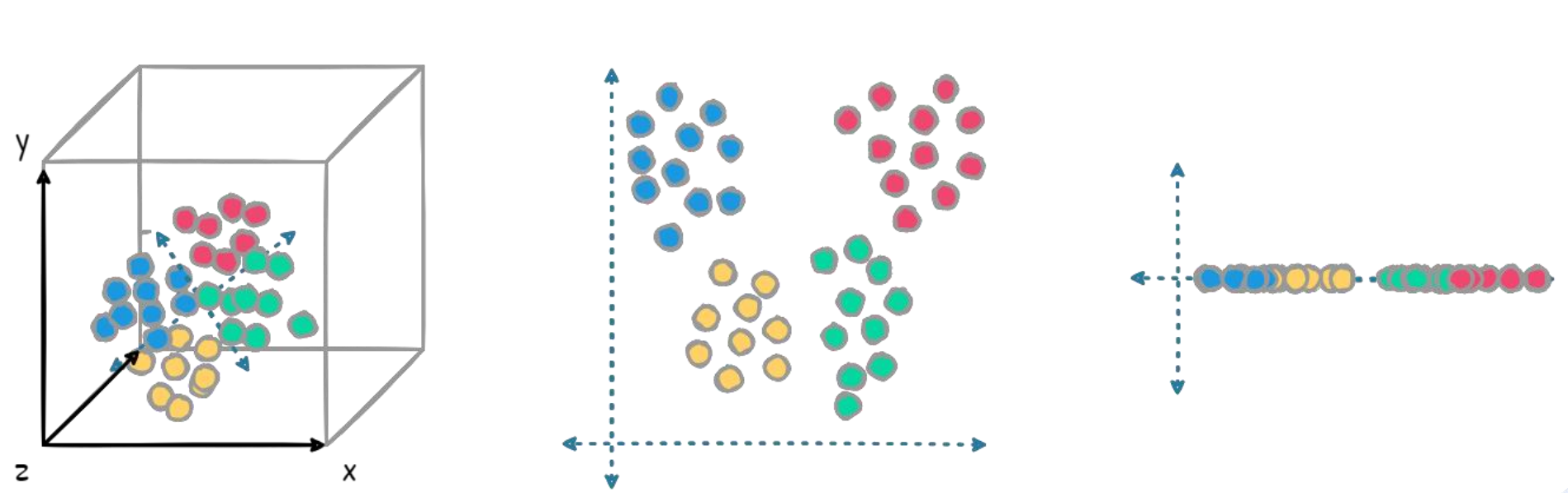
目的 ：解决高维数据的冗余、噪声和计算效率问题

说明 ：

降维是通过数学变换将高维特征映射到低维空间，同时尽可能保留原始数据的主要信息。当特征数量过多或存在多重共线性时，直接建模容易导致过拟合和计算困难。例如在图像识别中，每个像素可能都是特征，但相邻像素高度相关。通过降维方法（如PCA）可以提取主要成分，用少量不相关的新特征替代原始的高维特征。

优点：

1. 降低计算成本 ：减少特征数量，提升模型训练和预测速度
   • 如：将1000维图像特征压缩到50维
2. 去除噪声和冗余：保留数据的主要影响因素，过滤不重要的信息
3. 改善可视化：将高维数据降至2D/3D便于直观观察数据分布
4. 可能提升模型性能：消除多重共线性，减少过拟合风险

缺点：

1. 信息损失不可避免 ：低维表示无法100%保留原始信息，甚至可能丢失重要细节
   • 如：PCA保留95%，意味着接受5%的信息丢失
2. 可解释性下降：新特征（如"主成分1"）缺乏明确的物理含义
3. 方法选择依赖数据特性：不同降维方法（线性/非线性）适用于不同数据结构
4. 预处理步骤增加复杂度：需要额外调整降维参数（如保留维度数）

4、Early Stopping（提前停止）

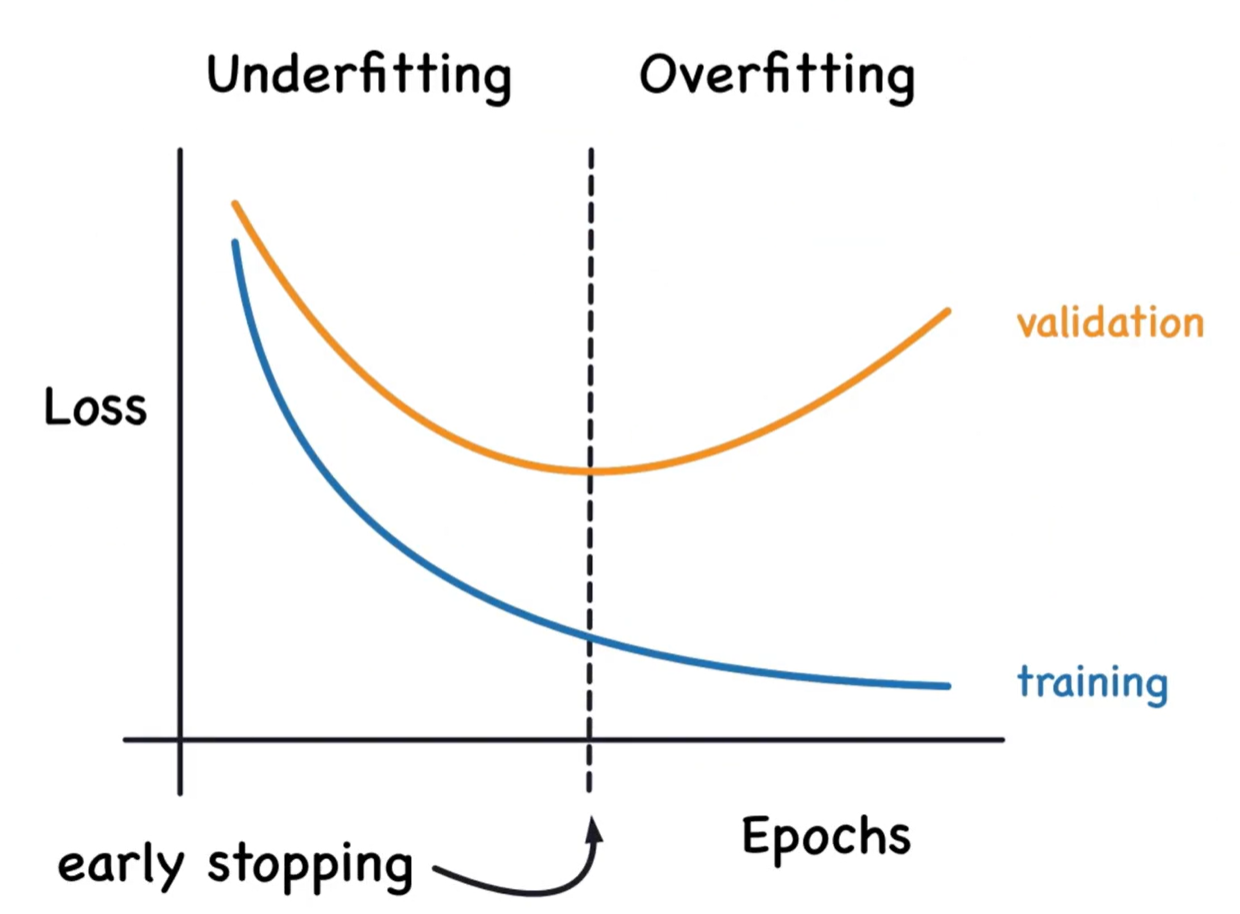
目的 ：解决训练过程中模型过拟合问题

说明 ：

Early Stopping是一种训练过程优化 技术，通过在模型开始过拟合之前停止训练来防止模型过度拟合训练数据 。

当使用迭代优化算法（如梯度下降）训练线性回归模型时，模型参数会随迭代次数增加而不断调整。在训练初期，模型同时在训练集和验证集上表现提升；但随着迭代继续，模型开始过度记忆训练数据中的噪声和细节，导致验证集性能下降。Early Stopping监控验证集误差，当连续多次迭代验证误差不再改善时自动停止训练。

优点：

1. 防止过拟合：在模型开始过度拟合噪声前停止，提高泛化能力
2. 节省训练时间：避免不必要的迭代，尤其在大数据集和复杂模型上显著减少计算成本
3. 自动确定最优迭代次数：无需手动调整训练轮数（epochs）超参数
4. 简单易实现：几乎所有深度学习框架都内置该功能，只需设置几个参数

缺点：

1. 需要验证集：必须从训练数据中划分出验证集，可能减少实际训练数据量
2. 可能提前停止：如果验证误差波动较大，可能错误地在模型还未充分学习时停止
3. 对验证集敏感：验证集的选择和大小会影响停止决策
4. 不适用于所有情况：当验证误差平台期较长时难以确定最佳停止点

5、正则化（惩罚项）

目的 ：解决过拟合和多重共线性问题

声明，这里的"正则 "二字，属于错误翻译，和常规理解的正则匹配完全无关，取"引入规则以纠正"的含义，相比而言，惩罚项一词更合适。

说明 ：

正则化（惩罚项）是在线性回归的损失函数中添加额外的约束项，通过对模型系数的大小进行惩罚来限制模型复杂度。普通线性回归最小化均方误差：
J ( θ ) = 1 2 m ∑ ( h θ ( x ( i ) ) − y ( i ) ) 2 J(θ) = \frac{1}{2m}∑(h_θ(x^{(i)}) - y^{(i)})^2 J(θ)=2m1∑(hθ(x(i))−y(i))2

而正则化版本最小化
J ( θ ) = 1 2 m ∑ ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ⋅ R ( θ ) J(θ) = \frac{1}{2m}∑(h_θ(x^{(i)}) - y^{(i)})^2 + λ·R(θ) J(θ)=2m1∑(hθ(x(i))−y(i))2+λ⋅R(θ)

其中 λ λ λ控制惩罚强度， R ( θ ) R(θ) R(θ)是惩罚函数。这迫使模型在拟合数据和控制系数大小之间寻找平衡。

优点：

1. 有效防止过拟合：通过限制系数大小，降低模型对噪声的敏感性
2. 处理多重共线性：当特征高度相关时，正则化能稳定解，避免系数爆炸
3. 特征选择能力：某些惩罚项（如L1）可将不重要特征的系数压缩为零
4. 提升模型稳定性：减小特征微小波动对预测的影响，增强鲁棒性
5. 适用于高维数据：在特征数多于样本数时仍能获得有效解

缺点：

1. 引入超参数λ：需要调整正则化强度，增加模型选择复杂度
2. 可能引入偏差：惩罚项会使系数向零收缩，可能引入系统性偏差
3. 损失可解释性：系数被压缩后，其大小不再直接反映特征重要性
4. 需要特征缩放：对特征的尺度敏感，使用前必须进行标准化
5. 计算成本增加：部分惩罚项（如L1）需要特殊优化算法

补充说明：常见惩罚项类型

类型	惩罚函数 R ( θ ) R(θ) R(θ)	特点	适用场景
L1正则化（LASSO）	∑ ∣ θ j ∣ ∑|θ_j| ∑∣θj∣	产生稀疏解，自动特征选择	特征数>样本数，需要特征选择
L2正则化（岭回归）	∑ θ j 2 ∑θ_j^2 ∑θj2	稳定解，系数平滑收缩	处理多重共线性，高相关特征
弹性网络	α ∑ ∣ θ j ∣ + ( 1 − α ) ∑ θ j 2 α∑|θ_j| + (1-α)∑θ_j^2 α∑∣θj∣+(1−α)∑θj2	L1和L2的折中，结合两者优点	既有相关特征又需要特征选择
提前停止	等效于自适应L2	通过训练过程控制复杂度	迭代优化算法

参数λ的影响

λ值过小 → 惩罚不足 → 接近普通线性回归 → 可能过拟合
λ值适中 → 偏差-方差平衡 → 最佳泛化性能
λ值过大 → 惩罚过强 → 系数被过度压缩 → 模型欠拟合

6、归一化

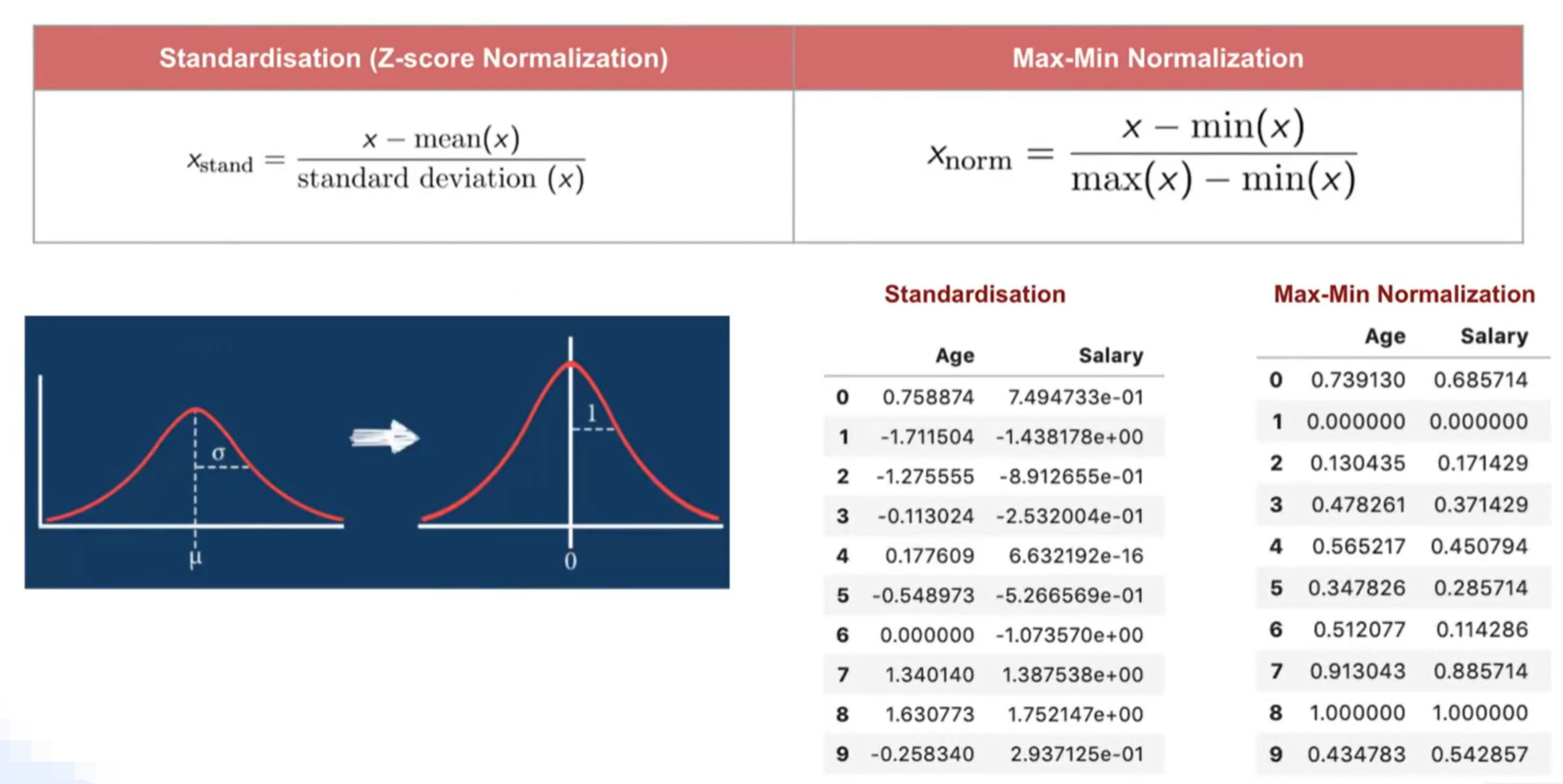
目的 ：解决特征尺度差异导致的优化问题

说明 ：

归一化是一种数据预处理 技术，通过对特征进行线性变换，使其数值范围在 [ 0 , 1 ] [0,1] [0,1]或数据符合正态分布。

这么做的原因是：当特征具有不同的量纲、尺度或取值范围时，直接用于线性回归会导致梯度下降收敛缓慢、系数解释困难、以及某些特征被过度加权的问题。归一化不改变数据的分布形状，但可将其映射到统一的数值范围。

优点：

1. 加速梯度下降收敛：所有特征在相似尺度上，梯度下降路径更直接
2. 公平对待所有特征：避免大数值特征主导模型，确保系数可比性
3. 改善正则化效果：让惩罚项对所有特征施加平等约束

缺点：

1. 可能丢失信息：最小-最大缩放对异常值敏感，可能压缩正常数据范围
2. 需要额外步骤：必须保存训练集的缩放参数，用于后续预测数据
3. 不适用于所有算法：树模型等基于排序的算法通常不需要归一化
4. 可能改变数据分布：某些归一化方法假设数据近似正态分布

补充说明：主要归一化方法对比

方法	公式	适用范围	特点
最小-最大归一化	x ′ = x − m i n ( x ) m a x ( x ) − m i n ( x ) x' = \frac{x - min(x)}{max(x)-min(x)} x′=max(x)−min(x)x−min(x)	数据有明确边界，如图像像素（0-255）	结果在[0,1]区间，对异常值敏感
Z-score标准化	x ′ = x − μ σ x' = \frac{x - μ}{σ} x′=σx−μ	数据近似正态分布	均值为0，标准差为1，更常用
Robust标准化	x ′ = x − m e d i a n I Q R x' = \frac{x - median}{IQR} x′=IQRx−median	数据包含异常值	使用中位数和四分位距，抗异常值
最大绝对值缩放	x ′ = x m a x ( ∣ x ∣ ) x' = \frac{x}{max(|x|)} x′=max(∣x∣)x	稀疏数据，已中心化数据	结果在[-1,1]区间

实践注意事项

1. 何时必须归一化：

   • 使用梯度下降优化时
   • 使用距离/相似度计算的算法（如KNN、SVM）
   • 应用正则化时
   • 使用PCA等依赖协方差的方法时

2. 何时可不归一化：

   • 树模型（决策树、随机森林）
   • 使用解析解（正规方程）求解线性回归时
   • 所有特征天然尺度相同时（如RGB颜色值）

3. 流程顺序：

   原始数据 → 划分训练/测试集 → 用训练集计算归一化参数 
         → 归一化训练集 → 用相同参数归一化测试集 → 建模

与其他优化手段的协同

归一化通常是预处理流水线的第一步：

1. 归一化 + 升维：先归一化原始特征，再进行多项式扩展
2. 归一化 + 正则化：确保惩罚项公平作用于所有特征
3. 归一化 + 降维：为PCA等提供尺度一致的特征输入
4. 归一化 + Early Stopping：加速收敛，使停止判断更可靠

核心价值 ：归一化不改变模型的数学本质，但通过优化数据表示 ，为后续所有建模步骤创造公平、稳定的数值环境，是工业级机器学习流水线中几乎必需的预处理步骤。