【洛谷】分治专题 逆序对、第 k 小、最大子段和

文章目录

• 逆序对
• 求第k小的数
• 最大子段和

---

分治，字⾯上的解释是「分⽽治之」，就是把⼀个复杂的问题分成两个或更多的相同或相似的⼦问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

因为分治也是把复杂的问题拆分成相似的子问题，所以分治也通常用递归实现。

逆序对

题目描述

题目解析

本题是一道利用分治思想解决的典型例题，代码核心结构和归并排序很像，并且统计逆序对个数本身也需要序列有序。

子问题拆分就是拿到一个区间，先将区间分成左右区间，然后各自求左右区间的逆序对个数，在求左右区间的逆序对个数的同时利用归并排序将左右区间排成有序，最后再求有序的左右区间之间的逆序对个数：思路是用两个指针cur1、cur2分别指向left和mid+1，依次扫描左右区间一遍，逆序对是算左区间比右区间大的一对数，当a[cur1] > a[cur2]时，说明此时左区间的最小值都比a[cur2]大，说明右区间中a[cur1]及a[cur1]右边的元素都满足比a[cur2]大，所以需要ret += mid - cur1 + 1，然后进行归并排序，将较小的a[cur2]放到临时数组t中，当a[cur1] <= a[cur2]时，只需完成归并排序操作即可。 归根结底求逆序对就只在a[cur1] > a[cur2]时多了一个计算ret的操作，在多了一个递归需要返回ret的操作。
注意：

1、本题逆序对个数ret需要用long long类型，因为数据范围是5e5，最坏可能是序列整体递减，以 5 4 3 2 1为例，以5为基准右4对，以4为基准有3对...，本质就是等差数列求和（1 + 5e5 - 1） * （5e5 - 1） / 2。（首项加末项乘项数除二）

2、本题对序列进行排序不会影响最终结果，因为在对一个区间排序之前已经完成了对左右区间的各自的逆序对统计工作，体现在代码中就是递归函数首先merge左右区间，merge会先分别统计左右区间的逆序对个数，然后再分别对左右区间进行排序，出了merge左右区间后再统计左右区间之间的逆序对个数。
特别补充：小编关于写递归代码的一点小思考：

递归函数可以想像成一个链表，链表有它的前驱结点和后继结点，就可以类比成递归函数的前提条件和递归函数执行后会产生的结果，对于这道题来说前提条件就是左右区间需要有序，所以递归函数内部需要实现将区间排序的操作，递归函数执行后的结果是算出这段区间的逆序对数目，所以递归函数内部需要计算ret值。

代码

#include <iostream>
using namespace std;

typedef long long LL;

const int N = 5e5 + 10;
int a[N]; //存储原始数据的数组
int t[N]; //供归并排序的临时数组

LL merge(int left, int right)
{
	if (left >= right)
		return 0;

	LL ret = 0;
	int mid = (left + right) / 2;
	//分别统计左右区间各自的逆序对个数
	ret += merge(left, mid);
	ret += merge(mid + 1, right);
	//左右区间merge完后已经有序，下面可以统计左右区间之间的逆序对个数了

	//借助归并排序思路将两区间排序并统计左右区间的逆序对个数
	int pv = left, cur1 = left, cur2 = mid + 1;
	//找左区间中比右区间大的值
	while (cur1 <= mid && cur2 <= right)
	{
		if (a[cur1] > a[cur2])
		{
			//若右区间最小值都比a[cur1]大，那么cur1及右边元素全部符合
			ret += mid - cur1 + 1;
			t[pv++] = a[cur2++];
		}
		else
		{
			t[pv++] = a[cur1++];
		}
	}

	//处理剩余元素
	while(cur1 <= mid)
		t[pv++] = a[cur1++];
	while (cur2 <= right)
		t[pv++] = a[cur2++];

	//将排序好的序列放回原数组
	for (int i = left; i <= right; i++)
	{
		a[i] = t[i];
	}

	return ret;
}

int main()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	cout << merge(1, n) << endl;
	return 0;
}

求第k小的数

题目描述

题目解析

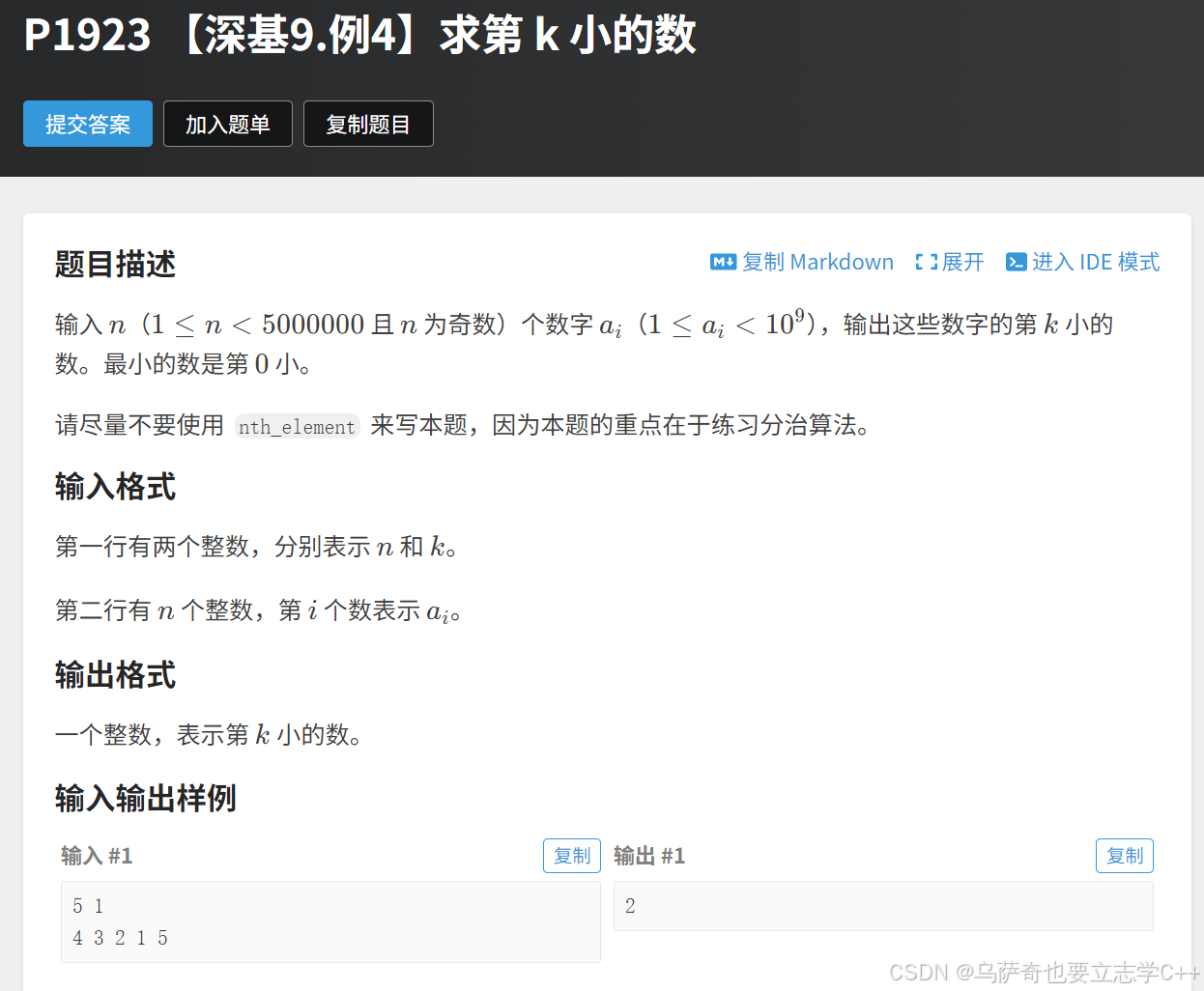
类似题我们在讲堆时有介绍，找序列中的第k小的数核心思路就是维护一个大小为k的大根堆（本题最小的数是第0小所以堆的大小是k+1），堆顶是数即为序列第k小。

本题小编介绍一个效率更高的解法，利用快速选择算法，该算法是基于快排实现的。
本题递归函数代码的前半部分完全就是快排的代码。当利用快排将数组分三块后我们需要统计每一块数组的元素个数，用来判断第k小在数组那一块，假设左区间[left, l]的元素个数为a，中间区间[l + 1, r - 1]的元素个数为b，右区间[l, right]的元素个数为c，如果k <= a说明第k小在左区间，需要继续递归左区间，如果k <= a + b说明第k小在中间区间，因为中间区间值全是基准值p，所以直接返回p，其余情况第k小在右区间，继续递归右区间。因为我们只对存在答案的区间进行递归，所以本题代码的效率会比快排的效率更高。

递归出口即left == right，这时该区间只有一个元素，因为经过前面的代码锁定，我们要找的第k小一定在这个区间，所以该区间的唯一元素e[left]即为总终答案，直接递归返回e[left]。

代码

注意由于本题数据规模很大，输入输出应将cin和cout换为scanf和printf。

#include <ctime>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 5e6 + 10;
int e[N];
int n, k;

int getrandom(int left, int right)
{
	return e[rand() % (right - left + 1) + left];
}

int qselect(int left, int right, int k)
{
	if (left == right)
		return e[left];  //重合即为答案

	//选择基准值
	int p = getrandom(left, right);
	//数组分三块
	int i = left, l = left - 1, r = right + 1;
	while(i < r)
	{
		if (e[i] < p)
		{
			swap(e[++l], e[i++]);
		}
		else if (e[i] == p)
		{
			i++;
		}
		else
		{
			swap(e[--r], e[i]);
		}
	}
	//统计三个区间元素个数
	//[left, l] [l + 1. r - 1] [r, right]
	int a = l - left + 1; //左区间
	int	b = r - l - 1; //中间区间
	int	c = right - r + 1; //右区间
	//选择存在最终结果的区间
	if (k <= a)
	{
		//第k小在左区间
		return qselect(left, l, k);
	}
	else if (k <= a + b)
	{
		//第k小在中间区间
		return p; // ?
	}
	else
	{
		//第k小在右区间
		return qselect(r, right, k - a - b);
	}
}

int main()
{
	srand(time(0));

	scanf("%d %d", &n, &k);
	k++; //因为本题从第0小开始，所以需要k++
	//初始化原数组
	for (int i = 1; i <= n; i++)
	{
		scanf("%d", &e[i]);
	}
	//快速选择算法
	int ret = qselect(1, n, k);
	printf("%d\n", ret);
	return 0;
}

最大子段和

题目描述

题目解析

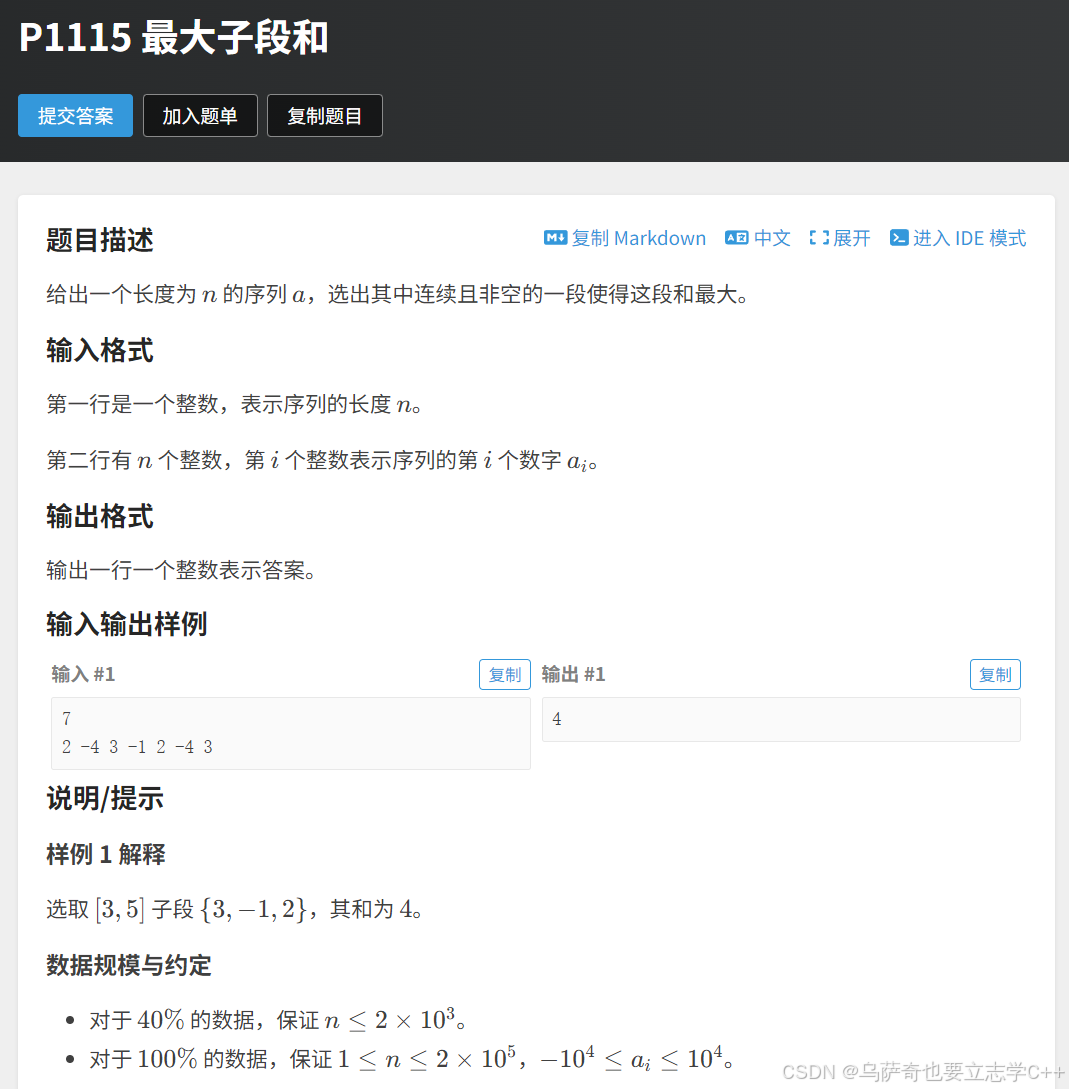
本题我们在前缀和和贪心专题都接触过，这里我们再利用分治解决一下。

分治首先将区间一分为二，我们需要分别计算左区间、右区间、横跨左右区间的最大子段和，然后求它们三者的最大值既为最大子段和。

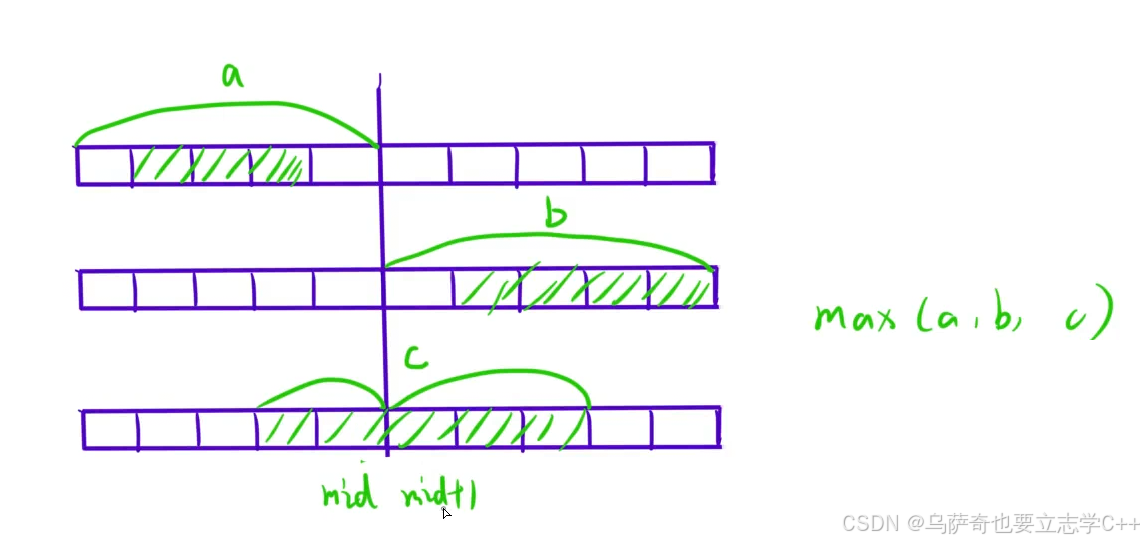
左区间和右区间的最大子段和我们利用递归dfs计算（dfs具体如何计算我们不关心，我们只用相信它一定能帮助我们计算出正确答案即可）。

然后计算横跨左右区间的最大子段和，需要分别计算以mid为右端点的区间的最大子段和lmax和以mid+1为左端点的区间的最大子段和rmax，横跨左右区间的最大子段和即为lmax + rmax。我们以左区间为例，我们需要分别计算区间[mid, mid] [mid - 1, mid] ... [left, mid]的子段和，并统计出横跨左右区间中的左子区间的最大字段和。
代码

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 2e5 + 10;
int a[N];

int dfs(int left, int right)
{
	if (left >= right)
		return a[left];

	//中间结点
	int mid = (left + right) / 2;
	//分别求左区间、右区间最大子段和
	int ret = max(dfs(left, mid), dfs(mid + 1, right));

	//求横跨左右区间的最大子段和
	int lsum = a[mid], lmax = a[mid];
	for (int i = mid - 1; i >= left; i--)
	{
		lsum += a[i];
		lmax = max(lmax, lsum);
	}

	int rsum = a[mid + 1], rmax = a[mid + 1];
	for (int i = mid + 2; i <= right; i++)
	{
		rsum += a[i];
		rmax = max(rmax, rsum);
	}

	ret = max(ret, lmax + rmax);
	return ret;
}

int main()
{
	int n;
	cin >> n;
	//初始化
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}

	cout << dfs(1, n) << endl;
	return 0;
}

以上就是小编分享的全部内容了，如果觉得不错还请留下免费的关注和收藏
如果有建议欢迎通过评论区或私信留言，感谢您的大力支持。
一键三连好运连连哦~~