一、研究背景
该代码面向回归预测 任务,结合了TCN(时间卷积网络) 与 Transformer 的优势,并引入遗传算法(GA) 进行超参数优化,旨在提升模型在复杂数据中的预测精度与泛化能力。
二、主要功能
- 数据预处理:归一化、训练集/测试集划分。
- 超参数优化:使用 GA 优化 TCN 的卷积核数、卷积核大小、丢弃率、层数及 Transformer 注意力头数。
- 模型构建与训练:构建 TCN-Transformer 混合网络并进行训练。
- 预测与评估:对训练集和测试集进行预测,计算 RMSE、R²、MAE 等指标。
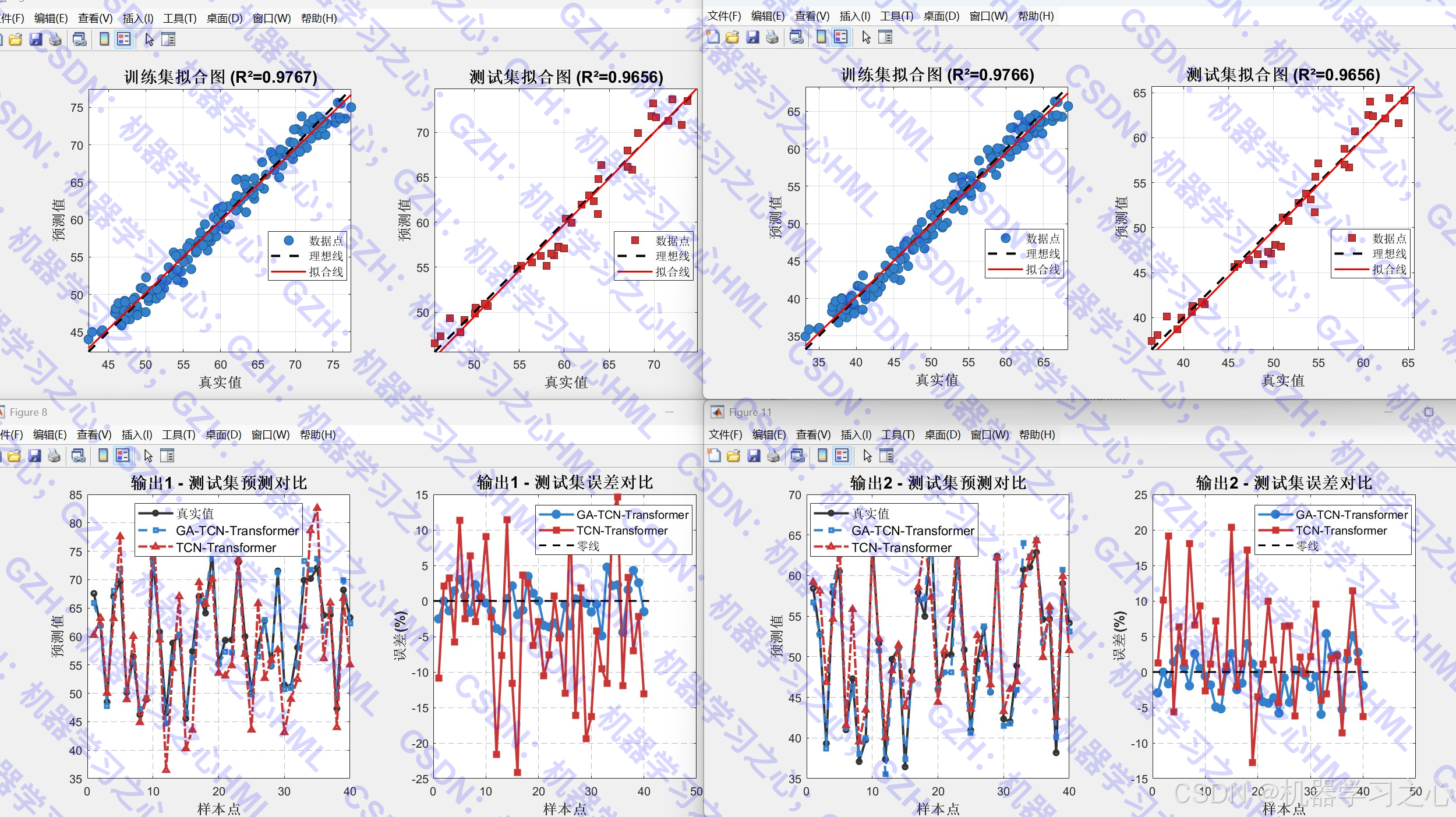
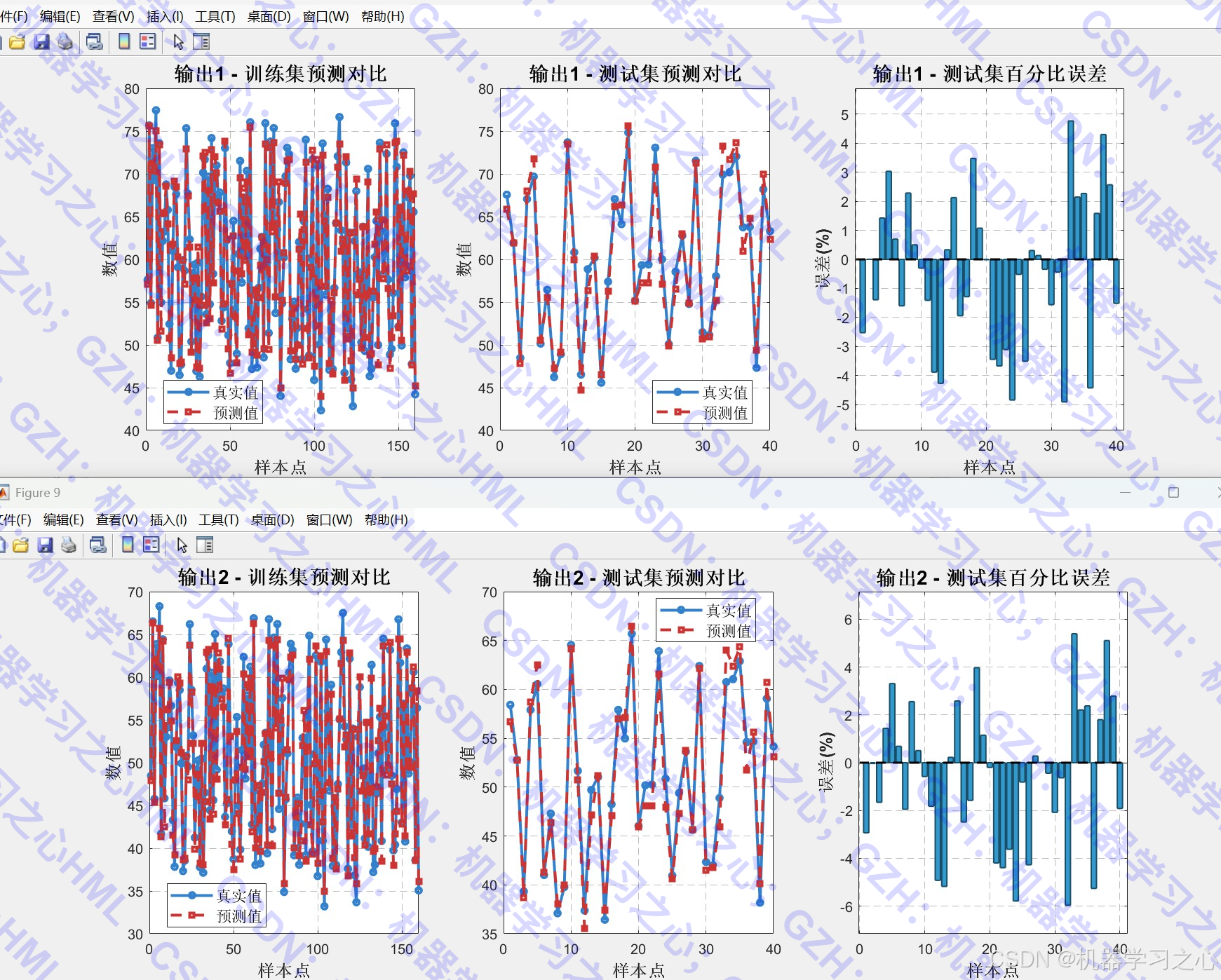
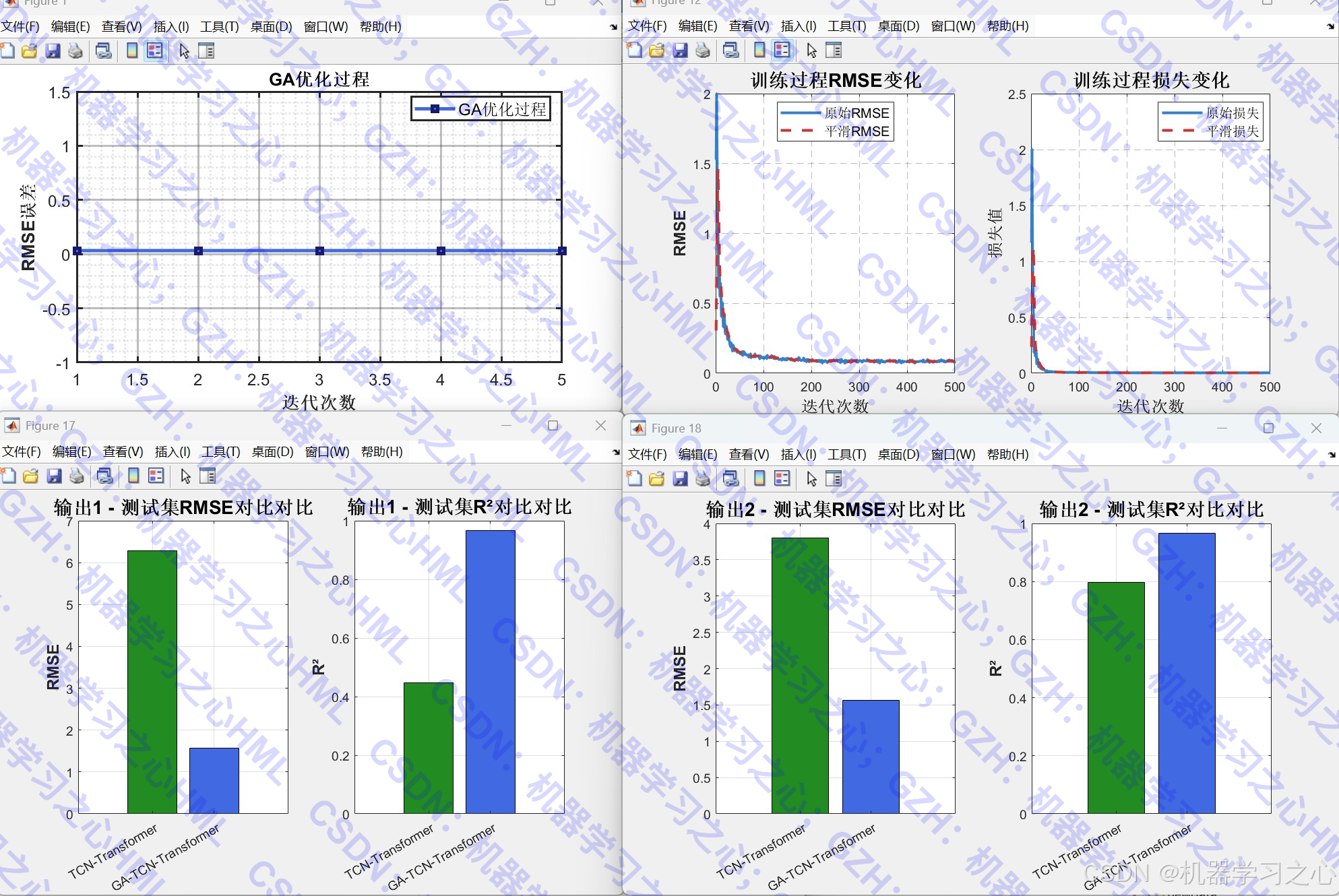
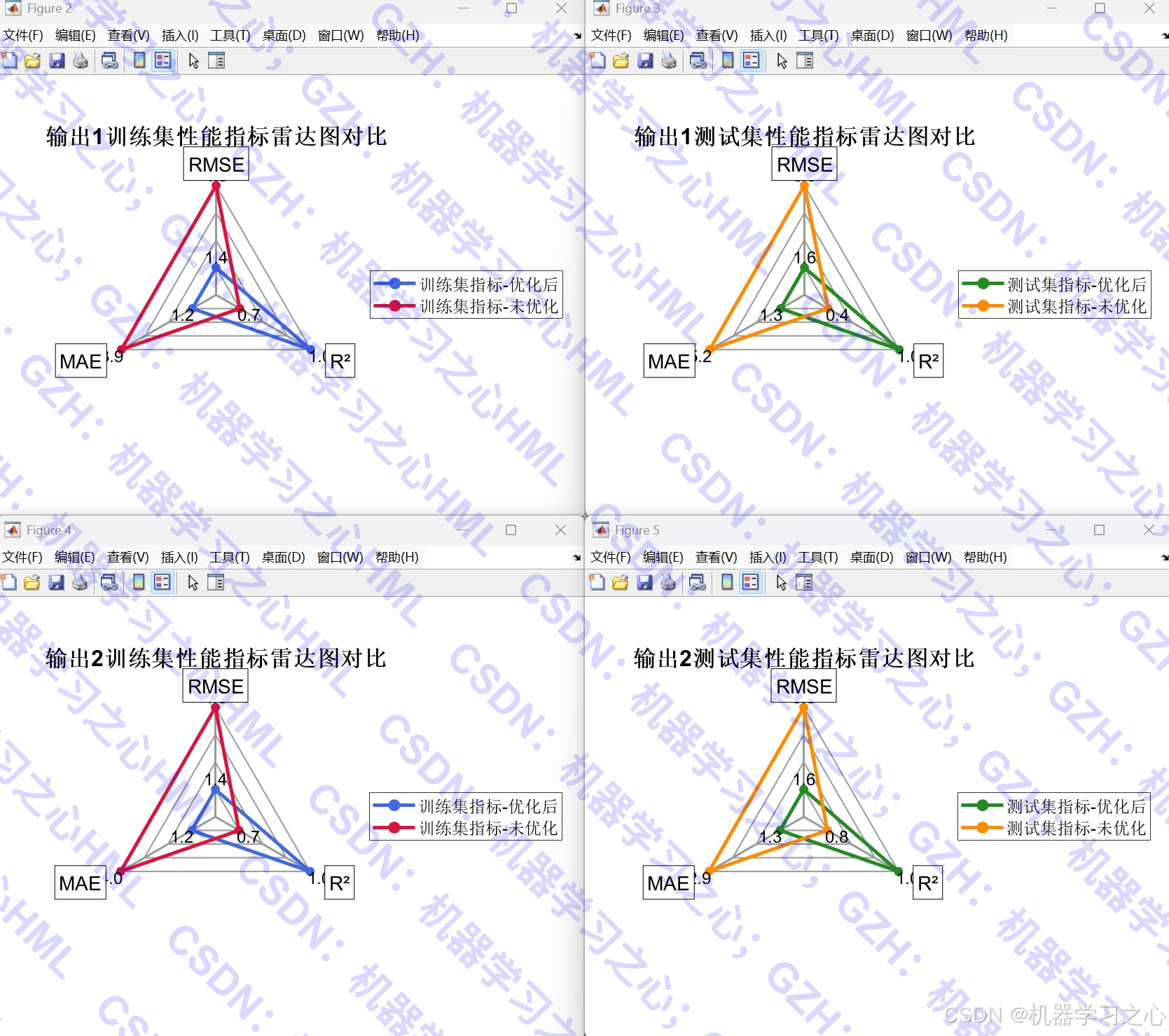
- 结果可视化:包括优化过程曲线、预测对比图、拟合图、雷达图、误差分析图等。
- 新数据预测:支持导入新数据进行预测并保存结果。
三、算法步骤
- 导入数据并归一化。
- 划分训练集与测试集(可选是否打乱样本)。
- 定义 GA 优化目标函数,优化 TCN-Transformer 超参数。
- 使用最优参数构建 TCN-Transformer 网络。
- 训练网络并评估性能。
- 进行预测并反归一化。
- 计算多项评估指标并可视化对比。
- 对新数据进行预测并输出结果。
四、技术路线
- 数据流:原始数据 → 归一化 → GA 优化 → 网络构建 → 训练 → 预测 → 反归一化 → 评估。
- 模型结构 :
- TCN 部分:多层因果卷积 + 残差连接 + 层归一化 + Dropout。
- Transformer 部分:位置编码 + 自注意力层 + 全连接输出。
- 优化方法:遗传算法(GA)用于超参数搜索,目标函数为 RMSE。
五、公式原理(简要)
- TCN:使用因果卷积确保时序因果性,膨胀卷积扩大感受野。
- Transformer:自注意力机制捕捉全局依赖关系。
- GA:模拟自然选择过程,通过选择、交叉、变异寻找最优解。
- 评估指标 :
- RMSE = 1n∑i=1n(yi−y^i)2\sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}n1∑i=1n(yi−y^i)2
- R² = 1−∑(yi−y^i)2∑(yi−yˉ)21 - \frac{\sum(y_i - \hat{y}_i)^2}{\sum(y_i - \bar{y})^2}1−∑(yi−yˉ)2∑(yi−y^i)2
- MAE = 1n∑∣yi−y^i∣\frac{1}{n}\sum|y_i - \hat{y}_i|n1∑∣yi−y^i∣
六、参数设定
- GA参数:种群数 N=8,迭代次数 Max_iteration=5。
- TCN参数范围 :
- 卷积核数:232^323 到 272^727(8~128)
- 卷积核大小:3~9
- 丢弃率:0.001~0.5
- TCN层数:2~5
- Transformer参数范围:注意力头数 2~6。
- 训练参数:Adam优化器,初始学习率 0.01,最大迭代 500 轮。
七、运行环境
- 平台:MATLAB2024b(需安装深度学习工具箱、优化工具箱)。
八、应用场景
- 风速预测
- 交通流量预测
- 股票价格预测
- 电力负荷预测
- 工业过程参数预测