一、深度学习的起伏发展史:从感知机到ImageNet革命
深度学习的演进并非一帆风顺,它经历了两次寒冬与三次复兴,每一次技术突破都推动着行业向前跨越。
1. 萌芽期:感知机的诞生与局限(1950s-1960s)
- 1958年 :Frank Rosenblatt提出感知机(Perceptron),这是第一个具有学习能力的人工神经网络模型。它本质是一个线性分类器,通过调整权重来学习输入与输出的映射关系,被视为神经网络的雏形。
- 1969年:Marvin Minsky和Seymour Papert在《Perceptrons》一书中指出,感知机无法解决"异或(XOR)"这类非线性问题,且无法扩展到多层结构。这一结论直接导致神经网络研究陷入近十年的"第一次寒冬"。
2. 复苏期:多层网络与反向传播(1980s)
- 1980年:**多层感知机(Multi-layer Perceptron, MLP)**被提出,通过引入隐藏层来处理非线性问题。从结构上看,它与现代深度神经网络(DNN)已非常相似,但受限于计算能力和训练数据,当时并未展现出优势。
- 1986年:David Rumelhart等人重新发明了**反向传播(Backpropagation)**算法,通过链式法则计算梯度,实现了对多层网络的有效训练。不过当时的研究发现,当隐藏层超过3层时,模型性能提升并不明显,甚至会出现梯度消失问题,深层网络的价值仍未被充分验证。
- 1989年:学界提出"单隐藏层已足够逼近任意连续函数"的论断,引发了"为何需要深度网络"的广泛质疑,深度学习进入"第二次寒冬"。
3. 爆发期:算力突破与数据驱动(2000s-2010s)
- 2006年:Geoffrey Hinton提出用**受限玻尔兹曼机(Restricted Boltzmann Machine, RBM)**初始化深层网络,有效缓解了梯度消失问题,为深层网络的训练提供了可行方案,这被视为深度学习复兴的起点。
- 2009年:GPU开始被用于加速深度学习计算。相比CPU,GPU的并行计算能力可将训练速度提升数十倍,彻底打破了深层网络的算力瓶颈。
- 2011年:深度学习在语音识别领域取得重大突破,微软、谷歌等公司将其应用于产品中,识别准确率大幅提升,标志着技术开始从实验室走向产业落地。
- 2012年:Alex Krizhevsky团队的AlexNet模型在ImageNet图像识别竞赛中夺冠,错误率从26%降至15.3%,远超传统方法。这一事件彻底引爆了全球对深度学习的关注,开启了人工智能的"黄金十年"。
📌 配图1:深度学习发展时间线图表

二、深度学习的核心三步法:从函数集合到最优模型
深度学习的本质是一个"函数筛选"的过程,通过三步即可构建出强大的预测模型,其底层逻辑简洁而深刻。
1. Step 1:定义函数集合------神经网络的设计
深度学习的函数集合由**神经网络(Neural Network)**来定义,而神经网络的核心是神经元与连接方式。
- 神经元(Neuron) :模拟生物神经元的工作原理,输入信号通过权重加权求和,加上偏置后经过激活函数(如Sigmoid、ReLU)输出非线性结果。例如Sigmoid函数:
σ(z)=11+e−z\sigma(z) = \frac{1}{1+e^{-z}}σ(z)=1+e−z1
它将输入映射到(0,1)区间,常用于二分类任务的输出层。 - 网络结构 :不同的神经元连接方式形成不同的网络结构,常见的有:
- 全连接前馈网络(Fully Connected Feedforward Network):每一层的神经元与下一层的所有神经元相连,是最基础的网络结构。
- 卷积神经网络(CNN):通过局部连接和权值共享,有效处理图像等网格状数据。
- 循环神经网络(RNN):通过记忆机制处理序列数据(如文本、语音)。
- 网络参数θ\boldsymbol{\theta}θ:包含所有神经元的权重(weights)和偏置(biases),参数的数量决定了模型的复杂度和拟合能力。
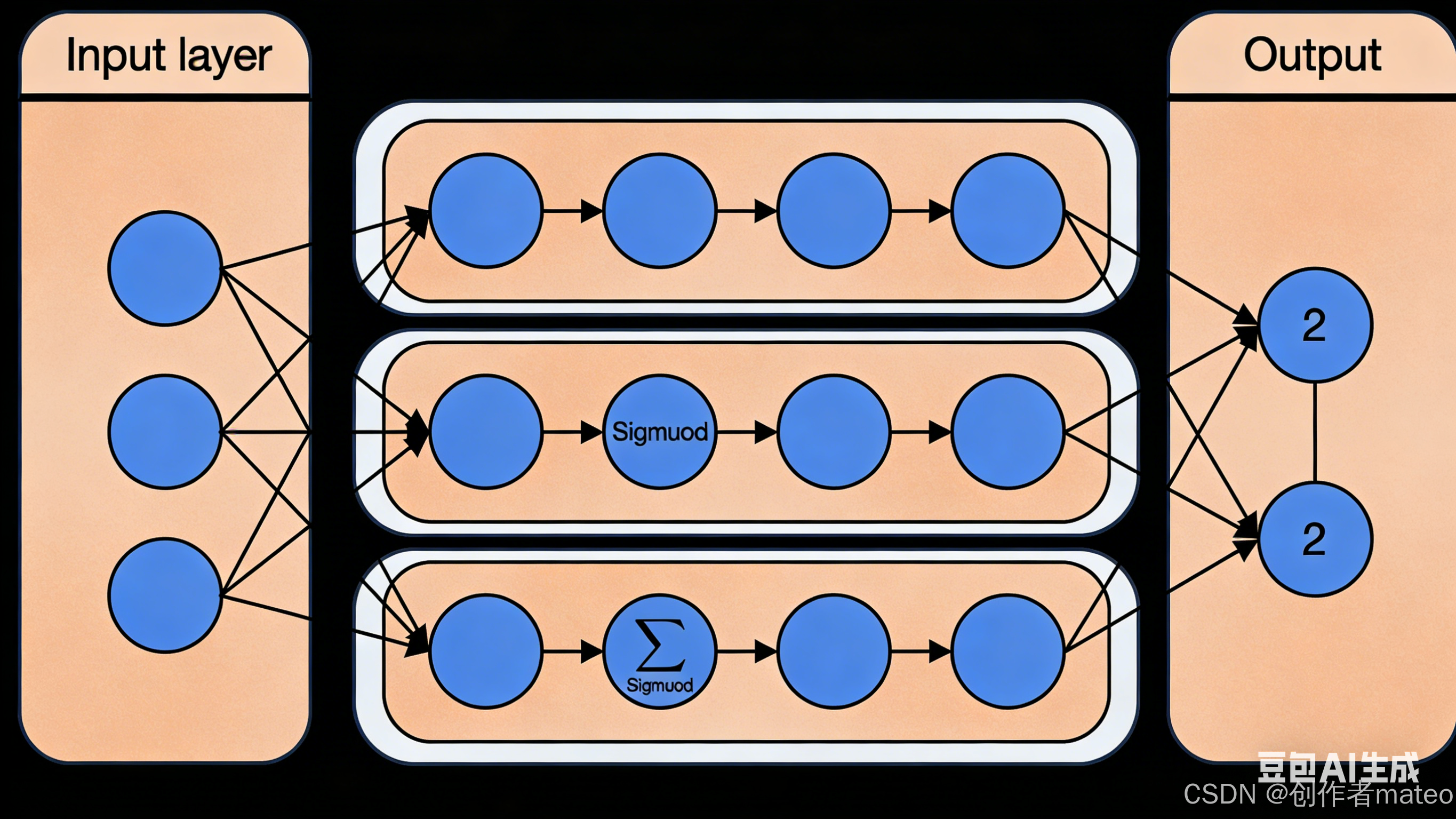
📌 配图2:多层感知机(MLP)结构示意图
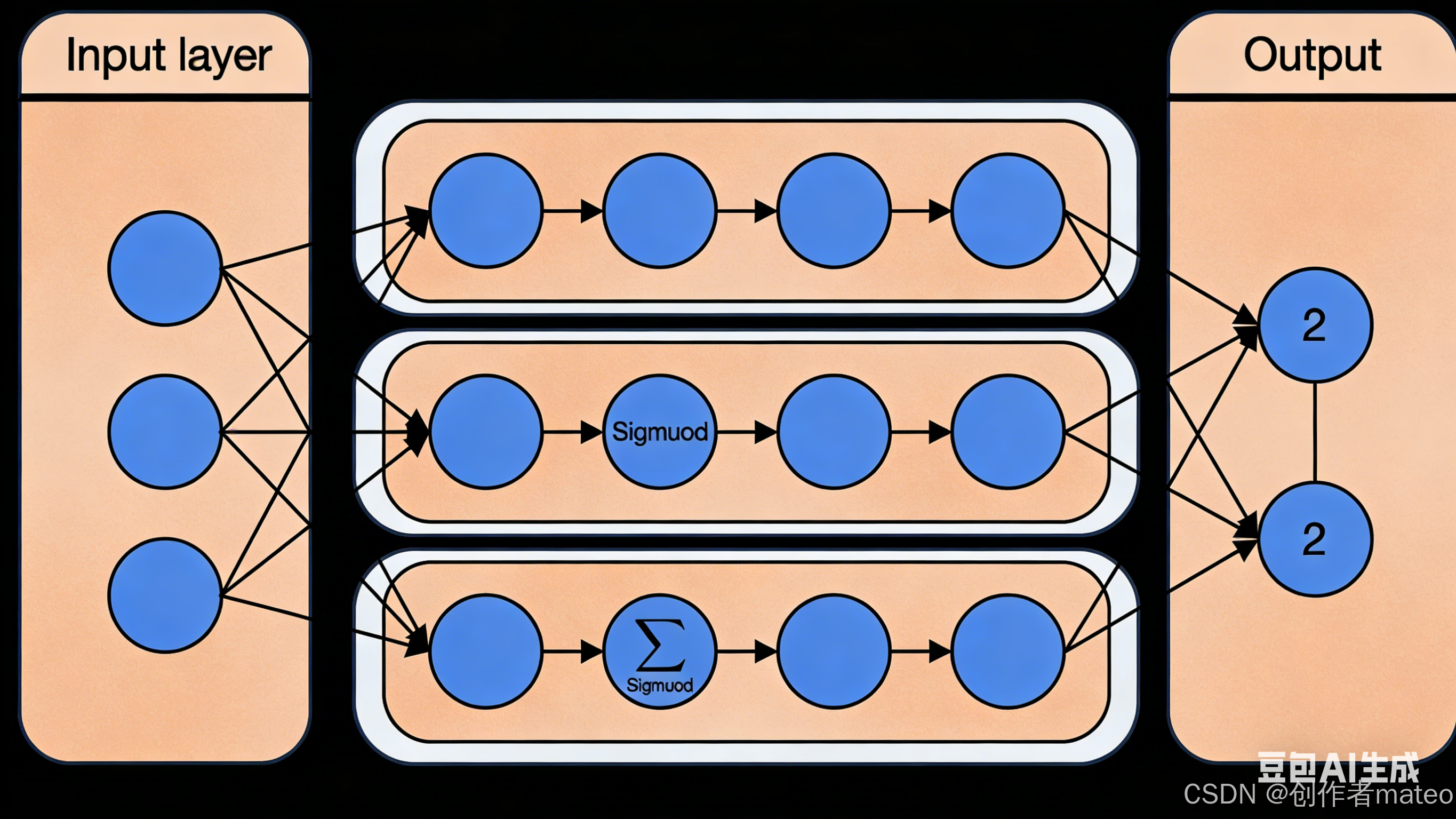
2. Step 2:评估函数优劣------损失函数的选择
损失函数(Loss Function)用于衡量模型预测值与真实标签的差距,是评估函数好坏的核心指标。
- 多分类任务 :常用交叉熵损失(Cross-Entropy Loss) ,公式为:
C(y,y^)=−∑i=1ny^ilnyiC(y,\hat{y}) = -\sum_{i=1}^{n}\hat{y}_i\ln y_iC(y,y^)=−i=1∑ny^ilnyi
其中yiy_iyi是模型对第iii类的预测概率,y^i\hat{y}_iy^i是真实标签(one-hot编码)。交叉熵越小,说明预测结果越接近真实值。 - 回归任务 :常用均方误差(MSE) ,公式为:
MSE(y,y^)=1n∑i=1n(yi−y^i)2MSE(y,\hat{y}) = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2MSE(y,y^)=n1i=1∑n(yi−y^i)2
衡量预测值与真实值的平均平方差。
3. Step 3:选择最优函数------梯度下降与优化
在定义好函数集合和损失函数后,我们需要通过优化算法找到使损失最小的函数,**梯度下降(Gradient Descent)**是最核心的优化方法。
- 梯度下降原理 :计算损失函数对每个参数的梯度,沿着梯度负方向更新参数,逐步逼近最优解。参数更新公式为:
θt+1=θt−α⋅∇C(θt)\theta_{t+1} = \theta_t - \alpha \cdot \nabla C(\theta_t)θt+1=θt−α⋅∇C(θt)
其中α\alphaα是学习率(Learning Rate),控制每一步更新的幅度。 - 进阶优化算法:为了提升训练效率和稳定性,衍生出了动量(Momentum)、Adam、RMSProp等优化器,它们通过自适应调整学习率或引入动量机制,加速收敛并避免局部最优。
📌 配图3:反向传播算法流程图
三、神经网络的计算原理:矩阵运算与并行加速
神经网络的前向传播和反向传播本质上是矩阵运算的过程,而GPU的并行计算能力正是深度学习得以高效运行的关键。
1. 前向传播:从输入到输出的映射
以全连接网络为例,前向传播的计算过程可表示为:
z(l)=W(l)a(l−1)+b(l)z^{(l)} = W^{(l)}a^{(l-1)} + b^{(l)}z(l)=W(l)a(l−1)+b(l)
a(l)=σ(z(l))a^{(l)} = \sigma(z^{(l)})a(l)=σ(z(l))
其中W(l)W^{(l)}W(l)是第lll层的权重矩阵,b(l)b^{(l)}b(l)是偏置向量,a(l)a^{(l)}a(l)是第lll层的激活输出,σ\sigmaσ是激活函数。
通过矩阵乘法,我们可以高效地计算每一层的输出,最终得到模型的预测结果y=f(x)y = f(x)y=f(x)。
2. 反向传播:梯度的链式法则
反向传播通过链式法则计算损失函数对各层参数的梯度,核心步骤为:
- 计算输出层的误差:δ(L)=∂C∂z(L)\delta^{(L)} = \frac{\partial C}{\partial z^{(L)}}δ(L)=∂z(L)∂C
- 反向传播误差:δ(l)=(W(l+1)Tδ(l+1))⊙σ′(z(l))\delta^{(l)} = (W^{(l+1)T}\delta^{(l+1)}) \odot \sigma'(z^{(l)})δ(l)=(W(l+1)Tδ(l+1))⊙σ′(z(l))
- 计算参数梯度:∂C∂W(l)=δ(l)a(l−1)T\frac{\partial C}{\partial W^{(l)}} = \delta^{(l)}a^{(l-1)T}∂W(l)∂C=δ(l)a(l−1)T,∂C∂b(l)=δ(l)\frac{\partial C}{\partial b^{(l)}} = \delta^{(l)}∂b(l)∂C=δ(l)
其中⊙\odot⊙表示逐元素相乘,σ′\sigma'σ′是激活函数的导数。
3. GPU加速的核心价值
CPU的核心数量较少,擅长串行计算;而GPU拥有数千个流处理器,擅长并行处理大规模矩阵运算。例如,在训练AlexNet时,使用GPU可将训练时间从数周缩短至数天,这一突破直接推动了深层网络的广泛应用。
📌 配图4:GPU与CPU并行计算对比示意图

四、实践中的关键问题与挑战
深度学习在理论上已非常成熟,但在工程实践中仍面临诸多挑战,以下是最常见的问题:
1. 网络结构设计:层数与神经元数量的选择
这是深度学习中最具经验性的问题,没有固定公式可遵循,需结合任务场景和数据规模进行调优:
- 层数选择:简单任务(如MNIST手写数字识别)使用2-3层即可,复杂任务(如ImageNet图像分类)则需要更深的网络(如ResNet-50有50层)。
- 神经元数量:每层神经元数量通常在几十到几千之间,过多易导致过拟合,过少则可能欠拟合。一般遵循"输入层→隐藏层逐渐减少→输出层匹配任务需求"的原则。
2. 过拟合与正则化
当模型在训练集上表现良好但在测试集上表现较差时,就发生了过拟合。常用的解决方法包括:
- Dropout:训练时随机丢弃部分神经元,减少神经元间的共适应,增强模型泛化能力。
- L1/L2正则化:在损失函数中加入参数的L1或L2范数惩罚,限制参数的大小,防止模型过于复杂。
- 数据增强:通过旋转、裁剪、翻转等方式扩充训练数据,提升模型的鲁棒性。
3. 梯度消失与爆炸
在深层网络中,梯度在反向传播时可能会指数级衰减(梯度消失)或增长(梯度爆炸),导致模型无法收敛。解决方法包括:
- 使用ReLU激活函数:ReLU的导数在正区间恒为1,有效缓解梯度消失问题。
- 权重初始化:使用He初始化、Xavier初始化等方法,使各层的输出方差保持一致。
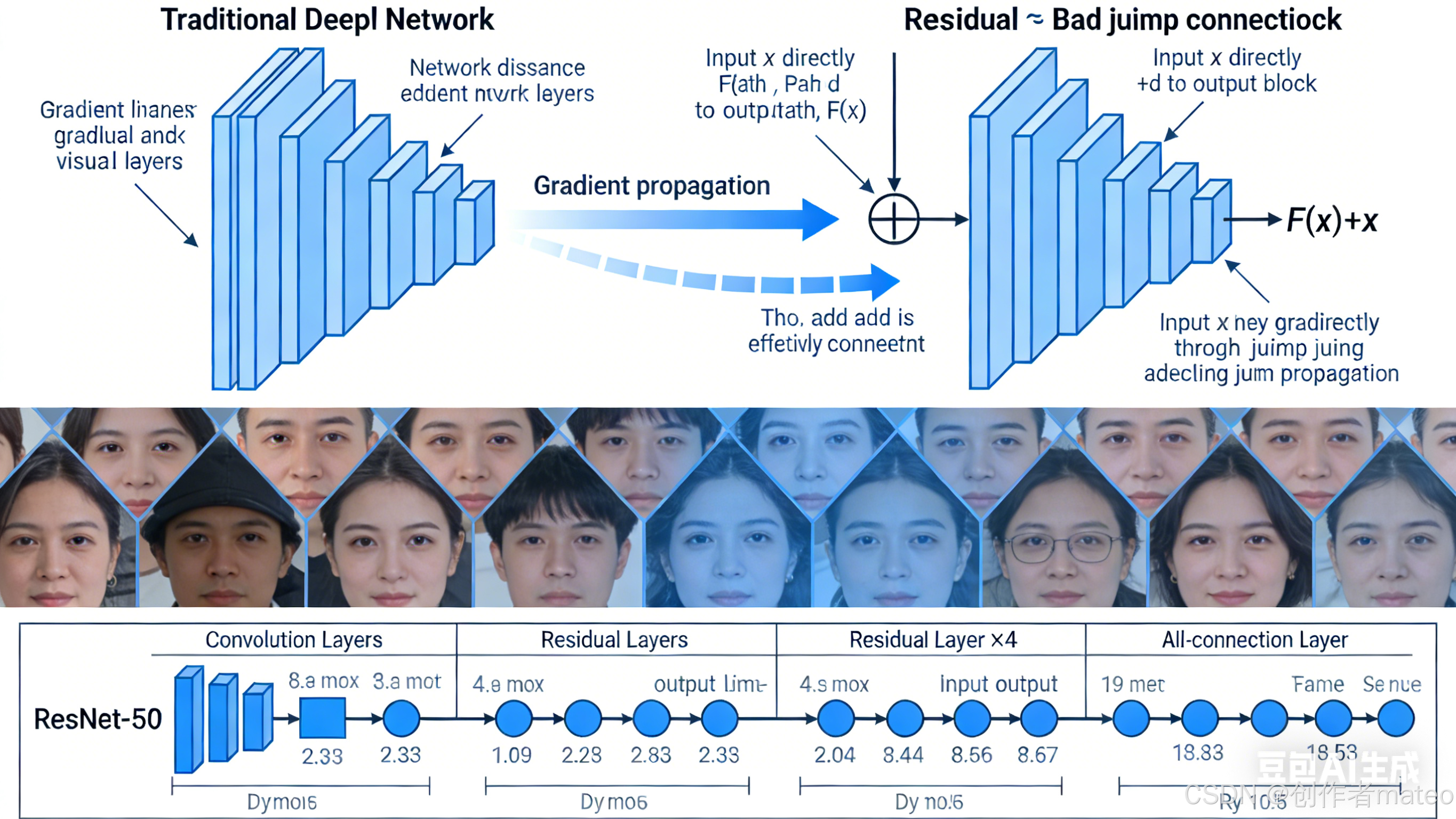
- 残差连接(Residual Connection):通过跳跃连接将输入直接加到输出,梯度可直接通过短路路径传播,避免深层网络的梯度消失。
📌 配图5:残差网络(ResNet)结构示意图
五、写在最后
深度学习并非"黑魔法",其核心逻辑是通过神经网络定义函数集合,用损失函数评估函数质量,再通过梯度下降找到最优函数。随着算力的提升和数据的积累,深度学习仍在快速演进,未来将在更多领域创造价值。