SLAM文献之-A Quick Guide for the Iterated Extended Kalman Filter on Manifolds

摘要

扩展卡尔曼滤波（Extended Kalman Filter，EKF）是一种常用于离散非线性系统的状态估计方法。它随着时间推进递归地执行预测（传播）步骤 ，并在一组测量到达时执行更新步骤 。在更新步骤中，EKF 仅对测量函数进行一次线性化 。相比之下，迭代扩展卡尔曼滤波（Iterated EKF，IEKF）通过在更新步骤中迭代地求解一个最小二乘问题来不断细化状态估计。

IEKF 已被推广到定义在流形上的状态变量，只要该流形定义了可微的 ⊞ 与 ⊟ 运算符，其中也包括 李群（Lie groups） 。然而，现有文献中的相关描述往往冗长、晦涩，甚至存在错误。本文旨在为流形上的 IEKF 提供一个简明的参考说明 ，并仅使用入门级的矩阵微积分进行推导。除给出核心公式外，我们还特别强调了推导过程中所涉及的关键步骤。

I. 问题描述与基本假设

本文要解决的问题是：在已知系统动力学方程 f ( ⋅ ) f(\cdot) f(⋅) 和外部观测 z z z 的情况下，估计系统状态向量 x x x 及其协方差 P P P。

我们假设状态向量 x x x 属于一个可微流形 ，并且该流形上定义了 boxplus（⊞） 和 boxminus（⊟） 运算，其定义为：
x ⊞ δ = y , (1) x \ ⊞ \ \delta = y, \tag{1} x ⊞ δ=y,(1)
y ⊟ x = δ . (2) y \ ⊟ \ x = \delta. \tag{2} y ⊟ x=δ.(2)

其中， y y y 是另一个与 x x x 足够接近的流形元素， δ \delta δ 是描述两者之间"距离"的向量。

在欧氏空间中，⊞ 运算即为通常的加法（ + + +），⊟ 运算即为通常的减法（ − - −）。对于 S O ( 3 ) SO(3) SO(3) 上的元素，⊞ 和 ⊟ 的一种示例性定义可参见式 (20) 和式 (25)。

在状态估计问题中，我们通常用 x ^ \hat{x} x^ 表示对真实状态 x x x 的估计，并通过如下关系将二者联系起来：
x ^ ⊞ δ = x , (3) \hat{x} \ ⊞ \ \delta = x, \tag{3} x^ ⊞ δ=x,(3)
x ⊟ x ^ = δ . (4) x \ ⊟ \ \hat{x} = \delta. \tag{4} x ⊟ x^=δ.(4)

另一种定义方式是 x ⊞ δ = x ^ x \ ⊞ \ \delta = \hat{x} x ⊞ δ=x^，例如在文献 [1] 中采用了这种定义。然而，这种定义会导致卡尔曼更新步骤的形式不够直观，因此在实践中较少使用。

对于扩展卡尔曼滤波（Extended Kalman Filter，EKF），我们使用在时间步 t 1 , ... , t k t_1, \ldots, t_k t1,...,tk 上离散化的系统动力学方程。时间步通常根据测量向量 z z z 的时间戳来选取，例如 z k = z ( t k ) z_k = z(t_k) zk=z(tk) 表示在时间 t k t_k tk 获取的测量。

下面考虑 EKF 的一个时间步，从 t k − 1 t_{k-1} tk−1 到 t k t_k tk，该过程包括两部分：

1）利用离散动力学方程进行预测（传播） ，

2）利用测量 z k z_k zk 进行更新。

从 t k − 1 t_{k-1} tk−1 到 t k t_k tk 的离散动力学方程为：
x k = f ( x k − 1 , u k − 1 , w k − 1 ) , (5) x_k = f(x_{k-1}, u_{k-1}, w_{k-1}), \tag{5} xk=f(xk−1,uk−1,wk−1),(5)

其中， w k − 1 w_{k-1} wk−1 是在 t k − 1 t_{k-1} tk−1 时刻的离散过程噪声，服从高斯分布：
w k − 1 ∼ N ( 0 , Q k − 1 ) . w_{k-1} \sim \mathcal{N}(0, Q_{k-1}). wk−1∼N(0,Qk−1).

在 t k t_k tk 时刻的观测方程为：
z k = h ( x k ) + n k , (6) z_k = h(x_k) + n_k, \tag{6} zk=h(xk)+nk,(6)

其中， n k n_k nk 是在 t k t_k tk 时刻的离散观测噪声，服从高斯分布：
n k ∼ N ( 0 , R k ) . n_k \sim \mathcal{N}(0, R_k). nk∼N(0,Rk).

为简化讨论，我们假设观测噪声是加性噪声 ，且观测 z k z_k zk 位于一个向量空间中。事实上，许多实际的状态估计问题都满足这一假设。

II. 迭代扩展卡尔曼滤波（IEKF）

现在描述迭代扩展卡尔曼滤波（Iterated EKF, IEKF）的状态估计过程。记 t k − 1 t_{k-1} tk−1 时刻的后验状态估计为 x k − 1 + x^+{k-1} xk−1+，协方差为 P k − 1 + P^+{k-1} Pk−1+。

1. 预测（Propagation）步骤

将状态估计传播到 t k t_k tk：
x k − = f ( x k − 1 + , u k − 1 , 0 ) , (7) x^-k = f(x^+{k-1}, u_{k-1}, 0), \tag{7} xk−=f(xk−1+,uk−1,0),(7)
P k − = F k − 1 P k − 1 + F k − 1 T + G k − 1 Q k − 1 G k − 1 T , (8) P^-k = F{k-1} P^+{k-1} F^T{k-1} + G_{k-1} Q_{k-1} G^T_{k-1}, \tag{8} Pk−=Fk−1Pk−1+Fk−1T+Gk−1Qk−1Gk−1T,(8)

其中传播雅可比矩阵为：
F k − 1 = lim ⁡ ϵ → 0 f ( x k − 1 + ⊞ ϵ , u , w ) ⊟ f ( x k − 1 + , u , w ) ϵ , (9) F_{k-1} = \lim_{\epsilon \to 0} \frac{f(x^+{k-1} \ ⊞ \ \epsilon, u, w) \ ⊟ \ f(x^+{k-1}, u, w)}{\epsilon}, \tag{9} Fk−1=ϵ→0limϵf(xk−1+ ⊞ ϵ,u,w) ⊟ f(xk−1+,u,w),(9)
G k − 1 = ∂ f ( x k − 1 + , u , w ) ∂ w ∣ w = 0 . (10) G_{k-1} = \frac{\partial f(x^+{k-1}, u, w)}{\partial w} \Big|{w=0}. \tag{10} Gk−1=∂w∂f(xk−1+,u,w) w=0.(10)

2. 更新（Update）步骤

对于测量 z k z_k zk，标准 EKF 通过最小化预测状态 x k − x^-k xk− 与创新项 z k − h ( x k ) z_k - h(x_k) zk−h(xk) 的加权平方和来求解后验状态 x + ∗ k x^+*k x+∗k：
min ⁡ x k + ( x k + ⊟ x k − ) T ( P k − ) − 1 ( x k + ⊟ x k − ) + ( z k − h ( x k + ) ) T R k − 1 ( z k − h ( x k + ) ) . (11) \min{x^+_k} (x^+_k \ ⊟ \ x^-_k)^T (P^-_k)^{-1} (x^+_k \ ⊟ \ x^-_k) + \\ (z_k - h(x^+_k))^T R_k^{-1} (z_k - h(x^+_k)). \tag{11} xk+min(xk+ ⊟ xk−)T(Pk−)−1(xk+ ⊟ xk−)+(zk−h(xk+))TRk−1(zk−h(xk+)).(11)

与此不同，IEKF 从 x k , 0 + = x k − x^+{k,0} = x^-k xk,0+=xk− 开始，迭代更新 状态向量。在第 j j j 次迭代中，IEKF 计算对当前状态估计 x k , j + x^+{k,j} xk,j+ 的增量 δ k , j \delta{k,j} δk,j，最小化加权平方和：
min ⁡ δ k , j ∣ ∣ ( x k , j + ⊟ x k − + J k , j δ k , j ) ∣ ∣ ( P k − ) − 1 + ∣ ∣ ( z k − h ( x k , j + ) − H k , j δ k , j ) ∣ ∣ R k − 1 ) . (12) \min_{\delta_{k,j}}|| (x^+{k,j} \ ⊟ \ x^-k + J{k,j} \delta{k,j}) ||{(P^-k)^{-1}}+ \\ || (z_k - h(x^+{k,j}) - H{k,j} \delta_{k,j})|| _{R_k^{-1}} ). \tag{12} δk,jmin∣∣(xk,j+ ⊟ xk−+Jk,jδk,j)∣∣(Pk−)−1+∣∣(zk−h(xk,j+)−Hk,jδk,j)∣∣Rk−1).(12)

其中雅可比矩阵定义为：
H k , j = lim ⁡ ϵ → 0 h ( x k , j + ⊞ ϵ ) − h ( x k , j + ) ϵ , (13) H_{k,j} = \lim_{\epsilon \to 0} \frac{h(x^+{k,j} \ ⊞ \ \epsilon) - h(x^+{k,j})}{\epsilon}, \tag{13} Hk,j=ϵ→0limϵh(xk,j+ ⊞ ϵ)−h(xk,j+),(13)
J k , j = lim ⁡ ϵ → 0 ( x k , j + ⊞ ϵ ⊟ x k − ) − ( x k , j + ⊟ x k − ) ϵ . (14) J_{k,j} = \lim_{\epsilon \to 0} \frac{(x^+_{k,j} \ ⊞ \ \epsilon \ ⊟ \ x^-k) - (x^+{k,j} \ ⊟ \ x^-_k)}{\epsilon}. \tag{14} Jk,j=ϵ→0limϵ(xk,j+ ⊞ ϵ ⊟ xk−)−(xk,j+ ⊟ xk−).(14)

如果 x x x 位于向量空间中，则 J k , j J_{k,j} Jk,j 为单位方阵；否则，它可用单位方阵进行良好近似。

3. 求解迭代增量

将 (12) 对 δ k , j \delta_{k,j} δk,j 求导并置零，可得到迭代更新的增量：
S k , j = H k , j L k , j P k − L k , j T H k , j T + R k , (15) S_{k,j} = H_{k,j} L_{k,j} P^-k L{k,j}^T H_{k,j}^T + R_k, \tag{15} Sk,j=Hk,jLk,jPk−Lk,jTHk,jT+Rk,(15)
K k , j = L k , j P k − L k , j T H k , j T S k , j − 1 , (16) K_{k,j} = L_{k,j} P^-k L{k,j}^T H_{k,j}^T S_{k,j}^{-1}, \tag{16} Kk,j=Lk,jPk−Lk,jTHk,jTSk,j−1,(16)
δ k , j = K k , j [ H k , j L k , j T ( x k , j + ⊟ x k − ) + z k − h ( x k , j + ) ] − L k , j T ( x k , j + ⊟ x k − ) , (17) \delta_{k,j} = K_{k,j} \big[ H_{k,j} L_{k,j}^T (x^+{k,j} \ ⊟ \ x^-k) +\\ z_k - h(x^+{k,j}) \big] - L{k,j}^T (x^+{k,j} \ ⊟ \ x^-k), \tag{17} δk,j=Kk,j[Hk,jLk,jT(xk,j+ ⊟ xk−)+zk−h(xk,j+)]−Lk,jT(xk,j+ ⊟ xk−),(17)
x k , j + 1 + = x k , j + ⊞ δ k , j , (18) x^+{k,j+1} = x^+{k,j} \ ⊞ \ \delta_{k,j}, \tag{18} xk,j+1+=xk,j+ ⊞ δk,j,(18)

其中
L k , j = J k , j − 1 . L_{k,j} = J_{k,j}^{-1}. Lk,j=Jk,j−1.

4. 协方差更新

迭代完成后，在最后一次迭代结束时更新协方差：
P k + = ( I − K k , n H k , n ) L k , n P k − L k , n T . (19) P^+k = (I - K{k,n} H_{k,n}) L_{k,n} P^-k L{k,n}^T. \tag{19} Pk+=(I−Kk,nHk,n)Lk,nPk−Lk,nT.(19)

5. 总结

IEKF 的算法流程如 算法 1 所示，通过迭代修正状态估计，相比标准 EKF 可以获得更精确的非线性测量更新。

III. SO3 流形示例

作为示例，当 x x x 是 S O ( 3 ) SO(3) SO(3) 元素时，我们计算 F k − 1 F_{k-1} Fk−1 和 J k , j J_{k,j} Jk,j。设 {B} 坐标系相对于 {W} 坐标系的姿态为 R B W R^W_B RBW，其估计为 R W B b R^b_{W_B} RWBb。

如果我们定义 ⊞ 和 ⊟ 如下（FAST-LIO [2] 中使用方式）：
R W B b ⊞ δ θ W B = R W B b E x p ( δ θ W B ) = R W B , (20) R^b_{W_B} \ ⊞ \ \delta \theta_{WB} = R^b_{W_B} \ \mathrm{Exp}(\delta \theta_{WB}) = R_{W_B}, \tag{20} RWBb ⊞ δθWB=RWBb Exp(δθWB)=RWB,(20)
R W B ⊟ R W B b = L o g ( R W B b T R W B ) = δ θ W B , (21) R_{W_B} \ ⊟ \ R^b_{W_B} = \mathrm{Log}(R^{bT}{W B} R{W_B}) = \delta \theta_{WB}, \tag{21} RWB ⊟ RWBb=Log(RWBbTRWB)=δθWB,(21)

则有：

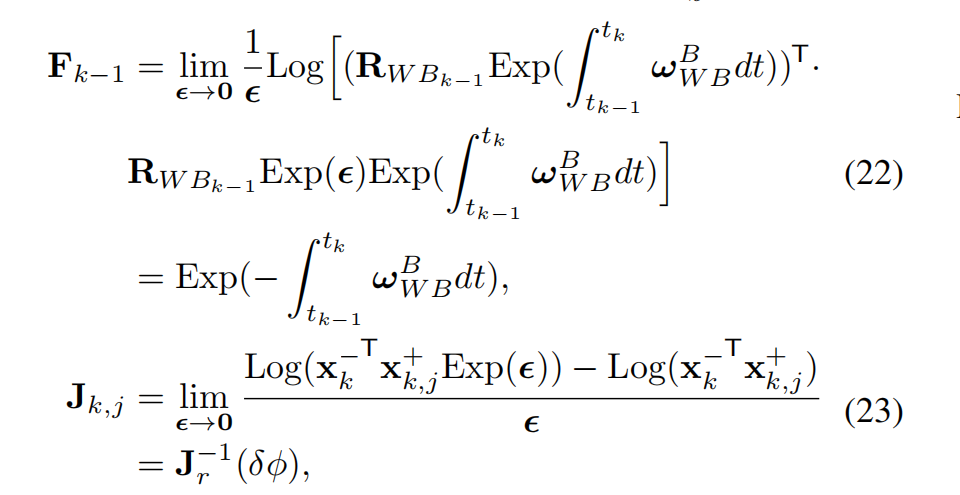
δ ϕ j = x k , j + ⊟ x k − , (24) \delta \phi_j = x^+_{k,j} \ ⊟ \ x^-_k, \tag{24} δϕj=xk,j+ ⊟ xk−,(24)

其中利用角速度关系：

并且 x x x 为旋转矩阵 R W B R_{W_B} RWB。上述结果与 FAST-LIO 方程一致。

如果我们定义 ⊞ 和 ⊟ 如下（如 [3] 所示）：
R W B b ⊞ δ θ W B = E x p ( δ θ W B ) R W B b = R W B , (25) R^b_{W_B} \ ⊞ \ \delta \theta_{WB} = \mathrm{Exp}(\delta \theta_{WB}) R^b_{W_B} = R_{W_B}, \tag{25} RWBb ⊞ δθWB=Exp(δθWB)RWBb=RWB,(25)
R W B ⊟ R W B b = L o g ( R W B R W B b T ) , (26) R_{W_B} \ ⊟ \ R^b_{W_B} = \mathrm{Log}(R_{W_B} R^{bT}_{W B}), \tag{26} RWB ⊟ RWBb=Log(RWBRWBbT),(26)

则有：
F k − 1 = I 3 , (27) F_{k-1} = I_3, \tag{27} Fk−1=I3,(27)
J k , j = lim ⁡ ϵ → 0 L o g ( E x p ( ϵ ) x k , j + ( x k − ) T ) − L o g ( x k , j + ( x k − ) T ) ϵ = J l − 1 ( δ ϕ ) , (28) J_{k,j} = \lim_{\epsilon \to 0} \frac{\mathrm{Log}(\mathrm{Exp}(\epsilon) x^+_{k,j} (x^-k)^T) - \mathrm{Log}(x^+{k,j} (x^-k)^T)}{\epsilon} \\= J_l^{-1}(\delta \phi), \tag{28} Jk,j=ϵ→0limϵLog(Exp(ϵ)xk,j+(xk−)T)−Log(xk,j+(xk−)T)=Jl−1(δϕ),(28)
δ ϕ j = x k , j + ⊟ x k − . (29) \delta \phi_j = x^+{k,j} \ ⊟ \ x^-_k. \tag{29} δϕj=xk,j+ ⊟ xk−.(29)

IV. 相关工作

IEKF 在向量空间中的方法可见于 [4]。
后续扩展到可微流形上的状态向量，如 [5]。
但是，boxplus 运算的雅可比矩阵 L L L 定义 [5, (49)] 模糊，并且在 [5, (50-52)] 中存在转置错误。

事实上， L L L 将流形上的乘法增量与切空间中的加法增量联系起来（参见 (32)）：
L = lim ⁡ ϵ → 0 E x p ( ϕ + ϵ ) ⊟ E x p ( ϕ ) ϵ , (30) L = \lim_{\epsilon \to 0} \frac{\mathrm{Exp}(\phi + \epsilon) \ ⊟ \ \mathrm{Exp}(\phi)}{\epsilon}, \tag{30} L=ϵ→0limϵExp(ϕ+ϵ) ⊟ Exp(ϕ),(30)

其中 E x p \mathrm{Exp} Exp 是可微流形的指数映射 [6]。

对向量， E x p ( x ) = x \mathrm{Exp}(x) = x Exp(x)=x。
对 S O ( 3 ) SO(3) SO(3) 元素， E x p ( ϕ ) = I 3 + ∑ k = 1 ∞ 1 k ! ⌊ ϕ ⌋ × k \mathrm{Exp}(\phi) = I_3 + \sum_{k=1}^\infty \frac{1}{k!} \lfloor \phi \rfloor_\times^k Exp(ϕ)=I3+∑k=1∞k!1⌊ϕ⌋×k。

FAST-LIO [7] 也对流形上的 IEKF 进行了公式化，但内容冗长且符号较多。缺乏一个快速入门参考，是本文动机之一。

另外，X. Gao 的《SLAM 技术在自动驾驶与机器人》一书第 8.3 章也给出了激光惯性里程计的简化 IEKF。

附录：有用的公式

对向量的常用雅可比：
∂ ( a + B x ) T P − 1 ( a + B x ) ∂ x = 2 ( a + B x ) T P − 1 B , (31) \frac{\partial (a + Bx)^T P^{-1} (a + Bx)}{\partial x} = 2 (a + Bx)^T P^{-1} B, \tag{31} ∂x∂(a+Bx)TP−1(a+Bx)=2(a+Bx)TP−1B,(31)
对 S O ( 3 ) SO(3) SO(3) 元素的近似展开：
E x p ( ϕ + δ ϕ ) ≈ E x p ( ϕ ) E x p ( J r ( ϕ ) δ ϕ ) , (32) \mathrm{Exp}(\phi + \delta \phi) \approx \mathrm{Exp}(\phi) \mathrm{Exp}(J_r(\phi) \delta \phi), \tag{32} Exp(ϕ+δϕ)≈Exp(ϕ)Exp(Jr(ϕ)δϕ),(32)
J r ( ϕ ) = I 3 − 1 − cos ⁡ θ θ 2 ⌊ ϕ ⌋ × + θ − sin ⁡ θ θ 3 ⌊ ϕ ⌋ × 2 , (33) J_r(\phi) = I_3 - \frac{1 - \cos \theta}{\theta^2} \lfloor \phi \rfloor_\times + \frac{\theta - \sin \theta}{\theta^3} \lfloor \phi \rfloor_\times^2, \tag{33} Jr(ϕ)=I3−θ21−cosθ⌊ϕ⌋×+θ3θ−sinθ⌊ϕ⌋×2,(33)
E x p ( ϕ + δ ϕ ) ≈ E x p ( J l ( ϕ ) δ ϕ ) E x p ( ϕ ) , (34) \mathrm{Exp}(\phi + \delta \phi) \approx \mathrm{Exp}(J_l(\phi) \delta \phi) \mathrm{Exp}(\phi), \tag{34} Exp(ϕ+δϕ)≈Exp(Jl(ϕ)δϕ)Exp(ϕ),(34)
J r − 1 ( ϕ ) = I 3 + 1 2 ⌊ ϕ ⌋ × + ( θ 2 − 1 − cos ⁡ θ 2 θ sin ⁡ θ ) ⌊ ϕ ⌋ × 2 , (35) J_r^{-1}(\phi) = I_3 + \frac{1}{2} \lfloor \phi \rfloor_\times + \Big(\frac{\theta}{2} - \frac{1 - \cos \theta}{2 \theta \sin \theta} \Big) \lfloor \phi \rfloor_\times^2, \tag{35} Jr−1(ϕ)=I3+21⌊ϕ⌋×+(2θ−2θsinθ1−cosθ)⌊ϕ⌋×2,(35)
J r T ( ϕ ) = J l ( ϕ ) = J r ( − ϕ ) , (36) J_r^T(\phi) = J_l(\phi) = J_r(-\phi), \tag{36} JrT(ϕ)=Jl(ϕ)=Jr(−ϕ),(36)
J r − T ( ϕ ) = J l − 1 ( ϕ ) = J r − 1 ( − ϕ ) . (37) J_r^{-T}(\phi) = J_l^{-1}(\phi) = J_r^{-1}(-\phi). \tag{37} Jr−T(ϕ)=Jl−1(ϕ)=Jr−1(−ϕ).(37)