数据结构第五章：树与二叉树

一、树的基本概念（基础必考）

✅ 树的定义

• 树（Tree） 是一个非线性结构，由 n（n ≥ 0）个节点组成。
• 满足：
  • 有且仅有一个根节点
  • 其余节点分为 m（m ≥ 0）个互不相交的子集，每个子集本身也是一棵树（称为子树）

🔑 基本术语

术语	含义
父节点/子节点	直接相连的两个节点中，上为父，下为子
兄弟节点	同一个父节点下的节点
度	一个节点的子树个数
叶子节点	度为 0 的节点
深度	根到该节点的路径长度（根深度为 0 或 1，视题目而定）
高度	从该节点到最远叶子的距离（叶子高度为 0）

💡 考点：判断树的度、深度、高度；区分"深度"与"高度"

---

二、二叉树（重中之重！）

✅ 定义与特征

二叉树 是每个节点最多有两个子树的有序树，子树分为左子树 和右子树。

✅ 主要特征：

1. 左右子树顺序不可交换
2. 第 i 层最多有 2i−12i−1 个节点
3. 深度为 k 的二叉树最多有 2k−12k−1 个节点
4. 任意二叉树中，叶子节点数 = 度为 2 的节点数 + 1

💡 考点：计算最大节点数、叶子节点数、度为 2 的节点数

---

✅ 存储结构

1. 顺序存储结构

• 用数组存储完全二叉树
• 规律：
  • 若根在 arr[0]，则：
    • 左孩子：2*i + 1
    • 右孩子：2*i + 2
    • 父亲：(i-1)/2

✅ 优点：节省空间，便于访问

❌ 缺点：只适用于完全二叉树，插入删除效率低

2. 链式存储结构（常用）

typedef struct BiTNode {
	ElemType data; // 数据域
	struct BiTNode *lchild, *rchild; // 左、右孩子指针
} BiTNode, *BiTree;

✅ 二叉树的遍历（核心考点）

类型	顺序	特点
前序遍历	根 → 左 → 右	用于复制树、表达式求值
中序遍历	左 → 根 → 右	二叉搜索树中可得有序序列
后序遍历	左 → 右 → 根	用于删除树、释放内存

💡 考点：手写遍历序列、已知两种遍历还原树、判断是否为二叉搜索树

---

✅ 线索二叉树（优化遍历）

✅ 问题：

• 二叉树遍历需要栈或递归，无法直接访问前驱/后继

✅ 解决方案：线索化

• 利用空指针域存放前驱或后继信息
• 分为：
  • 前序线索树
  • 中序线索树（最常用）
  • 后序线索树

✅ 中序线索树示例：

• 若左孩子为空，则指向中序前驱
• 若右孩子为空，则指向中序后继

💡 考点：理解线索化的思想，能画出中序线索树

---

三、树与森林

✅ 树的存储结构

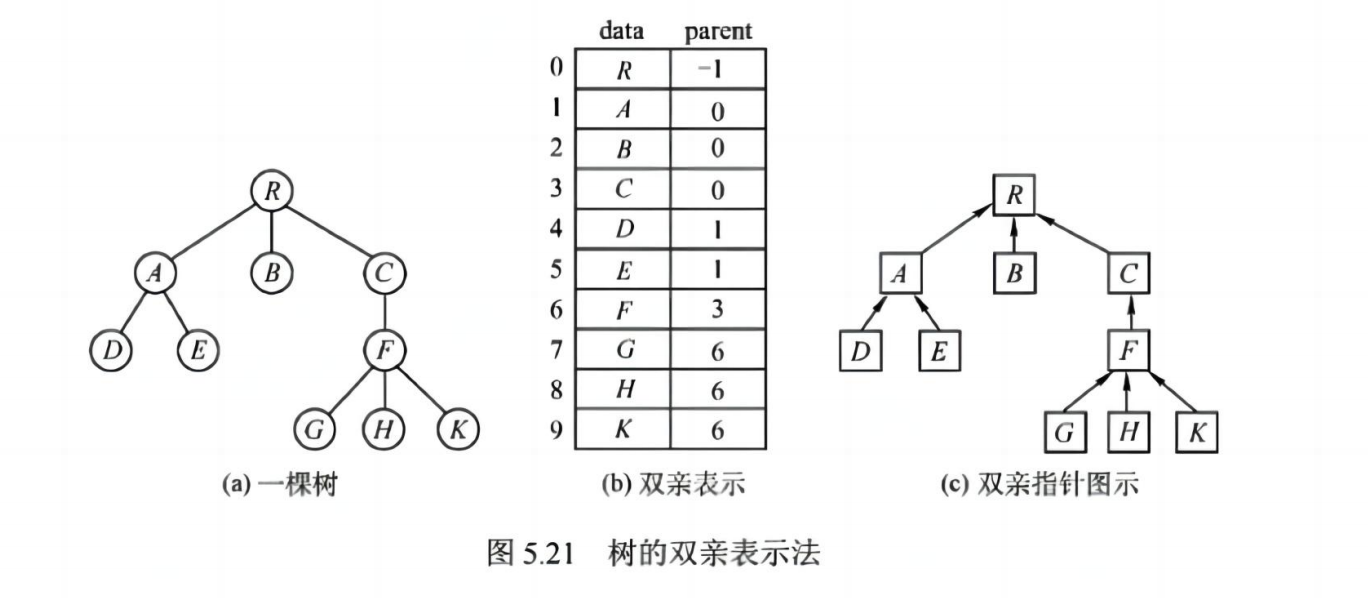
1. 双亲表示法

• 每个节点记录其父节点编号
• 适合查找父节点

#define MAX_TREE_SIZE 100 // 书中最多结点数

typedef struct { // 树的结点定义
	ElemType data; // 数据元素
	int parent; // 双亲位置域
} PTNode;

typedef struct { // 树的类型定义
	PTNode nodes[MAX_TREE_SIZE]; // 双亲表示
	int n; // 结点数
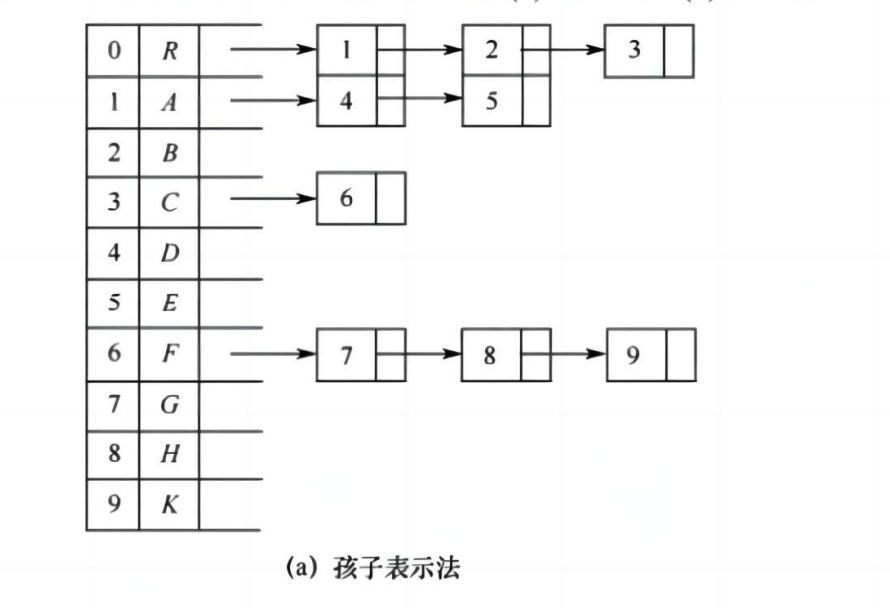
} PTree;

2. 孩子表示法

• 每个节点存储其所有孩子
• 适合查找子树

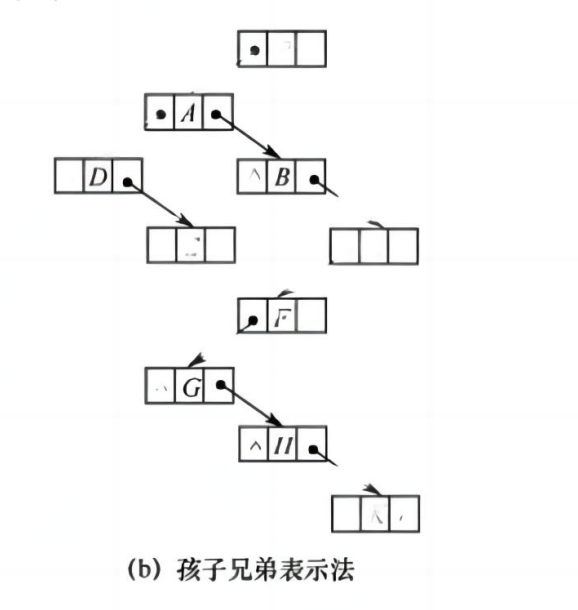
3. 孩子兄弟表示法（重要！）

• 每个节点有两个指针：
  • firstchild：指向第一个孩子
  • nextsibling：指向下一个兄弟
• 优点：可将树转化为二叉树

typedef struct CSNode {
	ElemType data; // 数据域
	struct CSNode *lchild, *nextsibling; // 第一个孩子和兄弟结点
} CSNode, *CSTree;

---

✅ 森林与二叉树的转换

✅ 核心思想：

• 将森林中的每棵树按"孩子兄弟表示法"转换为二叉树
• 多棵树之间通过兄弟关系连接

✅ 转换规则：

1. 第一棵树：根为新二叉树的根
2. 后续树：作为前一棵树的右兄弟
3. 每个节点：左孩子是第一个孩子，右孩子是下一个兄弟

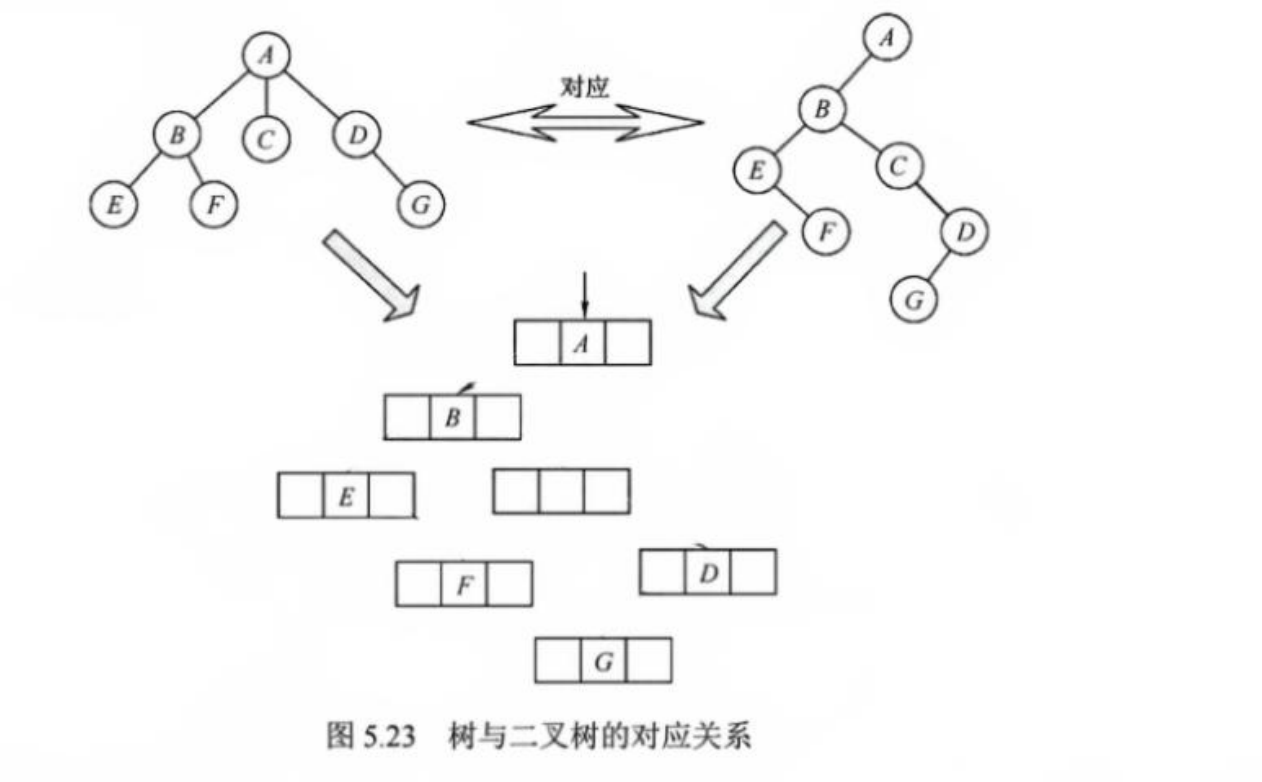
💡 考点：会画树→二叉树、森林→二叉树的转换图

---

✅ 树和森林的遍历

表格

遍历方式	树	森林
先根遍历	根 → 子树先根	树先根 → 森林先根
后根遍历	子树后根 → 根	森林后根 → 树后根

💡 注意：树的先根遍历 ≈ 二叉树的前序遍历

树的后根遍历 ≈ 二叉树的后序遍历

---

四、树与二叉树的应用

✅ 哈夫曼（Huffman）树与编码

✅ 哈夫曼树定义：

• 一棵带权路径长度最小的二叉树
• 所有叶子节点有权重（如字符频率）

✅ 构造方法（贪心）：

1. 将所有叶子节点放入优先队列（小顶堆）
2. 取出两个最小权值的节点，合并为一个新节点（权值为和）
3. 将新节点放回队列
4. 重复直到只剩一个节点（根）

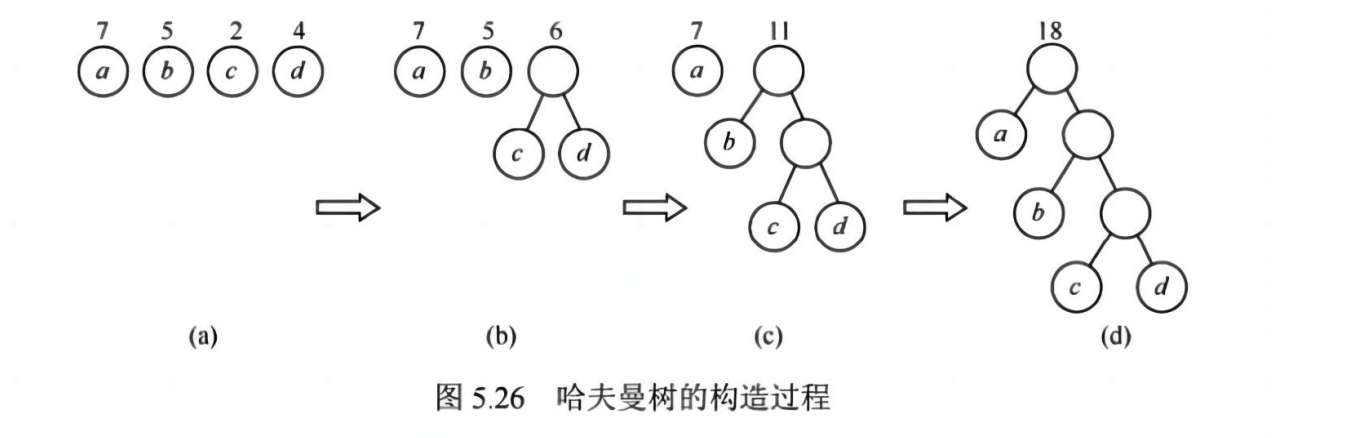
💡 考点：构造哈夫曼树、计算带权路径长度（WPL）、写出哈夫曼编码

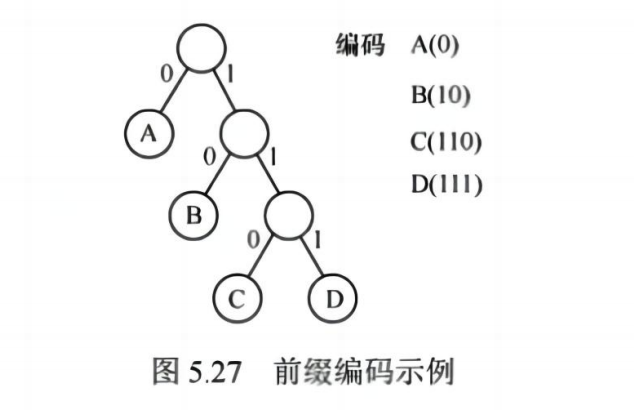
✅ 哈夫曼编码

• 每个字符对应从根到叶子的一条路径
• 左边标 0，右边标 1
• 得到唯一前缀码（无歧义）

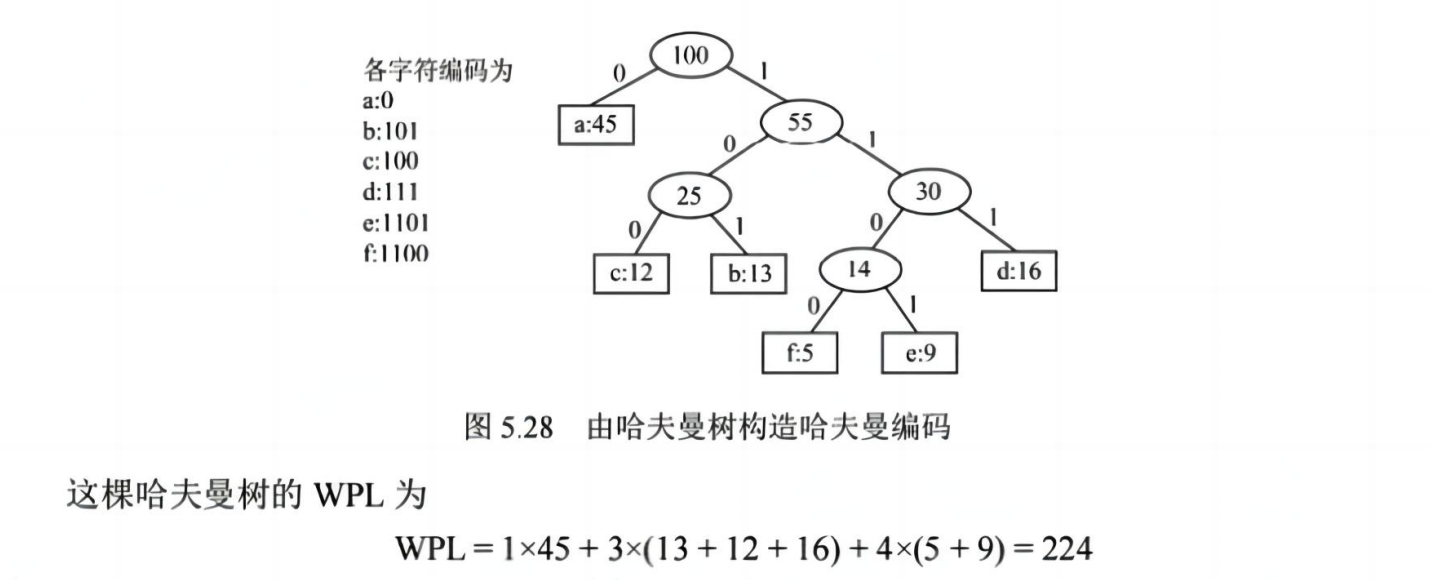
✅ 优点：压缩率高，广泛用于文件压缩（ZIP、JPEG）

---

✅ 并查集（Union-Find）

✅ 定义：

• 一种用于管理集合合并与查询的数据结构
• 支持两种操作：
  • find(x)：查找 x 所在集合的代表元（根）
  • union(x, y)：合并 x 和 y 所在集合

#define SIZE 100
int UFSets[SIZE]; // 集合元素数组（双亲指针数组）

// 并查集的初始化操作
void Initial(int S[]) { // S即为并查集
	for(int i = 0; i < SIZE; i++) { // 每个自成单元素集合
		S[i] = -1;
	}
}

// Find操作
int Find(int S[], int x) {
	int root = x;
	while(S[root] >= 0) { // 循环查找x的根
		root = S[root];
	}
	while(x != root) { // 压缩路径
		int t = S[x]; // t指向x的父结点
		S[x] = root; // x直接挂载到根结点下面
		x = t;
	}
	return root; // 返回根结点编号
}

// Union操作
void Union(int S[], int Root1, int Root2) {
	if(Root1 == Root2) return; // 要求Root1和Root2是不同的集合
	if(S[Root2] > S[Root1]) { // Root2结点数更少
		S[Root1] += S[Root2]; // 累加到集合树的结点总数
		S[Root2] = Root1; // 小树合并大树
	} else { // Root1结点数更少
		S[Root2] += S[Root1]; // 累加结点总数
		S[Root1] = Root2; // 小树合并大树
	}
}

✅ 实现方式：

• 用数组存储父节点
• 使用路径压缩 和按秩合并优化效率

✅ 时间复杂度：

• 近似 O(α(n))，其中 α(n) 是阿克曼函数的反函数（极慢增长）

💡 应用场景：

• 图的连通性检测
• 最小生成树（Kruskal 算法）
• 等价类问题（如朋友圈）

✅ 考点：理解并查集原理，能实现 find 和 union 函数

---

五、高频考点总结

题型	考点
选择题	- 二叉树性质（叶子数、度为2的节点数） - 遍历顺序 - 哈夫曼树 WPL 计算 - 并查集时间复杂度
填空题	- 写出前/中/后序遍历序列 - 哈夫曼编码表
简答题	- 说明线索化的作用 - 描述森林转二叉树的过程 - 解释并查集如何维护集合
算法题	- 构造哈夫曼树 - 实现并查集的 find 和 union

---

六、一句话口诀（背下来！）

"二叉树三种遍历，线索化方便找前后；
树转二叉靠兄弟，哈夫曼编码省空间；
并查集合并快，路径压缩效率高！"

---