【C++】：搜索二叉树的模拟实现

小六子成长记2026-01-16 19:58

目录

1.搜索二叉树的性质

2.模拟实现

2.1构建节点

2.2.树的结构

[2.3 插入数据](#2.3 插入数据)

[2.4 删除数据](#2.4 删除数据)

[2.5 查找数据](#2.5 查找数据)

[2.6 中序遍历](#2.6 中序遍历)

[2.6 析构函数](#2.6 析构函数)

[2.7 拷贝构造](#2.7 拷贝构造)

[2. 8 operator= 重载 （现代写法）](#2. 8 operator= 重载 （现代写法）)

3.总结

4.使用方式

[4. 整体程序](#4. 整体程序)

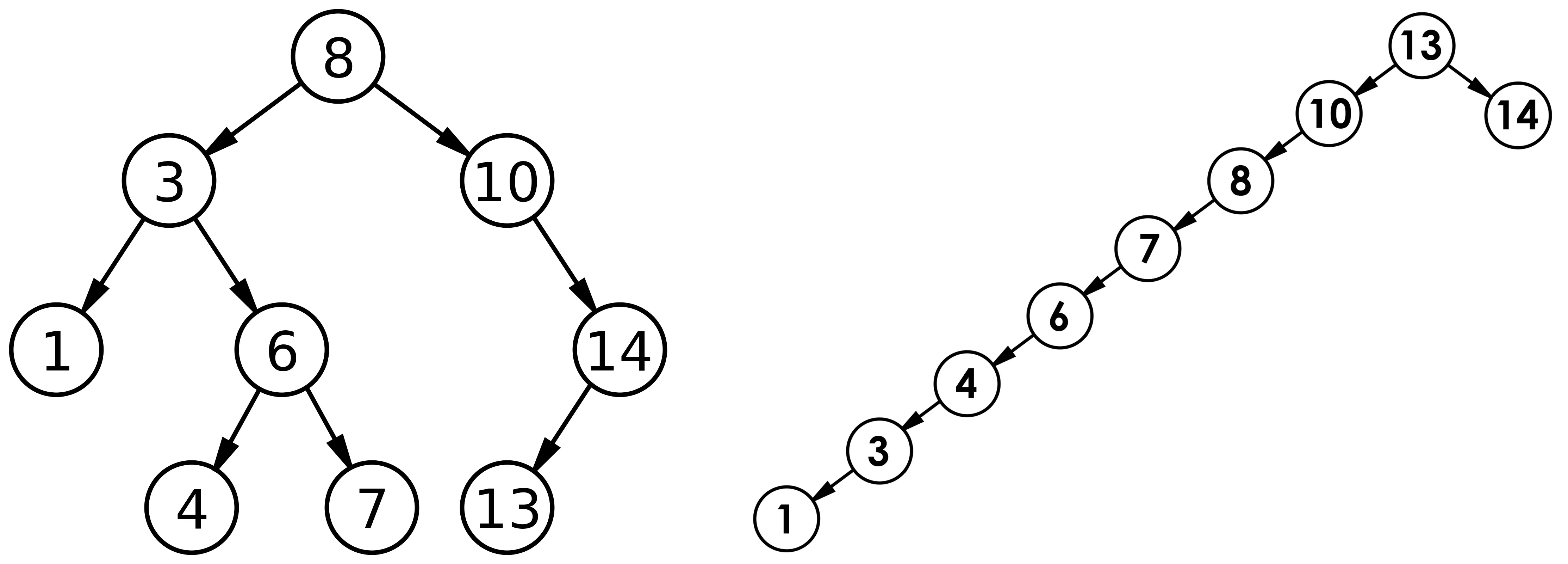
1.搜索二叉树的性质

搜索二叉树是在二叉树的上加入了一些特性，

  • 左子树的节点小于根节点的值；
  • 右子树的节点大于根节点的值。
  • 左右子树均为搜索二叉树

2.模拟实现

2.1构建节点

首先构建节点，包含指向左右孩子的指针 ，以及存储的值。

cpp 复制代码 
template <class K>
class BSTreeNode
{
public:
	BSTreeNode<K>* _right;
	BSTreeNode<K>* _left;
	K _key;
	BSTreeNode(const K& key)
		:_right(nullptr)
		, _left(nullptr)
		, _key(key)
	{}
};

由于是指针和K（后面的给的值有内置类型）需要显示构造 ，或者给缺省值，指针指向随机值，指向混乱。

2.2.树的结构

二叉树的采用链式结构 。根节点是整棵树的唯一入口，所有节点都通过根节点的左右指针串联，无需额外成员变量就能访问 / 操作整棵树。

cpp 复制代码 
template <class K>
class BSTree
{
	
public:
    BSTree（）
    {
       _root = nullptr;
    }
private：
	Node* _root;
};

2.3 插入数据

  1. 树为空，直接插入
  2. 树不为空，根据插入值的大小，判断遍历的方向
  3. 等访问到空节点时候停止，插入新的节点。

1.遍历实现

cpp 复制代码 
bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
	
			return true;
		}
		//寻找位置

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if  (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		Node* newnode = new Node(key);

		if (parent->_key > key)
		{
			parent->_left = newnode;
			return true;
		}
		
		else
		{
			parent->_right = newnode;
			return true;
		}
		return false;//插入失败的
	}

2.递归实现

cpp 复制代码 
bool InsertR (const K& key)
	{
		return _InsertR(_root, key);
	}
bool _InsertR(Node*& root, const K& key)
// 这个引用是重中之重，因为引用相当于别名，所以树才可以连接上
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}
		//寻找位置
		if (root->_key > key)
		{
			return _InsertR(root->_left, key);

		}
		else if (root->_key < key)
		{
			return _InsertR(root->_right, key);
		}
		else
		{
			return false;
		}
	}

形参列表中的引用，root为插入位置，如果删去引用，变为拷贝，即形参的修改不会影响实参，创建的节点无法挂在树上。

2.4 删除数据

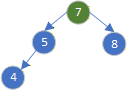
先找到目标节点，再分三种情况删除（左空 / 右空 / 左右都有），

1.没有孩子的节点直接删除

2.有一个孩子的节点，左孩子和右孩子，直接交给父亲节点

3.有两个孩子的节点 ，找到左子树最大 （左子树最右边节点）的或者右子树最小（最左边节点）的节点，将最大或者最小节点和被删除的节点的值交换 ，然后删除最大或者最小节点。也就是将两个孩子转换成了一个孩子或者没有孩子。

最后删除节点，释放内存

注意： 第三种情况最后删除的时候可以遵守有一个孩子和没有孩子的情况，leftMax可能是父亲的左节点，也有可能是父亲的左节点（这种肯定有）

特例需要注意。

遍历方式

cpp 复制代码 
bool Erase(const K& key)
 {
		if (_root == nullptr)
		{
			return false;
		}
		//总体的目的就是寻找到cur，然后将删除，没有孩子和单个孩子看为一种 都是指向空

		Node* cur = _root;
		Node* parent = cur;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else//找到节点 
			{
				//父母只有一个孩子或者没有孩子的情况
				if (cur->_left == nullptr)//左孩子为空 只有左节点或者没有节点的
				{
					if (cur == _root)//删除的节点是根节点 
						_root = cur->_right;
					else 
					{
						if (parent->_right == cur)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}

					}
				}
				else if (cur->_right == nullptr) // 没有右孩子
				{

					if (cur == _root)//删除的节点是根节点 
						_root = cur->_left;
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_left;
// cur节点在parent的左边就放在左边，右边就连接右边
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

				}
				else//有两个孩子的
				{
					Node* parent = cur;
					Node* leftMax = cur->_left; //找到可以替代的中间节点
					while (leftMax->_right)
					{
						parent = leftMax;
						leftMax = leftMax->_right;
					}
					swap(cur->_key, leftMax->_key);
					if (parent->_left == leftMax)
					{
						parent->_left = leftMax->_left;//这颗子树的左边就是最大值的情况，
					}
					else
					{
						parent->_right = leftMax->_left;
					}
					cur = leftMax;//

				}
				delete cur;
				cur = nullptr;
				return true;
			}
		}
		
		return false;	
	}

递归方式

cpp 复制代码 
    bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}
	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			return false;
		}
		//寻找位置
		if (root->_key > key)
		{
			return _EraseR(root->_left, key);

		}
		else if (root->_key < key)
		{
			return _EraseR(root->_right, key);
		}
		else//找到了
		{
			//三种情况，一种是 左子树有 右子树有，两个子树都有
			Node* del = root;
			if(root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			
			}
			else//存在问题
			{
				Node* leftMax = root->_left;
				while (leftMax->_right)
				{
					leftMax = leftMax->_right;
				}
				swap(leftMax->_key, root->_key);
				return _EraseR(root->_left, key);//在递归在字数中找到这个key然后删除
			}
			delete del;
			return true;
		}
	}

2.5 查找数据

查找数据最为简便，

查找值大于节点值，向右遍历，小于节点值，向左遍历啊。

遍历方式

cpp 复制代码 
bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

递归方式

cpp 复制代码 
bool FindR(const K& key)
	{
		return _FindR(_root, key);
	}

Node* _FindR(Node*root, const K& key)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		if (root->_key > key)
		{
			return _FindR(root->_left, key);
		}
		else if (root->_key < key)
		{
			return _FindR(root->_right, key);
		}
		else//相等返回的值
		{
			return root;
		}
	}

2.6 中序遍历

采用先左，中根，后右顺序遍历二叉树

cpp 复制代码 
//中序遍历
	void InOrder()
	{
		_Inorder(_root);
		cout << endl;
	}

void _Inorder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		//中序遍历；左根右
		_Inorder(root->_left);
		cout << root->_key<< " ";
		_Inorder(root->_right);
	}

2.6 析构函数

自定义类型的析构函数，由于类中使用了new动态内存，必须使用显示析构函数

递归的方式

cpp 复制代码 
~BSTree()
{
	Destory(_root);
}
void Destory(Node*& root)
{
	if (root == nullptr)
	{
		return;
	}
	Destory(root->_left);//限制条件在前，操作在后
	Destory(root->_right);
	delete root;
	root = nullptr;
}

2.7 拷贝构造

cpp 复制代码 
BSTree(const BSTree<K>& t)
{
	_root = Copy(t._root);
}
Node* Copy(Node* root)
{
	if (root == nullptr)
	{
		return nullptr;
	}
	Node* copynode = new  Node(root->_key);
	copynode->_left = Copy(root->_left);
	copynode->_right = Copy(root->_right);
	return copynode;
}

2. 8 operator= 重载 （现代写法）

cpp 复制代码 
BSTree<K>& operator=(BSTree<K> t)//拷贝构造
{
	swap(_root, t._root);//交换
	return *this;//返回拷贝构造值，销毁局部对象
}

3.总结

插入和删除操作都必须先查找 ，查找效率 代表了二叉搜索树 中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二
叉搜索树的深度的函数，即结点越深 ，则 比较次数越多。

最优情况下，二叉搜索树为完全二叉树 ( 或者接近完全二叉树 ) ，其平均比较次数为：O（logN）
最差情况下，二叉搜索树退化为单支树 ( 或者类似单支 ) ，其平均比较次数为： O（N）
为了保证二叉树的搜索效率，创建了平衡搜索二叉树（AVL树和红黑树）

4.使用方式

搜索二叉树的值本身为一种键值，key无法修改，需要一个value，key和value凑成键值对，这
样我们可以通过key寻找value，查找方便快捷，以及计数。pair形式的存储。
使用用例如下，均为KV模型（map），一个是计数，以及是英语字典。
一种为K模型，即K即使规律排序，便于查找。

cpp 复制代码 
namespace XLZ
{
	template <class K, class V >
	class BSTreeNode
	{
	public:
		BSTreeNode<K, V>* _right;
		BSTreeNode<K, V>* _left;
		K _key;
		V _value;
		BSTreeNode(const K& key, const V& value)
			:_right(nullptr)
			, _left(nullptr)
			, _key(key)
			, _value(value)
		{}
	};

	template <class K, class V>
	class BSTree
	{

	public:
		typedef  BSTreeNode<K, V> Node;
		//构造函数
		BSTree()
		{
			_root = nullptr;
		}
		~BSTree()
		{
			Destory(_root);
		}
		BSTree(const BSTree<K, V>& t)
		{
			_root = Copy(t._root);
		}
		BSTree<K, V>& operator=(BSTree<K, V> t)
		{
			swap(_root, t._root);
			return *this;
		}
		//二叉树使用递归是最为方便的，因此这里演示递归的使用方式
		//查询函数
		Node* FindR(const K& key)
		{
			return _FindR(_root, key);
		}
		bool InsertR(const K& key, const V& value)
		{
			return _InsertR(_root, key, value);
		}
		bool EraseR(const K& key)
		{
			return _EraseR(_root, key);
		}

		//中序遍历
		void InOrder()
		{
			_Inorder(_root);
			cout << endl;
		}
	private:
		Node* Copy(Node* root)
		{
			if (root == nullptr)
			{
				return nullptr;
			}
			Node* copynode = new  Node(root->_key);
			copynode->_left = Copy(root->_left);
			copynode->_right = Copy(root->_right);
			return copynode;
		}


		void Destory(Node*& root)
		{
			if (root == nullptr)
			{
				return;
			}
			Destory(root->_left);//限制条件在前，操作在后
			Destory(root->_right);
			delete root;
			root = nullptr;
		}

		Node* _FindR(Node*root, const K& key)
		{
			if (root == nullptr)
			{
				return nullptr;
			}
			if (root->_key > key)
			{
				return _FindR(root->_left, key);
			}
			else if (root->_key < key)
			{
				return _FindR(root->_right, key);
			}
			else//相等返回的值
			{
				return root;
			}
		}
		bool _InsertR(Node*& root, const K& key, const V& value)// 这个引用是重中之重，因为引用相当于别名，所以树才可以连接上
		{
			if (root == nullptr)
			{
				root = new Node(key,value);
				return true;
			}
			//寻找位置
			if (root->_key > key)
			{
				return _InsertR(root->_left, key,value);

			}
			else if (root->_key < key)
			{
				return _InsertR(root->_right, key,value);
			}
			else
			{
				return false;
			}
		}
		bool _EraseR(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				return false;
			}
			//寻找位置
			if (root->_key > key)
			{
				return _EraseR(root->_left, key);

			}
			else if (root->_key < key)
			{
				return _EraseR(root->_right, key);
			}
			else//找到了
			{
				//三种情况，一种是 左子树有 右子树有，两个子树都有
				Node* del = root;
				if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else if (root->_right == nullptr)
				{
					root = root->_left;

				}
				else//存在问题
				{
					Node* leftMax = root->_left;
					while (leftMax->_right)
					{
						leftMax = leftMax->_right;
					}
					swap(leftMax->_key, root->_key);
					return _EraseR(root->_left, key);//在递归在字数中找到这个key然后删除
				}
				delete del;
				return true;
			}
		}

		void _Inorder(Node* root)
		{
			if (root == nullptr)
			{
				return;
			}
			//中序遍历；左根右
			_Inorder(root->_left);
			//printf("%s:%d", root->_key, root->_value);
			cout << root->_key << ":" << root->_value << endl;
			_Inorder(root->_right);
		}
		Node* _root;
	};
	//创建一个词典
	void TestBSTree1()
	{
		BSTree<string, string>dict;
		dict.InsertR("insert", "插入");
		dict.InsertR("erase", "删除");
		dict.InsertR("data", "日期");
		dict.InsertR("hello", "你好");
		dict.InsertR("sorry", "对不起");
		//输入单词
		string str;
		while (cin >> str)
		{
			auto ret = dict.FindR(str);
			if (ret == nullptr)
				cout << "nothig" << endl;
			else
				cout << ret->_value << endl;

		}

	}
	void TestBSTree2()
	{
		// 11:44继续
		// 统计水果出现的次数
		string arr[] = { "西瓜", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
		XLZ::BSTree<string, int> countTree;
		for (auto& str : arr)
		{
			auto ret = countTree.FindR(str);
			if (ret == nullptr)
			{
				countTree.InsertR(str, 1);
			}
			else
			{
				ret->_value++;
			}
		}
		countTree.InOrder();

	}
}

4. 整体程序

cpp 复制代码 
#include <iostream>
#include <string>
using namespace std;
//二叉搜索树的底层实现
template <class K>
class BSTreeNode
{
public:
	BSTreeNode<K>* _right;
	BSTreeNode<K>* _left;
	K _key;
	BSTreeNode(const K& key)
		:_right(nullptr)
		, _left(nullptr)
		, _key(key)
	{}
};

template <class K>
class BSTree
{
	
public:
	typedef  BSTreeNode<K> Node;
	//构造函数
	BSTree()
	{
		_root = nullptr;
	}
	~BSTree()
	{
		Destory(_root);
	}
	BSTree(const BSTree<K>& t) 
	{
		_root = Copy(t._root);	
	}
	BSTree<K>& operator=( BSTree<K> t)
	{
		swap(_root, t._root);
		return *this;
	}


	//插入函数
	bool Insert(const K& key)
	{
		if (_root == nullptr)
		{
			_root = new Node(key);
	
			return true;
		}
		//寻找位置

		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if  (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		Node* newnode = new Node(key);

		if (parent->_key > key)
		{
			parent->_left = newnode;
			return true;
		}
		
		else
		{
			parent->_right = newnode;
			return true;
		}
		return false;//插入失败的，基本没有吧
	}
	bool Erase(const K& key)
	{
		if (_root == nullptr)
		{
			return false;
		}
		//总体的目的就是寻找到cur，然后将删除，没有孩子和单个孩子看为一种 都是指向空

		Node* cur = _root;
		Node* parent = cur;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else//找到节点 
			{
				//父母只有一个孩子或者没有孩子的情况
				if (cur->_left == nullptr)//左孩子为空 只有左节点或者没有节点的
				{
					if (cur == _root)//删除的节点是根节点 
						_root = cur->_right;
					else 
					{
						if (parent->_right == cur)
						{
							parent->_right = cur->_right;
						}
						else
						{
							parent->_left = cur->_right;
						}

					}
				}
				else if (cur->_right == nullptr) // 没有右孩子
				{

					if (cur == _root)//删除的节点是根节点 
						_root = cur->_left;
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_left;// cur节点在parent的左边就放在左边 ，右边就连接右边
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

				}
				else//有两个孩子的
				{
					Node* parent = cur;
					Node* leftMax = cur->_left; //找到可以替代的中间节点
					while (leftMax->_right)
					{
						parent = leftMax;
						leftMax = leftMax->_right;
					}
					swap(cur->_key, leftMax->_key);
					if (parent->_left == leftMax)
					{
						parent->_left = leftMax->_left;//这颗子树的左边就是最大值的情况，
					}
					else
					{
						parent->_right = leftMax->_left;
					}
					cur = leftMax;//

				}
				delete cur;
				cur = nullptr;
				return true;
			}
		}
		
		return false;
		
	}
	bool Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;
			}
		}
		return false;
	}
	//二叉树使用递归是最为方便的，因此这里演示递归的使用方式
	//查询函数
	bool FindR(const K& key)
	{
		return _FindR(_root, key);
	}
	bool InsertR (const K& key)
	{
		return _InsertR(_root, key);
	}
	bool EraseR(const K& key)
	{
		return _EraseR(_root, key);
	}

	//中序遍历
	void InOrder()
	{
		_Inorder(_root);
		cout << endl;
	}
private:
	
	
	BSTree(const BSTree<K>& t)
	{
		_root = Copy(t._root);
	}
	Node* Copy(Node* root)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		Node* copynode = new  Node(root->_key);
		copynode->_left = Copy(root->_left);
		copynode->_right = Copy(root->_right);
		return copynode;
	}


	void Destory(Node*& root)
	{
		if (root == nullptr)
		{
			return;
		}
		Destory(root->_left);//限制条件在前，操作在后
		Destory(root->_right);
		delete root;
		root = nullptr;
	}

	Node* _FindR(Node*root, const K& key)
	{
		if (root == nullptr)
		{
			return nullptr;
		}
		if (root->_key > key)
		{
			return _FindR(root->_left, key);
		}
		else if (root->_key < key)
		{
			return _FindR(root->_right, key);
		}
		else//相等返回的值
		{
			return root;
		}
	}
	bool _InsertR(Node*& root, const K& key)// 这个引用是重中之重，因为引用相当于别名，所以树才可以连接上
	{
		if (root == nullptr)
		{
			root = new Node(key);
			return true;
		}
		//寻找位置
		if (root->_key > key)
		{
			return _InsertR(root->_left, key);

		}
		else if (root->_key < key)
		{
			return _InsertR(root->_right, key);
		}
		else
		{
			return false;
		}
	}

	bool _EraseR(Node*& root, const K& key)
	{
		if (root == nullptr)
		{
			return false;
		}
		//寻找位置
		if (root->_key > key)
		{
			return _EraseR(root->_left, key);

		}
		else if (root->_key < key)
		{
			return _EraseR(root->_right, key);
		}
		else//找到了
		{
			//三种情况，一种是 左子树有 右子树有，两个子树都有
			Node* del = root;
			if(root->_left == nullptr)
			{
				root = root->_right;
			}
			else if (root->_right == nullptr)
			{
				root = root->_left;
			
			}
			else//存在问题
			{
				Node* leftMax = root->_left;
				while (leftMax->_right)
				{
					leftMax = leftMax->_right;
				}
				swap(leftMax->_key, root->_key);
				return _EraseR(root->_left, key);//在递归在字数中找到这个key然后删除
			}
			delete del;
			return true;
		}
	}

	void _Inorder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		//中序遍历；左根右
		_Inorder(root->_left);
		cout << root->_key<< " ";
		_Inorder(root->_right);
	}
	Node* _root;
};
相关推荐
汉克老师2 小时前
GESP2025年9月认证C++二级真题与解析（编程题1（优美的数字））
c++·算法·整除·枚举算法·求余·拆数
carver w2 小时前
MFC入门教程 最简版
c++·mfc
王老师青少年编程2 小时前
信奥赛C++提高组csp-s之倍增算法
c++·csp·信奥赛·csp-s·提高组·倍增算法·rmq
低频电磁之道2 小时前
编译C++的几种方式（MSVC编译器）
开发语言·c++
Zsy_0510033 小时前
【C++】类和对象（一）
开发语言·c++
Zevalin爱灰灰3 小时前
现代控制理论——第二章 系统状态空间表达式的解
线性代数·算法·现代控制
菜鸟233号3 小时前
力扣377 组合总和 Ⅳ java实现
java·数据结构·算法·leetcode
我是大咖3 小时前
二级指针与指针数组搭配
c语言·数据结构·算法
是娇娇公主~3 小时前
工厂模式详细讲解
数据库·c++
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03Claude Code Skills 实用使用手册04Labelme从安装到标注：零基础完整指南052025年大语言模型技术全景报告06AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08UV安装并设置国内源09网站改了域名，如何查找？10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）