
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 拼数](#1. 拼数)
[2. Protecting the Flowers S](#2. Protecting the Flowers S)
[3. 奶牛玩杂技](#3. 奶牛玩杂技)
推公式
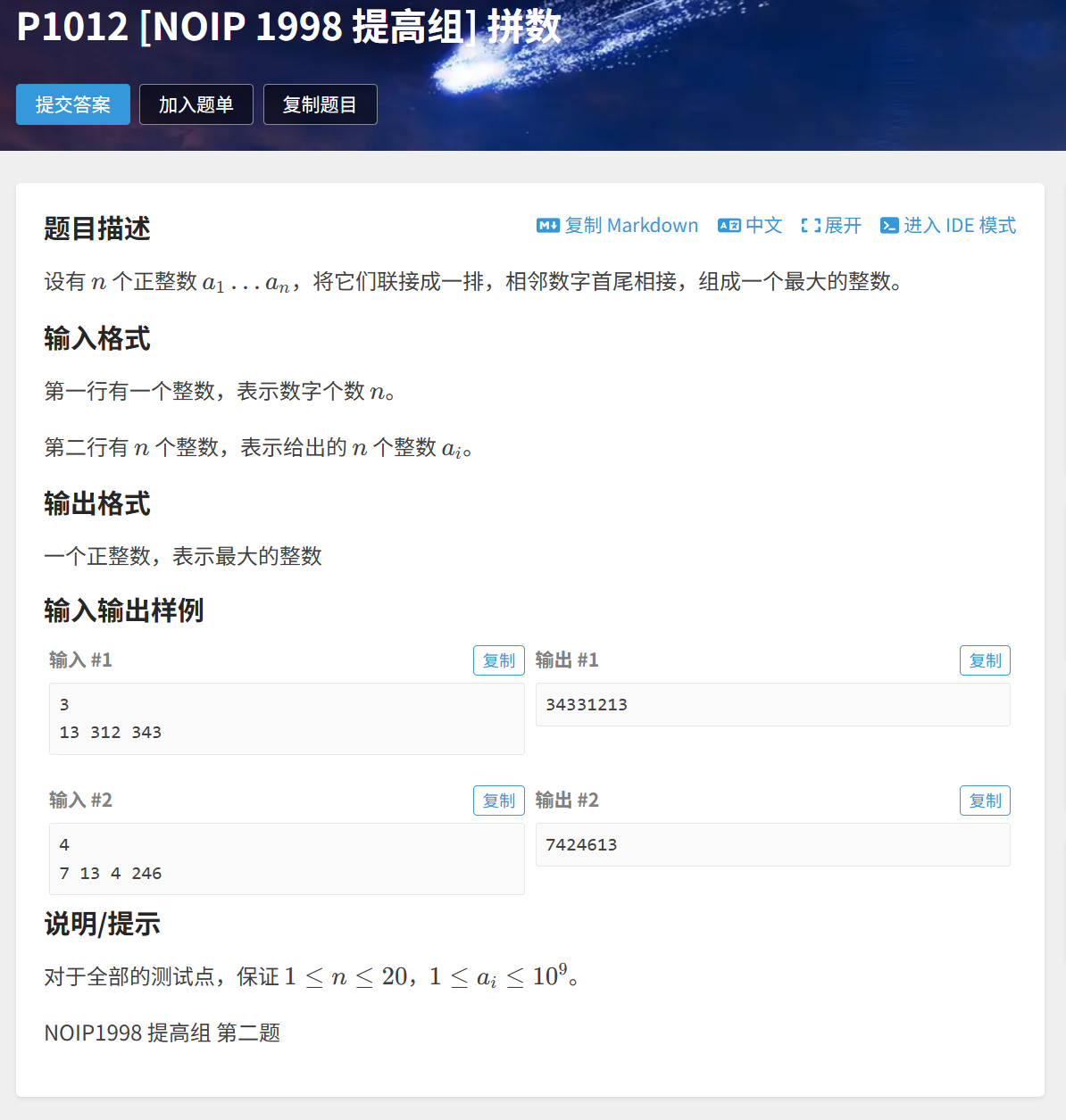
1. 拼数
题目链接:
算法原理
贪心算法:
我们定义 x + y = xy,例如 13 + 312 = 13312,312 + 13 = 31213
然后对数据进行排序
-
如果x + y > y + x,那么x放在前面,y放在后面
-
如果x + y < y + x,那么y放在前面,x放在后面
3 如果x + y = y + x,那么谁放在前面都无所谓
实操代码
cpp
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
bool compare(const string& a, const string& b) {
return a + b > b + a;
}
int main()
{
vector<string> v;
int n; cin >> n;
while (n--)
{
string s; cin >> s;
v.push_back(s);
}
sort(v.begin(), v.end(),compare);
string ret;
for (auto& it : v)
{
ret += it;
}
cout << ret;
return 0;
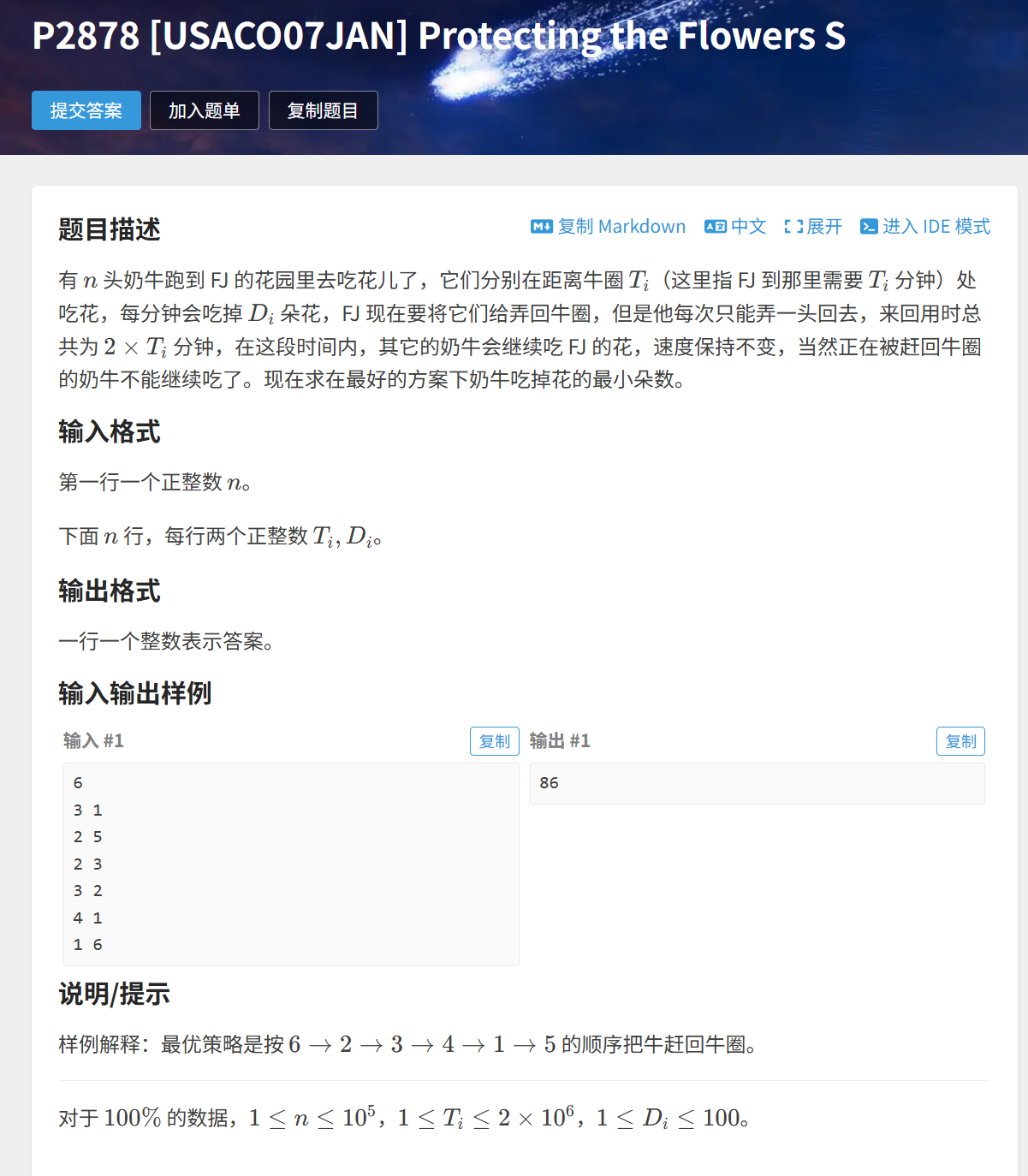
}2. Protecting the Flowers S
题目链接:
算法原理
贪心算法:
我们对原数组排序,排完序后的顺序就是最优的选择顺序
排序原则:
我们设交换i和j两头牛的位置,当从头开始到达i位置时,花费的时间为T
交换前:
第i头牛吃草量 T * di
第j头牛吃草量 T * (2 * ti) * dj
则总吃草量 sum1 = T * di + T * dj + 2 * ti * dj
交换后:
第j头牛吃草量 T * dj
第i头牛吃草量 T * (2 * tj) * di
则总吃草量 sum2 = T * dj + T* di + 2 * tj * di
因此如果要让i在j前面,则sum1 < sum2,即ti * dj < tj * di,反之在后面
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> T;
vector<int> D;
vector<int> v;
bool cmp(const int& x, const int& y)
{
return T[x] * D[y] < T[y] * D[x];
}
int main()
{
int n; cin >> n;
long long sum = 0;
long long ret = 0;
for (int i = 0; i < n; i++)
{
int t, d; cin >> t >> d;
T.push_back(t);
D.push_back(d);
v.push_back(i);
sum += d;
}
sort(v.begin(), v.end(),cmp);
for (auto& it : v)
{
sum -= D[it];
ret += sum * T[it];
}
cout << ret * 2;
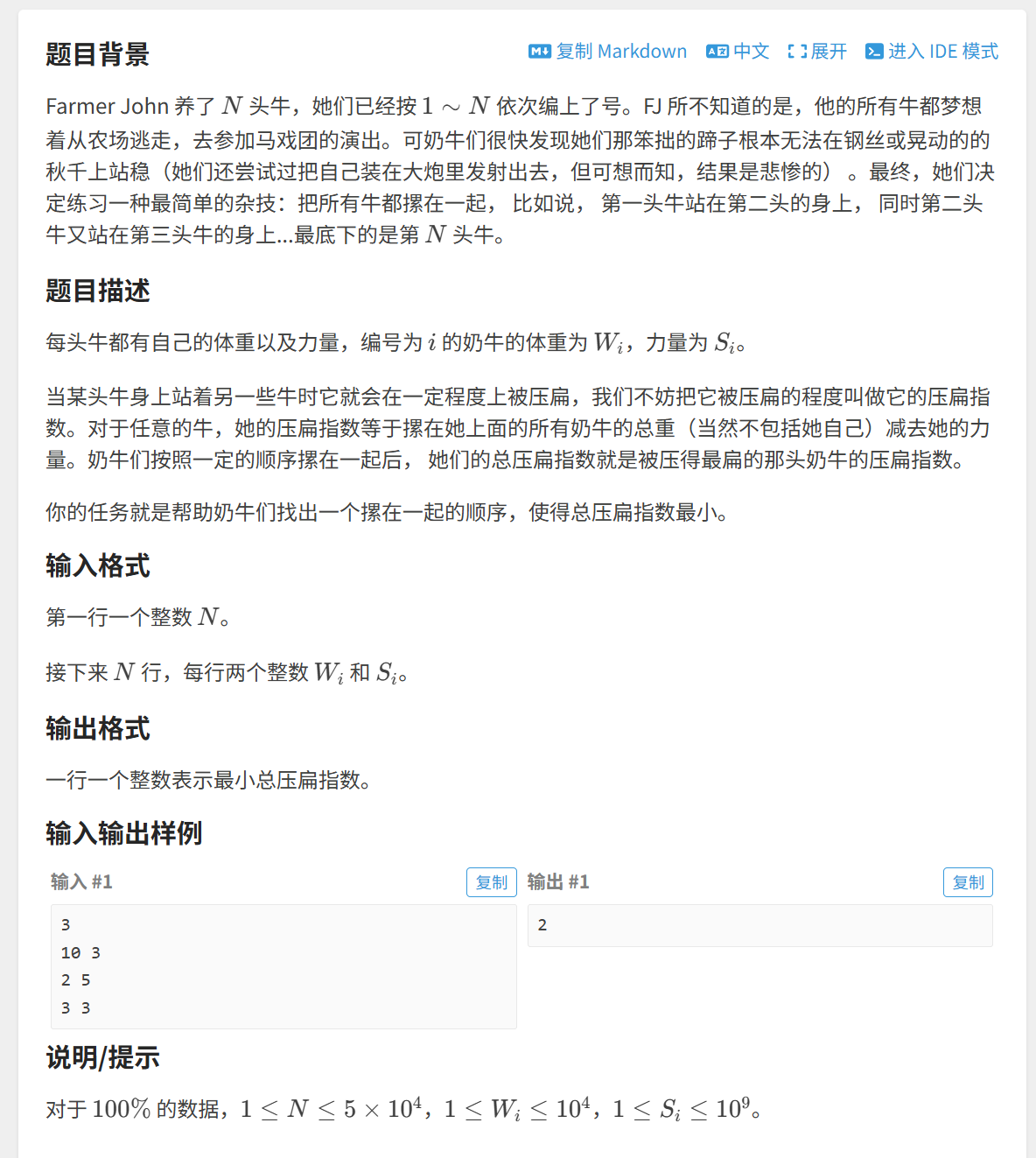
}3. 奶牛玩杂技
题目链接:
算法原理
贪心算法:
我们对原数组排序,排完序后的顺序就是最优的选择顺序(从下到上)
排序原则:
我们设交换i和j两头牛的位置,i前面的牛的总重为W
交换前:
第i头牛的压扁指数 W - si
第j头牛的压扁指数 W + wi - sj
则两头牛最大的压扁指数 k1 = max(W - si,W + wi - sj)
同理交换后最大的压扁指数k2 = max(W - sj,W + wj - si)
如果要满足i在j前面,则需满足k1 < k2,反之i在后面
实操代码
cpp
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 5e4 + 10;
int n;
struct node
{
int w, s;
}a[N];
bool cmp(node& i, node& j)
{
return i.w + i.s < j.w + j.s;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
cin >> a[i].w >> a[i].s;
sort(a + 1, a + 1 + n, cmp);
LL ret = -1e9 - 10, w = 0;
for(int i = 1; i <= n; i++)
{
ret = max(ret, w - a[i].s);
w += a[i].w;
}
cout << ret << endl;
return 0;
}