视频讲解:GESP2025年9月四级C++真题讲解
一、单选题
第1题

解析:
答案B,
int a = 42; //a变量存储42
int* p = &a; //指针p指向a变量地址
*p = *p + 1; //指针p地址的值 = 指针p地址的值 + 1 = 42 + 1 = 43第2题

解析:
答案C,
cpp
//A选项
int arr1[20];
cout<<arr1;//输出arr1[0]的地址
//B选项
int arr2[30];
cout<<arr2[17];//可以随机访问某一个
//C选项
int arr3[40];
arr3++;//会报错
//D选项
int arr[50];
cout<<sizeof(arr);//输出200,int(4字节)*数组大小(50)=200 第3题

解析:
答案D,
*(arr+1) 代表 arr[1][0]的地址
*( *(arr+1) +2 ) 代表 arr[1][2]的地址,即6第4题

解析:
答案A,
add(2)只传递了a=2,b为默认的1,所以return a+b; 结果为3
add(2,3)只传递了a=2,b=3,所以return a+b; 结果为5第5题

解析:
答案D,

第6题
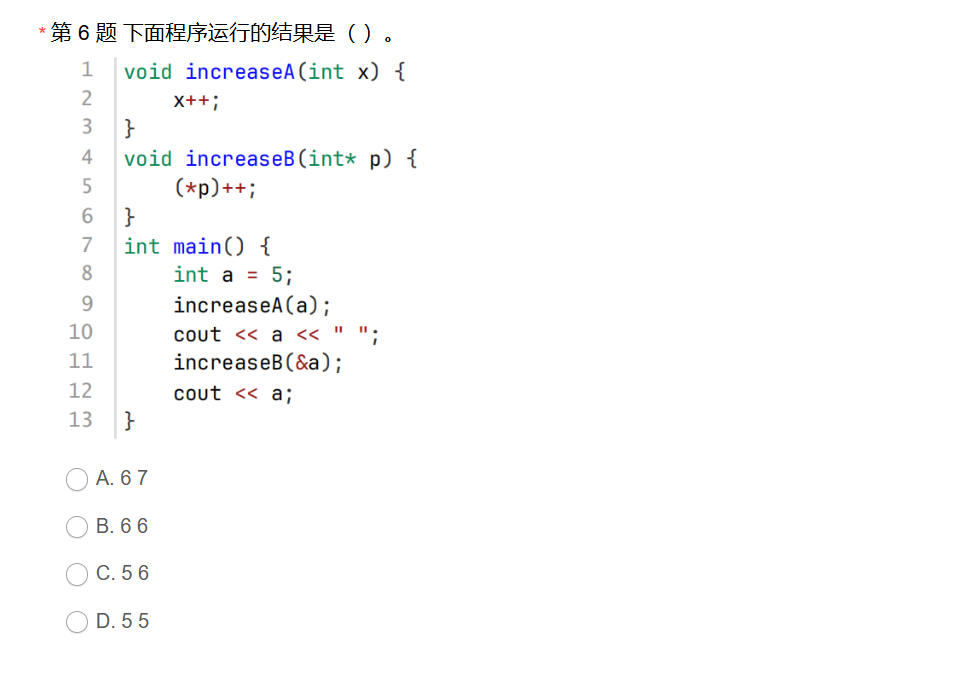
解析:
答案C,

第7题

解析:
答案B,结构体初始化的写法是B选项
第8题

解析:
答案B,birthday()函数用了引用传递,实参改变,所以age是3,name不变
第9题

解析:
答案C,选择、堆、快速、希尔排序都是不稳定的
第10题

解析:
答案A,升序,有人比它小才抢过来,所以num[s] < nums[minIndex]
第11题

解析:
答案A,arr[j] 代表比较位,key代表当前位,升序时:当前位 < 比较位 时,就前移,所以arr[j] < key。如果条件(当前位 < 比较位)不符合,当前位插入比较位的后面,所以arr[j+1] = key
第12题

解析:
答案B,插入排序最好的情况是O(n) , 最坏O(n²)
第13题

解析:
答案B,斐波那契数列
第14题

解析:
答案C,模拟出枚举代码,三层循环n次的嵌套循环,即时间复杂度n*n*n
cpp
int n=999;
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
for(int k=j+1;k<=n;k++){
}
}
}第15题

解析:
答案D,程序没有异常就不会被捕获,例如以下程序,b不一定为0
cpp
int divide(int a, int b) {
if(b == 0) throw "Division by zero";
return a / b;
}
int main() {
int result = 0;
try {
result = divide(10, 0);
cout << "A";
}
catch(const char* msg) {
cout << "B";
result = -1;
}
cout << result;
return 0;
}二、判断题
第1题

解析:
答案×,
bash
指针应该指向地址
int *p = &a;第2题

解析:
答案×,

第3题
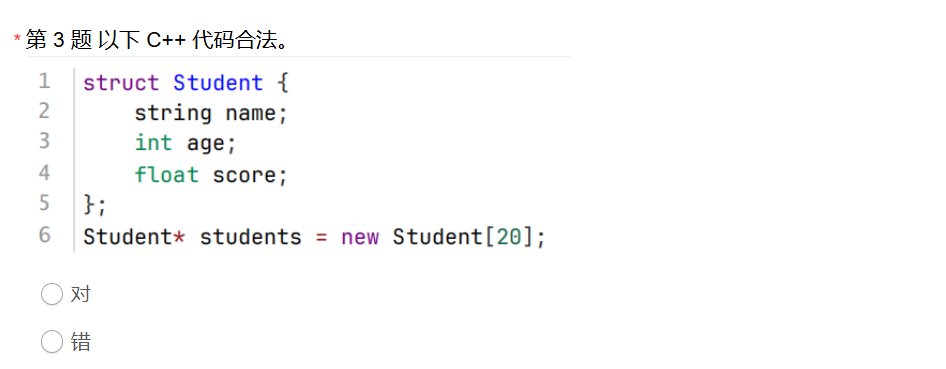
解析:
答案√,
cpp
//指针创建数组
int *arr = new int[20]
//结构体指针创建数组
student* arr = new student[20]第4题

解析:
答案√,指针传递改变实参
第5题

解析:
答案×,可以这样写,传递的是arr[0][0] 、 arr[0][1] 、 arr[0][2] 、 arr[0][3]
第6题

解析:
答案√,例如斐波那契数列
第7题

解析:
答案√,插入排序适合数据量小,且接近有序的数据
第8题

解析:
答案×,
cpp
初始的状态:4 1 3 1 5 2
第1次比较:(4 1) 3 1 5 2
第2次比较:1 (4 3) 1 5 2
第3次比较:1 3 (4 1) 5 2
第4次比较:1 3 1 (4 5) 2
第5次比较:1 3 1 4 (5 2)
第一轮冒泡后:1 3 1 4 2 5第9题

解析:
答案×,throw 42,抛出的42确实是int类型,但是catch(...)可以捕获任何类型
cpp
#include<bits/stdc++.h>
using namespace std;
// 故意抛出不同类型异常的函数
void throwDifferentExceptions(int type) {
switch (type) {
case 1:
throw 100; // 抛出 int 类型异常
case 2:
throw "Division by zero"; // 抛出 const char* 类型异常
case 3:
throw string("Custom string exception"); // 抛出 string 类型异常
case 4:
throw 3.14159; // 抛出 double 类型异常
default:
cout << "No exception thrown" << endl;
}
}
int main() {
// 遍历测试4种不同类型的异常
for (int i = 1; i <= 4; i++) {
cout << "=== 测试抛出第 " << i << " 种类型异常 ===" << endl;
try {
throwDifferentExceptions(i);
}
catch (...) { // 兜底,捕获剩余所有未匹配的异常
cout << "捕获到其他类型异常" << endl;
}
}
return 0;
}第10题

解析:
答案×,fout才可以
三、编程题
第1题 [GESP202509 四级] 排兵布阵
题目描述
作为将军,你自然需要合理地排兵布阵。地图可以视为 n 行 m 列的网格,适合排兵的网格以 1 标注,不适合排兵的网格以 0 标注。现在你需要在地图上选择一个矩形区域排兵,这个矩形区域内不能包含不适合排兵的网格。请问可选择的矩形区域最多能包含多少网格?
输入格式
第一行,两个正整数 n,m,分别表示地图网格的行数与列数。
接下来 n 行,每行 m 个整数 ai,1,ai,2,...,ai,m,表示各行中的网格是否适合排兵。
输出格式
一行,一个整数,表示适合排兵的矩形区域包含的最大网格数。
输入输出样例
输入 #1
4 3
0 1 1
1 0 1
0 1 1
1 1 1输出 #1
4输入 #2
3 5
1 0 1 0 1
0 1 0 1 0
0 1 1 1 0输出 #2
3说明/提示
对于所有测试点,保证 1 ≤ n,m ≤ 12,0 ≤ ai,j ≤ 1。
答案
cpp
#include <bits/stdc++.h>
using namespace std;
int main() {
//1)确定矩阵大小n*m
int n,m;
cin>>n>>m;
//2)填充二维数组
int a[22][22];
int p_s[22][22]={};
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
//3)计算当前缀和
//当前缀和:+自身 1+ 上部分2 +左部分3 -重复2=4
p_s[i][j]=a[i][j]+p_s[i-1][j]+p_s[i][j-1]-p_s[i-1][j-1];
}
}
//4)枚举所有左顶点的坐标
int ans=0;
for(int l_i=1;l_i<=n;l_i++){
for(int l_j=1;l_j<=m;l_j++){
//5)枚举所有右顶点的坐标
for(int r_i=l_i;r_i<=n;r_i++){
for(int r_j=l_j;r_j<=m;r_j++){
//6)判断是否全为1
//1的数量 :大矩阵8 - 上矩阵3 - 左矩阵3 + 重复1= 3
int sum=p_s[r_i][r_j]-p_s[l_i-1][r_j]-p_s[r_i][l_j-1]+p_s[l_i-1][l_j-1];
//计算矩阵大小:
//高度:3右顶点i-2左顶点i+1=2
//宽度:5右顶点j-3左顶点j+1=3
int s=(r_i-l_i+1) * (r_j-l_j+1);
//判断 矩阵大小 == 1的数量
if( s == sum ){
// 找最大值
if( ans < s ) ans=s;
}
}
}
}
}
cout<<ans;
}第2题 [GESP202509 四级] 最长连续段
题目描述
对于 k 个整数构成的数组 [b1,b2,...,bk],如果对 1≤i<k 都有 bi+1=bi+1,那么称数组 b 是一个连续段。
给定由 n 个整数构成的数组 [a1,a2,...,an],你可以任意重排数组 a 中元素顺序。请问在重排顺序之后,a 所有是连续段的子数组中,最长的子数组长度是多少?
例如,对于数组 [1,0,2,4],可以将其重排为 [4,0,1,2],有以下 10 个子数组:
4\],\[0\],\[1\],\[2\],\[4,0\],\[0,1\],\[1,2\],\[4,0,1\],\[0,1,2\],\[4,0,1,2
其中除 [4,0],[4,0,1],[4,0,1,2] 以外的子数组均是连续段,因此是连续段的子数组中,最长子数组长度为 3。
输入格式
第一行,一个正整数 n,表示数组长度。
第二行,n 个整数 a1,a2,...,an,表示数组中的整数。
输出格式
一行,一个整数,表示数组 a 重排顺序后,所有是连续段的子数组的最长长度。
输入输出样例
输入 #1
4
1 0 2 4输出 #1
3输入 #2
9
9 9 8 2 4 4 3 5 3输出 #2
4说明/提示
对于 40% 的测试点,保证 1 ≤ n ≤ 8。
对于所有测试点,保证 1 ≤ n ≤ ,−
≤ ai ≤
。
答案
cpp
#include <bits/stdc++.h>
using namespace std;
int main() {
//1)确定数量n
int n;
cin>>n;
//2)填充一维数组
int a[100010]={};
for(int i=1;i<=n;i++) cin>>a[i];
//3)排序 升序
sort(a+1,a+n+1);
//4)计算每个连续段
int len=1;
int ans=1;
for(int i=2;i<=n;i++){
//4.1)判断是否连续(差1) len++
if( a[i]-a[i-1]==1 ) len++;
//4.2)判断是否相同 不改变
else if( a[i]==a[i-1] ){
}else{//4.3)否则 判断找出最大值,len初始化为1
if(len>ans) ans=len;
len=1;
}
}
//解决最后一次无法触发判断
if(len>ans) ans=len;
cout<<ans;
}