本篇将详细介绍FHQ-Treap的核心思想以及代码实现
一:BST
BST是二叉搜索树,说白了就是一颗二叉树,它满足这样的性质:
对于任意节点x,它的左子树中的所有值都比x小,右子树中的所有值都比x大
(注意,我们正常情况下的BST是不允许有重复权值的点,一般会维护一个结构体,里面存一个cnt表示相同权值有多少个数,但我们这里讲BST实际是为了后面的平衡树,所以我们默认左右子树中可以存在等于的情况)
举一个例子:
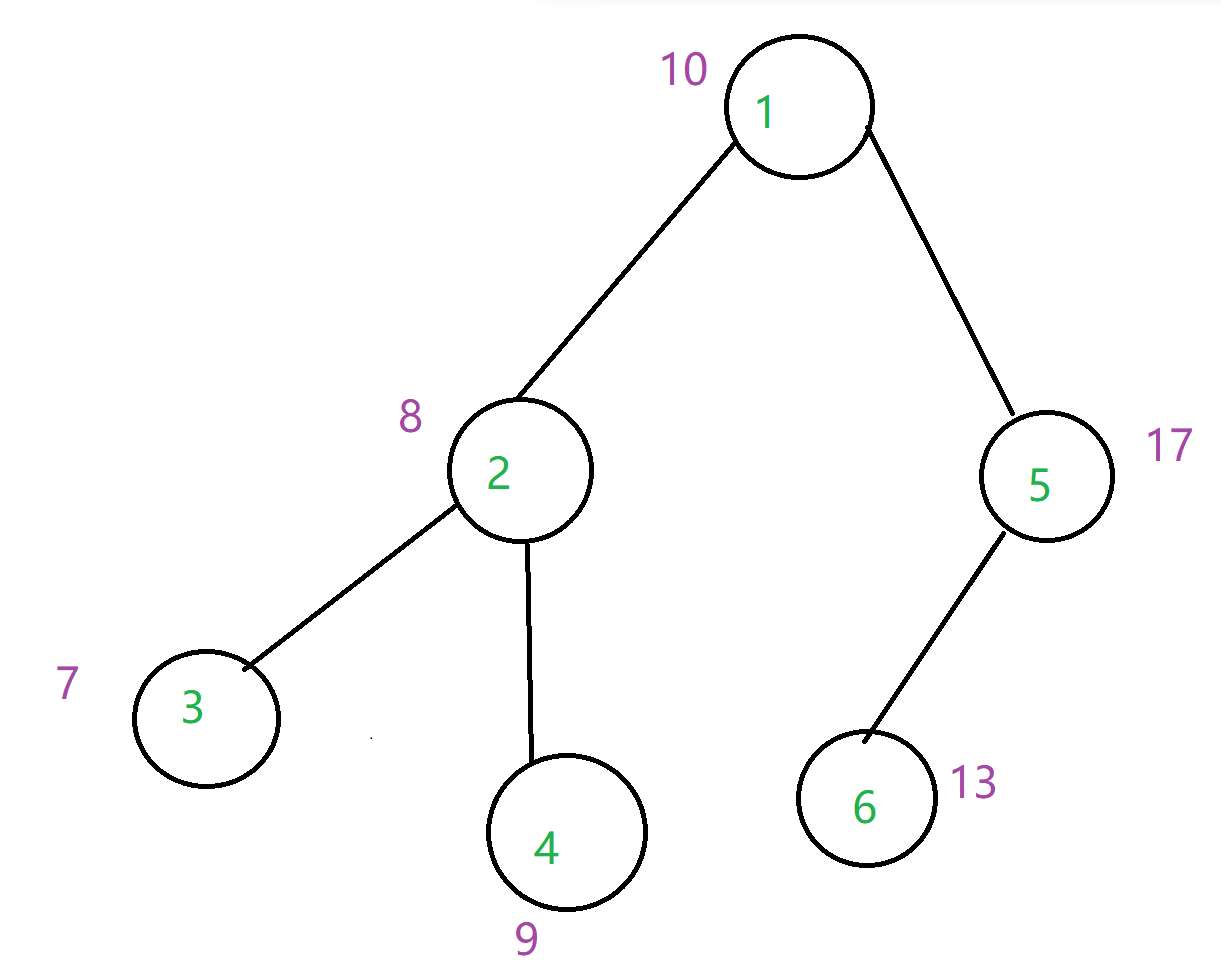
这颗树就是一颗标准的BST,符合BST的所有性质(绿是编号,紫是权值)
首先想要实现一个BST,我们需要维护以下信息
cpp
struct BST{
int ls,rs;//左右儿子编号
int sz;//子树大小
int val;//节点权值
int cnt;//相同权值个数(在FHQ-Treap中并不需要)
}; 我们考虑题目中的操作:
1):插入一个数x:
考虑x应该插入到哪里:如果有x出现了,那么直接找到这个位置,cnt+1。否则就要新建一个节点,我们考虑如何找到这个位置:
假设目前的点是k,那么有三种情况:
一:k的权值和x相等,或者点k根本不存在(等于0)
说明找到了合适的位置,直接插入即可
二:k的权值小于x
因为是BST,k的权值都小于x,k的左子树里的所有点的权值都小于k,那么它们自然也小于x,所以插到k或者k左子树都会使得破坏BST的结构,所以我们应该往k的右子树找
三:k的权值大于x
同理,k右子树的权值都大于x,所以x不能插到右边,只能往k的左子树去找
重复二,三的判断,不断递归,直到满足一,插入操作结束
具体代码如下
cpp
void insert(int k, int x) {
t[k].sz ++;
if(t[k].val == x){//若当前权值出现过,cnt++(满足1)
t[k].cnt ++;
return;
}
if (t[k].cnt == 0) { // 若当前权值未出现过,直接赋值为1 (满足一)
t[k] = {0, 0, 1, 1, x};
return;
}
if (t[k].val > x) { // 满足三
if (t[k].ls == 0) t[k].ls = ++cont; // 新建左孩子
insert(t[k].ls, x);
} else { // 满足二
if (t[k].rs == 0) t[k].rs = ++cont; // 新建右孩子
insert(t[k].rs, x);
}
}3):查询排名为x的数
我们考虑如果k的排名是x,那么可以说明,k左子树的sz +1为x
因为只有左子树的值<t[k].val,所以左子树多大,比k小的数就有几个,排名自然就是这个数+1
然后就很好办了:
假设目前点是k,查询排名是x的数
一:如果k左儿子的sz >= x的话,那么说明左子树里有>=x个数,答案一定在左子树内,继续查左子树排名为x的数
二:如果k的左儿子sz<x,但是左儿子的sz+k的cnt>=x,这说明什么,左子树内部没有x个数,但是左子树的大小加上k的大小居然>=x,很明显,答案就是k的val
比如我要查排名4的数,左儿子有3个数,自己的cnt是2,那说明自己就是排名第4的数
三:如果一,二都不成立,那么说明答案在右子树
这其实也解决了2)操作
具体代码如下:
cpp
int query_num_rank(int k, int x) {
if (t[t[k].ls].sz >= x) { // 左子树大小足够,在左子树中查询
return query_num_rank(t[k].ls, x);
} else if (t[t[k].ls].sz + t[k].cnt >= x) { // 当前节点即为目标
return t[k].val;
} else { // 需在右子树中查询,调整x为右子树中的相对排名
return query_num_rank(t[k].rs, x - t[t[k].ls].sz - t[k].cnt);
//x减去左子树和k的大小
}
}至于前驱和后继,BST和FHQ-Treap的实现不太相同,我们一会讲平衡树再说
二:FHQ-Treap
首先说一下为什么要引入平衡树这种东西呢:因为单纯的BST形态很不稳定,有可能被卡成一条链,所以这样的话,它的插入,删除等操作就达到了O(n)的复杂度,是令人无法忍受的
这里我们介绍的平衡树是FHQ-Treap,又叫非旋Treap,因为正常的Treap需要旋转操作,不好理解,于是我们更喜欢用这种平衡树
FHQ-Treap是自平衡二叉树,本质也是一颗BST,它不是通过严格的操作使得树的形态严格平衡,而是通过两个核心操作:split和merge来实现操作时的平衡,split是分裂,即把树按照权值拆成两个部分,一个部分的权值全部<=x,另一个部分权值全部>x。merge是合并,就是split的逆操作,不过也不是完全逆,具体下面说
1):split操作
我们考虑目前一颗完好的普通BST,那么我们以<=x为分界线,分出来的形状大概是长这样的
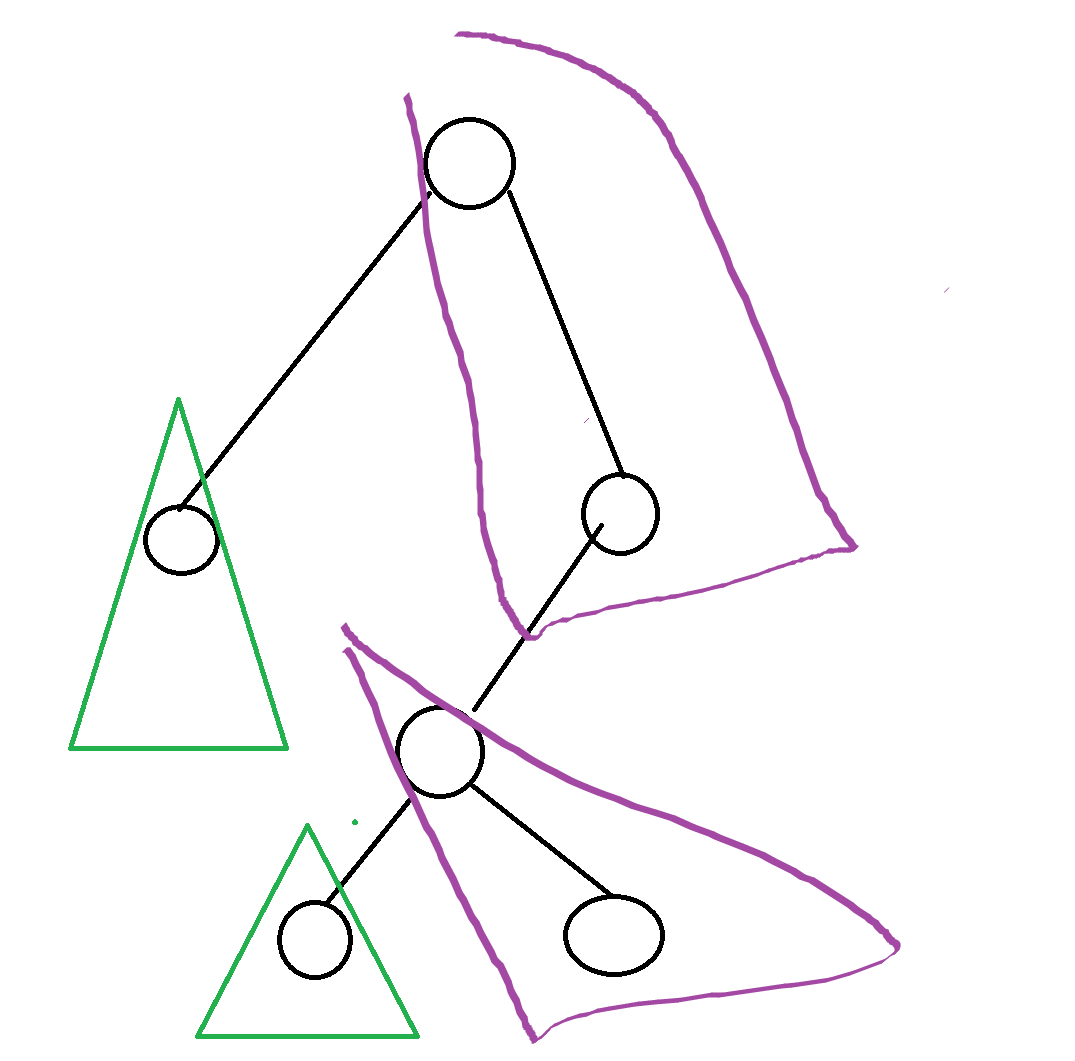
绿色的是<=x,紫色反之
那我们的split过程实际就是这样,我们要在这个过程中把紫色部分和绿色部分分开,并且把绿色部分,紫色部分内部连接起来,将一颗树按照x分成两颗树,绿色树里的值全部小于等于x,紫色树里的值全部大于x
代码如下,这个代码其实很不好理解
cpp
void split(int k,int &l,int &r,int val){
//l表示目前递归过程中,最近一颗"绿色树"的根节点,也就是最后一个<=val的点编号,r同理,val是分割值,k是当前点编号
if(!k) {
l = r = 0;
//如果这个点不存在,那么我们一定要清空引用标记
//因为这个位置的引用很有可能出自上一层的ls,rs,只有修改成0才能说明上一层的点根本没有这个儿子
return ;
}
if(t[k].val <= val) {
l = k;
//说明k是目前最后一个<=val的点, 那么更新l为k
split(t[k].rs,t[k].rs,r,val);//说明k及k左子树都被划为绿色树,我们继续划分k的右子树,r不变
//其实这也是一个连边,就是连接起来那些绿色树的过程
//因为我们的递归里,l位置传的是t[k].rs
// 也就是说,我们想要找到下面的绿色树,因为下面的绿色树一定会进入这个if的判断
//因为一旦进入这个判断,l值就会被修改为k,那么那个时候的l值就一定会被更改为那颗绿色树的根节点(k)
// 因为只要是绿色树,我们就只改变l的引用,所以下一次修改时,t[k].rs就自然等于下一颗绿色树的根节点了
//因为我们把这颗绿色树和下一颗绿色树连边了,而在此之前,下一颗绿色树也已经和下面的所有绿色树都连边,所以自下而上,绿色树就建好了
}
else{
r = k;//同理
split(t[k].ls,l,t[k].ls,val);
}
}其实就是一边判断这个点左右子树的划分情况(分到绿色树还是紫色树),一边连接绿色和紫色树,使它们变成两颗完好的树
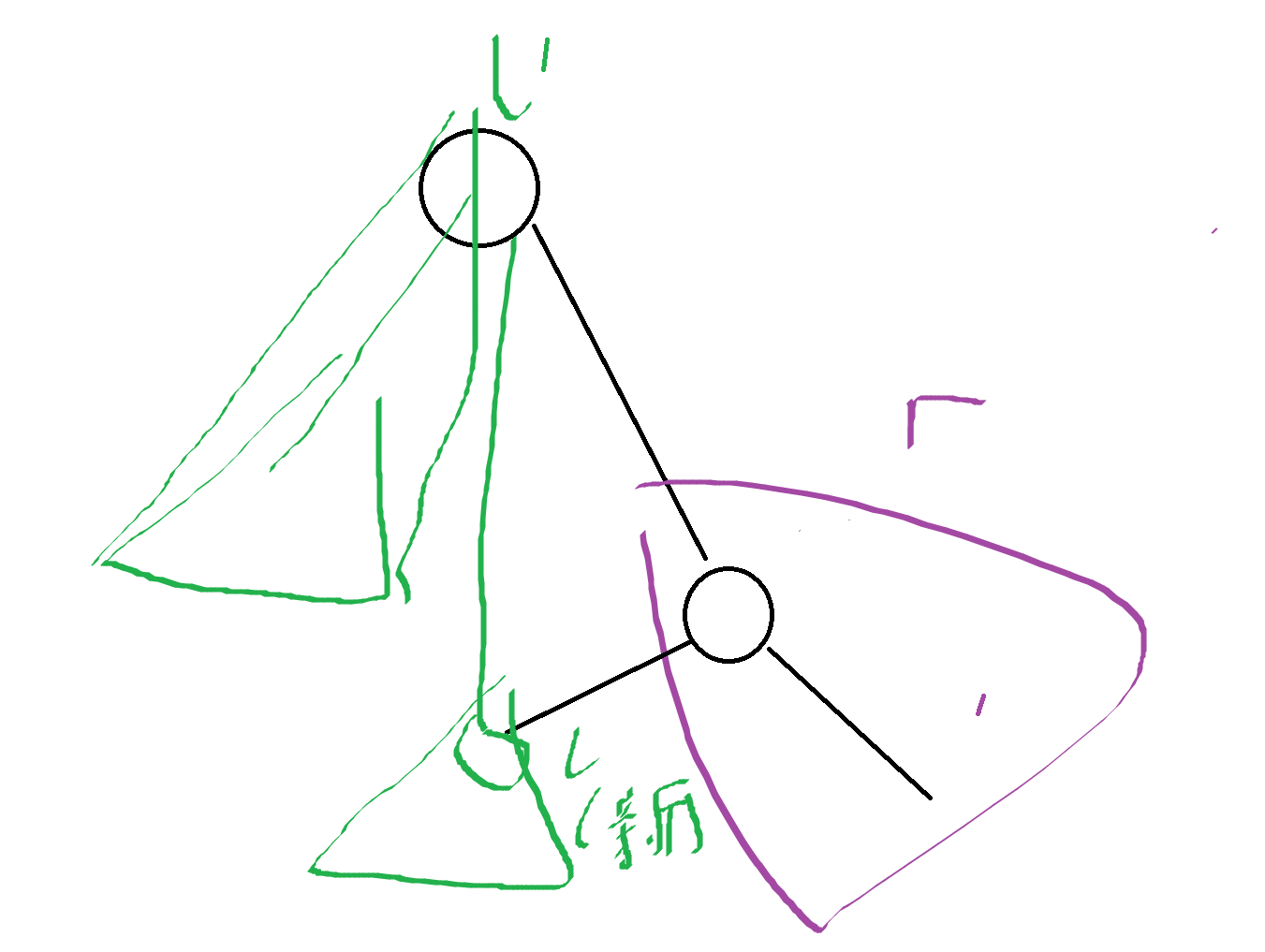
过程大概就是这样
2):merge操作
这里有一个精髓,我们为了不让树过高导致被卡成一条链,而我们也不想有太复杂的操作,于是我们引入了双重权值:即每个点的权值不止有val还有一个key,这个key的值我们随机赋。split是按照val分裂,而merge是按照key的大小优先合并,也就是说这颗树,split之后,它只满足val值符合BST性质,而key值是随机打乱的(我们刚才的代码里也完全没有key)
而merge之后,它同时满足val,key均符合BST的性质
这里的merge函数是int类型的,它返回的值就是两棵树合并之后的根节点编号
假设目前有两颗树进行merge,第一颗树目前的点是l,第二颗树目前点是r
1):l为空或r为空
那么很显然,以这两个点为根的子树,由于其中一颗是空的,所以合并结果完全是另一颗子树,根节点也就是非0那个(也有可能都是0,那么两颗子树全都是空的,合并结果也是空的)
2):l的key<=r的key
根据BST的性质,我们让key更小的当根,即让r为根的子树和l的右子树继续合并,而l的左子树不变,也就是此时l子树和r子树合并后,这棵树的根是l,把r子树接到l的右子树内部
3):l的key>r的key
同理,把r的左子树和l合并,r此时是根
于是merge操作就结束了,大概流程如下
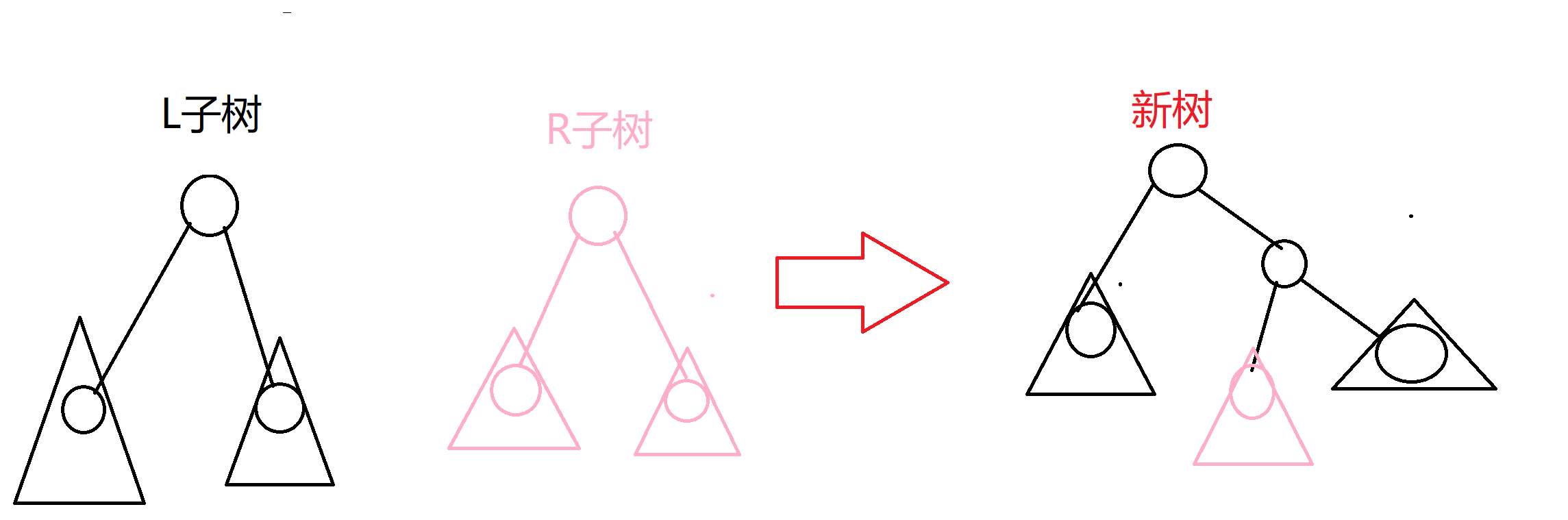
注意我们只是把一棵树接到另一颗树的一面,而不是直接变成左右儿子
而且这个过程中,我们发现我们完全没有进行val值的判断,所以merge前一定要保证这两颗树val值是严格l<r的
(其实你发现这个过程挺像线段树合并的)
具体代码如下,解释的很清晰了:
cpp
#include<bits/stdc++.h>
using namespace std;
#define _for(i,a,b) for(int i = (a) ; i <= (b) ; i ++)
#define for_(i,a,b) for(int i = (a) ; i >= (b) ; i --)
const int maxn = 1e5 + 10;
struct treap{
int ls,rs,val,key,sz;
}t[maxn];
mt19937 rnd;//随机数生成
int n,cnt,rt;
int newkey(int x){
t[++ cnt] = {0,0,x,rnd(),1};
//初始化
return cnt;//编号
}
void push_up(int k){
t[k].sz = t[t[k].ls].sz + t[t[k].rs].sz + 1;
//更新sz,k的sz就是左右子树的sz和加上自己这个点
}
void split(int k,int &l,int &r,int val){
if(!k) {
l = r = 0;
return ;
}
if(t[k].val <= val) {
l = k;
split(t[k].rs,t[k].rs,r,val);
}
else{
r = k;
split(t[k].ls,l,t[k].ls,val);
}
push_up(k);
}
int merge(int l,int r){
if(!(l && r)) return l + r;
//简化写法,一个是0,相加结果就是不是0那个的编号
if(t[l].key <= t[r].key) {
t[l].rs = merge(t[l].rs,r);//l的右儿子更新为r树和l原本右子树合并后的根节点
push_up(l);
return l;//这部分树根是l
}
else {
t[r].ls = merge(l,t[r].ls);
push_up(r);
return r;
}
}
int kth(int k,int sz){//排名为sz的节点编号,具体和BST没区别,不讲了
if(t[t[k].ls].sz + 1 == sz) return k;
else if(t[t[k].ls].sz + 1 < sz) return kth(t[k].rs, sz - t[t[k].ls].sz - 1);
else return kth(t[k].ls,sz);
}
int main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T;
cin >> T;
while(T --){
int op;
cin >> op;
if(op == 1){
int x;
cin >> x;
int p = newkey(x);//获取编号和初始化
int l = 0,r = 0;
split(rt,l,r,x);
rt = merge(merge(l,p),r);
//因为要插入一个数,于是我们按照这个数 把树分成两部分,再把左子树和这个点合并一下,得到的新树再和右子树合并
}
else if(op == 2){
int x;
cin >> x;
int l = 0,r = 0,lr = 0;
//我们想要删除一个x,那我们就得找到一颗全是x的树
split(rt,l,r,x);
//先按照x分成两部分
split(l,l,lr,x - 1);//注意l为根
//然后在原本的左子树,按照x-1分成两部分 ,这样新的左子树就是<=x-1的,右子树就是等于x的
int y = merge(t[lr].ls,t[lr].rs);
rt = merge(merge(l,y),r);
//删除这个点,那么直接把它的左右子树合并即可,因为只删一个,所以不用把整颗=x的树都删了
}
else if(op == 3){
int x;
cin >> x;
int l = 0,r = 0;
split(rt,l,r,x - 1);
//按照x-1分,<=x-1的是左子树
//那么排名就是左子树大小+1
cout << t[l].sz + 1 << '\n';
rt = merge(l,r);
}
else if(op == 4){
int x;
cin >> x;
cout << t[kth(rt,x)].val << '\n';
//先查排名为x的编号,然后输出这个编号对应的val
}
else if(op == 5){
//前驱实际是<=x-1中最大的一个,那我们直接按照x-1 split
//左子树中最大的数,也就是排名为sz的数即为前驱
int x;
cin >> x;
int l = 0,r = 0;
split(rt,l,r,x - 1);
int pm = kth(l,t[l].sz);
cout << t[pm].val << '\n';
rt = merge(l,r);
}
else {
int x;
cin >> x;
int l = 0,r = 0;
split(rt,l,r,x);
int pm = kth(r,1);
cout << t[pm].val << '\n';
rt = merge(l,r);
}
}
return 0;
}这里注意每次split之后一定要merge,要不然树都断了
然后这里main的l,r都是表示绿色树,紫色树的根节点
不知道你有没有一个问题(反正我学的时候是遇到了):
为什么main的l,r是根节点呢?split里的l,r明明是最后一个,为什么main函数里是第一个呢?
其实观察split,当我们传引用,比如原本传的是l,现在传的是t[k].rs,那么原本的l就不会随着t[k].rs改变了,而如果原本是l现在传的还是l,那么会随着继续递归,l值被改变
我们发现,只要第一次l或者r的引用变了,从split(l)变成split(t[k])之后,main函数里的l,r就不会继续随着改变了,也就是只有第一次改变,那么自然而然,lr分别是绿色树,紫色树的根节点了。