目录
[六、14 天打球示例在算什么?](#六、14 天打球示例在算什么?)
[七、ID3、C4.5、CART 在干什么?](#七、ID3、C4.5、CART 在干什么?)
[十一、随机森林:Bagging 的代表](#十一、随机森林:Bagging 的代表)
一、什么是决策树?
决策树是一种树模型。
它的工作方式是:
从根节点开始,根据特征一步一步往下判断,
最终走到叶子节点,得到一个决策结果。
所有数据最终都会落到某一个叶子节点,因此:
-
决策树可以做 分类
-
也可以做 回归
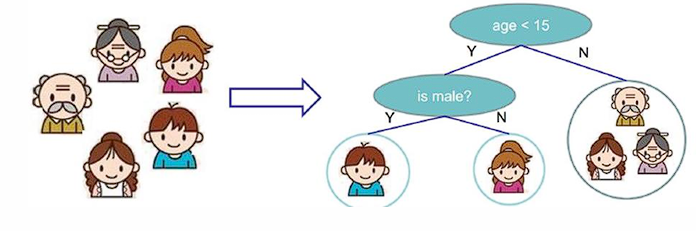
决策树就是把"人做决定的过程"画成了一棵树,本质是多层 if-else。
二、训练和预测分别在做什么?
-
训练阶段:从训练数据中构造一棵树
-
测试阶段:对新样本从上到下走一遍即可
真正难的是:
第一步问什么?
第二步再问什么?
问到什么时候停?
三、为什么要"选最好的特征"?
决策树训练时,每一层都要回答一个问题:
当前节点,用哪个特征来切分数据最合适?
目标是:
一刀下去,让数据尽可能"分清楚"
四、熵:衡量"乱不乱"的指标
文档中引入了熵,用来衡量数据的不确定性。
熵的定义是:
-
类别越杂,越混乱,熵越大
-
类别越单一,越纯净,熵越小
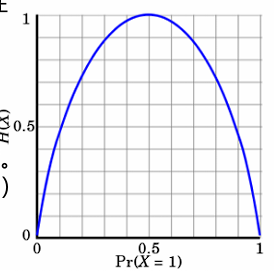
极端情况:
当p = 0或 p = 1时,H(p)=0,随机变量完全没有不确定性
当p = 0.5时,H(p)=1,此时随机变量的不确定性最大
五、信息增益:决定谁当"老大"
信息增益的思想是:
一个特征切分之后,让系统的不确定性减少了多少
本质公式是:
人话解释
-
切之前有多乱
-
切之后还剩多乱
-
差值越大,说明这个特征越"会分"
信息增益最大的特征,用作根节点
六、14 天打球示例在算什么?
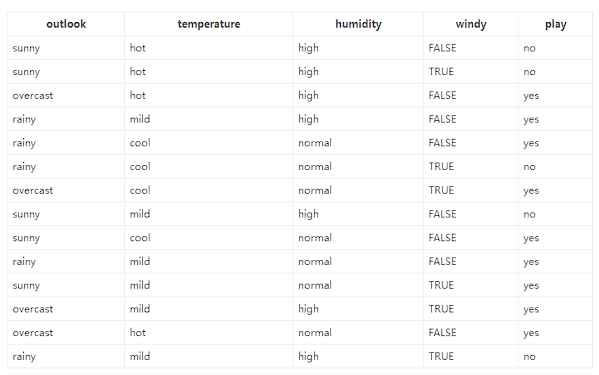
数据
-
14 天是否打球
-
4 个特征:天气、温度、湿度、风
-
目标:是否打球
原始数据中:
-
9 天打球
-
5 天不打球
原始熵为:
决策树构造实例
划分方式:4种
问题:谁当根节点呢?
依据:信息增益
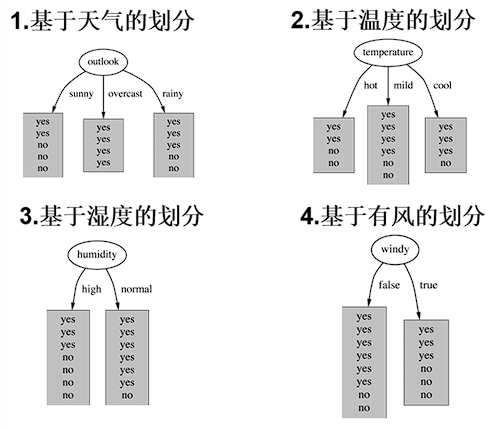
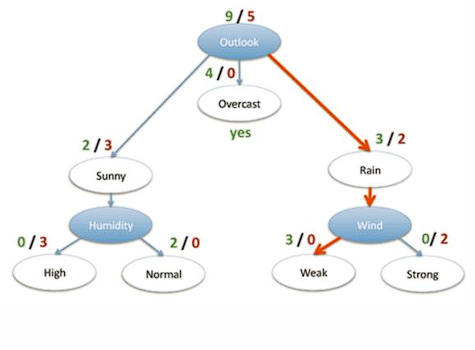
以"天气"特征为例
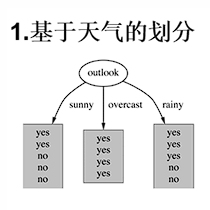
分裂后加权熵为:
信息增益为:
4个特征逐一分析,先从outlook特征开始:
Outlook = sunny时,熵值为0.971
Outlook = overcast时,熵值为0
Outlook = rainy时,熵值为0.971
天气这个特征,一下子把"能不能打球"分得更清楚,所以它胜出。
七、ID3、C4.5、CART 在干什么?
三种决策树算法:
-
ID3:信息增益
-
C4.5:信息增益率
-
CART:GINI 系数
GINI 系数定义为:
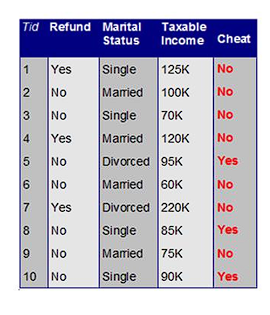
八、连续值怎么切?
对于连续特征(如年龄、收入):
处理流程是:
-
排序
-
枚举切分点
-
计算每个切分点的指标
-
选择最优切分点
九、为什么一定要剪枝?
如果不限制:
决策树可以一直长,
直到每个叶子节点只剩一个样本。
这会导致严重的过拟合。
剪枝方式
-
预剪枝:限制深度、叶子节点样本数
-
后剪枝:建完树再剪
后剪枝目标函数为:
十、集成学习:一个模型不够怎么办?
集成学习的核心思想是:
单个模型容易犯错,一群模型更稳
主要包括:
-
Bagging
-
Boosting
-
Stacking
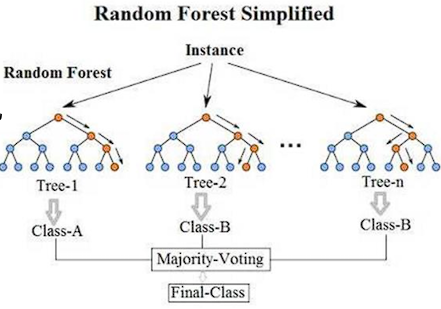
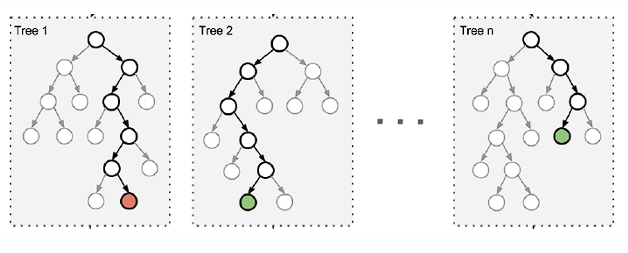
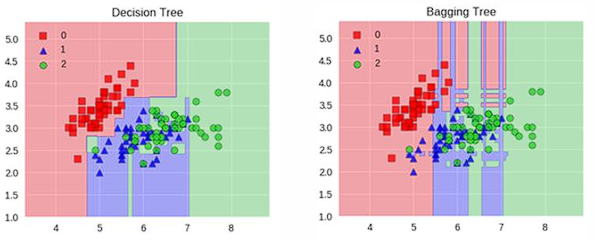
十一、随机森林:Bagging 的代表
随机森林的关键是 两层随机性:
-
数据随机采样
-
特征随机选择
目的只有一个:
让每棵树都不一样
十二、Boosting:专门盯着"错题本"
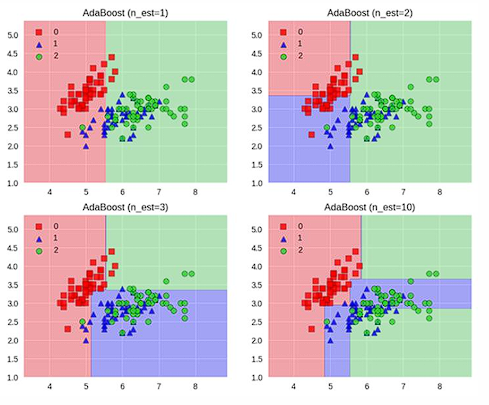
Boosting 的核心思想是:
分错的样本,在下一轮获得更大的权重
最终结果是多个弱学习器按权重加权组合。
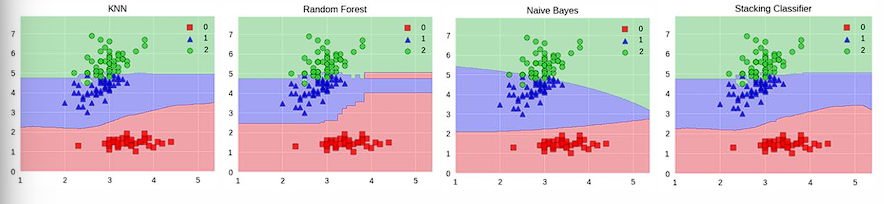
十三、Stacking:暴力但有效
Stacking 的做法是:
-
第一阶段:多个模型各自预测
-
第二阶段:用这些预测结果再训练一个模型
优点:准确率高
缺点:训练慢、结构复杂
总结
-
决策树直观、易解释,但容易过拟合
-
集成算法通过"群体智慧"提升泛化能力
-
随机森林与 Boosting 是工程与竞赛中的常用武器