LeetCode 2975.移除栅栏得到的正方形田地的最大面积：暴力枚举所有可能宽度

【LetMeFly】2975.移除栅栏得到的正方形田地的最大面积：暴力枚举所有可能宽度

力扣题目链接：https://leetcode.cn/problems/maximum-square-area-by-removing-fences-from-a-field/

有一个大型的 (m - 1) x (n - 1) 矩形田地，其两个对角分别是 (1, 1) 和 (m, n) ，田地内部有一些水平栅栏和垂直栅栏，分别由数组 hFences 和 vFences 给出。

水平栅栏为坐标 (hFences[i], 1) 到 (hFences[i], n)，垂直栅栏为坐标 (1, vFences[i]) 到 (m, vFences[i]) 。

返回通过移除一些栅栏（可能不移除 ）所能形成的最大面积的正方形 田地的面积，或者如果无法形成正方形田地则返回 -1。

由于答案可能很大，所以请返回结果对 10⁹ + 7 取余后的值。

注意： 田地外围两个水平栅栏（坐标 (1, 1) 到 (1, n) 和坐标 (m, 1) 到 (m, n) ）以及两个垂直栅栏（坐标 (1, 1) 到 (m, 1) 和坐标 (1, n) 到 (m, n) ）所包围。这些栅栏不能被移除。

示例 1：

复制代码

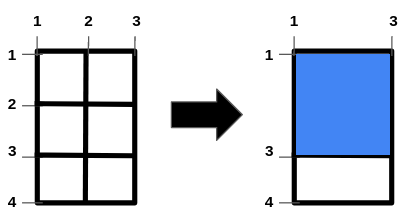
输入：m = 4, n = 3, hFences = [2,3], vFences = [2]
输出：4
解释：移除位于 2 的水平栅栏和位于 2 的垂直栅栏将得到一个面积为 4 的正方形田地。

示例 2：

复制代码

输入：m = 6, n = 7, hFences = [2], vFences = [4]
输出：-1
解释：可以证明无法通过移除栅栏形成正方形田地。

提示：

3 <= m, n <= 10⁹
1 <= hFences.length, vFences.length <= 600
1 < hFences[i] < m
1 < vFences[i] < n
hFences 和 vFences 中的元素是唯一的。

解题方法：暴力枚举

水平竖直单看一个方向，可能的边长有哪些？

任意两个栅栏之间的距离都可以是边长，可以二重循环栅栏位置并将其放入哈希表中。

水平竖直一块看，如果一个边长在水平方向有可能得到，在竖直方向也有可能得到，那么就有办法得到这个长度为边长的正方形。

也就是两个哈希表求个交并取最大就好了。

时间复杂度 O ( ( l e n ( h F e n c e s ) + l e n ( v F e n c e s ) ) 2 ) O((len(hFences) + len(vFences))^2) O((len(hFences)+len(vFences))2)，这是因为 ( a + b ) 2 = a 2 + b 2 + 2 a b (a+b)^2=a^2+b^2+2ab (a+b)2=a2+b2+2ab，复杂度中等于 a 2 + b 2 + a b a^2+b^2+ab a2+b2+ab
空间复杂度 O ( l e n ( h F e n c e s ) + l e n ( v F e n c e s ) ) O(len(hFences) + len(vFences)) O(len(hFences)+len(vFences))

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2026-01-17 21:08:43
 */
class Solution {
private:
    unordered_set<int> get(int n, vector<int>& v) {
        v.push_back(1);
        v.push_back(n);
        unordered_set<int> ans;
        for (int i = 0; i < v.size(); i++) {
            for (int j = i + 1; j < v.size(); j++) {
                ans.insert(abs(v[i] - v[j]));
            }
        }
        return ans;
    }
public:
    int maximizeSquareArea(int m, int n, vector<int>& hFences, vector<int>& vFences) {
        unordered_set<int> va = get(m, hFences), vb = get(n, vFences);
        int side = 0;
        for (int a : va) {
            if (vb.count(a)) {
                side = max(side, a);
            }
        }
        return side ? (long long) side * side % 1000000007 : -1;
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源