【数据结构】二叉树：从基础到应用全面解析

Remember_9932026-01-18 8:36

目录

一、树型结构基础

[1.1 树的基本概念](#1.1 树的基本概念)

[1.2 树的重要术语（面试常考）](#1.2 树的重要术语（面试常考）)

[1.3 树的表示方法](#1.3 树的表示方法)

[1.3.1 孩子兄弟表示法（最常用）](#1.3.1 孩子兄弟表示法（最常用）)

[1.3.2 孩子表示法（每个节点存储所有孩子）](#1.3.2 孩子表示法（每个节点存储所有孩子）)

[1.4 树的应用场景](#1.4 树的应用场景)

二、二叉树核心概念

[2.1 二叉树的定义](#2.1 二叉树的定义)

[2.2 特殊二叉树类型](#2.2 特殊二叉树类型)

[2.2.1 满二叉树 (Full Binary Tree)](#2.2.1 满二叉树 (Full Binary Tree))

[2.2.2 完全二叉树 (Complete Binary Tree)](#2.2.2 完全二叉树 (Complete Binary Tree))

[2.2.3 二叉搜索树 (BST) - 重要补充](#2.2.3 二叉搜索树 (BST) - 重要补充)

[2.2.4 平衡二叉树 (AVL Tree) - 重要补充](#2.2.4 平衡二叉树 (AVL Tree) - 重要补充)

[2.2.5 红黑树 (Red-Black Tree) - 重要补充](#2.2.5 红黑树 (Red-Black Tree) - 重要补充)

[2.3 二叉树的重要性质（必背公式）](#2.3 二叉树的重要性质（必背公式）)

[2.4 二叉树的存储结构](#2.4 二叉树的存储结构)

[2.4.1 链式存储（最常用）](#2.4.1 链式存储（最常用）)

[2.4.2 顺序存储（数组表示）](#2.4.2 顺序存储（数组表示）)

三、二叉树的遍历算法

[3.1 深度优先遍历 (DFS)](#3.1 深度优先遍历 (DFS))

[3.1.1 递归遍历（基础）](#3.1.1 递归遍历（基础）)

[3.1.2 非递归遍历（迭代，面试常考）](#3.1.2 非递归遍历（迭代，面试常考）)

[3.1.3 莫里斯遍历 (Morris Traversal) - 空间复杂度O(1)](#3.1.3 莫里斯遍历 (Morris Traversal) - 空间复杂度O(1))

[3.2 广度优先遍历 (BFS) / 层序遍历](#3.2 广度优先遍历 (BFS) / 层序遍历)

[3.3 遍历算法对比](#3.3 遍历算法对比)

四、二叉树基本操作实现

[4.1 节点统计操作](#4.1 节点统计操作)

[4.2 树的结构操作](#4.2 树的结构操作)

五、二叉树常见面试题深度解析

[5.1 最近公共祖先（LCA）问题扩展](#5.1 最近公共祖先（LCA）问题扩展)

[5.2 二叉树的直径问题](#5.2 二叉树的直径问题)

[5.3 二叉树的最大路径和](#5.3 二叉树的最大路径和)

六、二叉搜索树（BST）专题

[6.1 BST的基本操作](#6.1 BST的基本操作)

[6.2 BST与平衡二叉树（AVL）](#6.2 BST与平衡二叉树（AVL）)

七、二叉树的时间复杂度分析

总结

核心要点回顾

一、树型结构基础

1.1 树的基本概念

树是一种非线性数据结构，由n(n≥0)个节点组成的有层次关系的集合。它像一棵倒挂的树，根在上，叶在下。

树的关键特性：

  • 每个节点有零个或多个子节点

  • 没有父节点的节点称为根节点

  • 非根节点有且仅有一个父节点

  • 树中不能有环（循环引用）

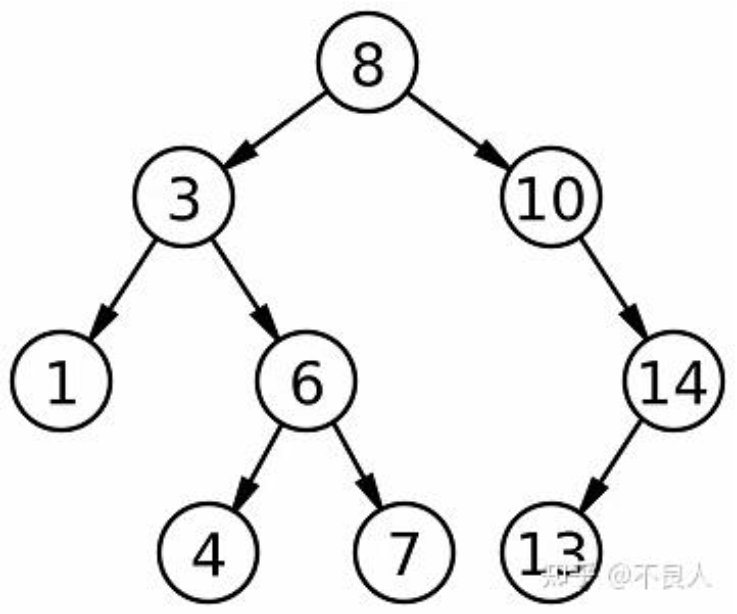
1.2 树的重要术语（面试常考）

术语 定义 示例图说明
节点的度 节点拥有的子树个数 节点A的度为3
树的度 树中所有节点的最大度 上图树的度为3
叶子节点 度为0的节点（终端节点） E、F、G、H
分支节点 度不为0的节点 A、B、C、D
父/子节点 节点的直接上下级关系 B是E的父节点，E是B的子节点
兄弟节点 同一父节点的子节点 B、C、D互为兄弟
堂兄弟节点 父节点在同一层的节点 E和G是堂兄弟
节点的层次 从根开始定义，根为第1层 A在第1层，B在第2层
树的高度 树中节点的最大层次 上图树的高度为4
祖先/子孙 路径上的所有上级/下级 A是H的祖先，H是A的子孙

1.3 树的表示方法

1.3.1 孩子兄弟表示法（最常用）
java 复制代码 
class TreeNode {
    int value;                // 节点存储的数据
    TreeNode firstChild;      // 指向第一个孩子节点
    TreeNode nextSibling;     // 指向下一个兄弟节点
    
    TreeNode(int value) {
        this.value = value;
        this.firstChild = null;
        this.nextSibling = null;
    }
}

// 示例树结构：
//        A
//       /|\
//      B C D
//     / \   \
//    E   F   G
//
// 表示方式：
// A -> B -> C -> D
// B -> E -> F
// D -> G
1.3.2 孩子表示法（每个节点存储所有孩子）
java 复制代码 
class TreeNode {
    int value;
    List<TreeNode> children;  // 存储所有子节点
    
    TreeNode(int value) {
        this.value = value;
        this.children = new ArrayList<>();
    }
}

1.4 树的应用场景

  1. 文件系统：目录和文件的层次结构

  2. 组织架构：公司的部门层级

  3. HTML/XML文档：DOM树结构

  4. 数据库索引：B树、B+树

  5. 路由算法：网络路由表

二、二叉树核心概念

2.1 二叉树的定义

二叉树是每个节点最多有两个子节点的树结构，通常称为左子节点和右子节点。

java 复制代码 
class BinaryTreeNode {
    int value;
    BinaryTreeNode left;   // 左子树
    BinaryTreeNode right;  // 右子树
    
    BinaryTreeNode(int value) {
        this.value = value;
    }
}

二叉树的特点：

  1. 节点的度 ≤ 2

  2. 左右子树有顺序，不能随意交换

  3. 即使只有一个子节点，也要区分是左还是右

2.2 特殊二叉树类型

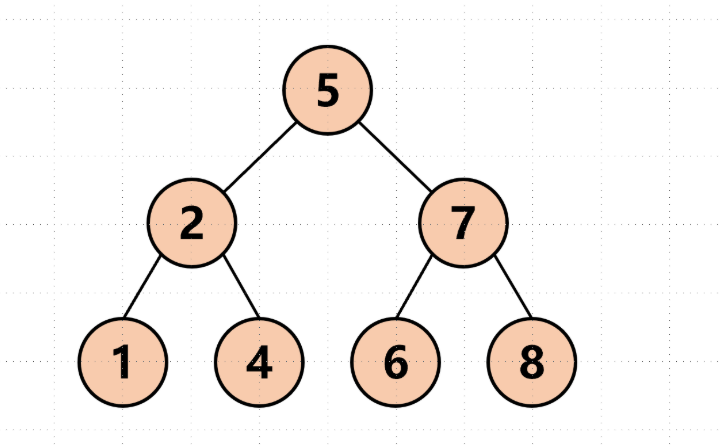
2.2.1 满二叉树 (Full Binary Tree)

  • 每一层的节点数都达到最大值

  • 深度为k的满二叉树有 2^k - 1 个节点

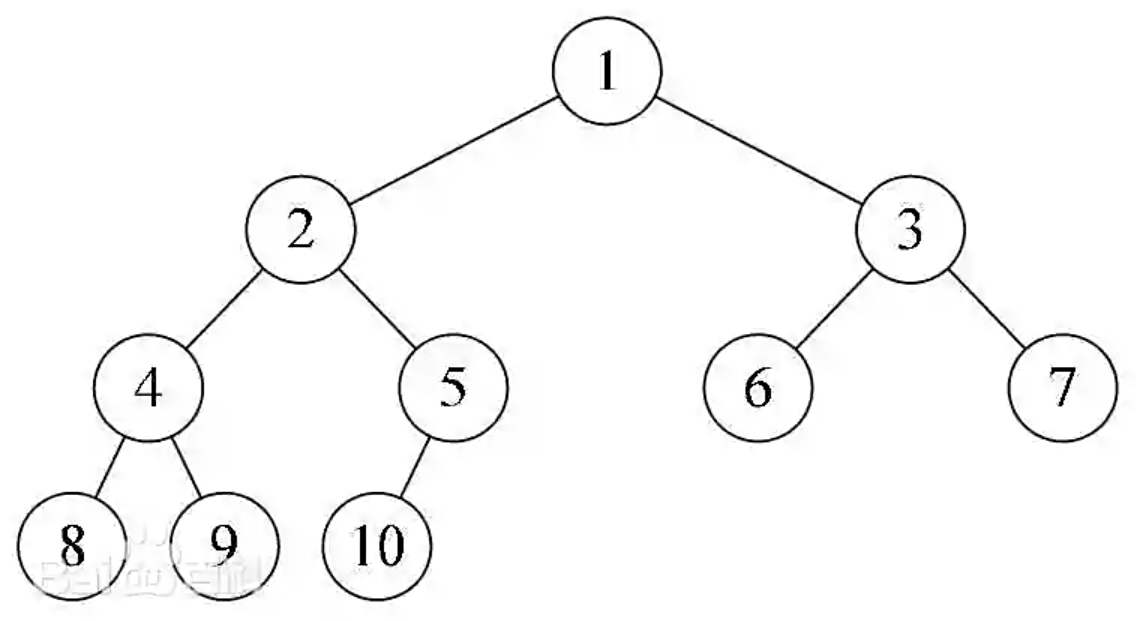
2.2.2 完全二叉树 (Complete Binary Tree)

  • 除了最后一层，其他层都是满的

  • 最后一层的节点都靠左排列

  • 堆(Heap)就是完全二叉树

2.2.3 二叉搜索树 (BST) - 重要补充
java 复制代码 
class BinarySearchTree {
    // 二叉搜索树性质：
    // 左子树上所有节点的值 < 根节点的值
    // 右子树上所有节点的值 > 根节点的值
    // 左右子树也都是二叉搜索树
}
复制代码
2.2.4 平衡二叉树 (AVL Tree) - 重要补充

  • 任意节点的左右子树高度差不超过1

  • 通过旋转操作保持平衡

2.2.5 红黑树 (Red-Black Tree) - 重要补充

  • 自平衡的二叉搜索树

  • Java的TreeMap、TreeSet底层实现

2.3 二叉树的重要性质（必背公式）

编号 性质 公式 说明
1 第i层的最大节点数 2^(i-1) i≥1
2 深度为k的二叉树最大节点数 2^k - 1 k≥1
3 叶子节点与度为2节点关系 n₀ = n₂ + 1 n₀:叶子节点，n₂:度为2的节点
4 完全二叉树的深度 ⌈log₂(n+1)⌉ n为节点数
5 完全二叉树的节点关系 父节点i，左孩子2i+1，右孩子2i+2 从0开始编号

经典例题解析：

例题1：某二叉树有399个节点，其中199个度为2的节点，求叶子节点数

根据 n₀ = n₂ + 1 = 199 + 1 = 200

答案：200

例题2：完全二叉树有767个节点，求叶子节点数

设叶子节点数为n₀，度为1的节点数为n₁，度为2的节点数为n₂

n₀ + n₁ + n₂ = 767

n₀ = n₂ + 1

完全二叉树中，n₁只能是0或1解得：n₀ = 384

2.4 二叉树的存储结构

2.4.1 链式存储（最常用）
java 复制代码 
// 二叉链表表示法
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

// 三叉链表表示法（增加父节点指针）
class TreeNodeWithParent {
    int val;
    TreeNodeWithParent left;
    TreeNodeWithParent right;
    TreeNodeWithParent parent;  // 指向父节点
}
2.4.2 顺序存储（数组表示）

  • 适合完全二叉树

  • 节点i的父节点：(i-1)/2

  • 节点i的左孩子：2i+1

  • 节点i的右孩子：2i+2

cpp 复制代码 
// 完全二叉树的数组表示
// 树结构：
//        A(0)
//       /    \
//      B(1)   C(2)
//     / \     /
//    D(3)E(4) F(5)
//
// 数组：[A, B, C, D, E, F]
// B的父节点 = (1-1)/2 = 0 (A)
// A的左孩子 = 2*0+1 = 1 (B)
// A的右孩子 = 2*0+2 = 2 (C)

三、二叉树的遍历算法

3.1 深度优先遍历 (DFS)

3.1.1 递归遍历（基础）
java 复制代码 
public class BinaryTreeTraversal {
    
    // 前序遍历：根 -> 左 -> 右
    public void preOrder(TreeNode root) {
        if (root == null) return;
        System.out.print(root.val + " ");  // 访问根节点
        preOrder(root.left);               // 遍历左子树
        preOrder(root.right);              // 遍历右子树
    }
    
    // 中序遍历：左 -> 根 -> 右
    public void inOrder(TreeNode root) {
        if (root == null) return;
        inOrder(root.left);                // 遍历左子树
        System.out.print(root.val + " ");  // 访问根节点
        inOrder(root.right);               // 遍历右子树
    }
    
    // 后序遍历：左 -> 右 -> 根
    public void postOrder(TreeNode root) {
        if (root == null) return;
        postOrder(root.left);              // 遍历左子树
        postOrder(root.right);             // 遍历右子树
        System.out.print(root.val + " ");  // 访问根节点
    }
}
3.1.2 非递归遍历（迭代，面试常考）
java 复制代码 
import java.util.Stack;

public class BinaryTreeIterativeTraversal {
    
    // 前序遍历 - 迭代法（使用栈）
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            
            // 注意：先右后左，保证出栈时是左先右后
            if (node.right != null) {
                stack.push(node.right);
            }
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        
        return result;
    }
    
    // 中序遍历 - 迭代法
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        
        while (curr != null || !stack.isEmpty()) {
            // 将左子树全部入栈
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            
            // 访问节点
            curr = stack.pop();
            result.add(curr.val);
            
            // 转向右子树
            curr = curr.right;
        }
        
        return result;
    }
    
    // 后序遍历 - 迭代法（双栈法）
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<TreeNode> stack2 = new Stack<>();
        stack1.push(root);
        
        while (!stack1.isEmpty()) {
            TreeNode node = stack1.pop();
            stack2.push(node);
            
            if (node.left != null) {
                stack1.push(node.left);
            }
            if (node.right != null) {
                stack1.push(node.right);
            }
        }
        
        while (!stack2.isEmpty()) {
            result.add(stack2.pop().val);
        }
        
        return result;
    }
}
3.1.3 莫里斯遍历 (Morris Traversal) - 空间复杂度O(1)
java 复制代码 
public class MorrisTraversal {
    // 中序遍历 - Morris算法（线索二叉树思想）
    public List<Integer> inorderMorris(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        TreeNode curr = root;
        
        while (curr != null) {
            if (curr.left == null) {
                // 如果没有左孩子，访问当前节点，转向右孩子
                result.add(curr.val);
                curr = curr.right;
            } else {
                // 找到当前节点在中序遍历下的前驱节点
                TreeNode predecessor = curr.left;
                while (predecessor.right != null && predecessor.right != curr) {
                    predecessor = predecessor.right;
                }
                
                if (predecessor.right == null) {
                    // 建立线索
                    predecessor.right = curr;
                    curr = curr.left;
                } else {
                    // 删除线索，恢复树结构
                    predecessor.right = null;
                    result.add(curr.val);
                    curr = curr.right;
                }
            }
        }
        
        return result;
    }
}

3.2 广度优先遍历 (BFS) / 层序遍历

java 复制代码 
import java.util.*;

public class LevelOrderTraversal {
    
    // 基本的层序遍历
    public List<Integer> levelOrder(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) return result;
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            result.add(node.val);
            
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        
        return result;
    }
    
    // 按层分组输出
    public List<List<Integer>> levelOrderByLevel(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root == null) return result;
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            List<Integer> levelNodes = new ArrayList<>();
            
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.poll();
                levelNodes.add(node.val);
                
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
            
            result.add(levelNodes);
        }
        
        return result;
    }
    
    // Zigzag层序遍历（蛇形遍历）
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root == null) return result;
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        boolean leftToRight = true;
        
        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            LinkedList<Integer> levelNodes = new LinkedList<>();
            
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.poll();
                
                if (leftToRight) {
                    levelNodes.addLast(node.val);
                } else {
                    levelNodes.addFirst(node.val);
                }
                
                if (node.left != null) queue.offer(node.left);
                if (node.right != null) queue.offer(node.right);
            }
            
            result.add(levelNodes);
            leftToRight = !leftToRight;
        }
        
        return result;
    }
}

3.3 遍历算法对比

遍历方式 递归复杂度 迭代复杂度 应用场景
前序遍历 时间O(n)，空间O(h) 时间O(n)，空间O(h) 复制树、序列化
中序遍历 时间O(n)，空间O(h) 时间O(n)，空间O(h) 二叉搜索树排序
后序遍历 时间O(n)，空间O(h) 时间O(n)，空间O(h) 释放树、计算高度
层序遍历 不适用 时间O(n)，空间O(w) 找最短路径、完全性判断

说明：

  • n: 节点总数

  • h: 树的高度（递归深度）

  • w: 树的最大宽度

四、二叉树基本操作实现

4.1 节点统计操作

java 复制代码 
public class BinaryTreeOperations {
    
    // 1. 计算节点总数
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        return 1 + countNodes(root.left) + countNodes(root.right);
    }
    
    // 2. 计算叶子节点数
    public int countLeafNodes(TreeNode root) {
        if (root == null) return 0;
        if (root.left == null && root.right == null) return 1;
        return countLeafNodes(root.left) + countLeafNodes(root.right);
    }
    
    // 3. 计算第k层节点数
    public int countNodesAtLevel(TreeNode root, int k) {
        if (root == null || k < 1) return 0;
        if (k == 1) return 1;
        return countNodesAtLevel(root.left, k - 1) + 
               countNodesAtLevel(root.right, k - 1);
    }
    
    // 4. 计算树的高度/深度
    public int getHeight(TreeNode root) {
        if (root == null) return 0;
        return 1 + Math.max(getHeight(root.left), getHeight(root.right));
    }
    
    // 5. 判断是否平衡二叉树
    public boolean isBalanced(TreeNode root) {
        return checkHeight(root) != -1;
    }
    
    private int checkHeight(TreeNode root) {
        if (root == null) return 0;
        
        int leftHeight = checkHeight(root.left);
        if (leftHeight == -1) return -1;
        
        int rightHeight = checkHeight(root.right);
        if (rightHeight == -1) return -1;
        
        if (Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        
        return Math.max(leftHeight, rightHeight) + 1;
    }
    
    // 6. 查找节点
    public TreeNode findNode(TreeNode root, int value) {
        if (root == null) return null;
        if (root.val == value) return root;
        
        TreeNode leftResult = findNode(root.left, value);
        if (leftResult != null) return leftResult;
        
        return findNode(root.right, value);
    }
    
    // 7. 判断两棵树是否相同
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) return true;
        if (p == null || q == null) return false;
        if (p.val != q.val) return false;
        
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }
    
    // 8. 判断是否对称二叉树
    public boolean isSymmetric(TreeNode root) {
        if (root == null) return true;
        return isMirror(root.left, root.right);
    }
    
    private boolean isMirror(TreeNode t1, TreeNode t2) {
        if (t1 == null && t2 == null) return true;
        if (t1 == null || t2 == null) return false;
        if (t1.val != t2.val) return false;
        
        return isMirror(t1.left, t2.right) && isMirror(t1.right, t2.left);
    }
}

4.2 树的结构操作

java 复制代码 
public class BinaryTreeStructureOperations {
    
    // 1. 反转/镜像二叉树
    public TreeNode invertTree(TreeNode root) {
        if (root == null) return null;
        
        // 交换左右子树
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        
        // 递归反转左右子树
        invertTree(root.left);
        invertTree(root.right);
        
        return root;
    }
    
    // 2. 构建二叉树（根据前序和中序）
    public TreeNode buildTreeFromPreIn(int[] preorder, int[] inorder) {
        Map<Integer, Integer> inorderMap = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            inorderMap.put(inorder[i], i);
        }
        return buildTreePreInHelper(preorder, 0, preorder.length - 1,
                                    inorder, 0, inorder.length - 1, inorderMap);
    }
    
    private TreeNode buildTreePreInHelper(int[] preorder, int preStart, int preEnd,
                                         int[] inorder, int inStart, int inEnd,
                                         Map<Integer, Integer> inorderMap) {
        if (preStart > preEnd || inStart > inEnd) return null;
        
        TreeNode root = new TreeNode(preorder[preStart]);
        int inorderRootIndex = inorderMap.get(root.val);
        int leftSubtreeSize = inorderRootIndex - inStart;
        
        root.left = buildTreePreInHelper(preorder, preStart + 1, preStart + leftSubtreeSize,
                                        inorder, inStart, inorderRootIndex - 1, inorderMap);
        root.right = buildTreePreInHelper(preorder, preStart + leftSubtreeSize + 1, preEnd,
                                         inorder, inorderRootIndex + 1, inEnd, inorderMap);
        
        return root;
    }
    
    // 3. 寻找最近公共祖先 (LCA)
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) return root;
        
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        
        if (left != null && right != null) return root;  // p和q在左右子树
        return left != null ? left : right;  // p和q在同一侧子树
    }
    
    // 4. 判断完全二叉树
    public boolean isCompleteTree(TreeNode root) {
        if (root == null) return true;
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        boolean end = false;
        
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            
            if (node == null) {
                end = true;
            } else {
                if (end) return false;  // 遇到空节点后又遇到非空节点
                queue.offer(node.left);
                queue.offer(node.right);
            }
        }
        
        return true;
    }
    
    // 5. 序列化和反序列化二叉树
    public String serialize(TreeNode root) {
        if (root == null) return "#";
        return root.val + "," + serialize(root.left) + "," + serialize(root.right);
    }
    
    public TreeNode deserialize(String data) {
        Queue<String> queue = new LinkedList<>(Arrays.asList(data.split(",")));
        return deserializeHelper(queue);
    }
    
    private TreeNode deserializeHelper(Queue<String> queue) {
        String val = queue.poll();
        if (val.equals("#")) return null;
        
        TreeNode root = new TreeNode(Integer.parseInt(val));
        root.left = deserializeHelper(queue);
        root.right = deserializeHelper(queue);
        
        return root;
    }
}

五、二叉树常见面试题深度解析

5.1 最近公共祖先（LCA）问题扩展

java 复制代码 
public class LCASolutions {
    
    // 方法1：递归（通用二叉树）
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) return root;
        
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        
        if (left != null && right != null) return root;
        return left != null ? left : right;
    }
    
    // 方法2：存储父节点（通用二叉树）
    public TreeNode lowestCommonAncestorWithParent(TreeNode root, TreeNode p, TreeNode q) {
        Map<TreeNode, TreeNode> parent = new HashMap<>();
        Set<TreeNode> ancestors = new HashSet<>();
        
        // 记录每个节点的父节点
        recordParents(root, parent);
        
        // 记录p的所有祖先
        while (p != null) {
            ancestors.add(p);
            p = parent.get(p);
        }
        
        // 找到q的第一个在p祖先集合中的祖先
        while (q != null) {
            if (ancestors.contains(q)) return q;
            q = parent.get(q);
        }
        
        return null;
    }
    
    private void recordParents(TreeNode root, Map<TreeNode, TreeNode> parent) {
        if (root.left != null) {
            parent.put(root.left, root);
            recordParents(root.left, parent);
        }
        if (root.right != null) {
            parent.put(root.right, root);
            recordParents(root.right, parent);
        }
    }
    
    // 方法3：二叉搜索树的LCA（利用BST性质）
    public TreeNode lowestCommonAncestorBST(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val > p.val && root.val > q.val) {
            return lowestCommonAncestorBST(root.left, p, q);
        } else if (root.val < p.val && root.val < q.val) {
            return lowestCommonAncestorBST(root.right, p, q);
        } else {
            return root;  // p和q在root两侧
        }
    }
}

5.2 二叉树的直径问题

java 复制代码 
public class TreeDiameter {
    private int maxDiameter = 0;
    
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return maxDiameter;
    }
    
    private int maxDepth(TreeNode root) {
        if (root == null) return 0;
        
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        
        // 更新最大直径：左子树深度 + 右子树深度
        maxDiameter = Math.max(maxDiameter, leftDepth + rightDepth);
        
        // 返回当前节点的深度
        return Math.max(leftDepth, rightDepth) + 1;
    }
}

5.3 二叉树的最大路径和

java 复制代码 
public class MaxPathSum {
    private int maxSum = Integer.MIN_VALUE;
    
    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }
    
    private int maxGain(TreeNode node) {
        if (node == null) return 0;
        
        // 递归计算左右子树的最大贡献值
        // 只有贡献值大于0时才选择该路径
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);
        
        // 当前节点的最大路径和
        int priceNewpath = node.val + leftGain + rightGain;
        
        // 更新全局最大值
        maxSum = Math.max(maxSum, priceNewpath);
        
        // 返回节点的最大贡献值
        return node.val + Math.max(leftGain, rightGain);
    }
}

六、二叉搜索树（BST）专题

6.1 BST的基本操作

java 复制代码 
public class BinarySearchTree {
    TreeNode root;
    
    // 1. 查找节点
    public TreeNode search(int key) {
        TreeNode current = root;
        while (current != null) {
            if (key == current.val) {
                return current;
            } else if (key < current.val) {
                current = current.left;
            } else {
                current = current.right;
            }
        }
        return null;
    }
    
    // 2. 插入节点
    public void insert(int key) {
        root = insertRecursive(root, key);
    }
    
    private TreeNode insertRecursive(TreeNode root, int key) {
        if (root == null) {
            return new TreeNode(key);
        }
        
        if (key < root.val) {
            root.left = insertRecursive(root.left, key);
        } else if (key > root.val) {
            root.right = insertRecursive(root.right, key);
        }
        
        return root;
    }
    
    // 3. 删除节点（三种情况）
    public void delete(int key) {
        root = deleteRecursive(root, key);
    }
    
    private TreeNode deleteRecursive(TreeNode root, int key) {
        if (root == null) return null;
        
        if (key < root.val) {
            root.left = deleteRecursive(root.left, key);
        } else if (key > root.val) {
            root.right = deleteRecursive(root.right, key);
        } else {
            // 找到要删除的节点
            // 情况1：叶子节点
            if (root.left == null && root.right == null) {
                return null;
            }
            // 情况2：只有一个子节点
            else if (root.left == null) {
                return root.right;
            } else if (root.right == null) {
                return root.left;
            }
            // 情况3：有两个子节点
            else {
                // 找到右子树的最小节点（或左子树的最大节点）
                TreeNode minNode = findMin(root.right);
                root.val = minNode.val;
                root.right = deleteRecursive(root.right, minNode.val);
            }
        }
        
        return root;
    }
    
    private TreeNode findMin(TreeNode node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }
    
    // 4. 验证BST
    public boolean isValidBST(TreeNode root) {
        return validate(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    
    private boolean validate(TreeNode node, long min, long max) {
        if (node == null) return true;
        if (node.val <= min || node.val >= max) return false;
        
        return validate(node.left, min, node.val) && 
               validate(node.right, node.val, max);
    }
    
    // 5. BST的中序遍历（得到有序序列）
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorderHelper(root, result);
        return result;
    }
    
    private void inorderHelper(TreeNode root, List<Integer> result) {
        if (root == null) return;
        inorderHelper(root.left, result);
        result.add(root.val);
        inorderHelper(root.right, result);
    }
}

6.2 BST与平衡二叉树（AVL）

java 复制代码 
public class AVLTree {
    class AVLNode {
        int val, height;
        AVLNode left, right;
        
        AVLNode(int val) {
            this.val = val;
            this.height = 1;
        }
    }
    
    private AVLNode root;
    
    // 获取节点高度
    private int height(AVLNode node) {
        return node == null ? 0 : node.height;
    }
    
    // 获取平衡因子
    private int getBalance(AVLNode node) {
        return node == null ? 0 : height(node.left) - height(node.right);
    }
    
    // 右旋转
    private AVLNode rightRotate(AVLNode y) {
        AVLNode x = y.left;
        AVLNode T2 = x.right;
        
        x.right = y;
        y.left = T2;
        
        y.height = Math.max(height(y.left), height(y.right)) + 1;
        x.height = Math.max(height(x.left), height(x.right)) + 1;
        
        return x;
    }
    
    // 左旋转
    private AVLNode leftRotate(AVLNode x) {
        AVLNode y = x.right;
        AVLNode T2 = y.left;
        
        y.left = x;
        x.right = T2;
        
        x.height = Math.max(height(x.left), height(x.right)) + 1;
        y.height = Math.max(height(y.left), height(y.right)) + 1;
        
        return y;
    }
    
    // 插入节点并平衡
    public void insert(int key) {
        root = insertRecursive(root, key);
    }
    
    private AVLNode insertRecursive(AVLNode node, int key) {
        if (node == null) return new AVLNode(key);
        
        if (key < node.val) {
            node.left = insertRecursive(node.left, key);
        } else if (key > node.val) {
            node.right = insertRecursive(node.right, key);
        } else {
            return node;  // 不允许重复值
        }
        
        // 更新高度
        node.height = 1 + Math.max(height(node.left), height(node.right));
        
        // 获取平衡因子
        int balance = getBalance(node);
        
        // 平衡维护（四种情况）
        // 左左情况
        if (balance > 1 && key < node.left.val) {
            return rightRotate(node);
        }
        
        // 右右情况
        if (balance < -1 && key > node.right.val) {
            return leftRotate(node);
        }
        
        // 左右情况
        if (balance > 1 && key > node.left.val) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        
        // 右左情况
        if (balance < -1 && key < node.right.val) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        
        return node;
    }
}

七、二叉树的时间复杂度分析

操作 普通二叉树 平衡二叉树 (AVL/红黑树) 二叉搜索树 (最坏)
查找 O(n) O(log n) O(n)
插入 O(1) O(log n) O(n)
删除 O(1) O(log n) O(n)
遍历 O(n) O(n) O(n)
最小/最大 O(n) O(log n) O(n)
前驱/后继 O(n) O(log n) O(n)

空间复杂度：

  • 递归遍历：O(h)，h为树的高度

  • 迭代遍历：O(n)最坏情况

  • 存储结构：O(n)

总结

二叉树是数据结构中最重要、最基础的非线性结构，掌握二叉树对于学习更复杂的数据结构（如堆、图、Trie树等）至关重要。

核心要点回顾：

  1. 基本概念：理解二叉树定义、特性、分类

  2. 遍历算法：掌握四种遍历方式（前中后层）的递归和迭代实现

  3. 操作实现：熟练实现各种基本操作（查找、插入、删除、判断等）

  4. 应用场景：理解二叉树在算法和系统中的应用

  5. 时间复杂度：分析不同操作的效率

相关推荐
冷冷的菜哥1 小时前
springboot调用ffmpeg实现对视频的截图，截取与水印
java·spring boot·ffmpeg·音视频·水印·截图·截取
2501_940315262 小时前
蓝桥云课：分巧克力（二分查找法）
数据结构·c++·算法
csuzhucong2 小时前
2种闪蝶魔方（待更新）
算法
VT.馒头2 小时前
【力扣】2637. 有时间限制的 Promise 对象
前端·javascript·leetcode·typescript
C++chaofan2 小时前
JUC并发编程：LockSupport.park() 与 unpark() 深度解析
java·开发语言·c++·性能优化·高并发·juc
人工智能AI技术2 小时前
Java程序员如何入门AI
java·人工智能
我是小疯子662 小时前
C++图论：从基础到实战应用
java·c++·图论
小码过河.2 小时前
设计模式——享元模式
java·设计模式·享元模式
J_liaty2 小时前
深入理解Java反射：原理、应用与最佳实践
java·开发语言·反射
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）032025年大语言模型技术全景报告04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Claude Code Skills 实用使用手册07UV安装并设置国内源08Labelme从安装到标注：零基础完整指南09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10BongoCat - 跨平台键盘猫动画工具