LeetCode 3047.求交集区域内的最大正方形面积：2层循环暴力枚举

【LetMeFly】3047.求交集区域内的最大正方形面积：2层循环暴力枚举

力扣题目链接：https://leetcode.cn/problems/find-the-largest-area-of-square-inside-two-rectangles/

在二维平面上存在 n 个矩形。给你两个下标从 0 开始的二维整数数组 bottomLeft 和 topRight，两个数组的大小都是 n x 2 ，其中 bottomLeft[i] 和 topRight[i] 分别代表第 i 个矩形的左下角 和 右上角坐标。

我们定义向右的方向为 x 轴正半轴（x 坐标增加 ），向左的方向为 x 轴负半轴（x 坐标减少 ）。同样地，定义向上的方向为 y 轴正半轴（y 坐标增加 ），向下 的方向为 y 轴负半轴（y 坐标减少）。

你可以选择一个区域，该区域由两个矩形的交集形成。你需要找出能够放入该区域内的最大正方形面积，并选择最优解。

返回能够放入交集区域的正方形的最大可能面积，如果矩形之间不存在任何交集区域，则返回 0。

示例 1：

复制代码

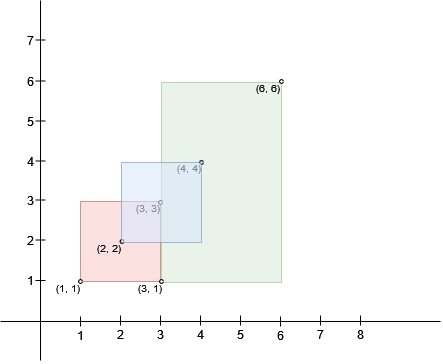
输入：bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
输出：1
解释：边长为 1 的正方形可以放入矩形 0 和矩形 1 的交集区域，或矩形 1 和矩形 2 的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。
可以证明，边长更大的正方形无法放入任何交集区域。

示例 2：

复制代码

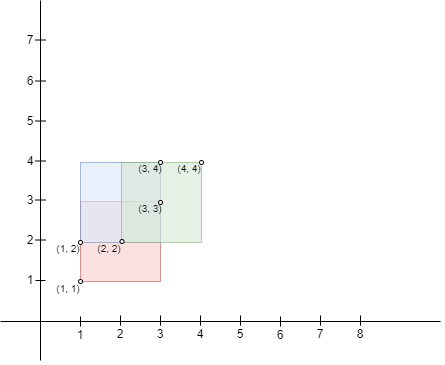
输入：bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
输出：1
解释：边长为 1 的正方形可以放入矩形 0 和矩形 1，矩形 1 和矩形 2，或所有三个矩形的交集区域。因此最大面积是边长 * 边长，即 1 * 1 = 1。
可以证明，边长更大的正方形无法放入任何交集区域。
请注意，区域可以由多于两个矩形的交集构成。

示例 3：

复制代码

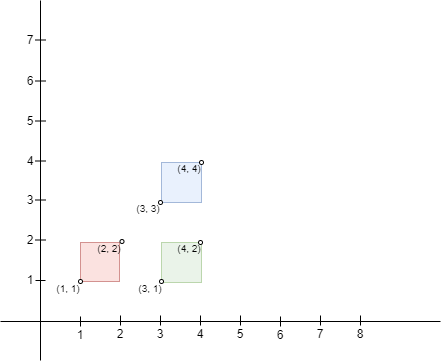
输入：bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
输出：0
解释：不存在相交的矩形，因此，返回 0 。

提示：

n == bottomLeft.length == topRight.length
2 <= n <= 10³
bottomLeft[i].length == topRight[i].length == 2
1 <= bottomLeft[i][0], bottomLeft[i][1] <= 10⁷
1 <= topRight[i][0], topRight[i][1] <= 10⁷
bottomLeft[i][0] < topRight[i][0]
bottomLeft[i][1] < topRight[i][1]

解题方法：暴力模拟

一维坐标上，一个线段坐标从 a a a到 b b b，一个线段坐标从 c c c到 d d d，它们的相交部分有多长？

min ⁡ ( b , d ) − max ⁡ ( a , c ) \min(b, d) - \max(a, c) min(b,d)−max(a,c)，再与 0 0 0取一个最大值就好了（右端点最小值减去左端点最大值）

依次判断两个正方形在横纵坐标轴上的相交长度，最小值的平方即为最大正方形的面积。

时间复杂度 O ( n 2 ) O(n^2) O(n2)
空间复杂度 O ( 1 ) O(1) O(1)

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2026-01-17 20:02:05
 */
typedef long long ll;

class Solution {
private:
    // a->b VS c->d
    ll getDiff(int a, int b, int c, int d) {
        return max(0, min(b, d) - max(a, c));
    }
public:
    long long largestSquareArea(vector<vector<int>>& bottomLeft, vector<vector<int>>& topRight) {
        ll ans = 0;
        for (int i = 0; i < bottomLeft.size(); i++) {
            for (int j = i + 1; j < bottomLeft.size(); j++) {
                ll dx = getDiff(bottomLeft[i][0], topRight[i][0], bottomLeft[j][0], topRight[j][0]);
                ll dy = getDiff(bottomLeft[i][1], topRight[i][1], bottomLeft[j][1], topRight[j][1]);
                ans = max(ans, min(dx, dy) * min(dx, dy));
            }
        }
        return ans;
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源