1.(1863.)找出所有子集的异或总和再求和

与之前写过的题类似,首先求所有子集,再在过程中计算异或和。还是设置全局变量,之前的path是用来保存路径的,本题用于保存当前层路径的异或和,没有递归出口通过循环来控制下标,通过可选位置来判断是否为有效子集可以避免无效遍历,参数传递需要一个参数来标记当前递归到哪一层了,每次递归将path值加入到全局变量num中保存和,回溯的恢复现场通过异或两个相同的数相互抵消的性质来进行
cpp
class Solution {
int path;
int num;//计算异或和的结果
public:
void dfs(vector<int>& nums,int pos)
{
num+=path;
int n=0;//0异或任何数都等于它本身
for(int i=pos;i<nums.size();i++)
{
path^=nums[i];
dfs(nums,i+1);//注意这里传入的参数为i,pos是不会变化的
path^=nums[i];//回溯->恢复现场
}
}
int subsetXORSum(vector<int>& nums) {
dfs(nums,0);
return num;
}
};2. (47.) 全排列 II

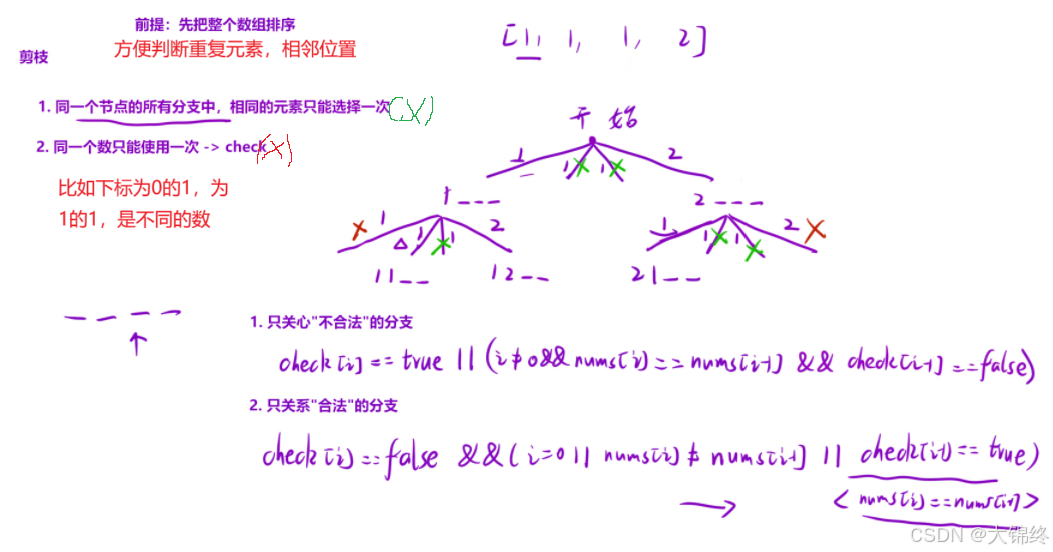
- 关心不合法分支的解释:
这个条件是判断当前分支是否 "非法"(需要剪枝),满足该条件的分支会被跳过
check[i] == true:check 是标记数组(记录元素是否已被使用),true 表示当前元素已被选过 → 非法(违反 "同一个数只能用一次");
(i != 0 && nums[i] == nums[i-1] && check[i-1] == false):
i != 0:避免数组越界;
nums[i] == nums[i-1]:当前元素和前一个元素值相同;
check[i-1] == false:前一个元素未被使用(说明是 "同一层递归" 中重复的元素)→ 非法(违反 "同一节点分支中相同元素只能选一次")。
- 关心合法分支的解释:
这个条件是判断当前分支是否 "合法"(可以继续递归),满足该条件的分支会被保留
check[i] == false:当前元素未被使用(满足 "同一个数只能用一次");
同时满足以下任一子条件(保证 "同一节点分支中相同元素只选一次"):
i == 0:当前是数组第一个元素,无前置元素,直接合法;
nums[i] != nums[i-1]:当前元素和前一个元素值不同,直接合法;
check[i-1] == true:前一个元素已被使用(说明是 "不同层递归" 中选的重复元素,不违反约束)。
- 关于两种分支的判断代码中任选一种即可
cpp
class Solution {
vector<vector<int>>ret;
bool check[8];
vector<int> path;
public:
void dfs(vector<int>&nums)//path回溯时恢复现场的工作由函数自己实现了
{
//递归出口
if(path.size()==nums.size())
{
ret.push_back(path);
return;
}
for(int i=0;i<nums.size();i++)//遍历每一种可能的情况
{
if(!check[i])
{
//递归调用
if(check[i]==1||(i!=0&&nums[i]==nums[i-1])&&check[i-1]==0) continue;
path.push_back(nums[i]);
check[i]=1;
dfs(nums);
check[i]=0;
path.pop_back();
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(),nums.end());
dfs(nums);
return ret;
}
};3. (17.) 电话号码的字母组合

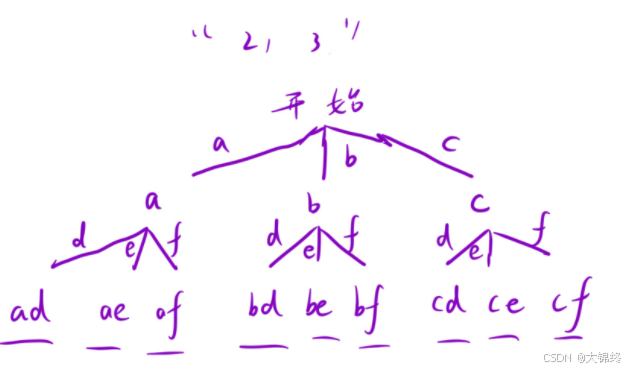
用一个字符数组来记录每个数字所对应的字符串,用哈希表也行,画出决策树后就可以开始分析递归回溯过程了,与之前思路相同,用一个全局变量来记录结果,一个全局变量来记录生成的结果,每一层都要对传入的字符串每一个字符可能形成的结果进行深搜,返回时要恢复现场
cpp
class Solution {
string strr[10]={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> ret;
string path;
public:
void dfs(string &digits,int pos)
{
if(pos==digits.size()){
ret.push_back(path);
return ;
}
for(char a:strr[digits[pos]-'0'])
{
path+=a;
dfs(digits,pos+1);
path.pop_back();
}
}
vector<string> letterCombinations(string digits) {
if(digits=="") return ret;
dfs(digits,0);
return ret;
}
};4. (22.) 括号生成
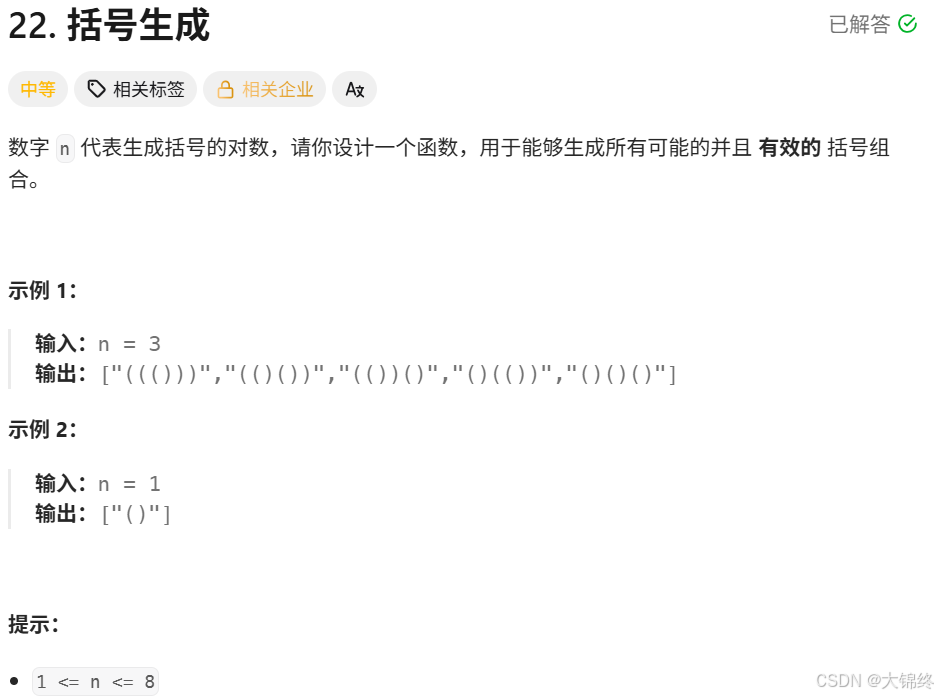
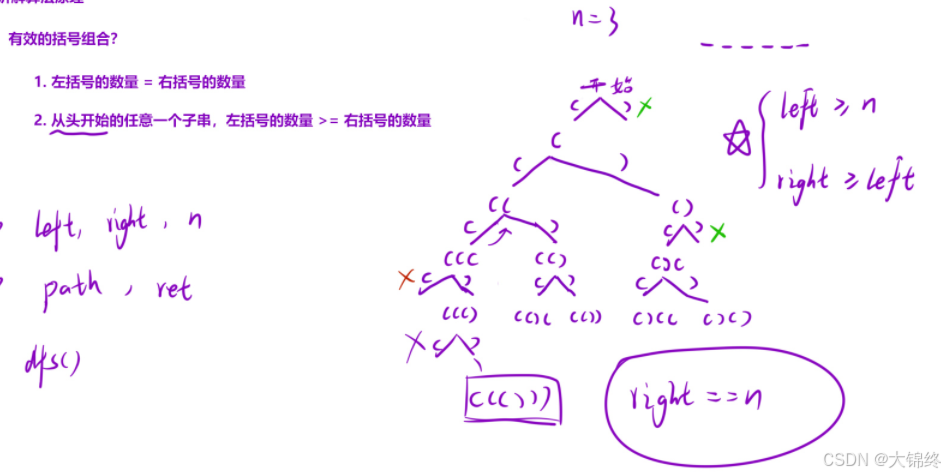
首先明确有效括号的条件,几对括号可以转化为对应有多少个位置可以填括号,以此深搜,进行剪枝优化结果。用left、right记录当前左右括号数量,n为括号对数,path为当前组合,ret为最终结果,都设置为全局变量时dfs就无参,调用很方便,注意回溯后的手动恢复现场
cpp
class Solution {
int len;
int left;
int right;
vector<string> ret;
string path;
public:
vector<string> generateParenthesis(int n) {
len = n;
dfs();
return ret;
}
void dfs() {
if (right == len) {
ret.push_back(path);
return;
}
if (left < len) {//独立判断分支,(不行就加),不要固定死先左后右,
path += '(';
left++;
dfs();
path.pop_back();
left--;
}
if (right < left) {
path += ')';
right++;
dfs();
path.pop_back(); // 恢复现场
right--;
}
}
};- 参数临时变量写法:
cpp
class Solution {
int len;
vector<string> ret;
public:
vector<string> generateParenthesis(int n) {
len = n;
int left=0,right=0;
string path;
dfs(left,right,path);
return ret;
}
void dfs(int left,int right,string path) {
if (right == len) {
ret.push_back(path);
return;
}
if (left < len) {//独立判断分支,(不行就加),不要固定死先左后右,
dfs(left+1,right,path+'(');//值传递时,不要修改原始参数,直接传递临时修改后的值,否则会状态污染,导致下一个执行流重复使用
}
if (right < left) {
dfs(left,right+1,path+')');
}
}
};值传递的核心优势是「天然回溯」------ 因为下一层递归接收的是 "临时修改后的值",而当前层的参数副本始终是原始值,递归返回后无需做任何手动恢复(比如path.pop_back()、left--),直接执行下一个分支即可。
简单记:
错误做法:修改值传递的副本 → 同一层分支共用修改后的状态 → 状态污染;
正确做法:不修改副本,直接传递临时修改后的值 → 同一层分支状态独立 → 天然回溯。
5. (77.) 组合

算法思路:
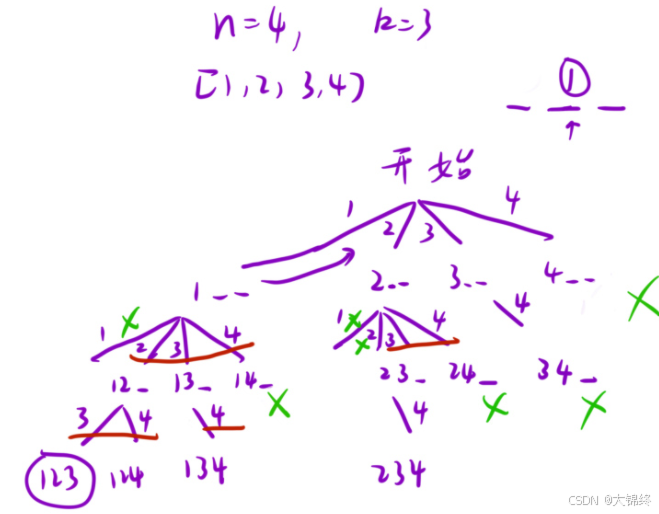
题目要求我们从 1 到 n 中选择 k 个数的所有组合,其中不考虑顺序。也就是说,[1,2] 和 [2,1] 等价。我们需要找出所有的组合,但不能重复计算相同元素的不同顺序的组合。对于选择组合,我们需要进行如下流程:
- 所有元素分别作为首位元素进行处理;
- 在之后的位置上同理,选择所有元素分别作为当前位置元素进行处理;
- 为避免计算重复组合,规定选择之后位置的元素时必须比前⼀个元素大,这样就不会有重复的组合([1,2] 和 [2,1] 中 [2,1] 不会出现)。相当于剪枝操作
cpp
class Solution {
vector<vector<int>>ret;
vector<int>path;
int len;
public:
vector<vector<int>> combine(int n, int k) {
len=k;
dfs(n,1);
return ret;
}
void dfs(int n,int pos)
{
if(path.size()==len){
ret.push_back(path);
return;
}
for(int i=pos;i<=n;i++)
{
path.push_back(i);
dfs(n,i+1);
path.pop_back();//恢复现场
}
}
};6. (494.) 目标和

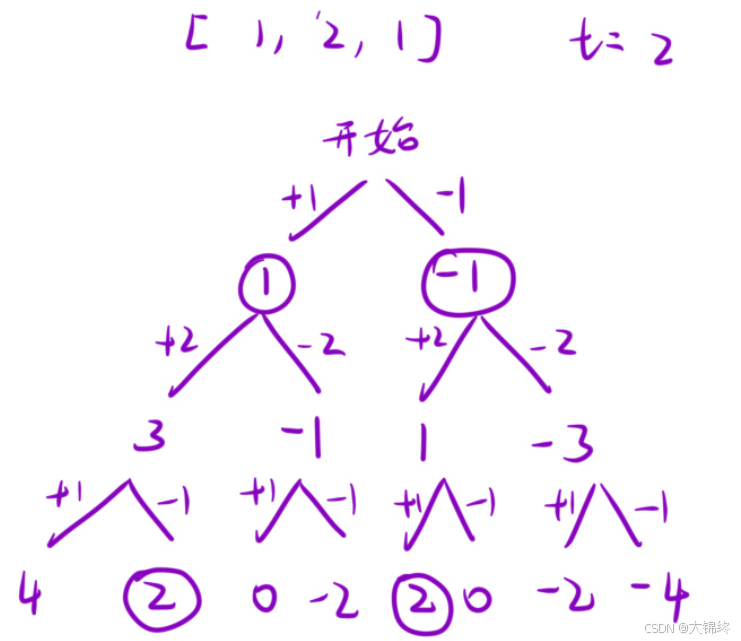
将搜索树画出来后就有思路了,每个位置只有两种选择,+或-,当遍历完所有元素后再判断是否等于目标和。
注意:
这里不能用for循环来控制递归深度,for循环适用排列、组合和子集的场景,递归分支数不确定和递归深度不固定的场景,而本题每个元素必须处理且只有固定选择,递归分支数与深度都固定
- 全局变量形式:
cpp
class Solution {
int ret;
int path;
public:
int findTargetSumWays(vector<int>& nums, int target) {
dfs(nums,target,0);
return ret;
}
void dfs(vector<int>& nums, int target,int pos)
{
if(pos==nums.size())
{
if(path==target)
{
ret+=1;
}
return ;
}
path+=nums[pos];
dfs(nums,target,pos+1);
//恢复现场
path-=nums[pos];
path-=nums[pos];
dfs(nums,target,pos+1);
path+=nums[pos];
}
};- 临时变量传参:
cpp
class Solution {
int ret;
int path;
public:
int findTargetSumWays(vector<int>& nums, int target) {
dfs(nums,target,0,path);
return ret;
}
void dfs(vector<int>& nums, int target,int pos,int path)
{
if(pos==nums.size())
{
if(path==target) ret+=1;
return ;
}
dfs(nums,target,pos+1,path+nums[pos]);
dfs(nums,target,pos+1,path-nums[pos]);
}
};由堆栈自动销毁当前层的临时变量来恢复现场
7. (39.) 组合总和

- 解法1:
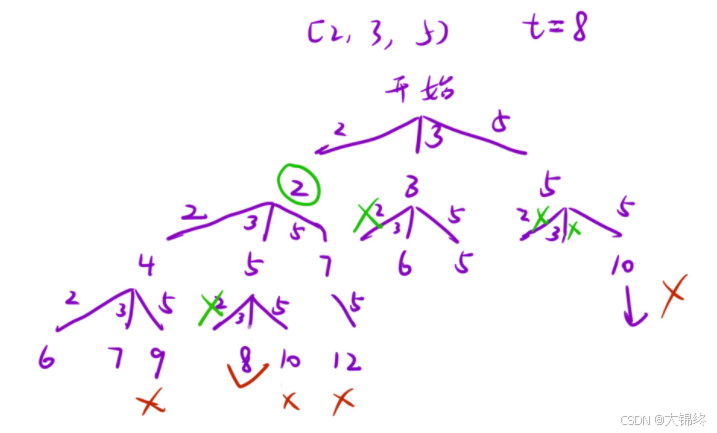
给定数组大小上,对每个位置可以填什么进行判断,由于不计顺序并且元素可以重复选择,所以要对重复组合进行剪枝操作,dfs中传入的pos就决定了下一轮遍历不会选到重复顺序的元素
cpp
class Solution {
vector<vector<int>> ret;
vector<int> path;
int n;
public:
vector<vector<int>> combinationSum(vector<int>& c, int t) {
dfs(c, t,0);
return ret;
}
void dfs(vector<int>& c, int t,int pos)
{
if(n==t)
{
ret.push_back(path);
return;
}
if(n>t||pos==c.size()) return;
for(int i=pos;i<c.size();i++)
{
path.push_back(c[i]);
n+=c[i];
dfs(c,t,i);
path.pop_back();
n-=c[i];
}
}
};- 解法2:
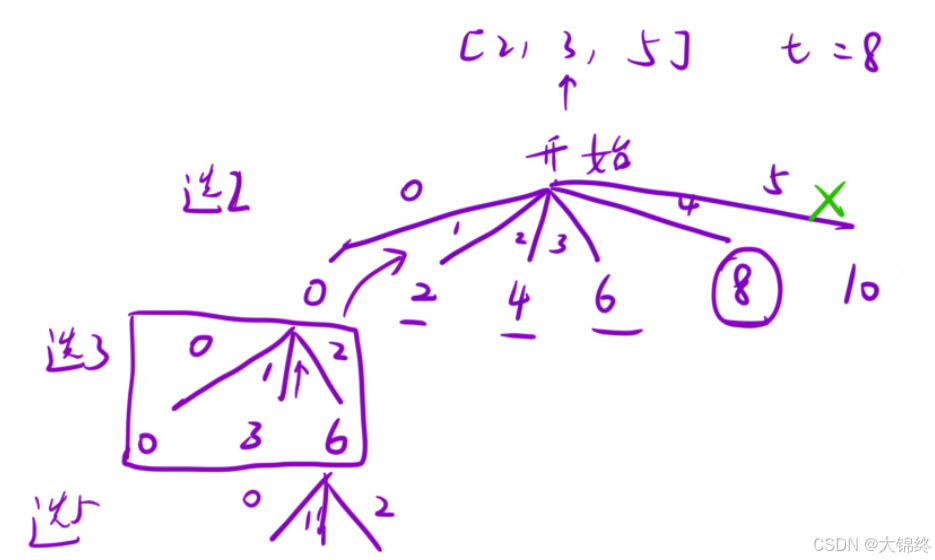
对每个元素可使用多少个来依次进行判断,直到累加和超过目标值开始计算下一个元素最可使用多少个,注意恢复现场时要在上一个元素被使用固定次数的基础上遍历完一个元素所有可能使用的次数之后,不然要重复添加元素到path中,例如上图中0元素下选3的方框部分全部完成后再进行现场恢复
cpp
class Solution {
vector<vector<int>> ret;
vector<int> path;
public:
vector<vector<int>> combinationSum(vector<int>& c, int t) {
int n=0;
dfs(c, t,0,n);
return ret;
}
void dfs(vector<int>& c, int t,int pos,int n)
{
if(n==t){
ret.push_back(path);
return ;
}
if(pos==c.size()||n>t) return;
//枚举个数
for(int i=0;i*c[pos]+n<=t;i++)
{
if(i) path.push_back(c[pos]);
dfs(c,t,pos+1,n+i*c[pos]);
}
//恢复现场
for(int i=1;i*c[pos]+n<=t;i++)
{
path.pop_back();//恢复现场
}
}
};8. (784.) 字母大小写全排列

由于只需要对英文字母的大小写进行处理,所以属于固定分支情况,每次只用考虑大小写改变或不改变两种情况,用pos下标控制遍历长度即可,不能使用for循环
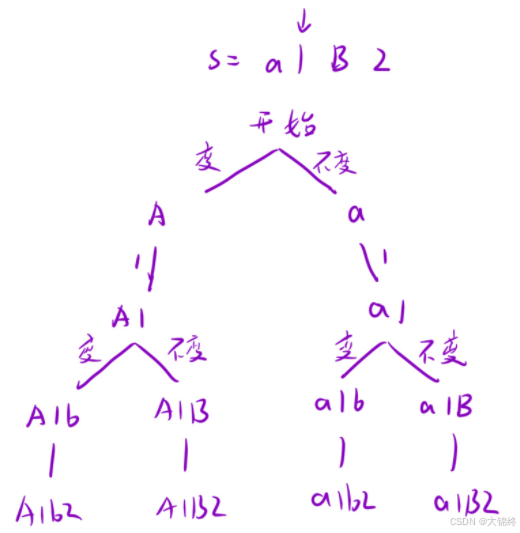
cpp
class Solution {
vector<string> ret;
public:
vector<string> letterCasePermutation(string s) {
string path;
dfs(s,path,0);
return ret;
}
void dfs(string s,string path,int pos)
{
if(pos==s.size()){
ret.push_back(path);
return ;
}
//不改变(字符为数字时逻辑同样适用)
dfs(s,path+s[pos],pos+1);
//改变
if(s[pos]>'9'||s[pos]<'0') {
dfs(s,path+change(s[pos]),pos+1);
}
}
char change(char s)//处理大小写转换
{
if(s>='a'&&s<='z') s-=32;
else s+=32;
return s;
}
};9. (526.) 优美的排列

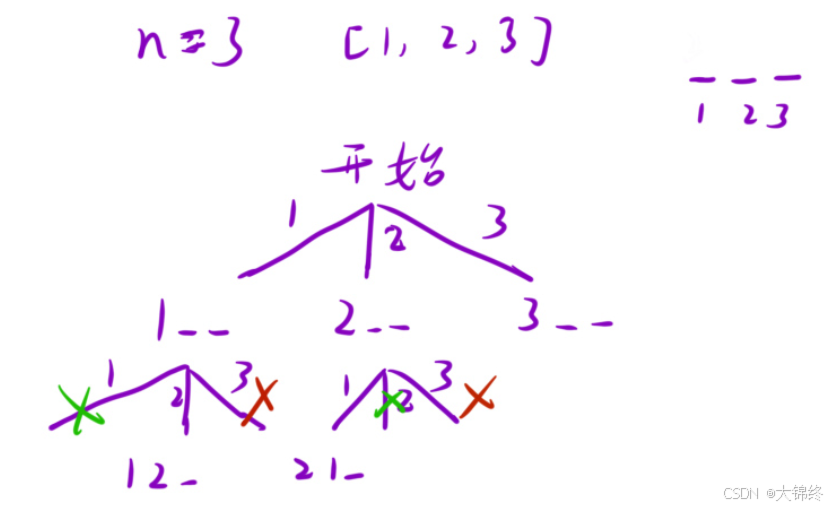
思路:
在每⼀个位置上考虑所有的可能情况并且不能出现重复。通过深度优先搜索的⽅式,不断地枚举每个数在当前位置的可能性,并回溯到上⼀个状态,直到枚举完所有可能性,得到正确的结果。我们需要定义⼀个变量 ⽤来记录所有可能的排列数量,⼀个⼀维数组 visited 标记元素,然后从第⼀个位置开始进⾏递归;
递归流程:
- 递归结束条件:当 index 等于 n 时,说明已经处理完了所有数字,将当前数组存⼊结果中;
- 在每个递归状态中,枚举所有下标 x,若这个下标未被标记,并且满⾜题⽬条件之⼀:
a. 将 check[x] 标记为 1;
b. 对第 index+1 个位置进⾏递归;
c. 将 check[x] 重新赋值为 0,表⽰回溯;
cpp
class Solution {
int ret;
vector<bool> check;
public:
int countArrangement(int n) {
check.resize(n+1,false);
dfs(n,1);
return ret;
}
void dfs(int n,int pos)
{
if(pos==n+1)
{
ret++;
return;
}
//递归
for(int i=1;i<=n;i++)//i代表每个数,pos代表下标位置
{
if(check[i]==false&&(i%pos==0||pos%i==0))
{
check[i]=true;
dfs(n,pos+1);
check[i]=false;//恢复现场
}
}
}
};10. (51.) N 皇后

决策树长这样,以每一行哪个位置可以放皇后去依次遍历,关键在于如何剪枝
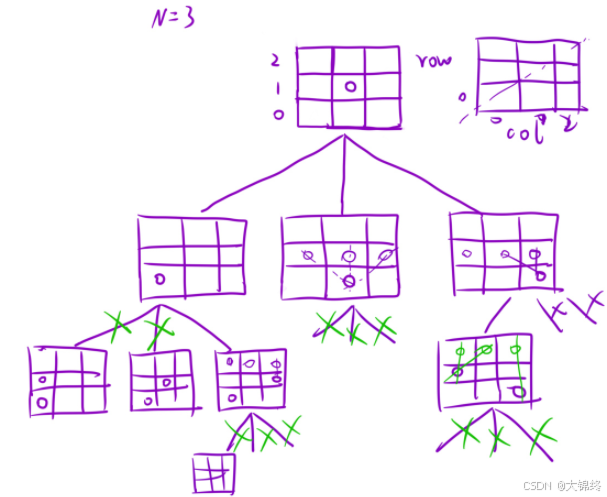
- 剪枝操作:
由题意得需要判断行、列、两个对角线上是否有皇后,由于决策树是通过行来画的,所以天然不会重复,只需考虑另外三个
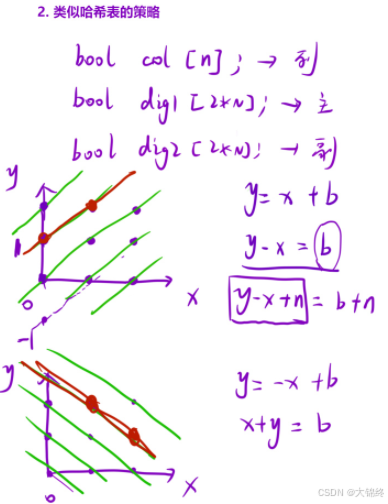
关于列:以一行中每个位置作为列的下标,bool数组判断是否有皇后放置
两个对角线:放到直角坐标系中,每两个点之间的坐标差值相同,又根据左右对角线在坐标系中不同的斜率,由两个不等式来计算数组中下标的对应位置是否有皇后放置,注意其中一个下标计算可能为负数,整体加上n即可
注意:
path存储的是整个棋盘中皇后的位置,可以先初始化所有位置为'.',再判断皇后位置来改变,每一行皇后位置可以创建string来记录加入到path中,递归出口满足时path加入到ret中,回溯时path记得恢复现场
cpp
class Solution {
vector<vector<string>> ret;
vector<string> path;
bool col[10];
bool dig1[20];
bool dig2[20];
public:
vector<vector<string>> solveNQueens(int n) {
dfs(n,0);
return ret;
}
void dfs(int n,int row)
{
if(row==n){
ret.push_back(path);
return;
}
//遍历每一行中每一个位置的情况
for(int i=0;i<n;i++)
{
string s(n,'.');
//剪枝
if(!col[i]&&!dig1[row-i+n]&&!dig2[row+i])
{
col[i]=dig1[row-i+n]=dig2[row+i]=true;
s[i]='Q';
path.push_back(s);
dfs(n,row+1);
s[i]='.';
path.pop_back();
col[i]=dig1[row-i+n]=dig2[row+i]=false;
}
}
}
};11. (36.) 有效的数独

这里没有用到回溯,依次遍历棋盘判断数独是否有效,所以难点在于如何剪枝。采取三个bool数组来判断该行、列、区域数字是否出现过
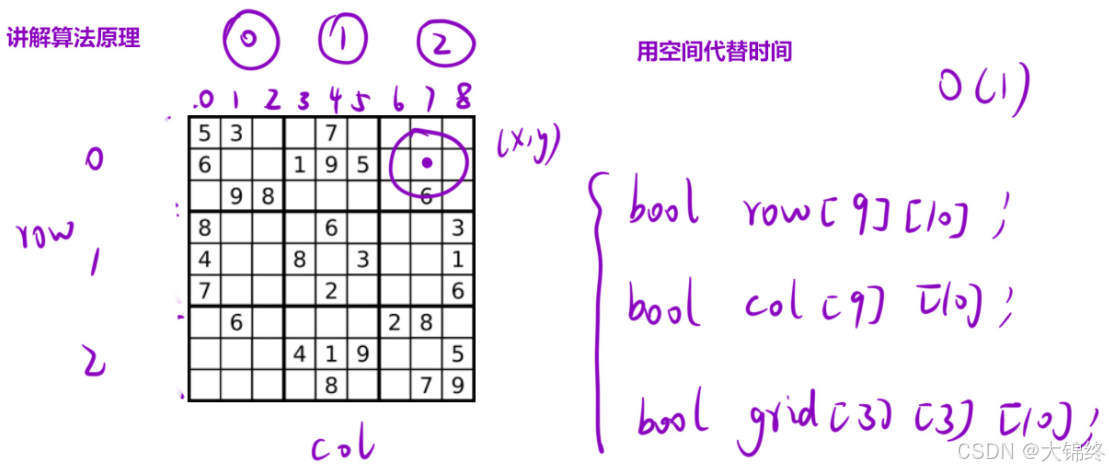
grid细节,将棋盘中三个坐标看为一个数组下标,棋盘中这三个位置除3都等于该数组下标,所以能很好区分
cpp
class Solution {
bool row[9][10],col[9][10],grid[3][3][10];
public:
bool isValidSudoku(vector<vector<char>>& board) {
for(int i=0;i<9;i++)//遍历棋盘中每一个元素
for(int j=0;j<9;j++)
{
if(board[i][j]=='.') continue;//只判断有效数字
else if(!row[i][board[i][j]-'0']&&!col[j][board[i][j]-'0']&&!grid[i/3][j/3][board[i][j]-'0'])
{
row[i][board[i][j]-'0']=col[j][board[i][j]-'0']=grid[i/3][j/3][board[i][j]-'0']=true;//标记被使用过了
}
else return false;
}
return true;
}
};12. (37.) 解数独

与上题相同定义三个bool数组来记录每个数字在目标区域中是否出现过。比上题多出递归和回溯的步骤。
1.首先在创建的三个标识数组中对棋盘中已出现的数字进行标记
2.dfs函数设置bool返回值,告诉上一层我是否能填入数字,如果填不了就恢复现场,证明第一次填入的数就错了,重新遍历下一个数进行尝试
3.本题中,我们需要直接修改给出的数组,因此在找到⼀种可行的方法时,应该停止递归,以防止正确的方法被覆盖。
cpp
class Solution {
bool row[9][10],col[9][10],grid[3][3][10];
public:
void solveSudoku(vector<vector<char>>& board) {
for(int i=0;i<9;i++)
for(int j=0;j<9;j++)
{
if(board[i][j]!='.')
{
int c=board[i][j]-'0';
row[i][c]=col[j][c]=grid[i/3][j/3][c]=true;
}
}
dfs(board);
}
bool dfs(vector<vector<char>>& board)
{
for(int i=0;i<9;i++)
for(int j=0;j<9;j++)
{
if(board[i][j]=='.')
{
for(int k=1;k<=9;k++)//遍历每一个位置能填入什么
{
if(!row[i][k]&&!col[j][k]&&!grid[i/3][j/3][k])
{
board[i][j]=k+'0';
row[i][k]=col[j][k]=grid[i/3][j/3][k]=true;
bool ret=dfs(board);
if(ret==false)
{
board[i][j]='.';//恢复现场
row[i][k]=col[j][k]=grid[i/3][j/3][k]=false;
}
else return true;
}
}
return false;//该位置所有数都填不了,证明前面填错了
}
}
return true;
}
};13. (79.) 单词搜索
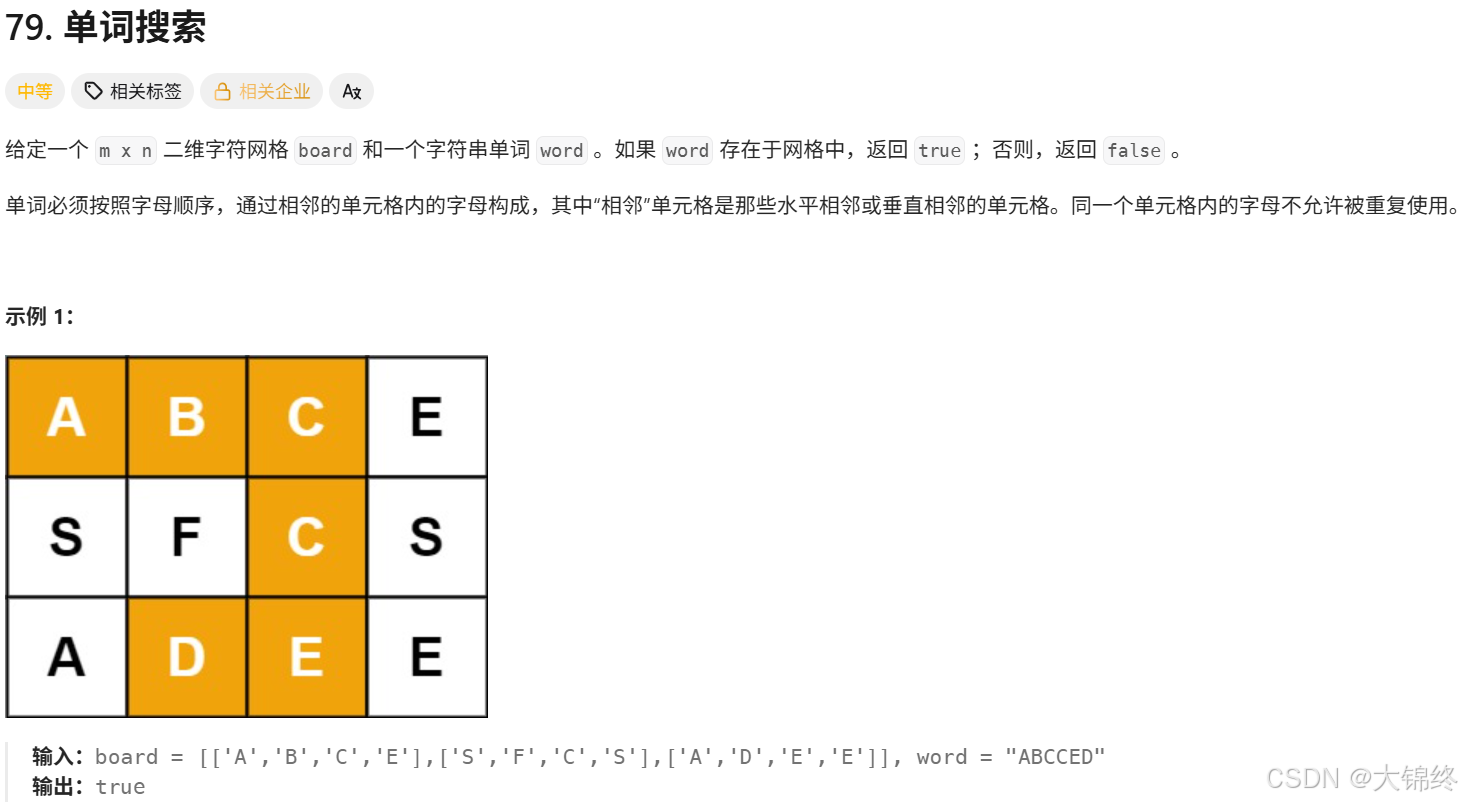
思路:
这是二维数组的dfs问题,根据题目要求只能往上下左右四个相邻的位置去寻找,不能斜线找,那么就可以定义一个向量组来表示一个位置四周的变化范围,先找到二维数组中与字符串中第一个字符匹配的位置,再基于这个位置进行dfs搜索,定义一个pos变量代表字符串中的下标,每次查找时根据变化的坐标是否符合条件、该位置元素是否使用过、二维数组中该位置元素与目标字符是否相等来剪枝,dfs的返回条件是pos位置等于字符串长度时,证明查找到了单词的完整路径
细节:
二维矩阵搜索中不能走重复的路,可以定义一个与矩阵大小相等的visit布尔数组来标记对应位置的元素是否使用过,或者直接修改原矩阵中的值,一般建议前者,多一点空间复杂度,最好不要修改原始数据
cpp
class Solution {
bool visit[7][7];//默认初始化为0
int dx[4]={1,-1,0,0};//当前位置四周的坐标变化
int dy[4]={0,0,-1,1};
int m,n;
public:
bool exist(vector<vector<char>>& board, string word) {
m=board.size();
if(!board.empty()) n=board[0].size();
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
if(board[i][j]==word[0])
{
visit[i][j]=true;
if(dfs(board,i,j,word,1)) return true;
visit[i][j]=false;
}
}
return false;
}
bool dfs(vector<vector<char>>& board,int i,int j,string& word,int pos)
{
if(pos==word.size()) return true;//该路径单词查找成功
for(int t=0;t<4;t++)//遍历四周位置
{
int x=i+dx[t],y=j+dy[t];
if(x<m&&x>=0&&y<n&&y>=0&&!visit[x][y]&&board[x][y]==word[pos])//剪枝
{
visit[x][y]=true;//标记该元素已经使用过不能再查找
if(dfs(board,x,y,word,pos+1)) return true;
visit[x][y]=false;//恢复现场
}
}
return false;
}
};14. (1219.) 黄金矿工

思路:
与单词搜索思路大致相同,都是矩阵中朝四周位置进行dfs遍历,同样运用向量数组来表示四周坐标、用vis数组来标记该位置元素是否被使用过,该题需要记录每条路径上位置值的累加,并在dfs后用max进行判断更新最大值。
所以从每个非0位置依次进行dfs再不断更新最大值即可得到答案
cpp
class Solution {
bool vis[15][15];
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
int m,n;
int ret;
public:
int getMaximumGold(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size();
int path=0;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{//遍历每个非0位置依次进行dfs
if(grid[i][j]>0)
{
vis[i][j]=true;
dfs(grid,i,j,path+grid[i][j]);
vis[i][j]=false;//恢复现场
}
}
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j,int path)
{
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&& grid[x][y]!=0)
{
vis[x][y]=true;
dfs(grid,x,y,path+grid[x][y]);//注意不能是+=否则无法自动恢复现场,要使用值传递
vis[x][y]=false;//恢复现场
}
}
ret=max(ret,path);//更新最大值
return;
}
};15 .(980.) 不同路径 III

思路:
二维矩阵的dfs,利用向量数组来表示四周坐标,本题注意每一个无障碍方格都要通过,可以用vis数组来标记每个无障碍位置是否被使用过了,也是dfs中的返回条件判断,满足总路径数就加1,否则不算,重新dfs。
有两种判断方式:
1.遍历vis数组,看每个无障碍方格所对应的bool值是否为true,即被使用过
cpp
class Solution {
int ret;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
bool vis[20][20];
int m,n;
public:
int uniquePathsIII(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size();
//找到起始方格
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
if(grid[i][j]==1)
{
vis[i][j]=true;
dfs(grid,i,j);
}
}
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j)
{
if(grid[i][j]==2)
{
for(int k=0;k<m;k++)
for(int t=0;t<n;t++)
{
if(grid[k][t]==0&&vis[k][t]==false) return ;//判断每一个无障碍房费是否使用过
}
ret+=1;//全部使用过证明该条路径合法,总数加1
return ;
}
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&grid[x][y]!=-1)//剪枝
{
vis[x][y]=true;
dfs(grid,x,y);
vis[x][y]=false;//恢复现场
}
}
return ;
}
};2.用step变量来记录原矩阵中无障碍方格有多少个,dfs传参时多传一个count变量来记录dfs的步数,如果step与count相等证明路径合法
cpp
class Solution {
int ret;
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
bool vis[20][20];
int m,n,step;
public:
int uniquePathsIII(vector<vector<int>>& grid) {
m=grid.size(),n=grid[0].size(),step=0;
int bx=0,by=0;
//找到起始方格
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
if(grid[i][j]==1) bx=i,by=j;//记录起始位置坐标
else if(grid[i][j]==0) step++;
}
step+=2;//算上起始位置和结束位置
vis[bx][by]=true;
dfs(grid,bx,by,1);
return ret;
}
void dfs(vector<vector<int>>& grid,int i,int j,int count)
{
if(grid[i][j]==2)
{
if(count==step)
{
ret++;
return;
}
return;
}
for(int k=0;k<4;k++)
{
int x=i+dx[k],y=j+dy[k];
if(x>=0&&x<m&&y>=0&&y<n&&!vis[x][y]&&grid[x][y]!=-1)//剪枝
{
vis[x][y]=true;
dfs(grid,x,y,count+1);
vis[x][y]=false;//恢复现场
}
}
return ;
}
};总结
dfs算法原理先把解题过程的过程搜索树画出来,根据该树写出代码的基本框架,重要的是如何设计dfs函数,包括参数、函数体、判断递归出口(一定先判断终止条件再处理遍历逻辑,否则会无效多遍历一层)、如何剪枝、回溯时现场恢复、传参时选择临时变量还是全局变量的问题