【你奶奶都能听懂的算法数据结构】 第13 期 数据结构
目录
开头:
今天这一期来更新一下实战篇,就如标题所见,在竞赛算法题中,很多时候我们要使用一些数据结构来帮助我们进行对数据进行增、删、查、改的操作,前面我们在学习篇里已经学习过了一些数据结构,那为什么 要在实战篇里又要学习数据结构呢?
那当然是因为有很大的不同。前面的数据结构偏向于工程,实现起来很复杂,但是在竞赛算法中,我们追求的是速度,不可能为了实现一个数据结构,从头开始写相关的函数实现吧?
所以有了这一期算法竞赛中的数据结构,这是上半部分,我们将一起学习:顺序表、链表、双向链表、栈、队列这几个数据结构,还会介绍C++中给我们提供的相关标准模板库(STL),当然,因为是实战篇,例题一定是不会少的。那就来喽!
一.顺序表
要想学习顺序表,先要知道线性表是什么?
线性表是具有相同数据类型的 n 个数据元素的有限序列,数据中元素的逻辑关系是一一对应的
而顺序表是线性表的顺序存储方式,顺序表使用一段连续的内存空间来存储数据,可以说顺序表是线性表的一种具体实现方式。
数组就是一种顺序表
按照数组的申请空间的方式,可以分为两种:
- 数组采⽤静态分配,此时的顺序表称为静态顺序表
- 数组采⽤动态分配,此时的顺序表称为动态顺序表
因为动态分配创建的数组申请空间会有时间的开销,所以在算法竞赛中,我们一般会创建一个足够大的静态数组
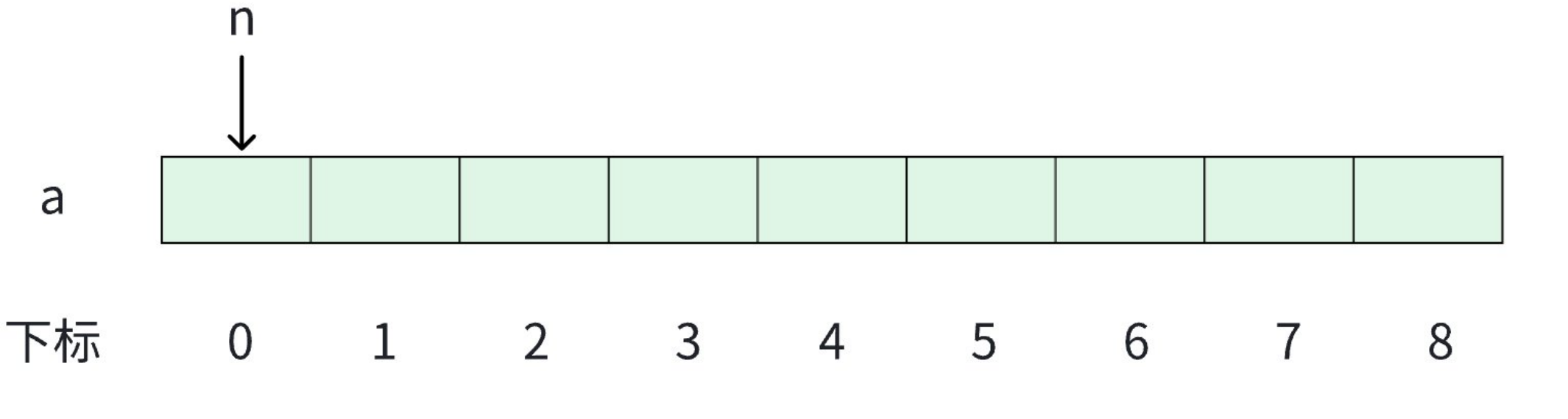
由于实现方式很简单,所以这里不做解释
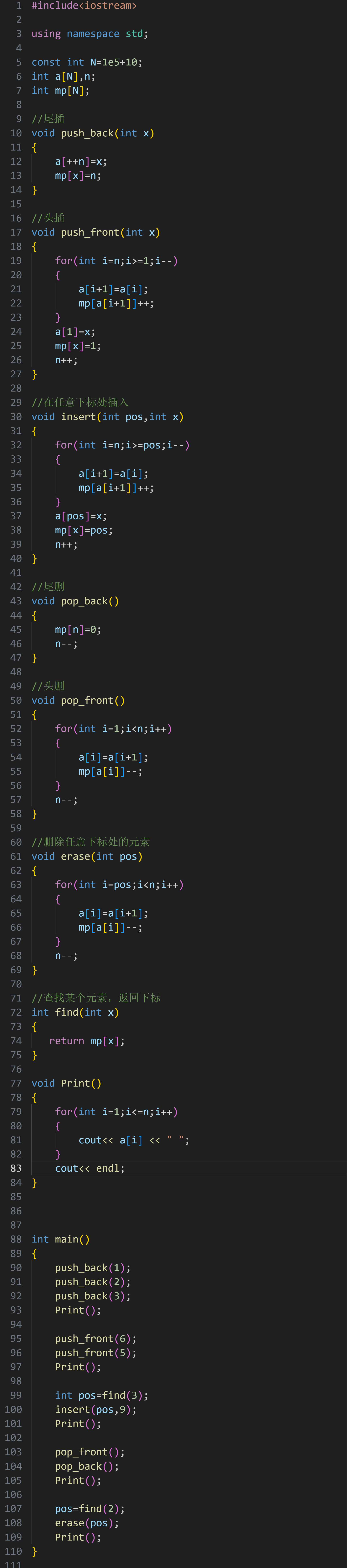
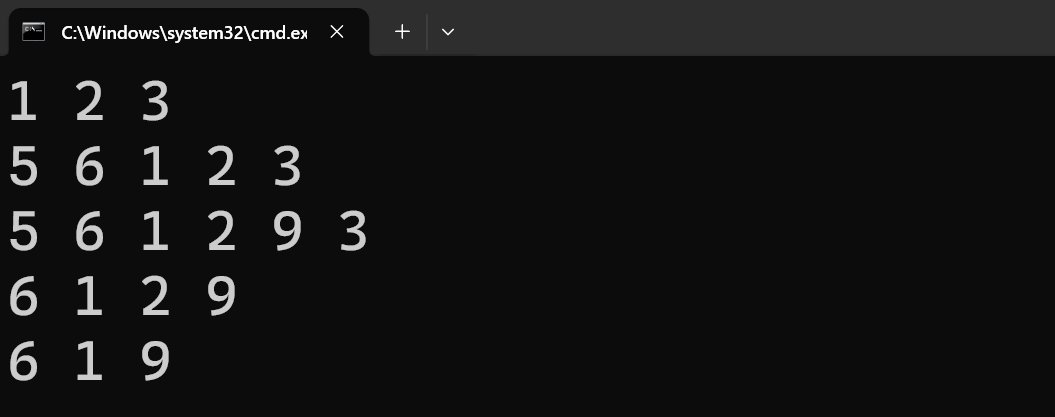
1.实现方式
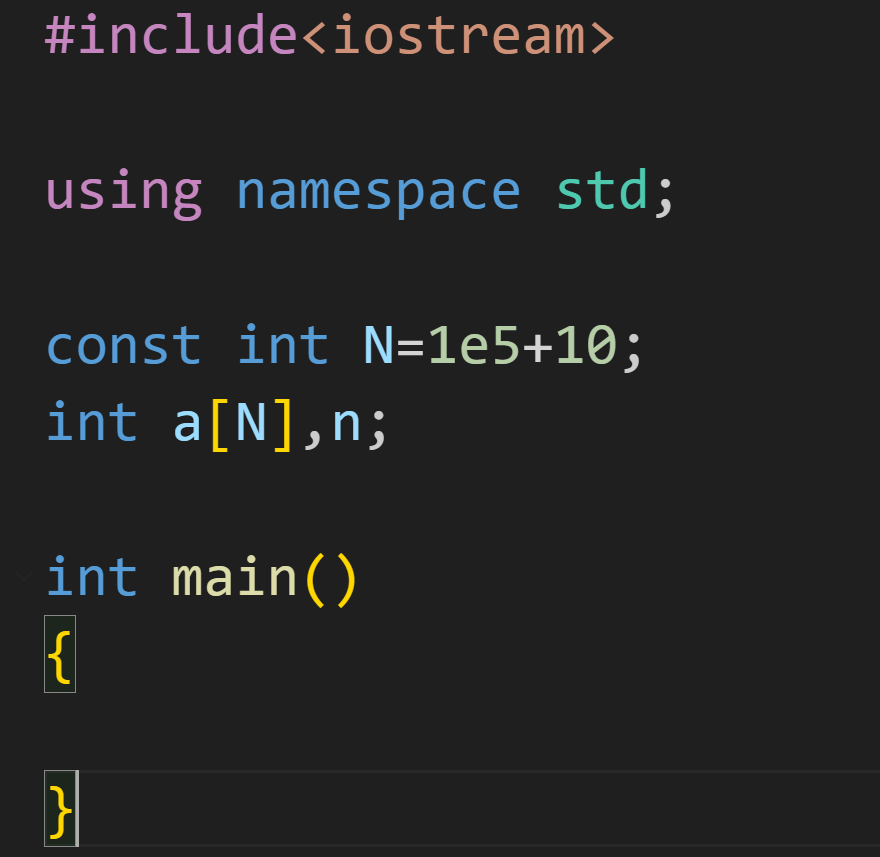
尾插:

头插

在任意下标处插入

尾删

头删

删除任意下标处的元素
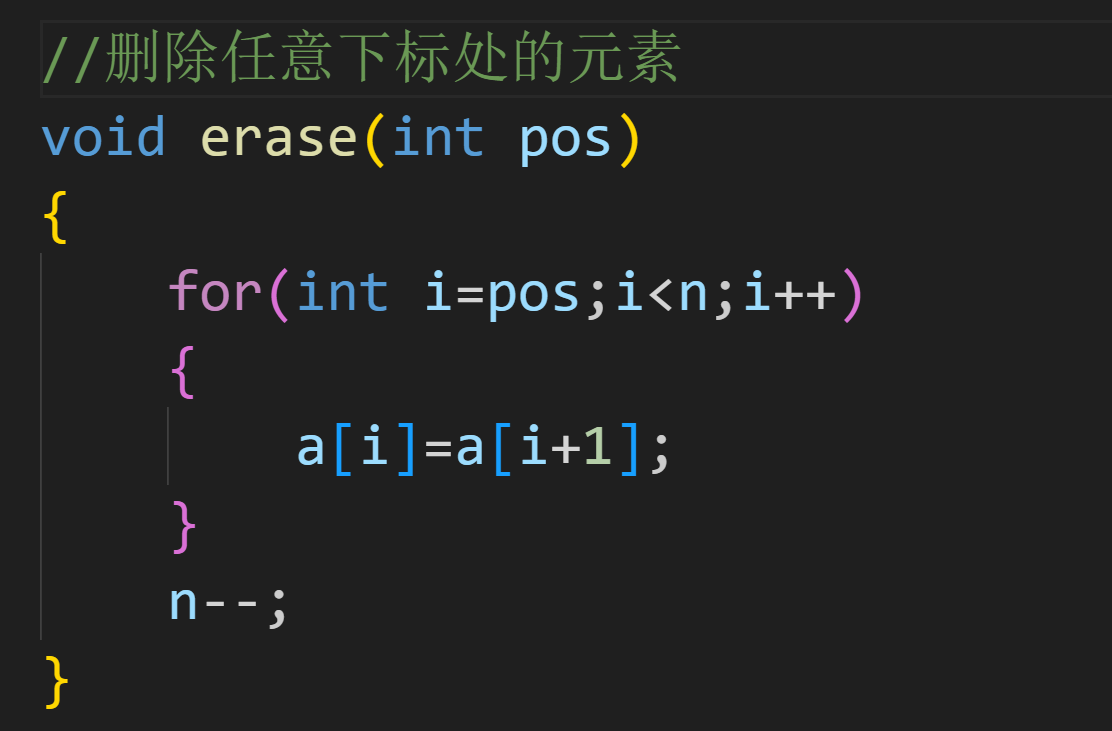
查找某个元素,返回下标

这样的查找的方法时间复杂度是 O(n),在竞赛中我们可以采用空间换时间的策略
开一个 mp 查询数组,每一次插入、删除数据的时候,也要相应的修改 mp 数组
2.STL_vector
如果需要⽤动态顺序表,有更好的⽅式: C++ 的 STL 提供了⼀个已经封装好的容器 - vector ,
有的地⽅也叫作可变⻓的数组。 vector 的底层就是⼀个会⾃动扩容的顺序表,其中创建以及增删查改等等的逻辑已经实现好了,并且也完成了封装
vector 创建的数组初始值为0
接下来重点学习一下 vector 的使用:

首先当然是要包含下头文件
接着我们来看看 vector 的几种创建方式

< > 尖括号里面是要存储的数据类型,比如:int,char 或者结构体类型
后面紧跟的是此 vector 的名字
重点来解释一下 "vector<int > a(10)" 和 "vector<int> a[10]" 这两者的区别
- "vector<int > a(10)" 这个相当于是创建了一个初始大小为10的数组
- "vector<int> a[10]" 这个相当于可以看成------"变量类型 a(数组名)[大小]" 也就是说 a 数组存储的数据类型是 vector ------一个可变长数组
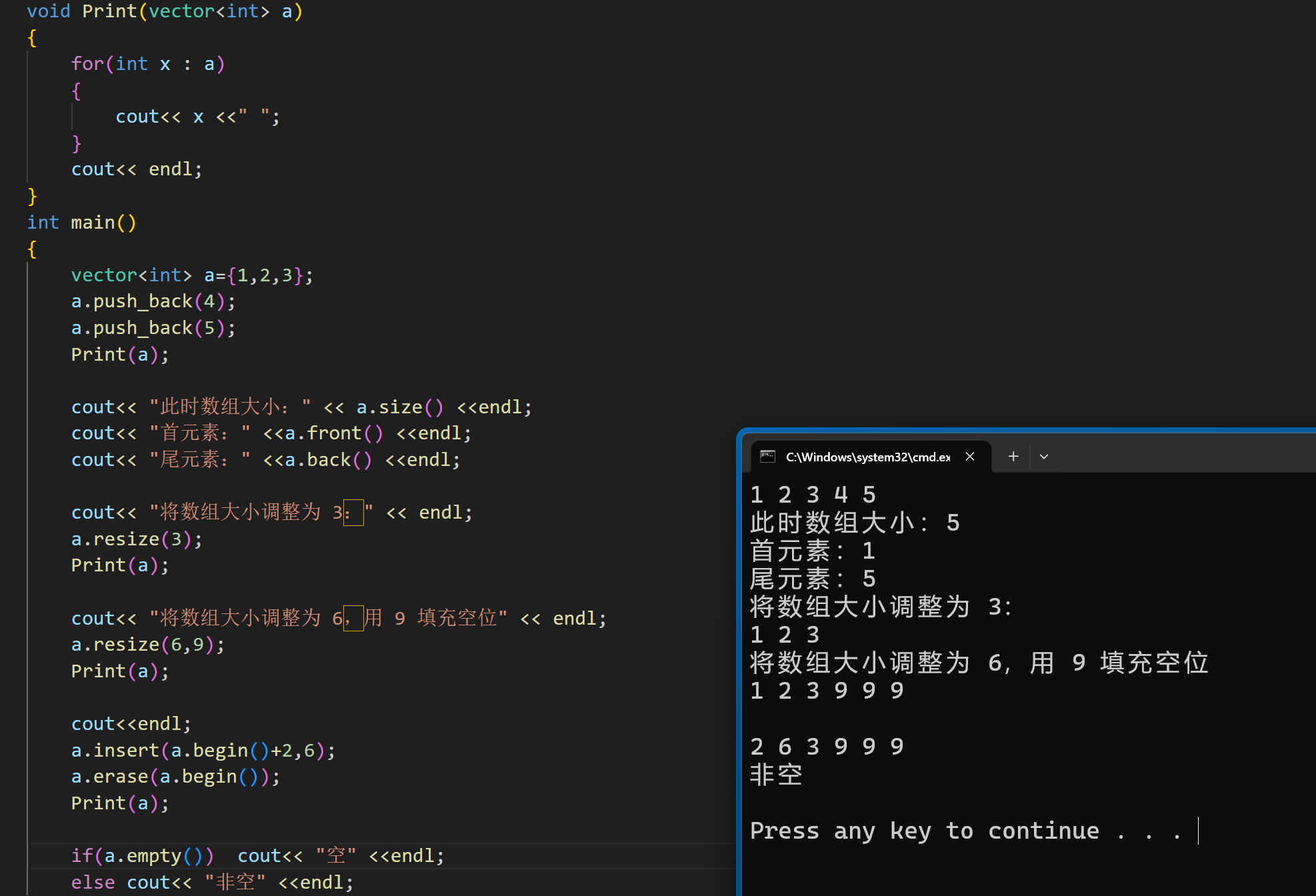
下面我们来看看 STL 提供的相关函数:

(调整元素数量 v.resize( n,val ) ,如果是扩大容量,多出来的元素用 val 填充)
3.例题
(1)芬兰国旗问题

本题要求是不能借助排序
这是经典的 "三色排序问题(芬兰国旗问题)",要将一组数按照特定的规则排列成三个大部分,还记得之前我们在双指针算法讲的移动 0 问题吗?------双指针算法
这里我们要借助三个指针将数组分成四个部分
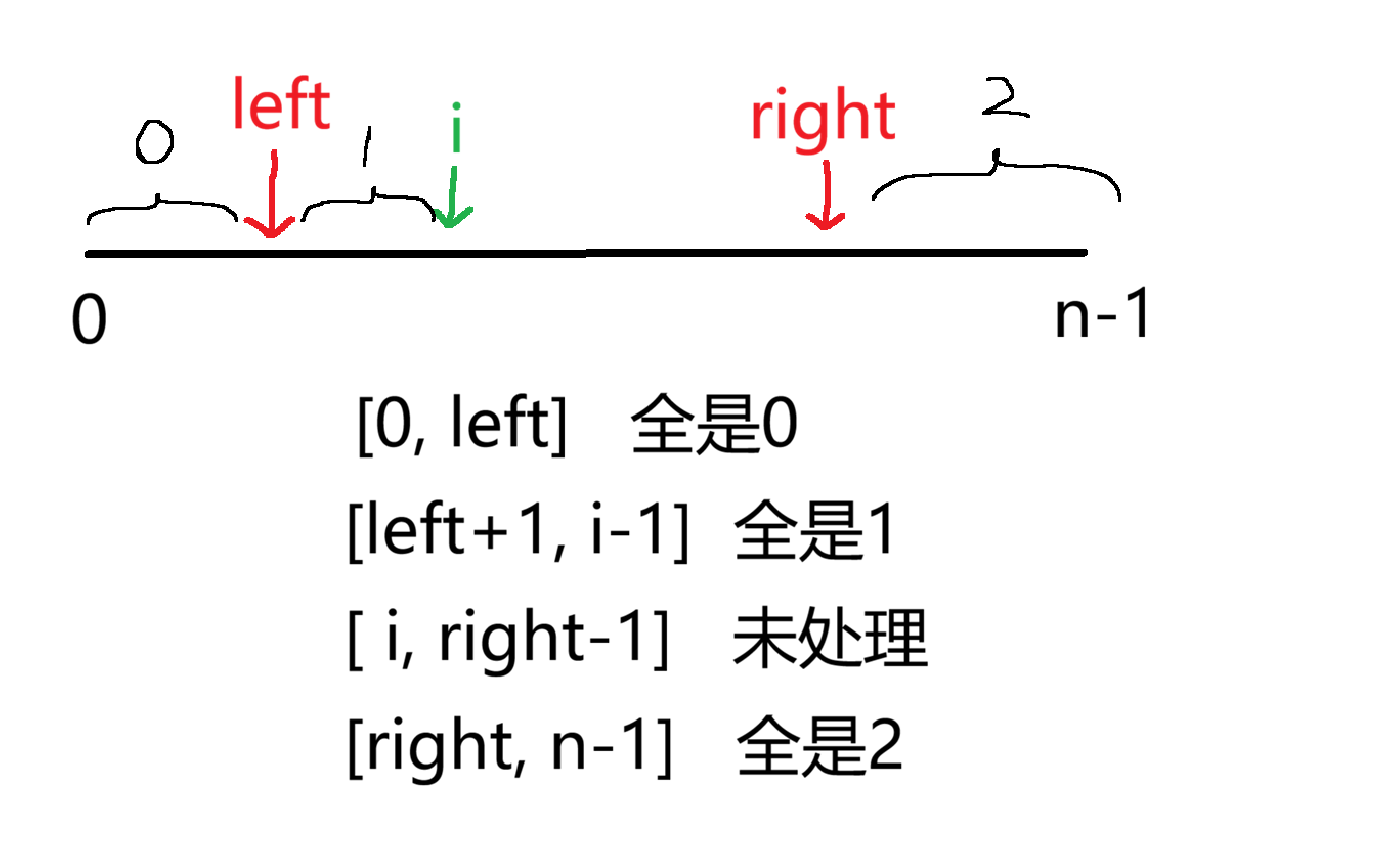
我们通过指针 i 来遍历数组,结束条件是当 i 与 right 相遇时
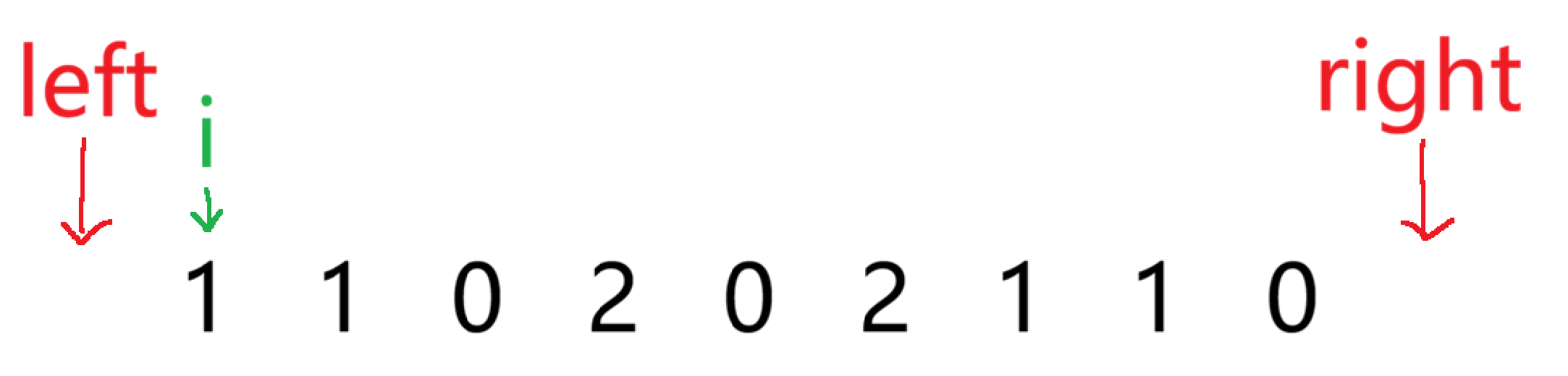
当 i 指向的数为 1 时,符合【left+1, i -1】全是1,就让 i++
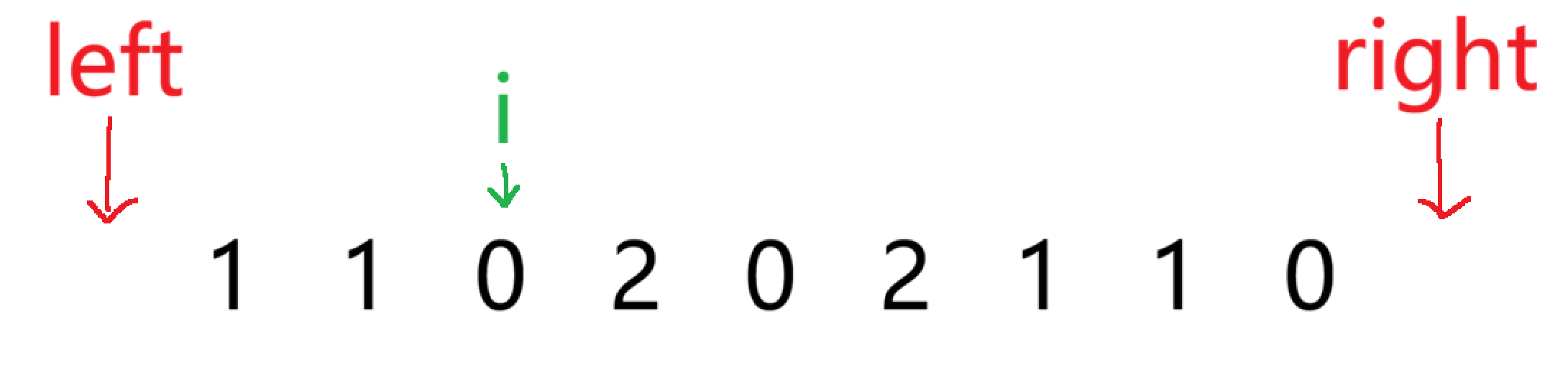
当 i 指向的数为 0 时,就要进入左区间,先 left++,再交换 left 和 i 指向的两个数,然后再 i++,继续判断
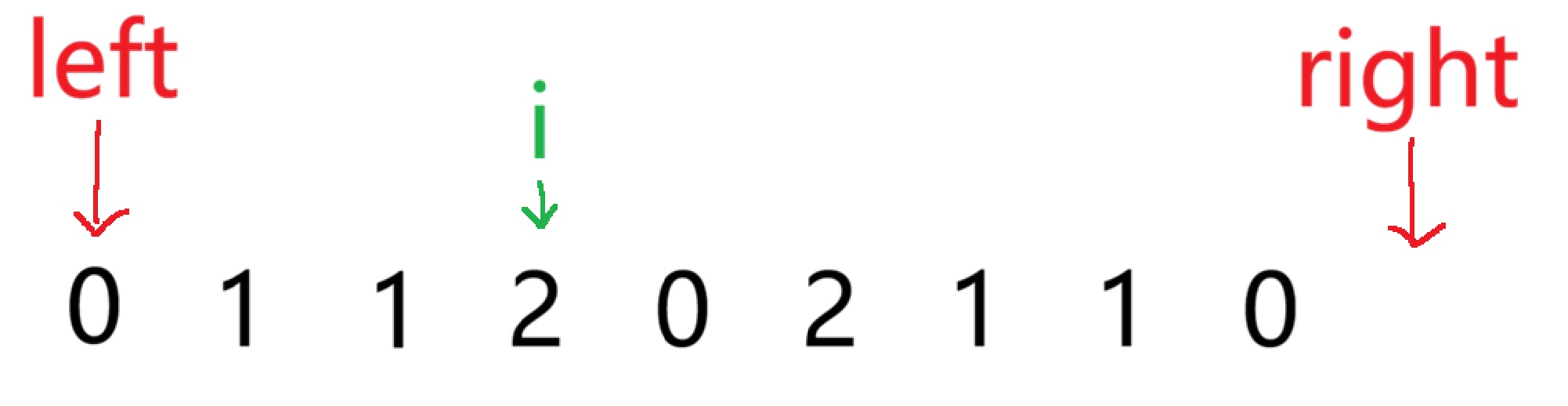
当 i 指向的数为 2 ,这时就要让这个数添加到最右区间,right--,交换此时 right 和 i 指向的数,然后 i++
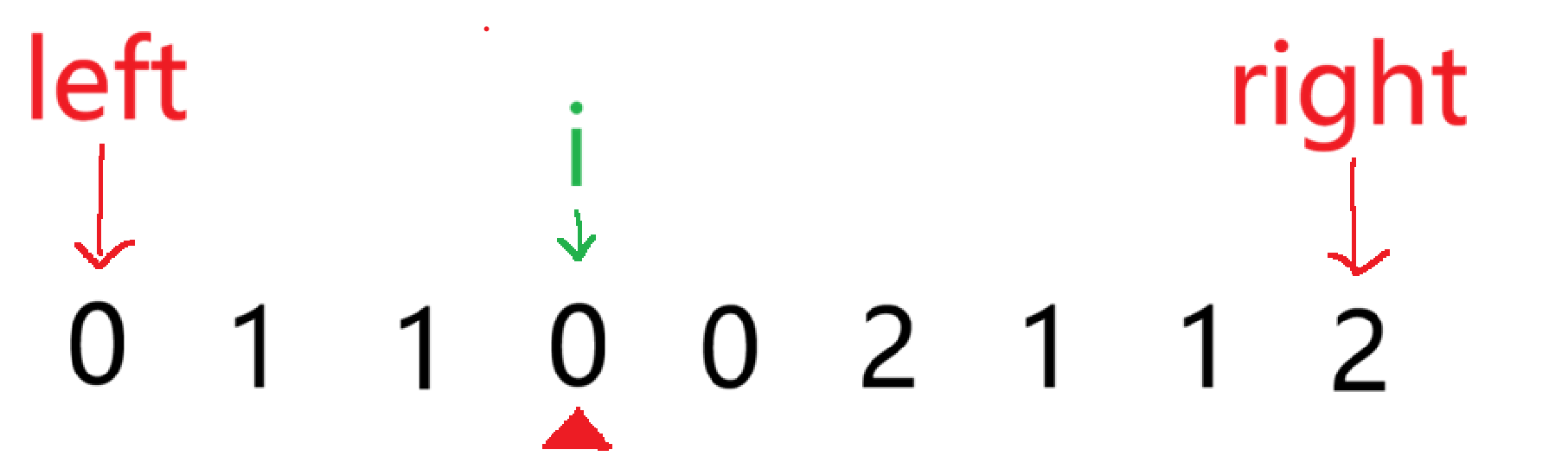
但是这会有一个问题,如图,这时候如果 i++ 的话,会将未处理范围内的一个数越过,所以这种情况下不能直接将 i++,要继续判断此时 i 指向的数
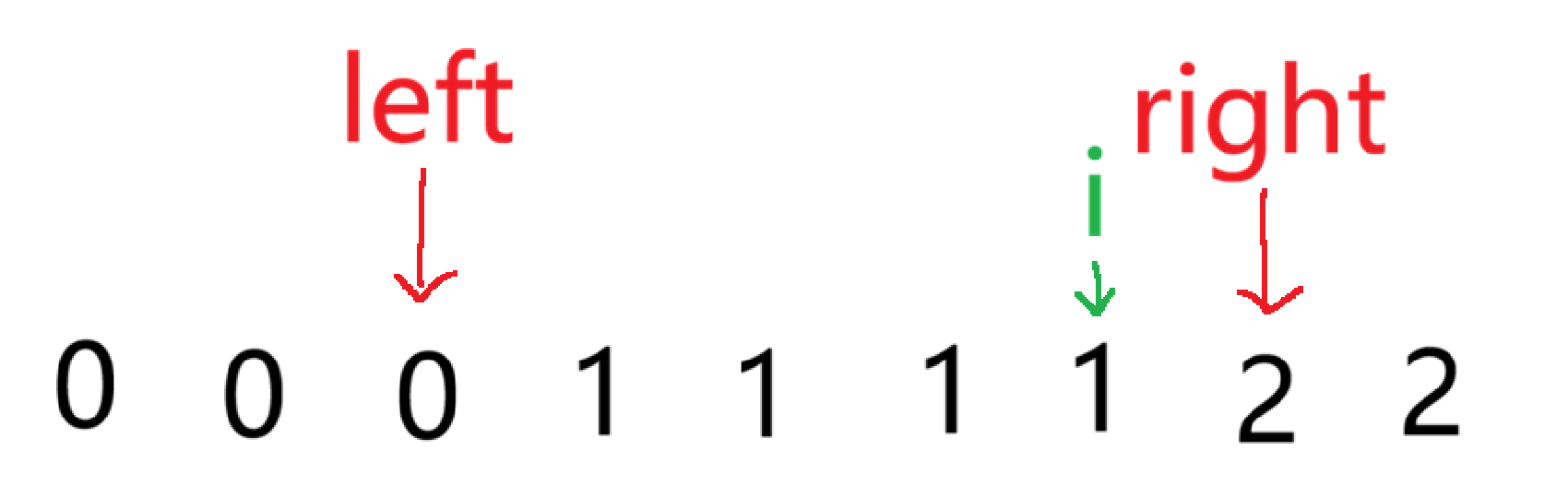
当 i 与 right 相遇时,就结束循环,这时候数组就被分成了三个部分
代码实现:
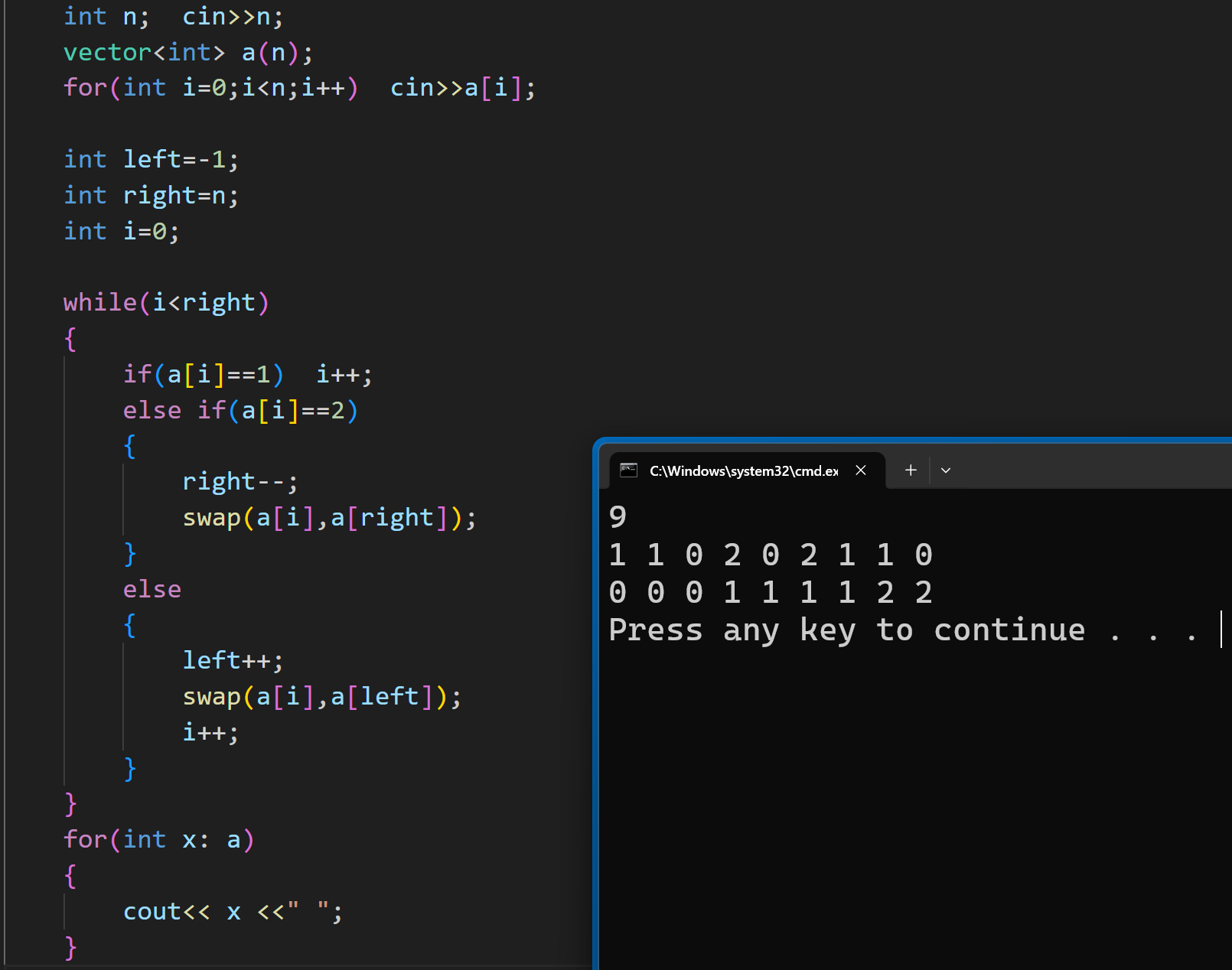
(2)移动木块

这题目又臭又长,其实简单来说就是要完成两个操作:归位、叠放
总结一下题目:
当有 "move"时,就要将 a 上的木块归位
当有 "onto"时,就要将 b 上的木块归位
最后都要将 a 及以上的放到 b 上
根据题意我们要创建一个 vector<int> a[ n ] 的数组,就拿事例举例:

先走前四步:
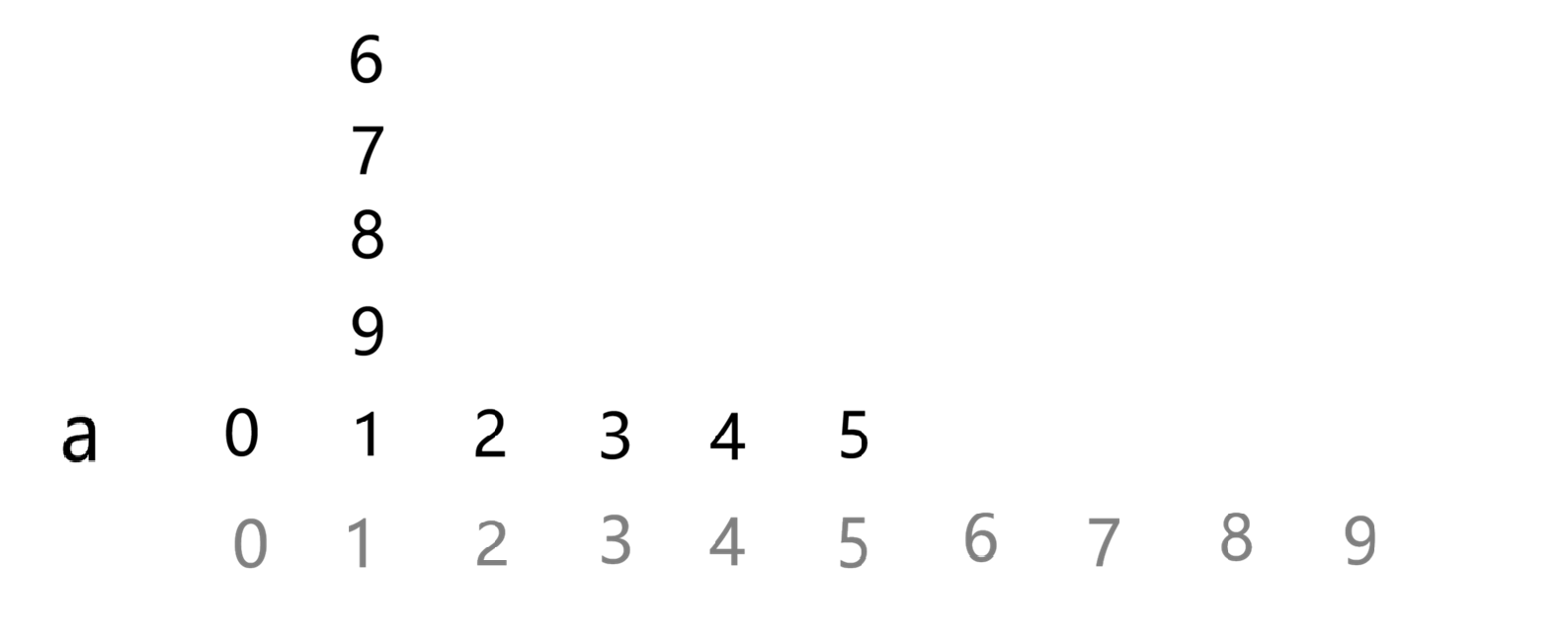
接着是:pile 8 over 6
要将 8 及它后面接的数都要放到 6 ,但是此时它们放在同一个木块上,就不用管,跳过此步
接下来是:pile 8 over 5
要将 8 及它后面接的数都要放到 5
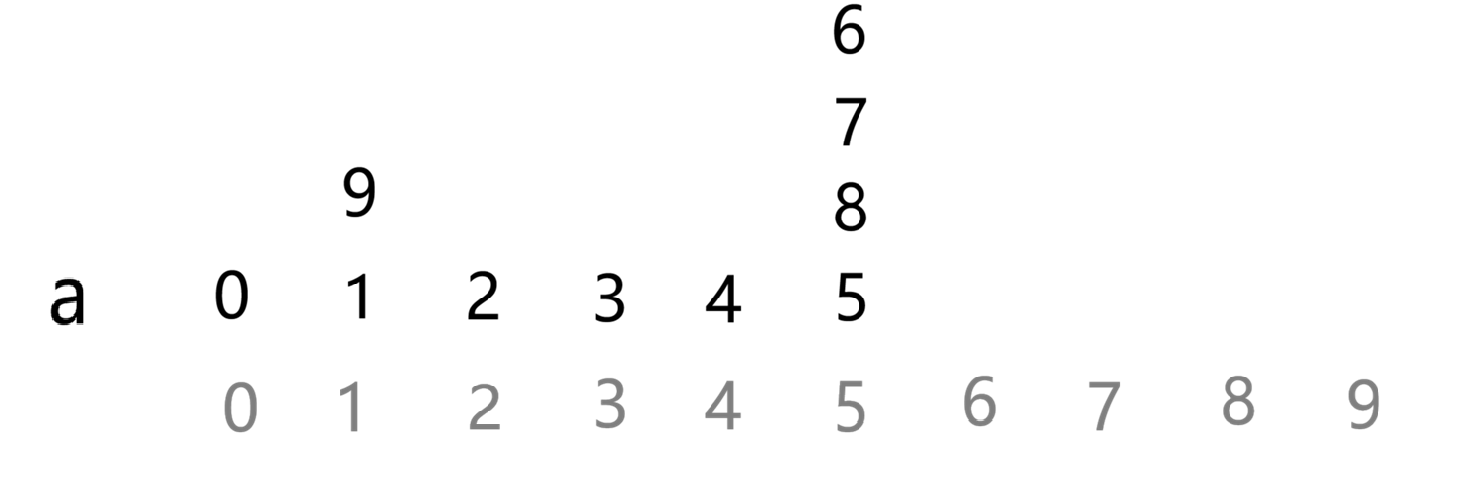
接下来的两步:
和最后的结果是一样的
解释完这是一个什么样的过程,接下来我们就要去思考,如何用代码实现归位,叠放操作
要实现归位 a 或 b 上的所有木块,首先要找到它们的位置在哪里吧,找到位置后,就可以用一个循环遍历往后的数,将他们依次尾插到本身对应的位置
要实现叠放,其实就是尾插到相应的位置
另外,要记录一个数的位置,要有两个信息,一个是在 a 数组的第几个 vector 数组中,另一个就是在此 vector 数组的第几个
就可以用 pair:
pair 是 C++ 标准库中的⼀个模板类,⽤于将两个值组合成⼀个单⼀对象,通常⽤于存储键值对或返回多个值。它有两个公有成员 first 和 second ,分别表⽰第⼀个值和第⼆个值
我们可以把 pair 理解成 C++ 为我们提供⼀个结构体,⾥⾯有两个变量:
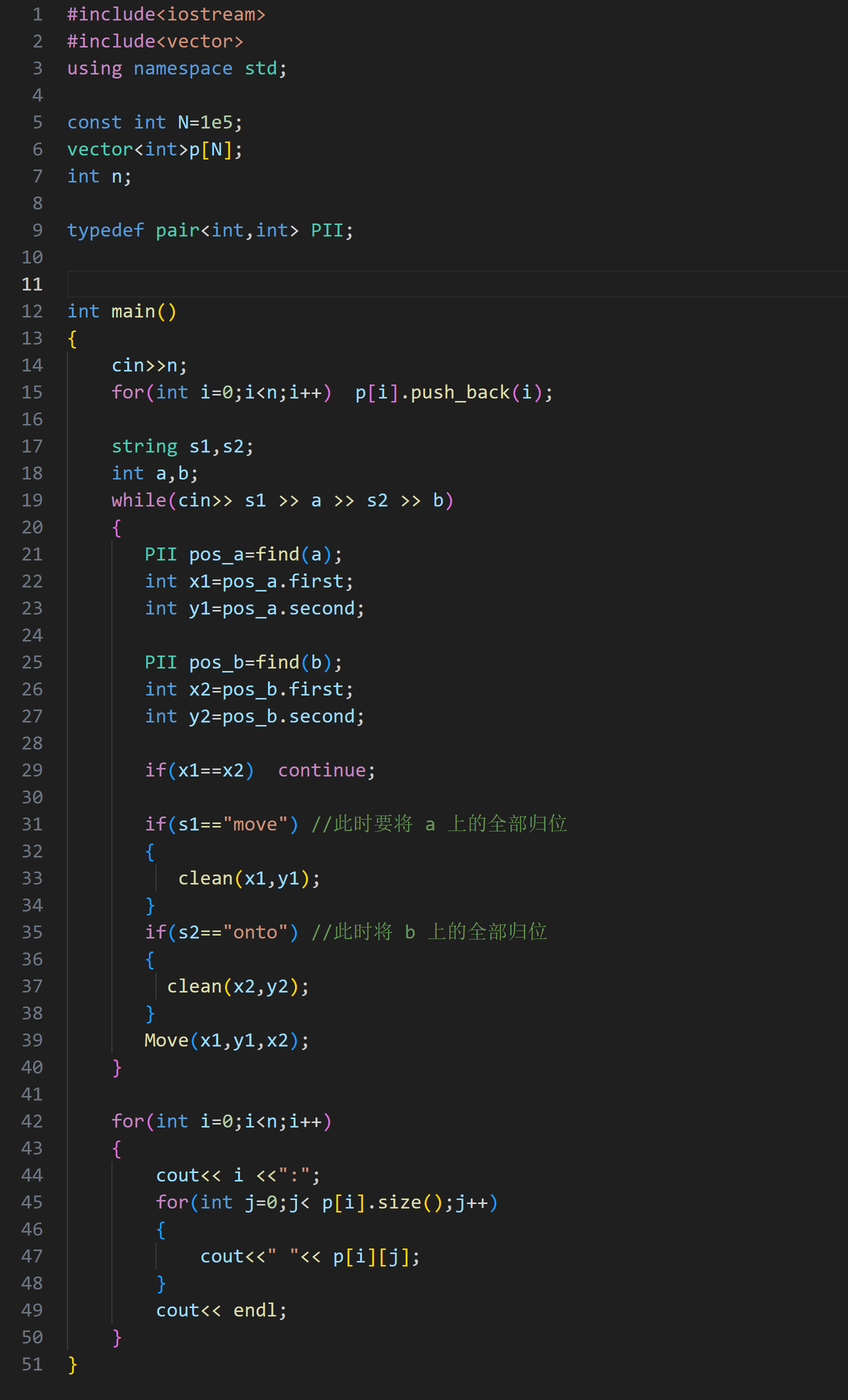
这样一个框架就搭建好了,此时我们就要来实现 find(查询)、clean(归位)、Move(叠放)这三个函数
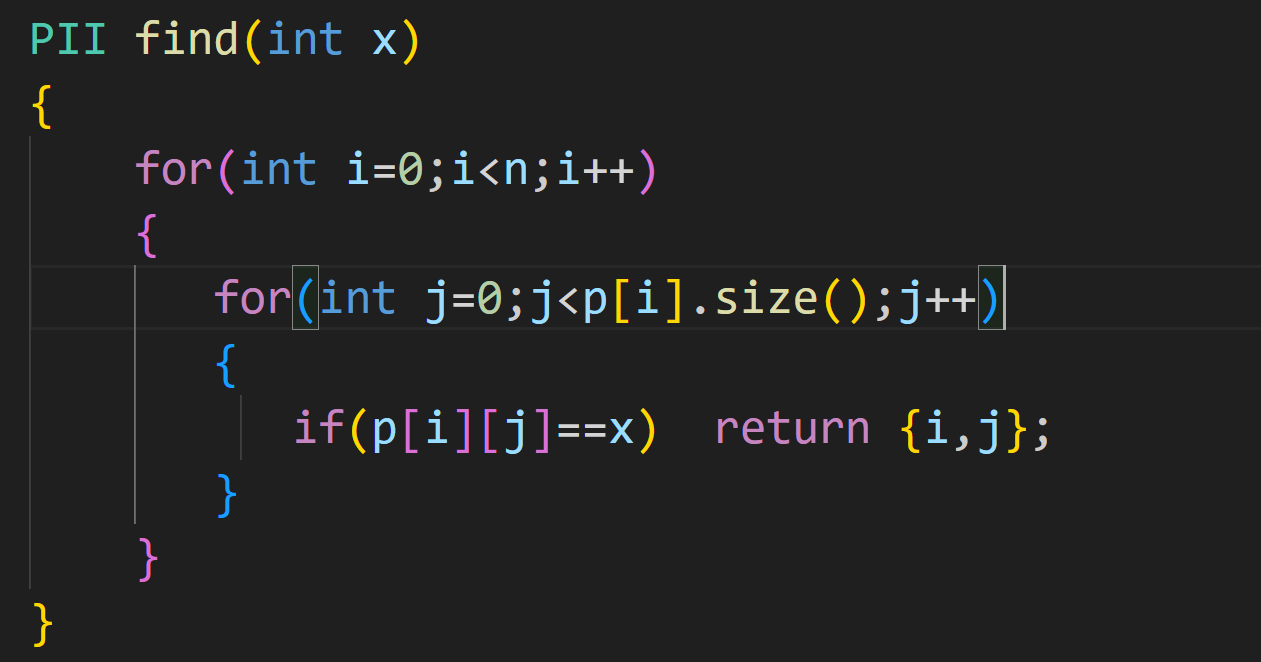
一个简简单单的循环遍历

要注意的是,归位以后,原 vector 的大小就要收缩,防止访问到已经归位的数据

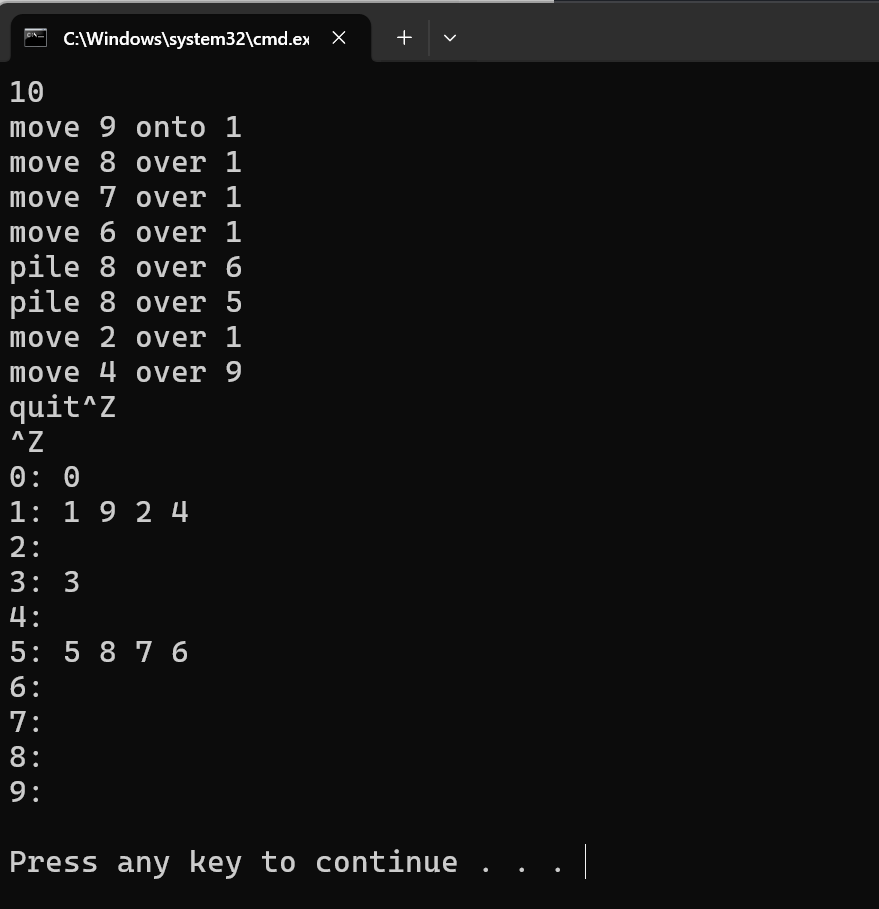
完整代码:
cpp
#include<iostream>
#include<vector>
using namespace std;
const int N=1e5;
vector<int>p[N];
int n;
typedef pair<int,int> PII;
PII find(int x)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<p[i].size();j++)
{
if(p[i][j]==x) return {i,j};
}
}
}
void clean(int x,int y)
{
for(int i=y+1;i<p[x].size();i++)
{
int t=p[x][i];
p[t].push_back(t);
}
p[x].resize(y+1);
}
void Move(int x1,int y1,int x2)
{
for(int i=y1;i<p[x1].size();i++)
{
int t=p[x1][i];
p[x2].push_back(t);
}
p[x1].resize(y1);
}
int main()
{
cin>>n;
for(int i=0;i<n;i++) p[i].push_back(i);
string s1,s2;
int a,b;
while(cin>> s1 >> a >> s2 >> b)
{
PII pos_a=find(a);
int x1=pos_a.first;
int y1=pos_a.second;
PII pos_b=find(b);
int x2=pos_b.first;
int y2=pos_b.second;
if(x1==x2) continue;
if(s1=="move") //此时要将 a 上的全部归位
{
clean(x1,y1);
}
if(s2=="onto") //此时将 b 上的全部归位
{
clean(x2,y2);
}
Move(x1,y1,x2);
}
for(int i=0;i<n;i++)
{
cout<< i <<":";
for(int j=0;j< p[i].size();j++)
{
cout<<" "<< p[i][j];
}
cout<< endl;
}
}
二.链表
单向链表
前面的学习篇我们一起手撕链表------手撕链表
在算法竞赛中,使用链表可以通过两个足够大的数组来模拟实现:
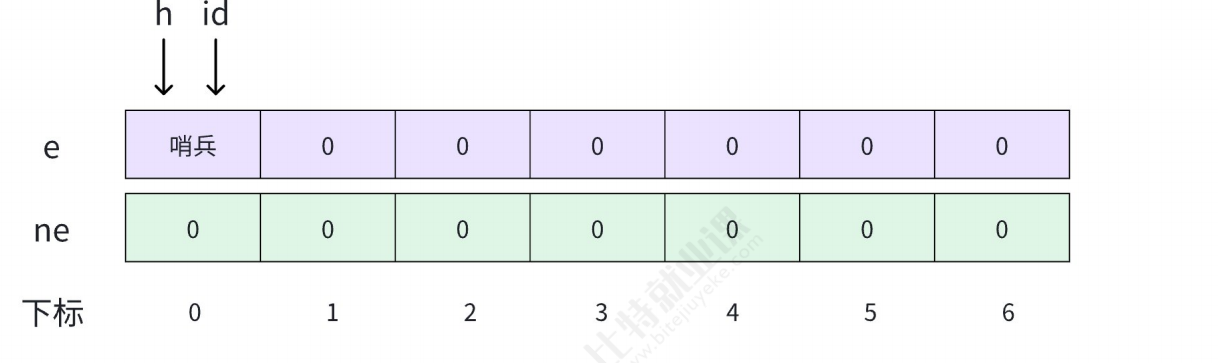
此时的下标就可以当作此前我们学习链表的地址,下标为 0 的位置当作哨兵位.
h 指针始终指向哨兵位,id 每次指向链表的尾
1.实现方式
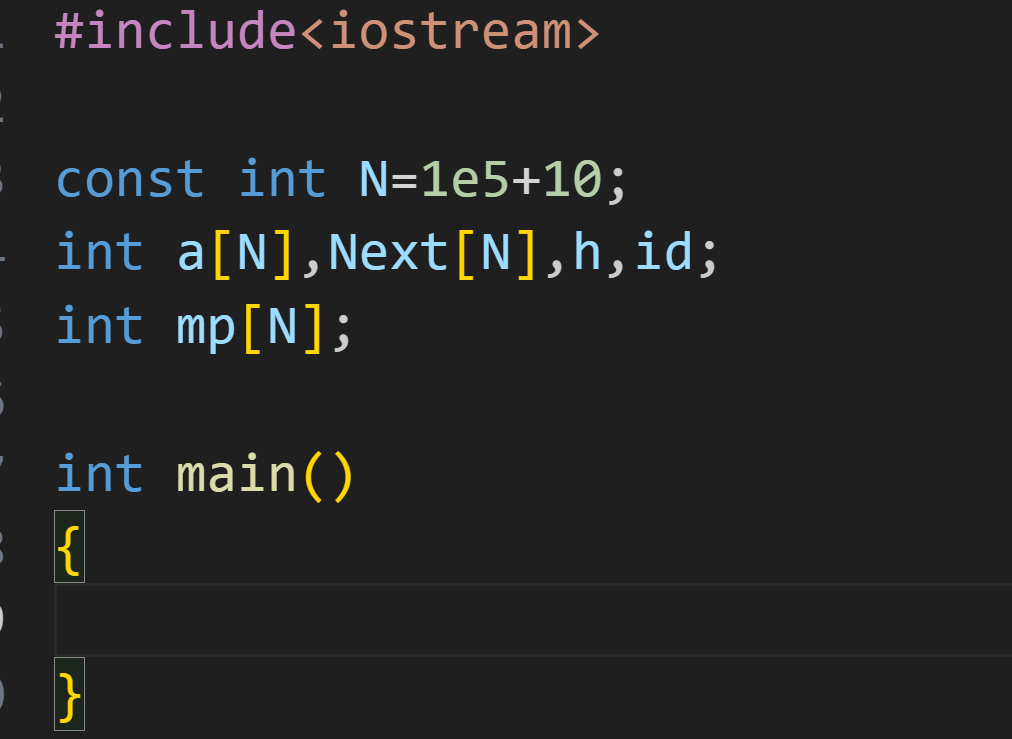
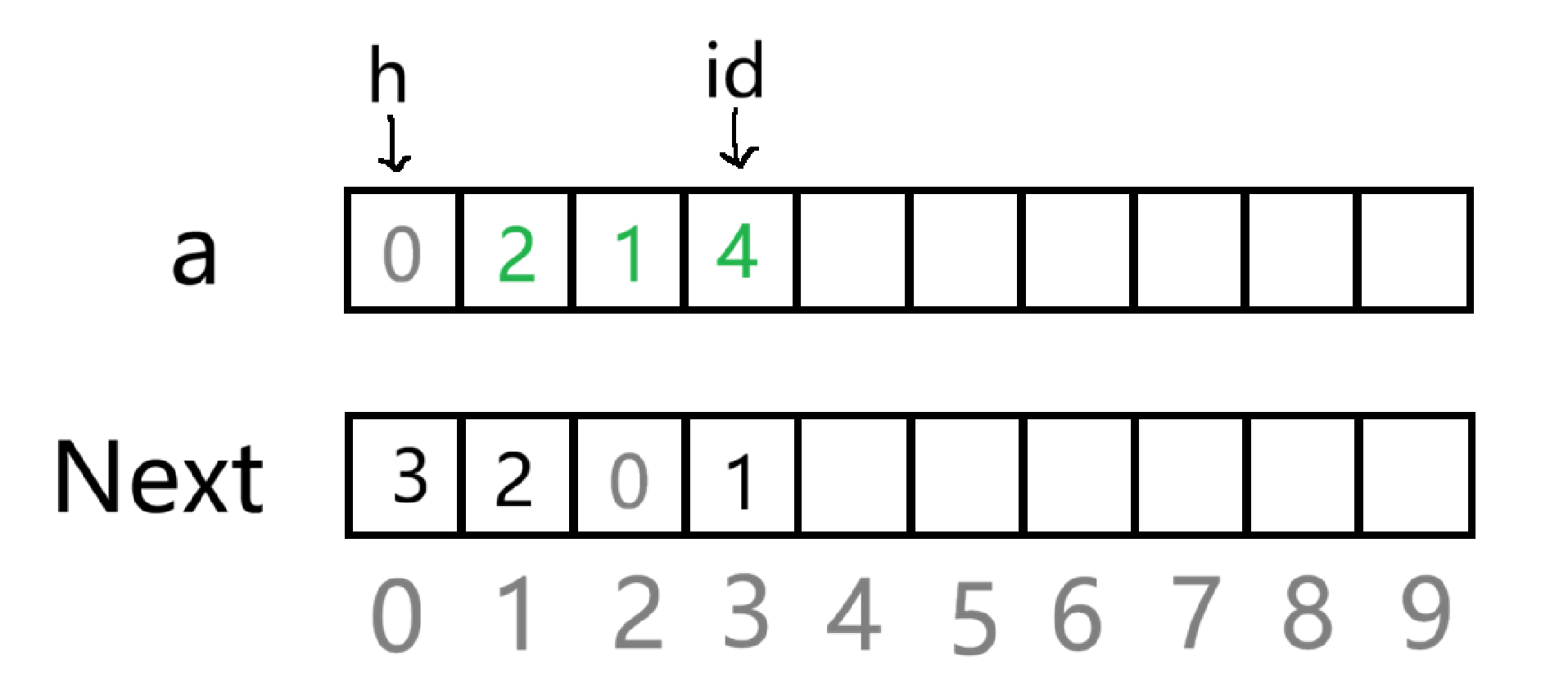
如上图,先创建了两个数组,a 数组是专门存放数据的数据域, 而 Next 是存放下一位地址(下标)的指针域
为了可以快速的访问某一个数据,可以开一个足够的数组 mp ,将数本身作为下标,存放的是其在 a 数组的下标,以此来实现快速访问
头插:
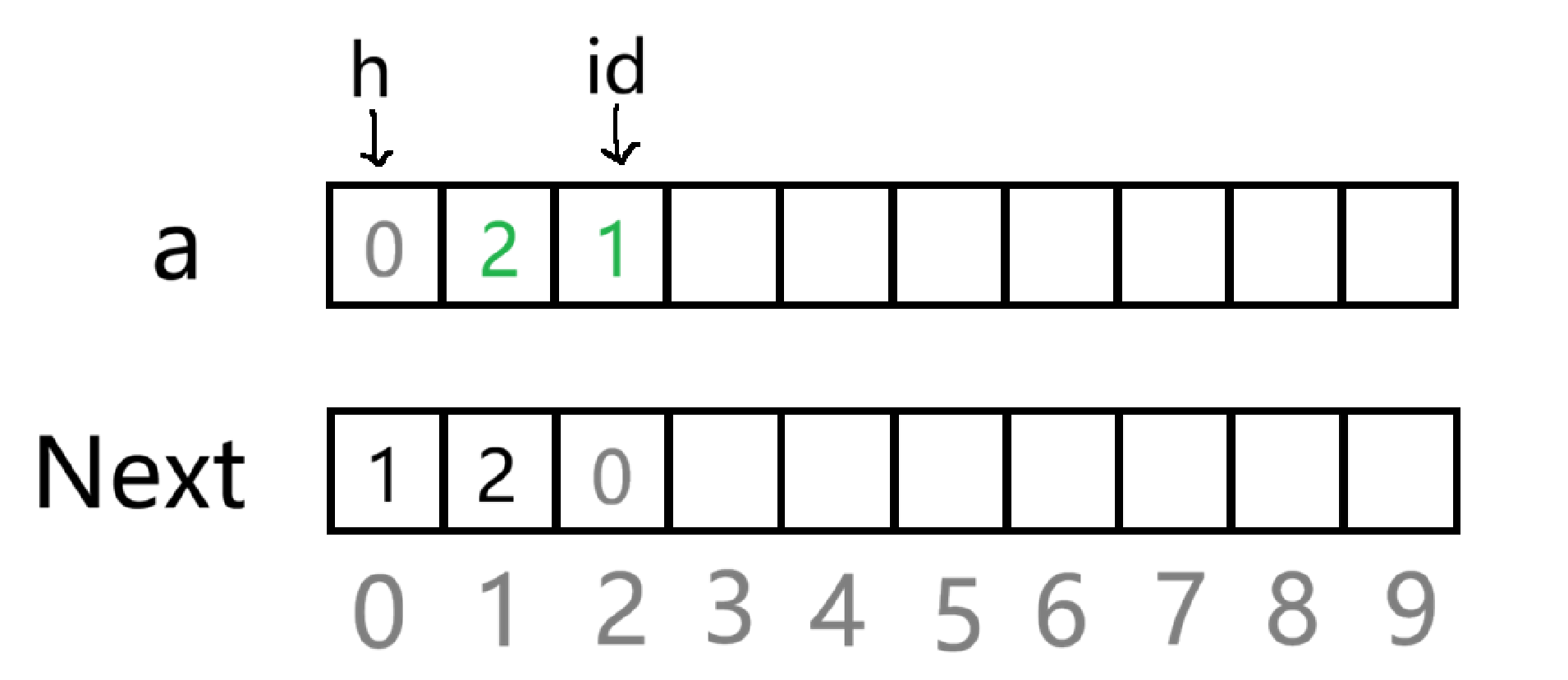
现在有这样一段初始序列,要进行头插,也就是说要插在 h 指向的哨兵位后面那一位
首先肯定是先让 id++ , 去指向一块新的空间,然后将对应位置的值赋值成要插入的值
即 a [ id ] = 4 ( 假设要将 4 进行头插)
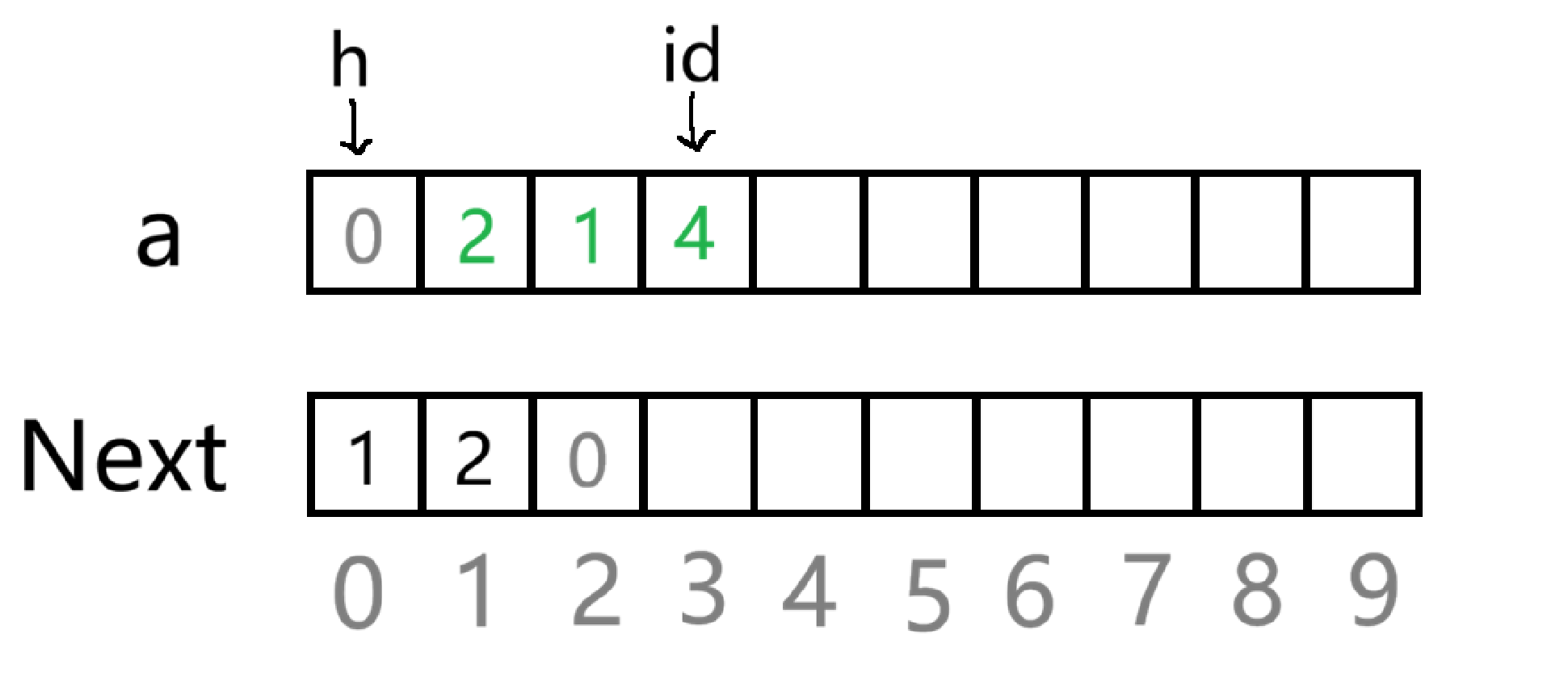
但是这样只是在数据域中申请了空间来存放值,要想在逻辑结构上进行头插,其实就和动态链表的实现一样,只不过这里的地址就是数组的下标( id )
先 Next [ id ] =Next [ h ],就是让头插进来的新元素的 Next 指向原先的头节点
再 Next [ h ] = id,就是让哨兵位的下一个指向新的头节点的地址------ id

遍历链表:
依旧和链表的循环遍历一样,直接上代码

查询:
因为我们使用了 mp 数组记录每个数据的下标信息,所以我们可以用 O(1)的时间复杂度快速查找某个值的下标
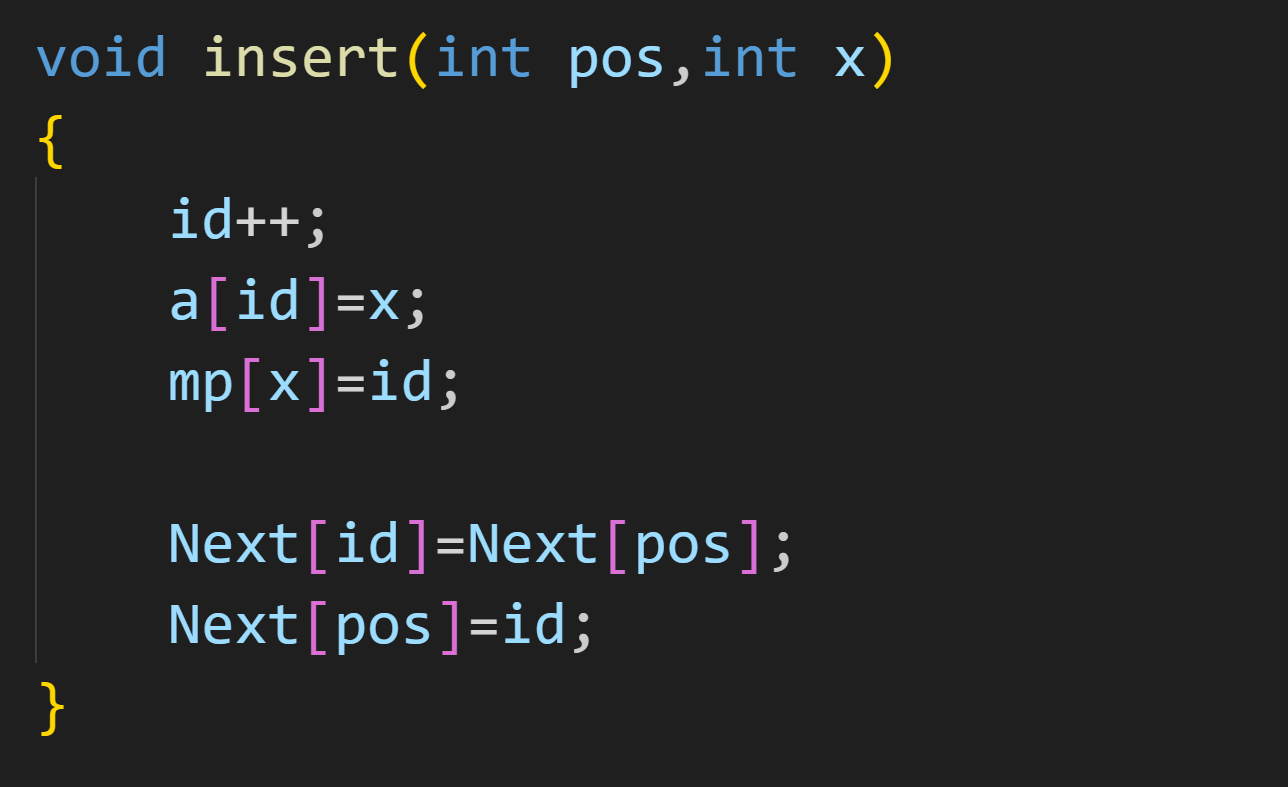
在任意位置之后插入
注意这里的 "位置" 指的是数组中的下标
要在给定的位置的后面插入( 在 2 后面插入一个 5)
首先当然是 id++ ,让 id 指向一个新的空间,接着依旧让 a [ id ] =5
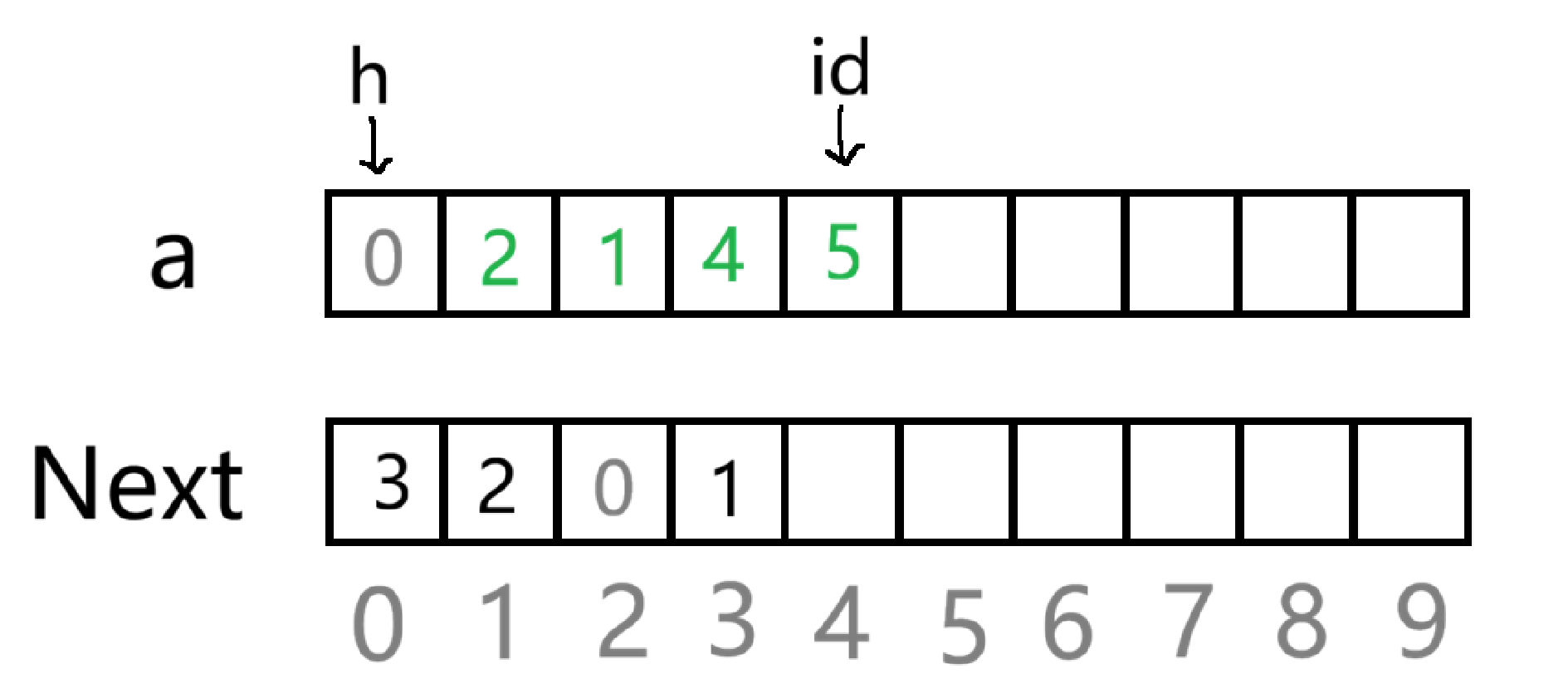
因为 2 的下标是 1 ,先让 id 申请的新的元素的 Next 指向 2 原本的后一位
即 Next [ 1 ],接着让 2 的后面指向新的元素,即 Next [1]= id
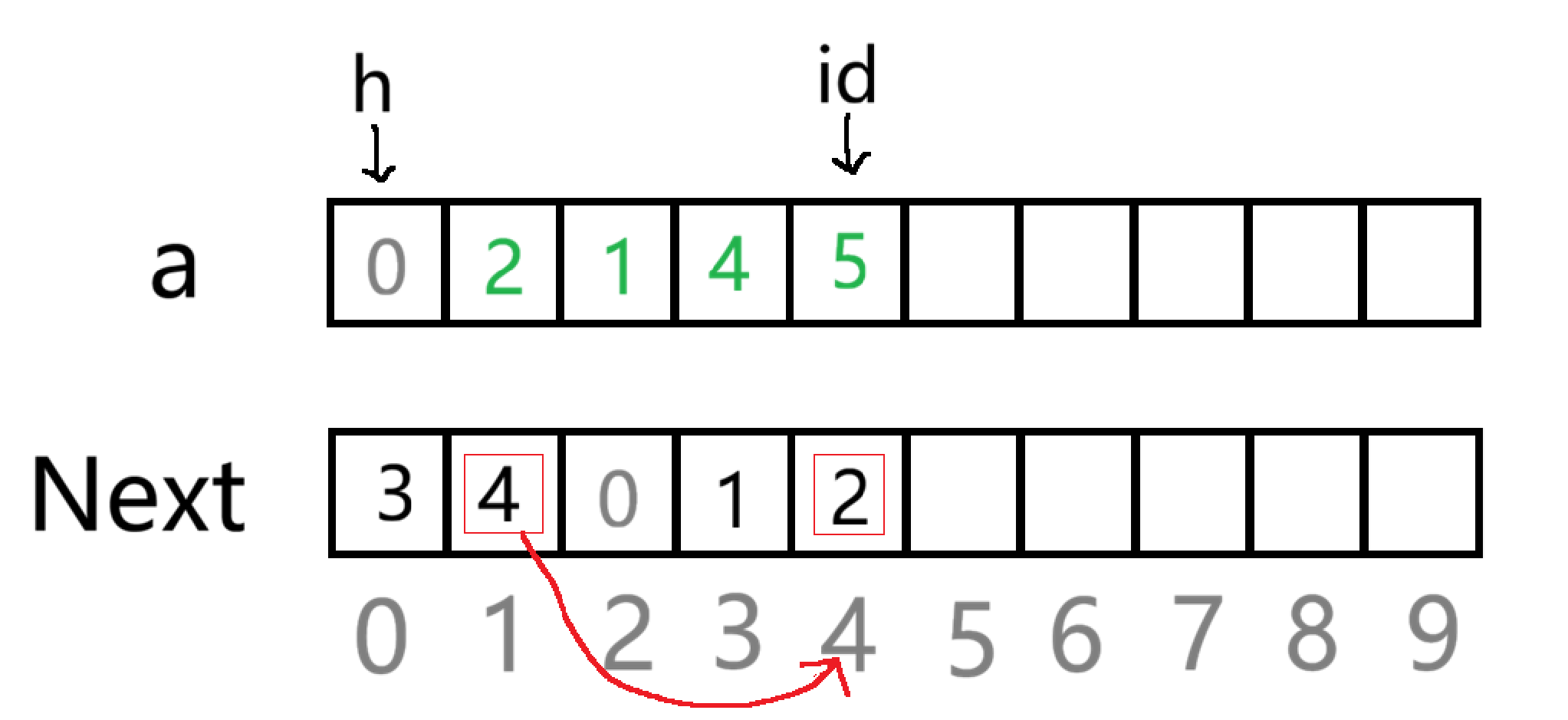
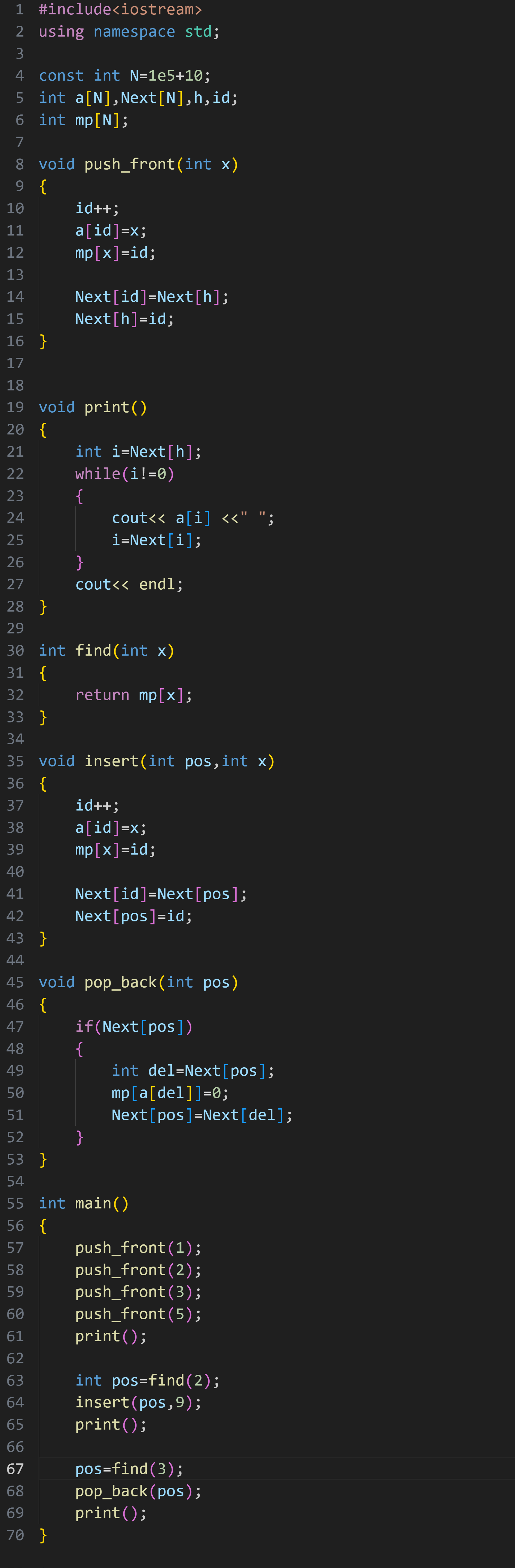
删除指定位置后的元素
首先这个位置不能是链表的末尾,如果是链表的尾元素,其 Next 指针域存的是 0,指向的是哨兵位,不能把哨兵位删了吧
所以代码是:

完整代码:
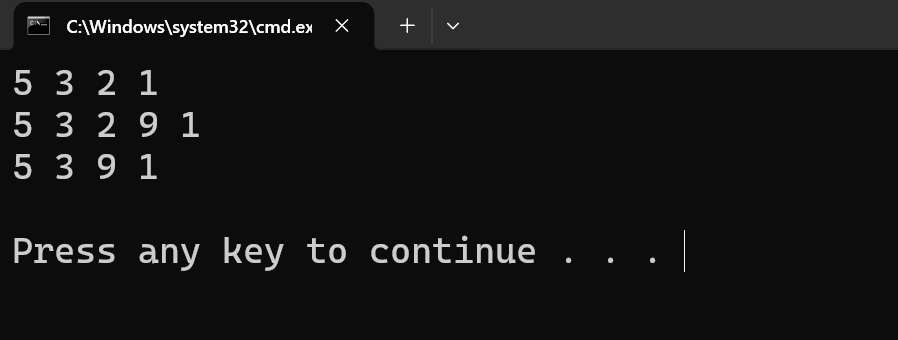
2.STL_list
C++的 STL 中也提供了关于链表的标准模板库,我们也来学习一下:
首先当然要包含头文件

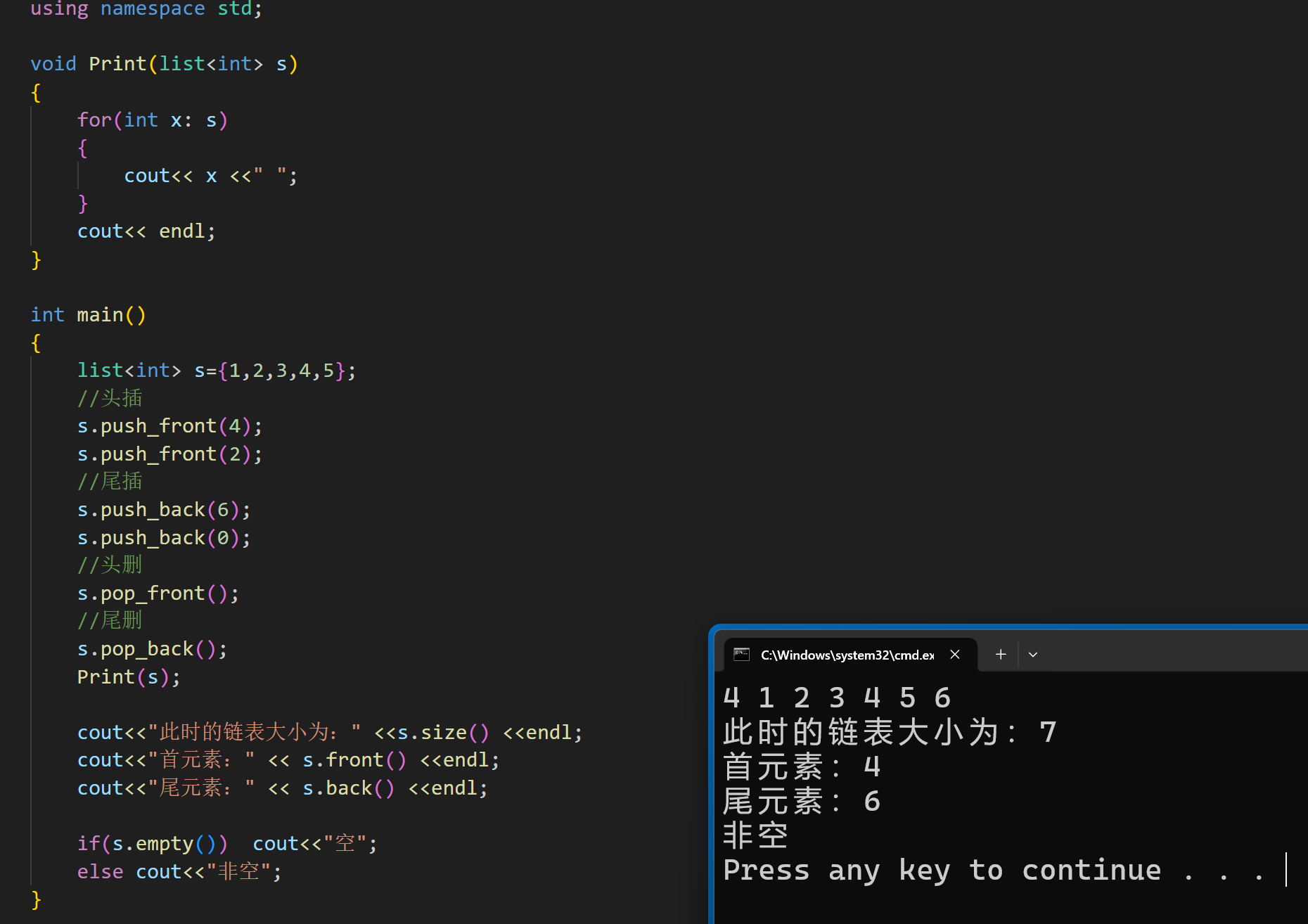
初始化:

如上图,有两种初始化方式,可以直接初始化,也可以放几个值进行初始化
< > 尖括号里面依旧是存储的变量类型
相关函数:
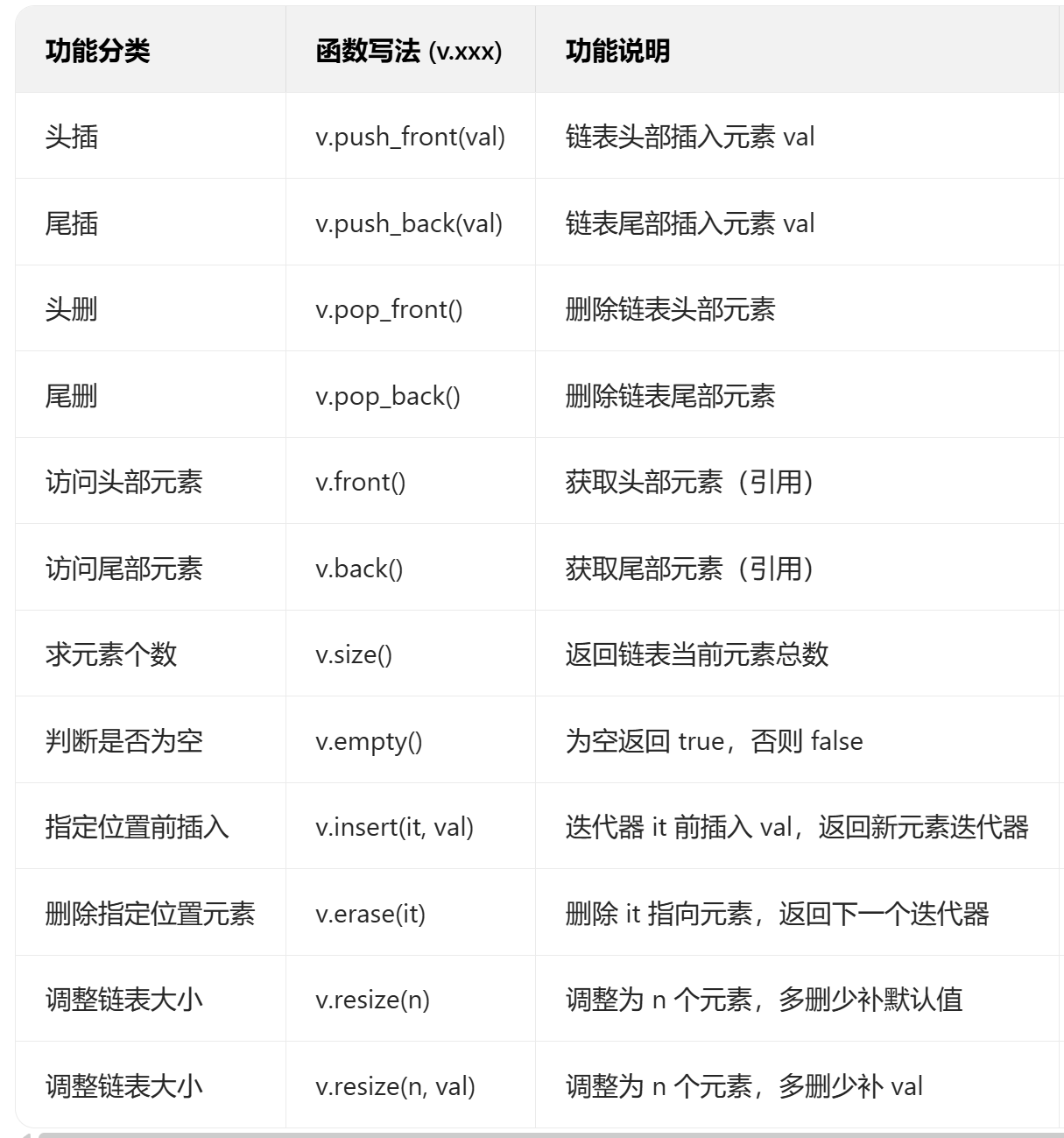
双向链表
接下来我们来学习下与单向链表相对应的------双向链表
这里我们也是要用数组来进行模拟实现:
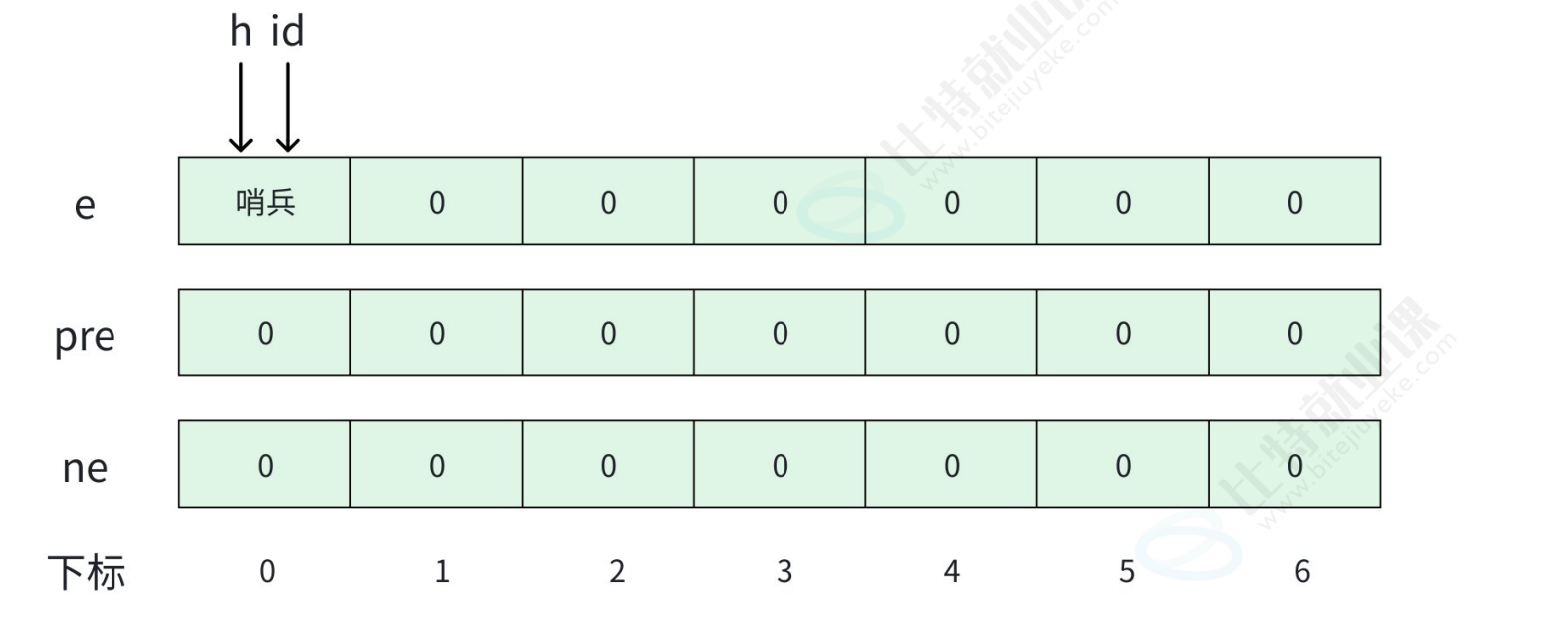
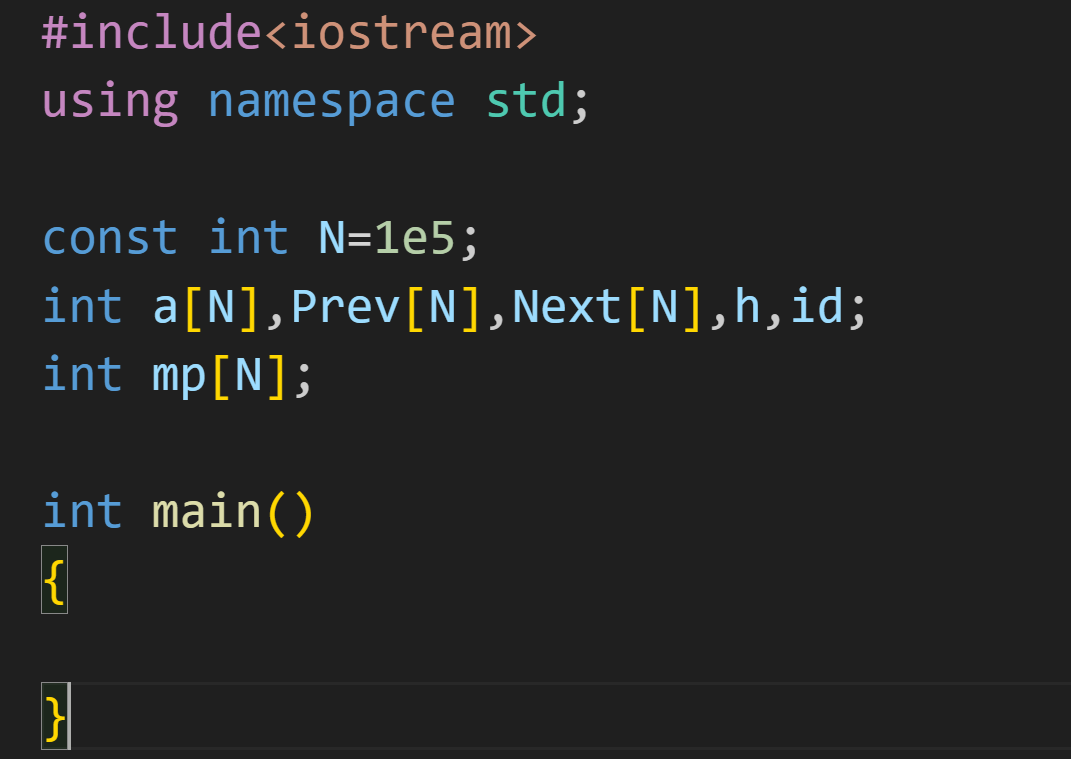
1.代码实现:
尾插

头插

查找

在指定位置后插入
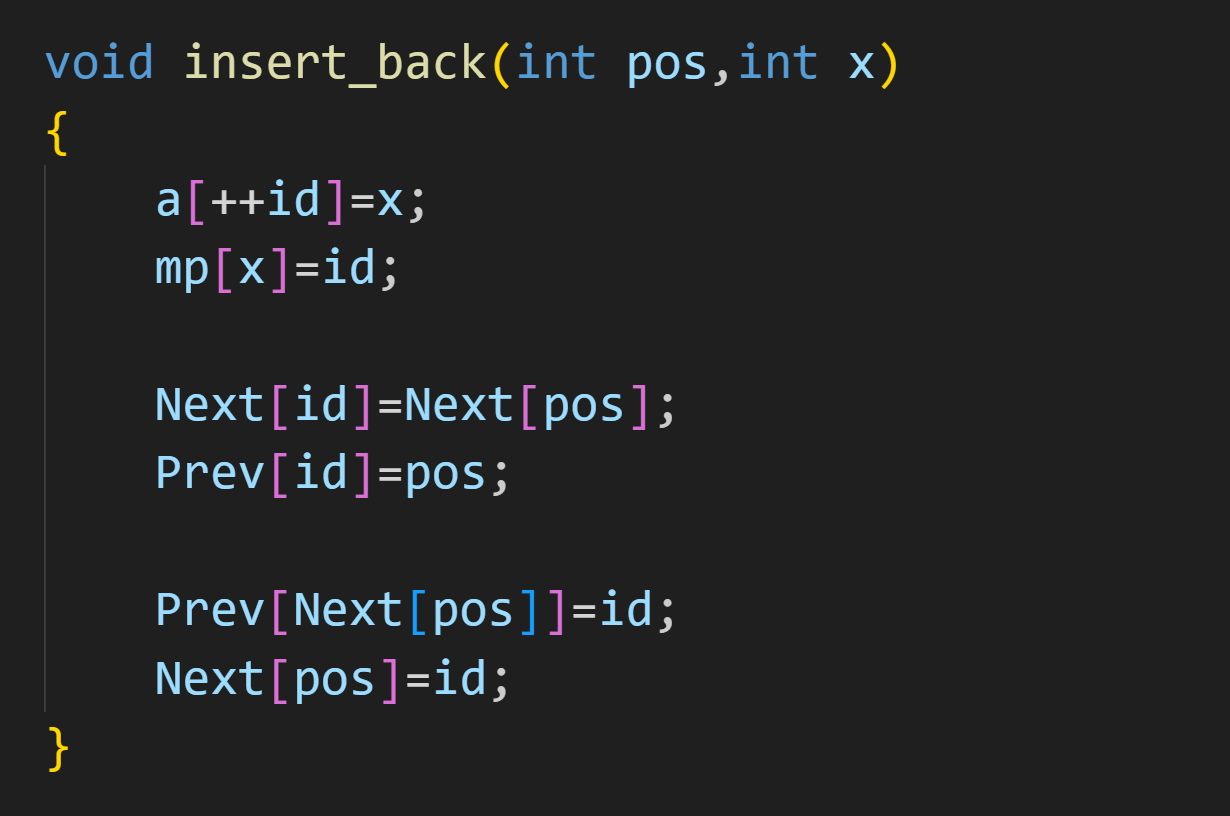
在指定位置前插入
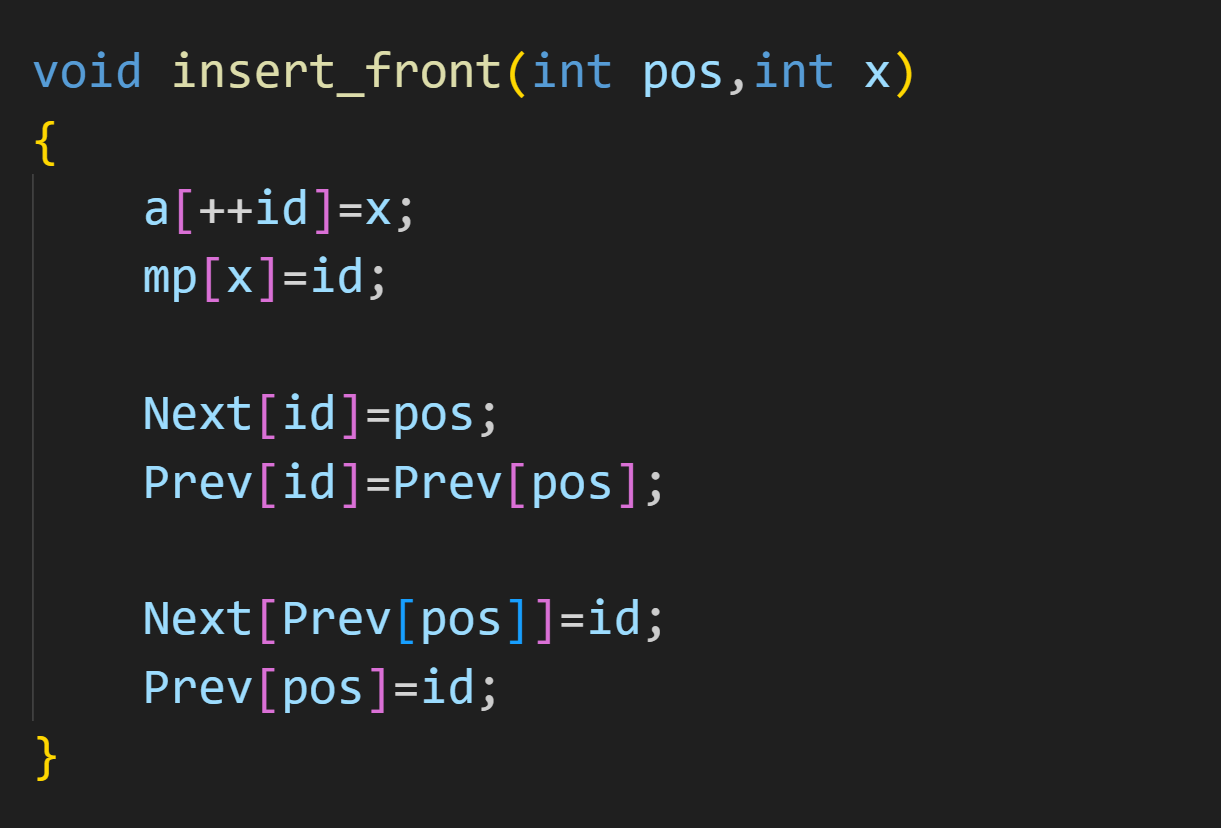
删除指定位置

打印

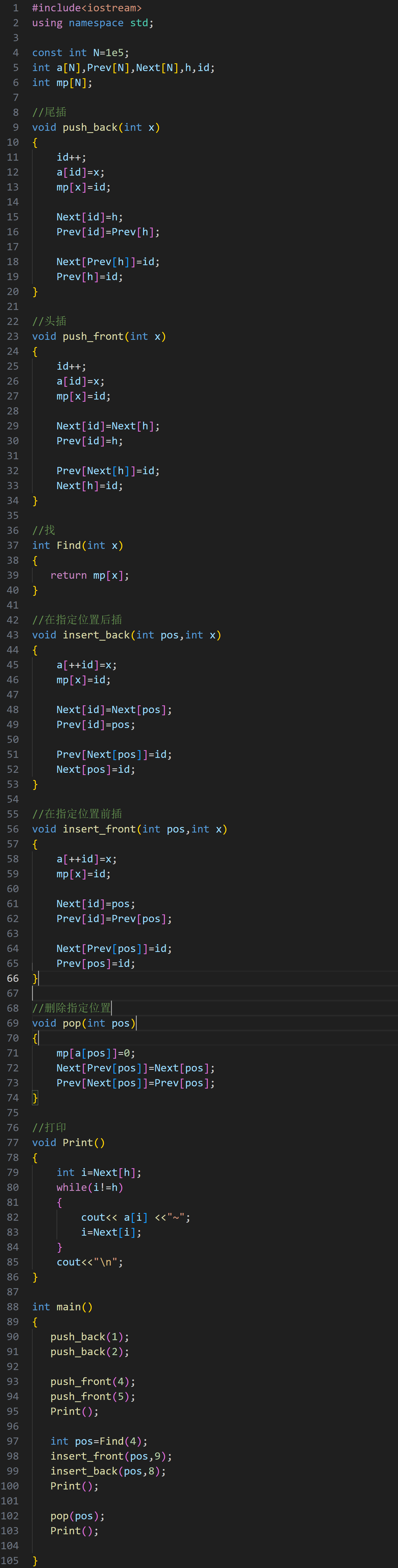
完整代码:
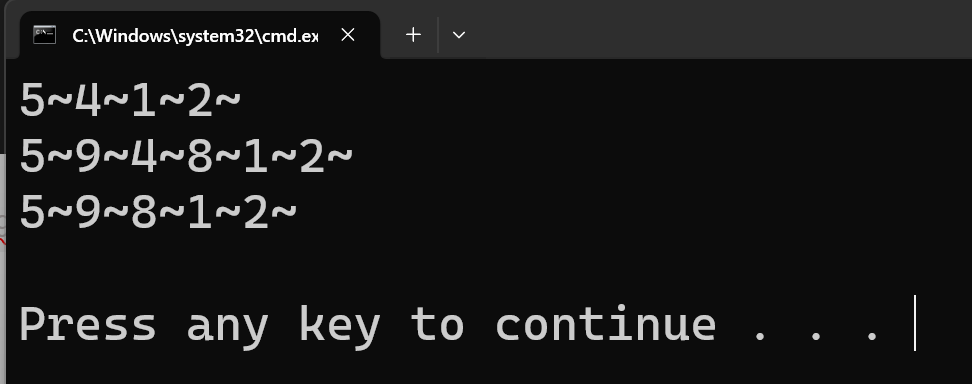
例题:
(1)排队顺序
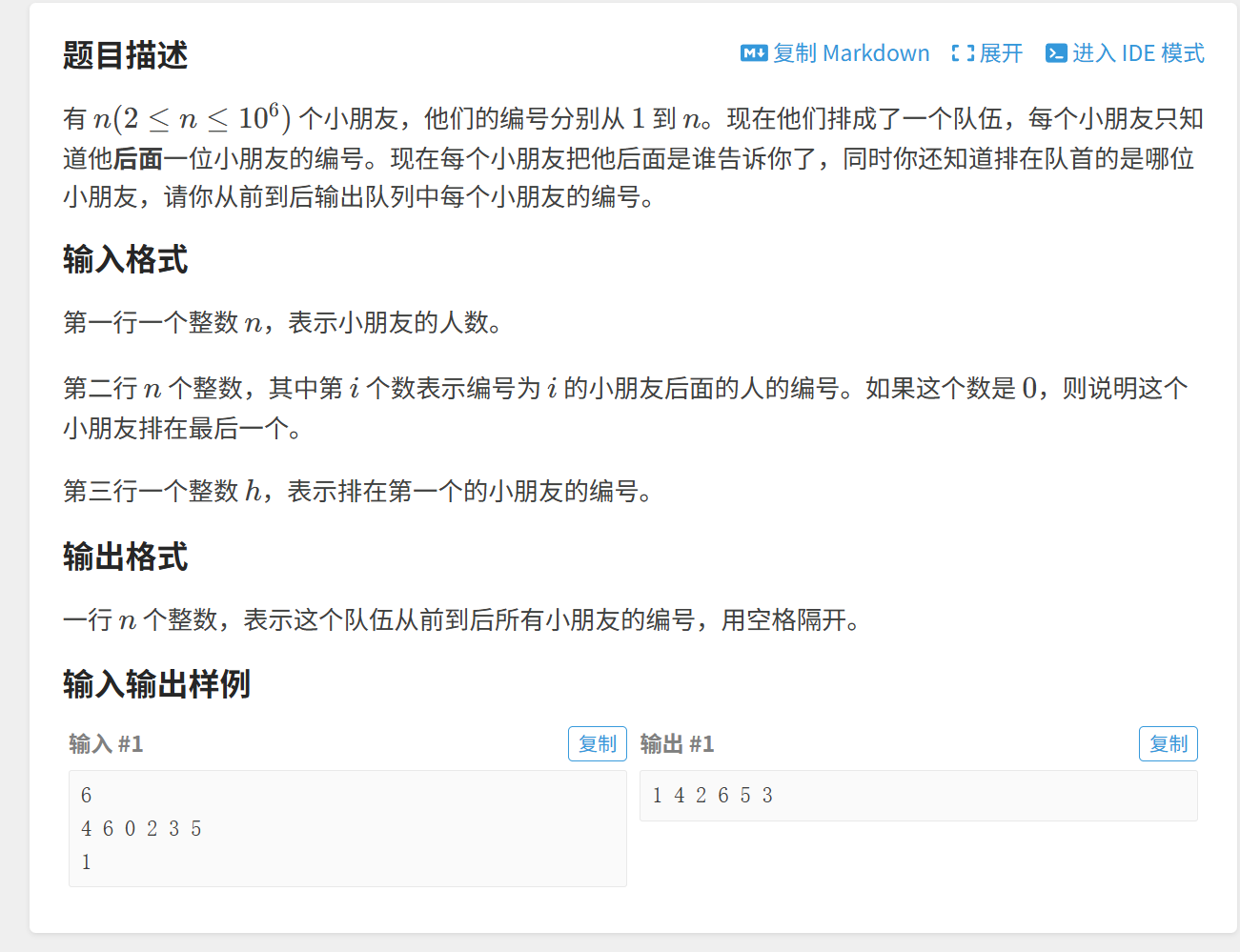
这道题就是很经典的链表题,直接展示代码:
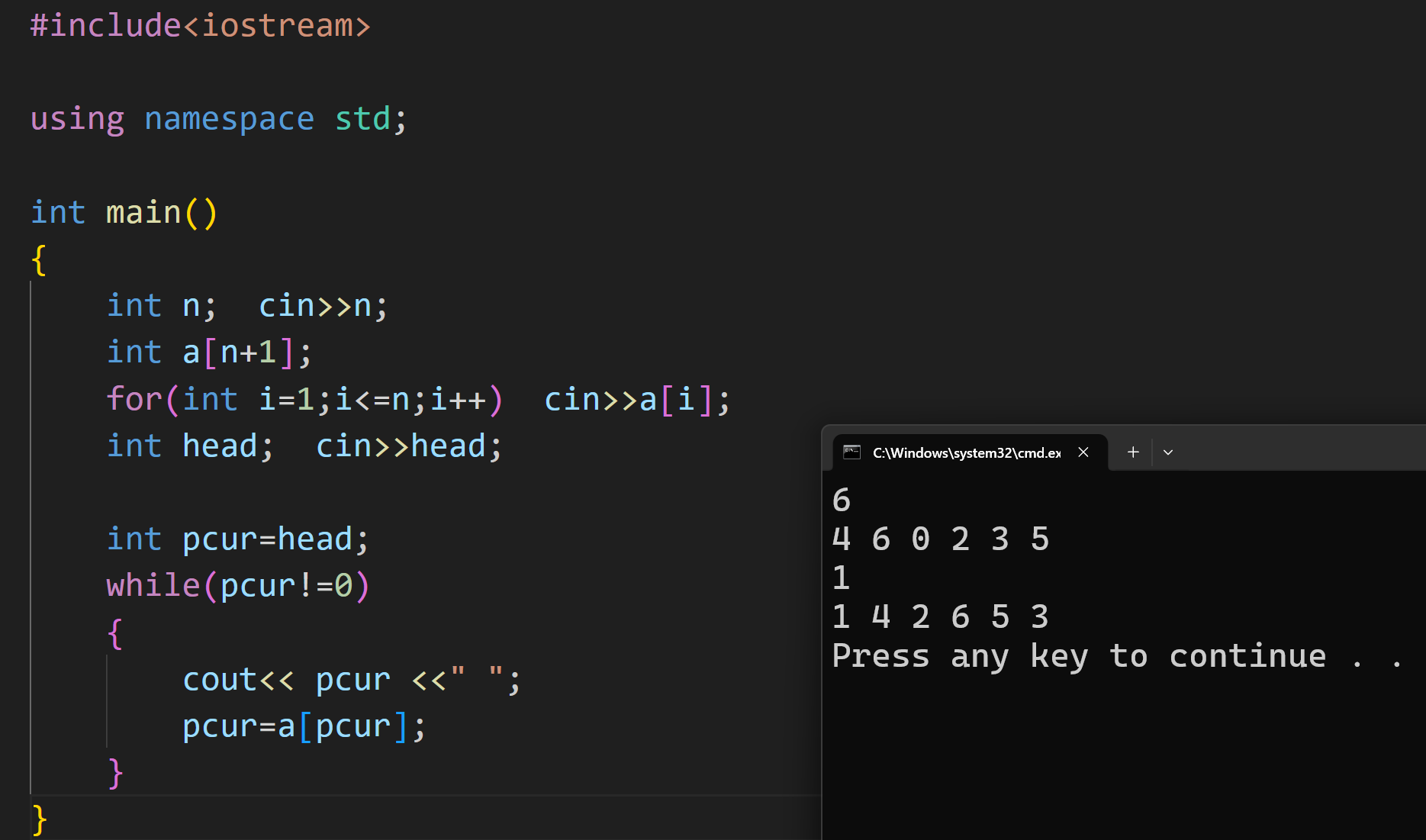
(2)队列安排

因为会在指定位置的左或右插入元素,我们可以用双向链表:
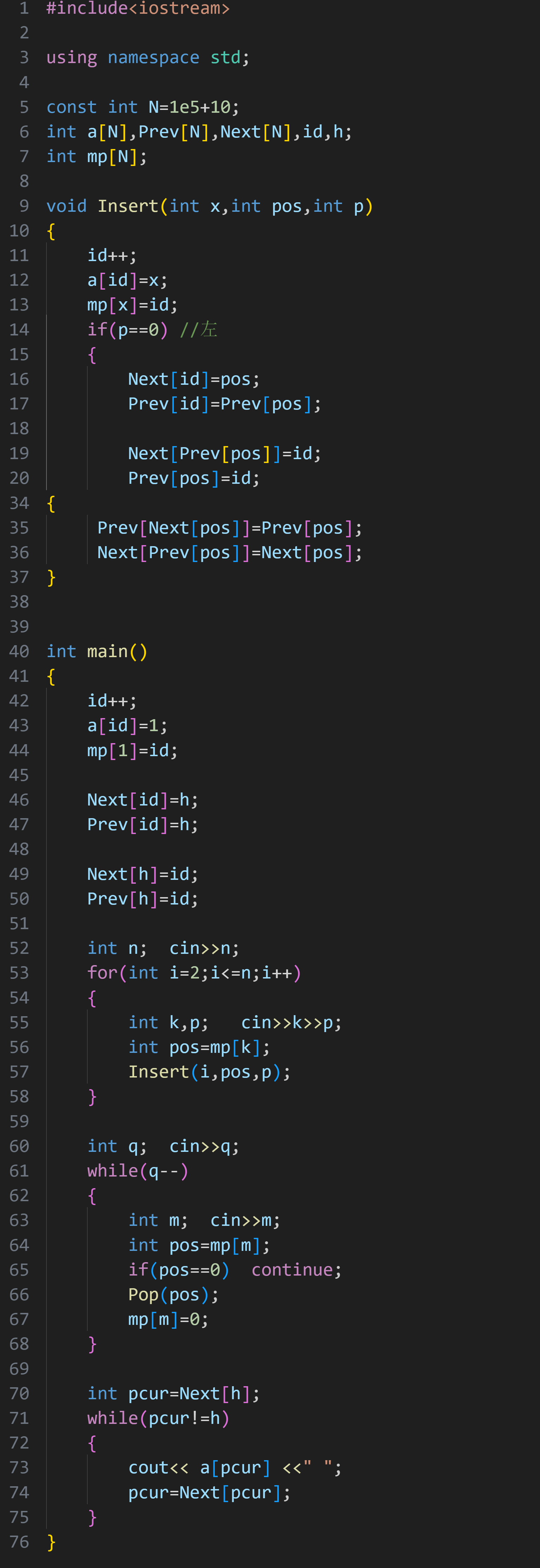
(3)约瑟夫问题
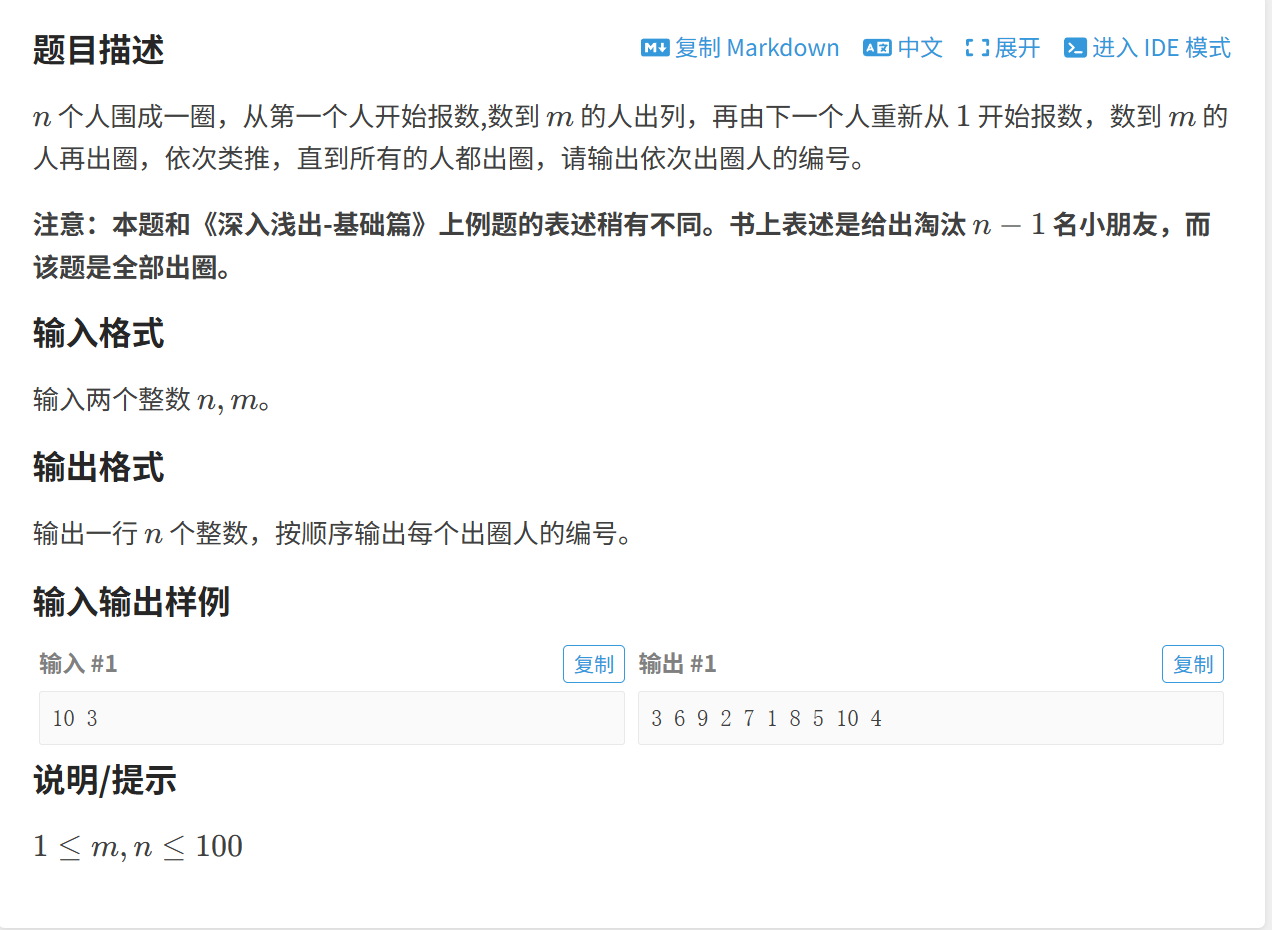
因为前面的模拟实现链表时,数组的初始值均为 0, 这就导致了,最后一个元素的 Next 指针域存的是 0 ,发现是指向哨兵位的,也就是说这是一个循环链表
这就非常适合解决约瑟夫问题
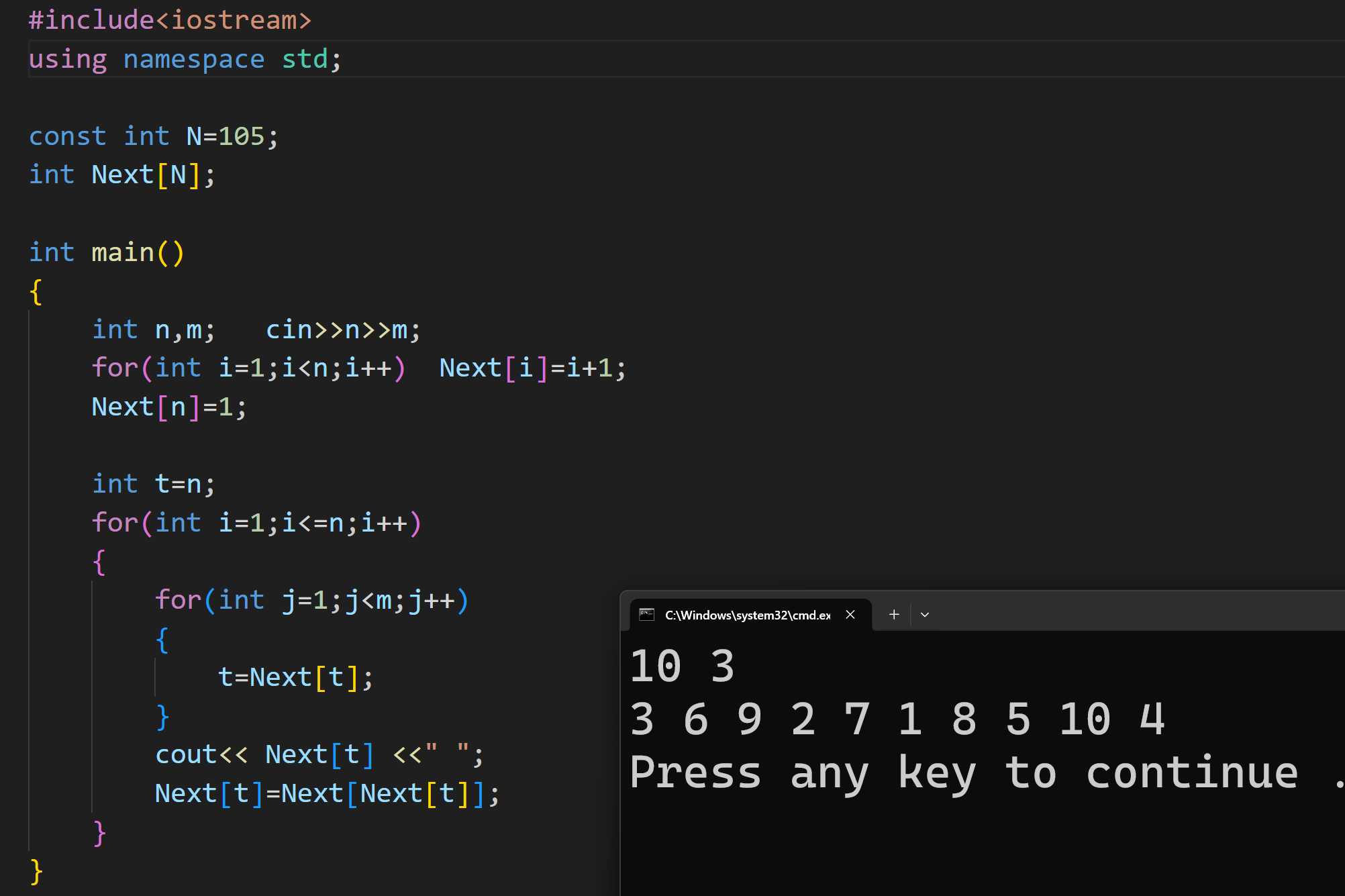
而解决这道题可以简化,只使用一个 Next 数组
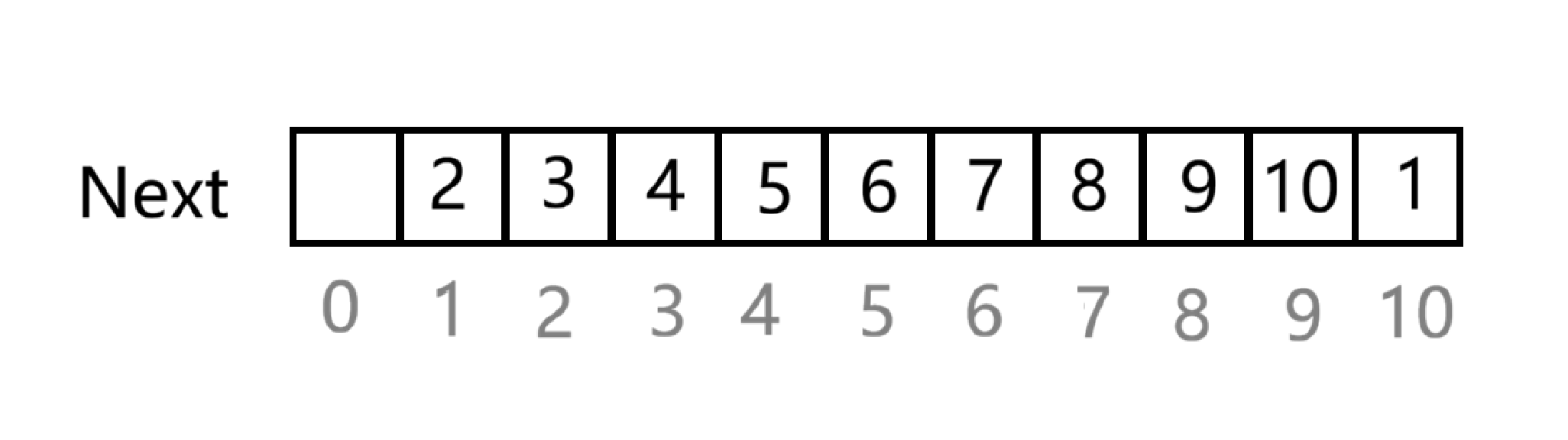
此时数组 1~10 的下标代表的就是 1~10 个数,对应位存储的是下一位的地址(下标),这样其实就是构建了一个循环链表

每次要找的是第 m-1 个数,也就是这一轮要出圈人的上一个人(找到上一个人这样好进行删除操作),我们先定义一个指针 t 来指向下标为 n 的这个位置(也就是第一个人的上一个)
因为最终每个人都会出圈,一共会进行 n 轮出圈操作,先来个 for 循环
在每一轮的出圈操作中,要从 1 开始计数,直到 m-1
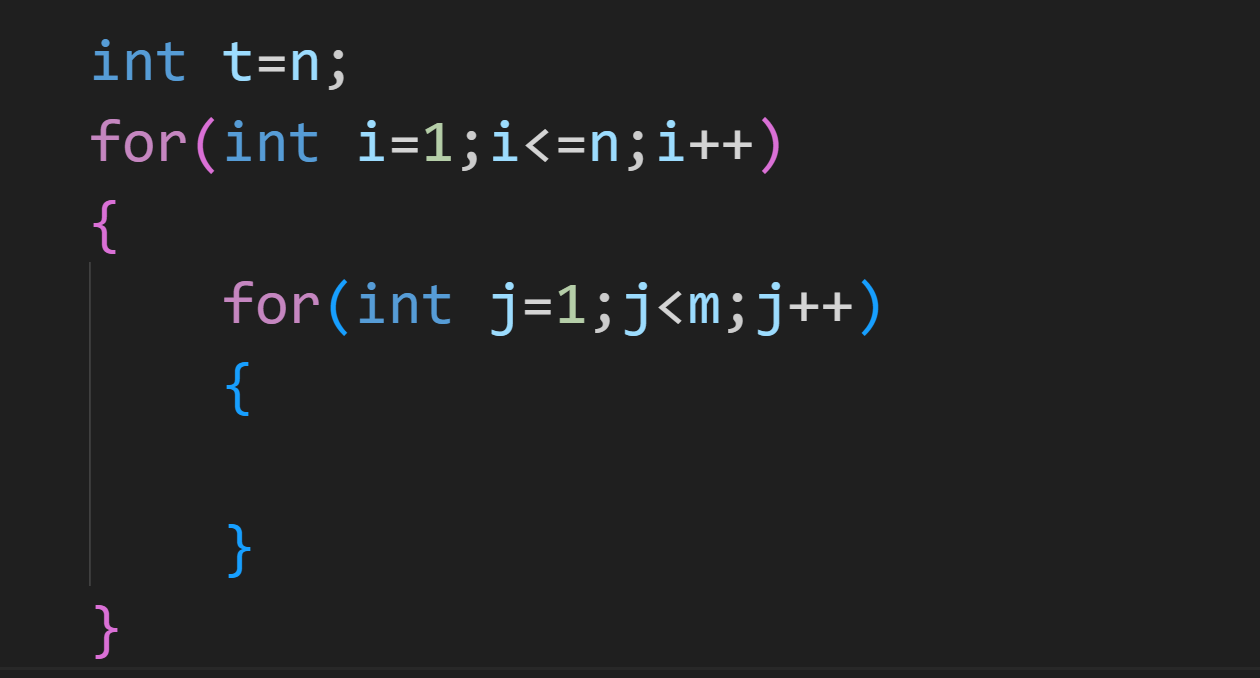
每一次要遍历这个链表,t=Next [ t ]
出了这层循环后,此时 t 指向的下一个位置就是本轮要出圈的,先将其打印,接着就是删除指定位置之后元素的操作
完整代码:
三.栈
栈是⼀种只允许在⼀端进⾏数据插⼊和删除操作的线性表
• 进⾏数据插⼊或删除的⼀端称为栈顶,另⼀端称为栈底。不含元素的栈称为空栈
• 进栈就是往栈中放⼊元素,出栈就是将元素弹出栈顶。
大白话讲:栈是一种访问受限的线性表,核心特点是后进先出
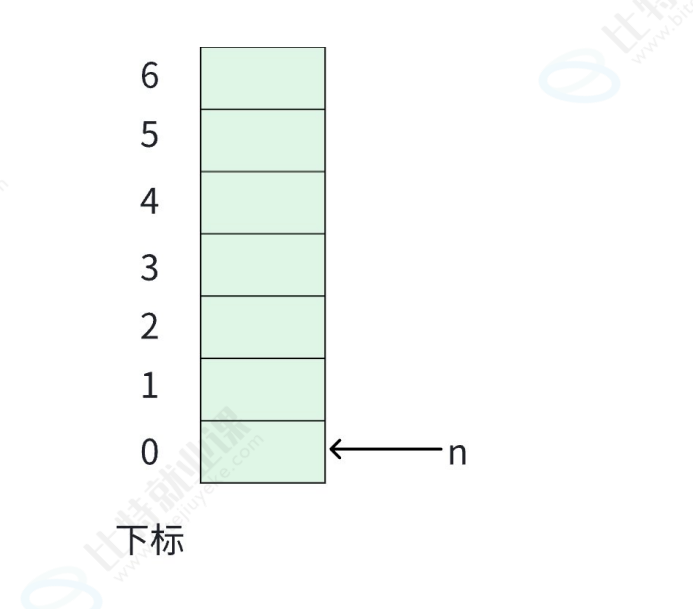
所以栈用数组模拟实现起来非常简单
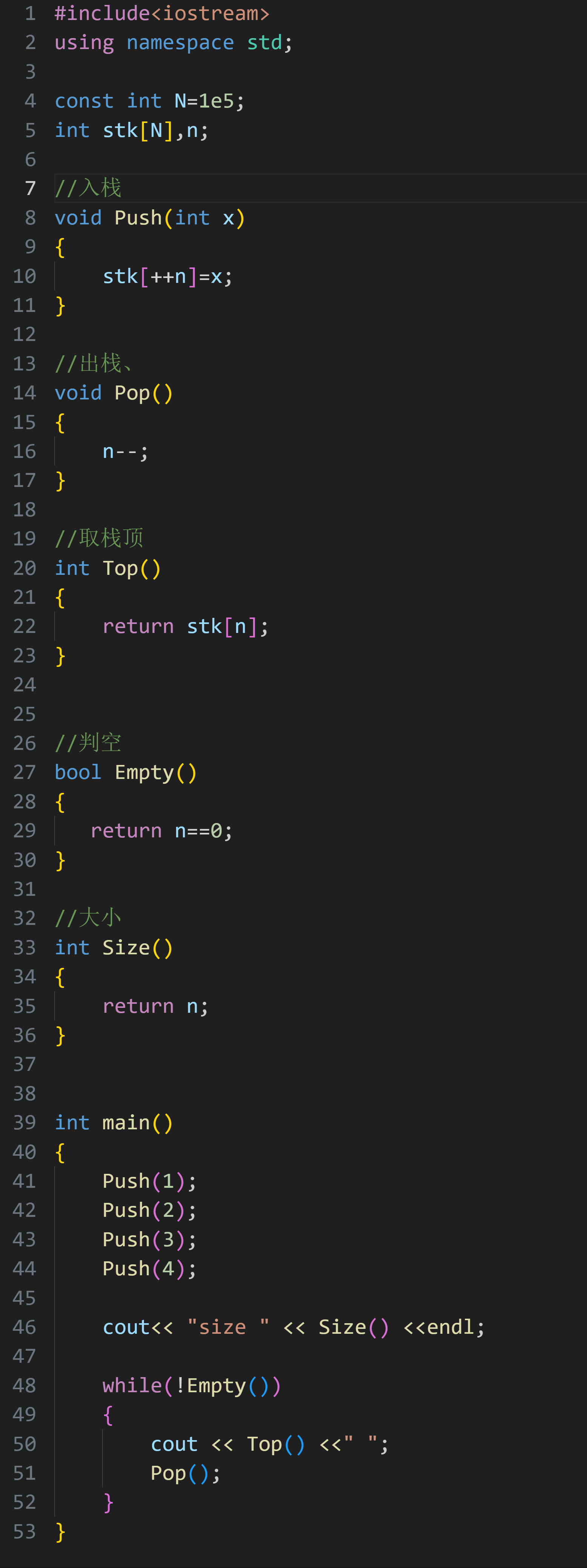
1.实现方式
入栈

出栈

返回栈顶元素

判空

栈的大小

完整代码:
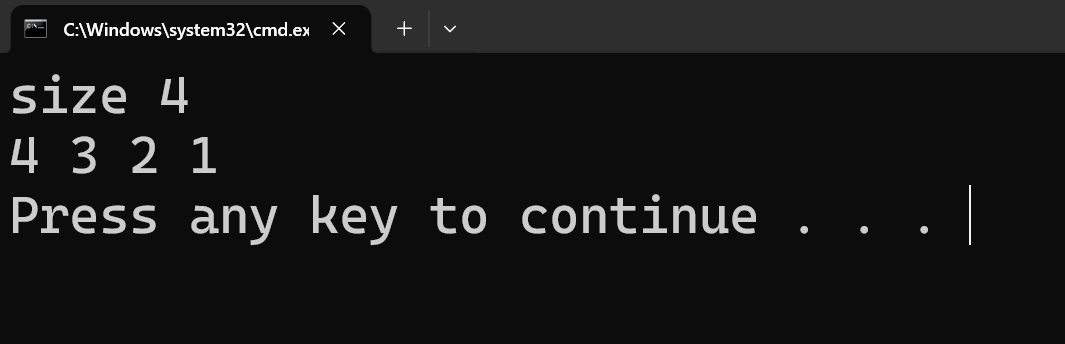
2.STL_stack
依旧是头文件

依旧大差不差的初始化

相关函数:
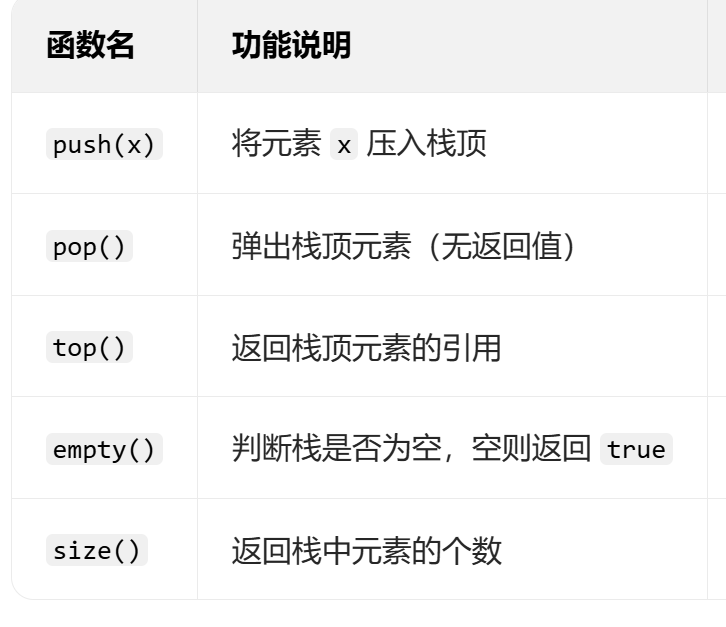
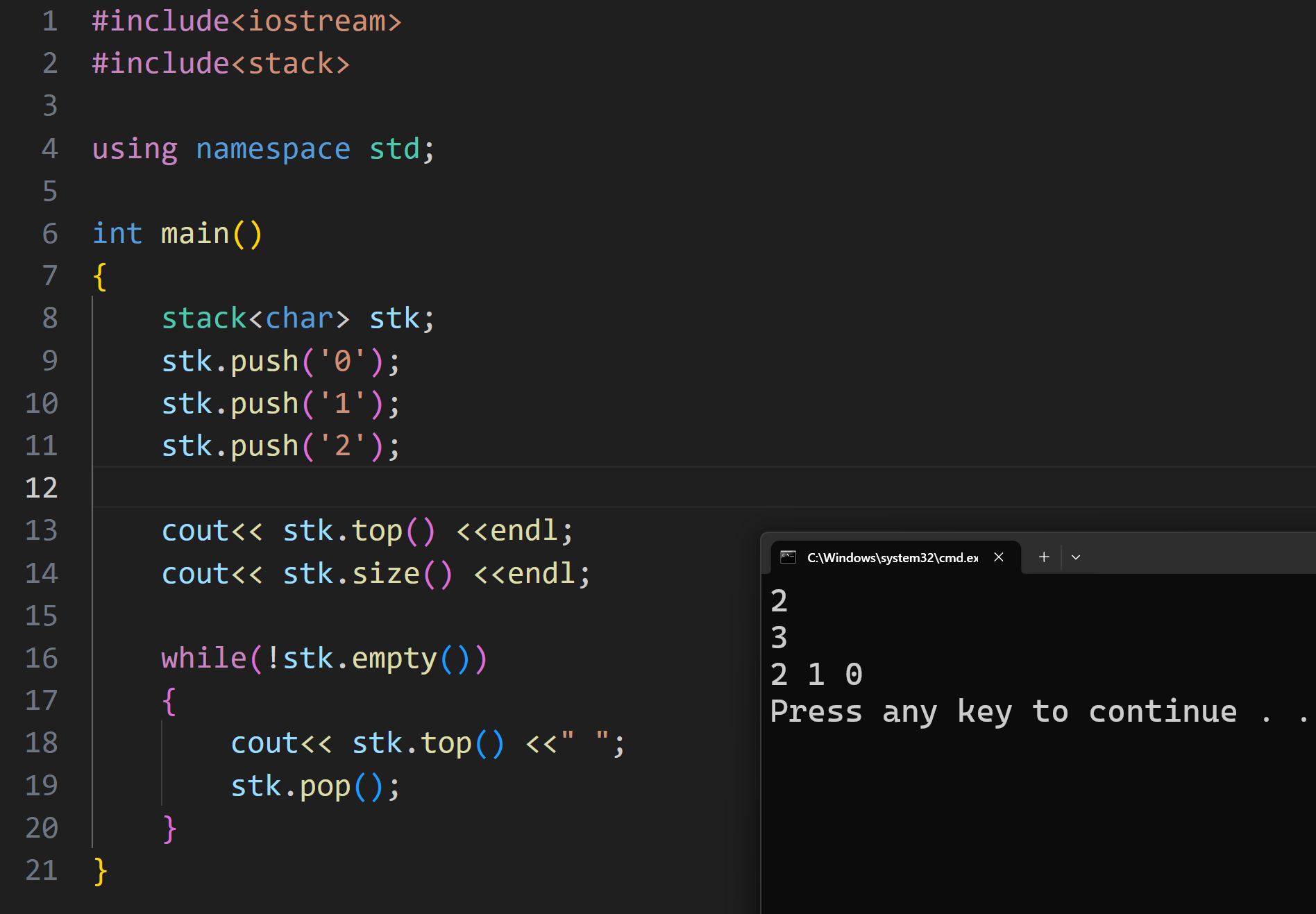
3.例题
(1)有效括号
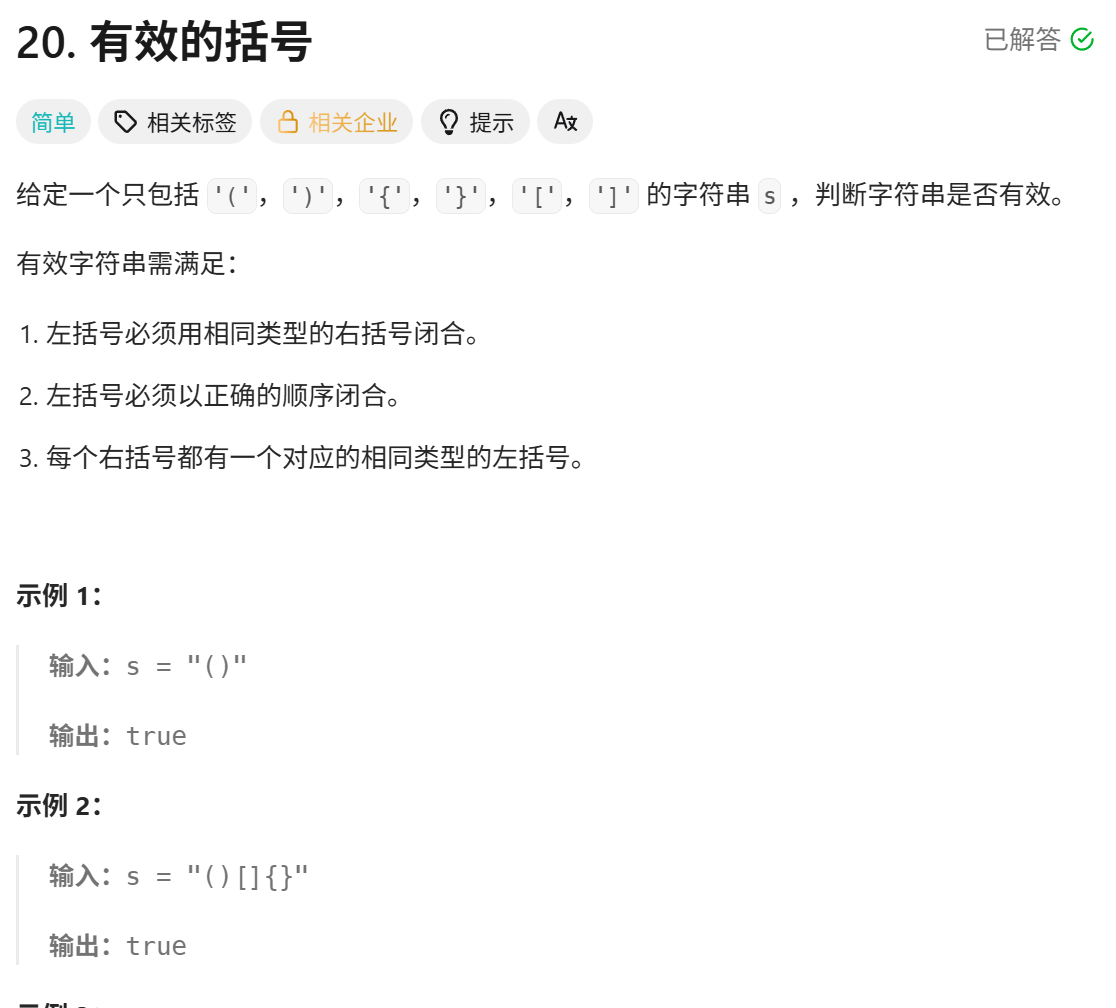
学习栈一定就会学习这个有效括号问题,思路就是,如果遇到左括号 "( " 、" { "、" [ "
就要进栈,如果遇到右括号 " )"、" } "、" ] ",就让其与栈顶元素进行比较,如果可以匹配就继续判断,如果不能就是 false
代码就很容易写了:
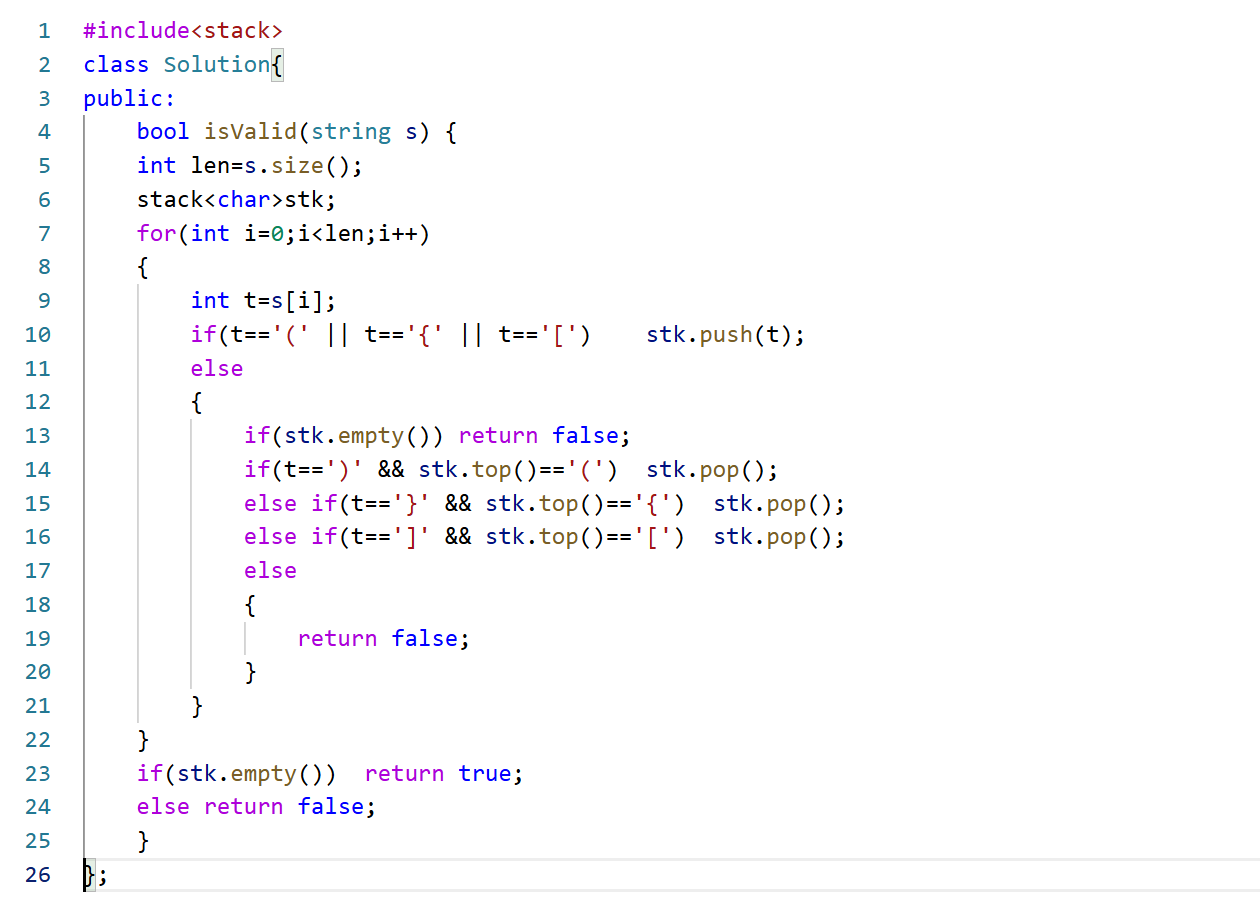
当然这里还有些细节,如果遇到右括号,但是此时栈为空,没有元素与此进行匹配,这时候也要 return false,以及当遍历完字符串后,如果此时栈中还有元素,也要return false
(2)验证栈序列

这道题的意思就是给定两段序列,第一段是入栈序列,判断第二段是否是其的出栈序列
要解决这个问题,我们要借助栈:
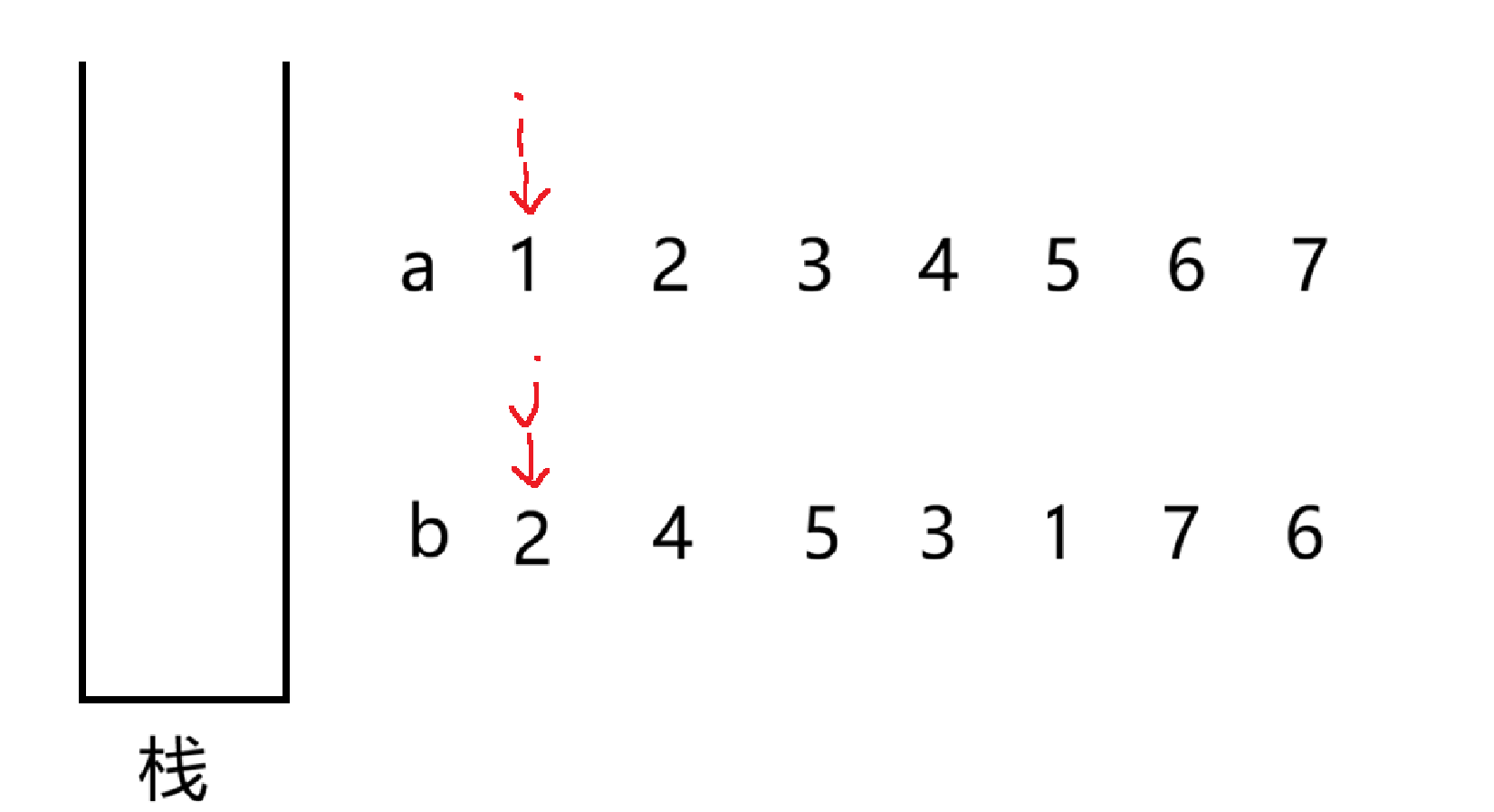
如上图,有 a , b 两个数组
大体思路,定义两个指针 i,j 分别指向两个数组的 "头",每一次将 a 数组中 i 指向的数入栈,接着判断 b 数组中 j 指向的数和栈里面的元素进行匹配,如果匹配失败,继续将 a 中的数入栈,如果相等匹配成功,先 pop 掉栈顶元素,接着就让 j++,循环判断,我们画图演示下
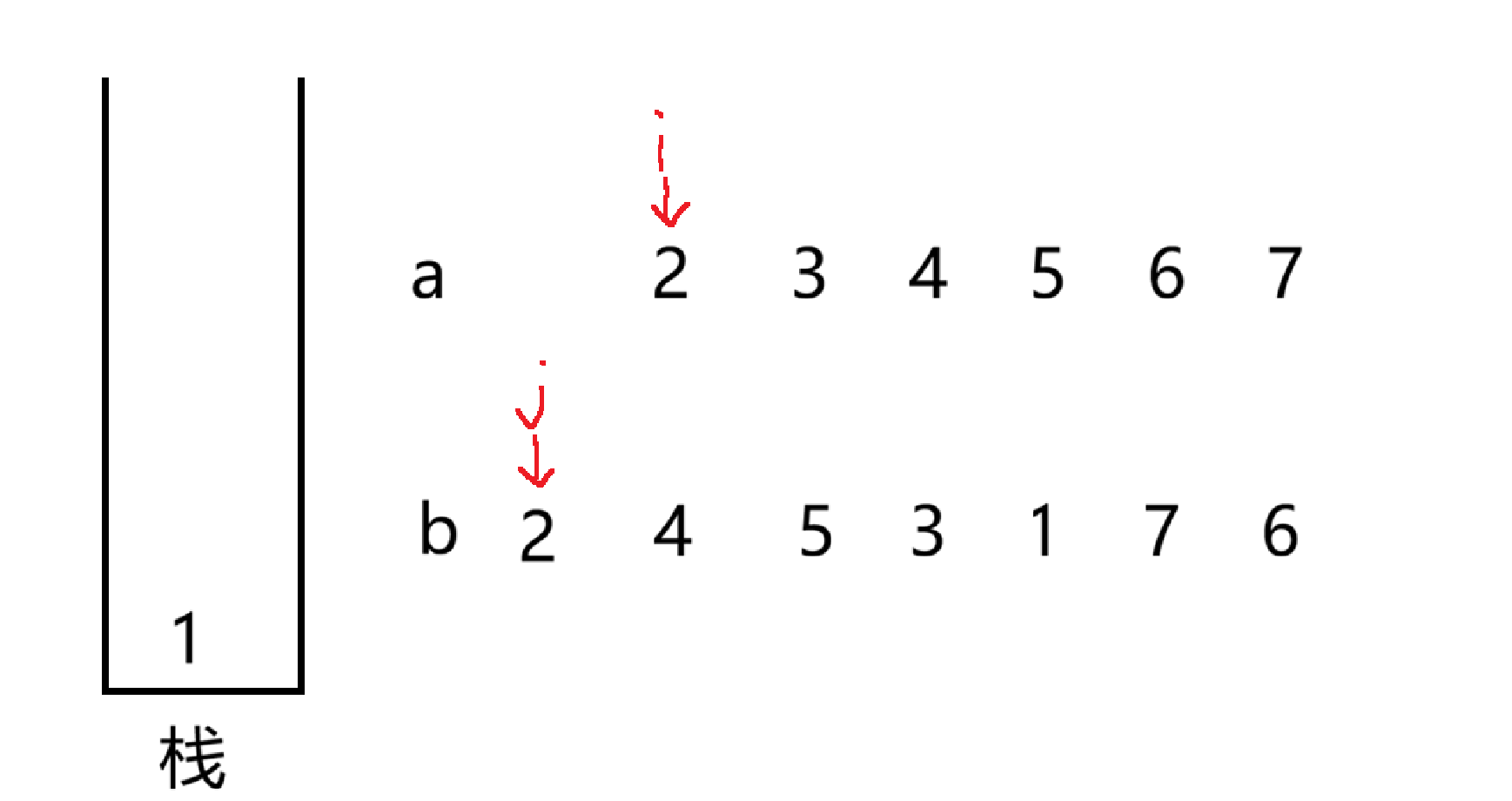
让 1 入栈,然后判断,发现 1 和 2 不相等,i++,继续入栈
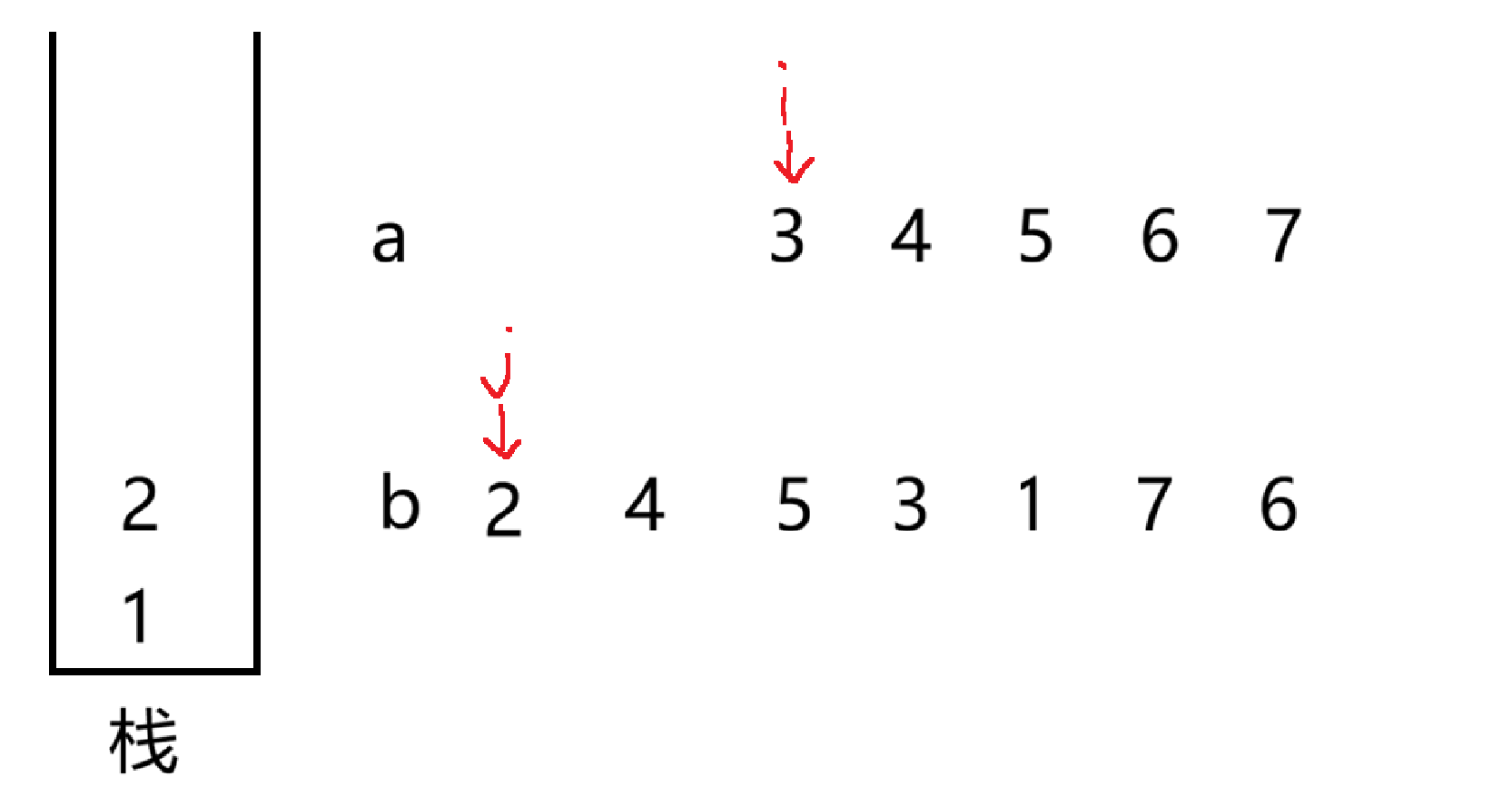
此时栈顶元素与 b 中 j 指向的数相等,就 pop 栈顶元素,接着 j++
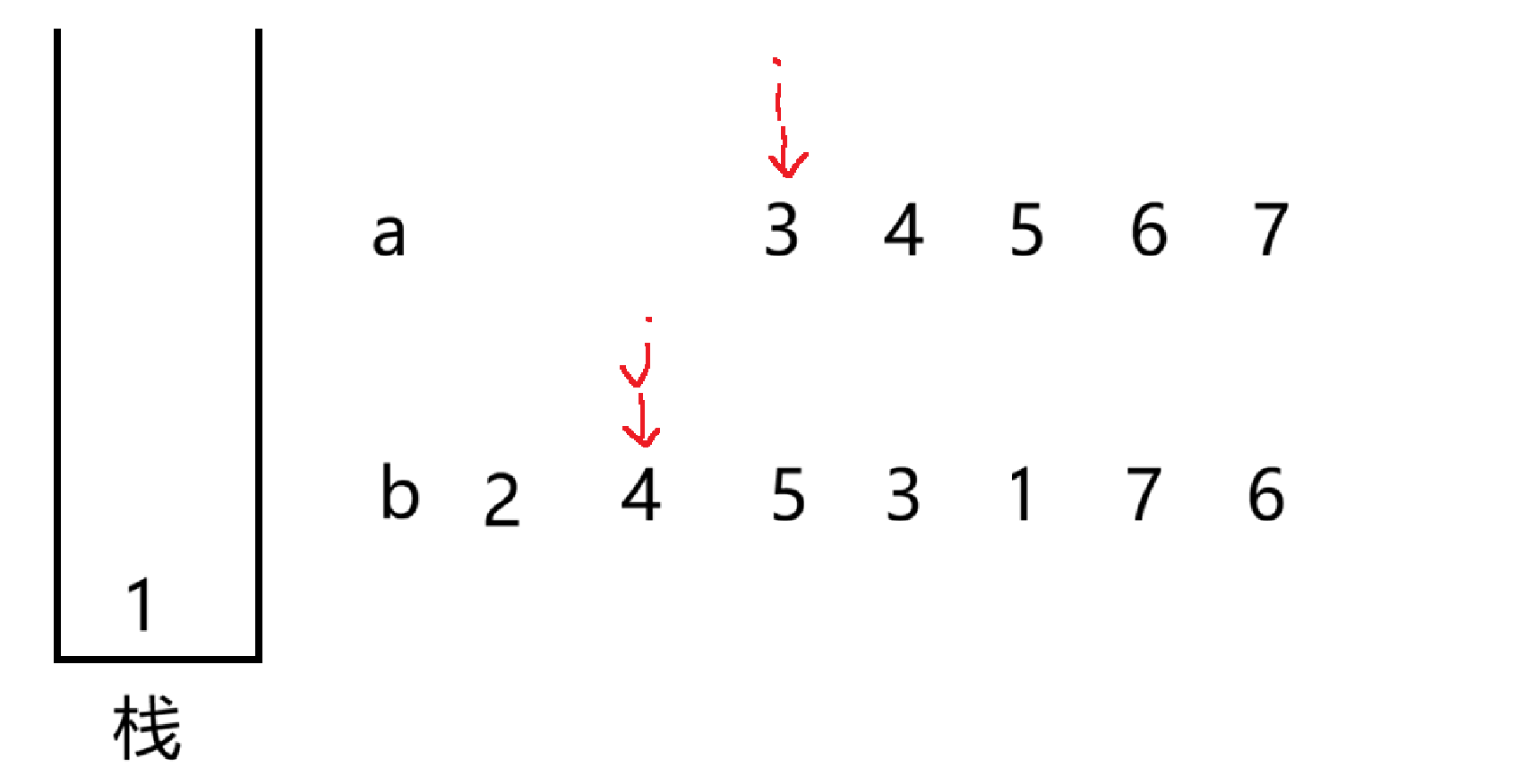
4 不等于栈顶元素 1,就继续让 i 指向的数入栈,不断重复此操作
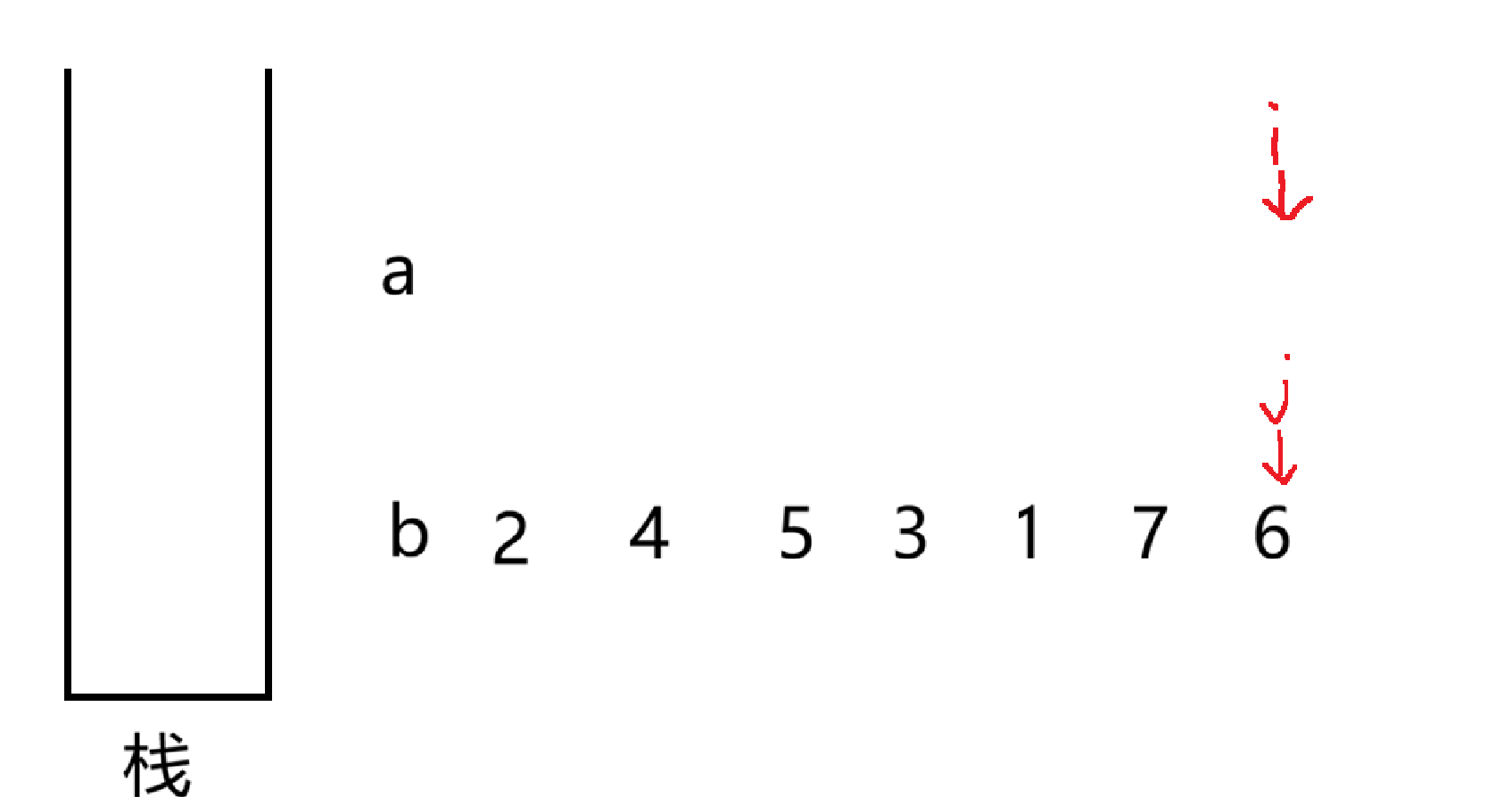
当 i 遍历完 a 数组,如果栈为空,就说明是可以以 b 数组的序列输出,就是 "yes"
下面是代码实现:
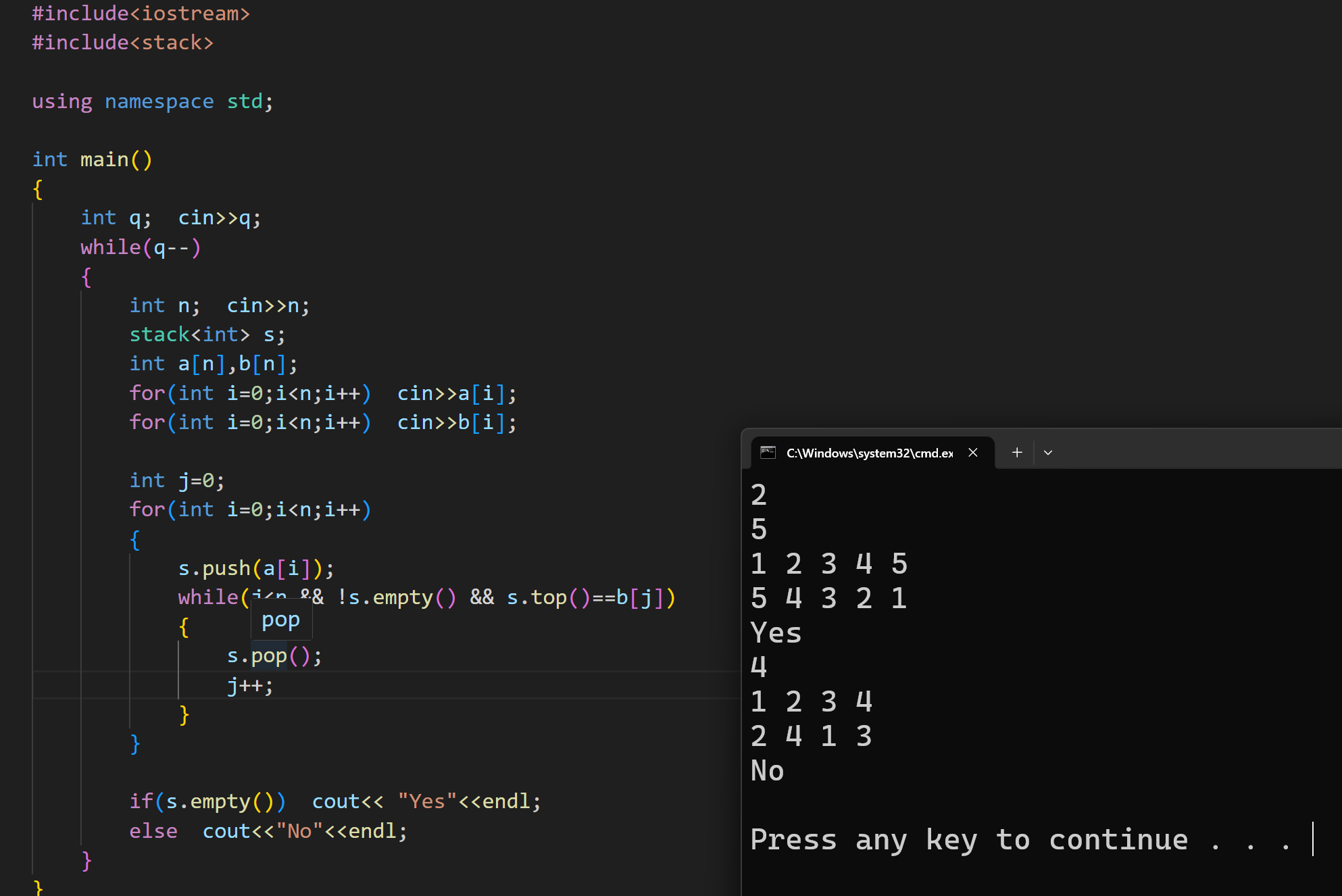
(3)后缀表达式
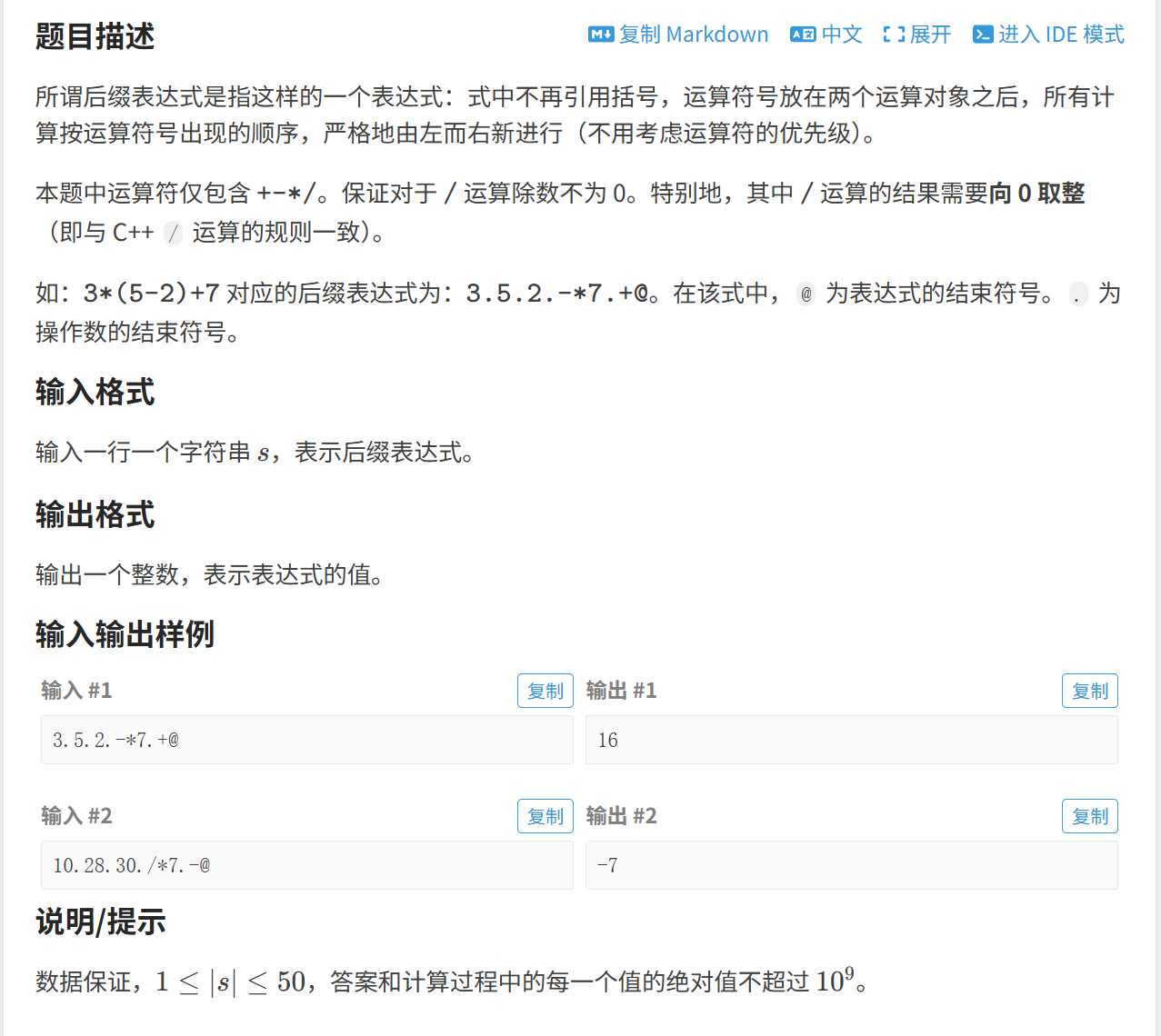
这道题意思其实很简单,数字之间会用 " . " 分隔开,当遇到运算符号时,就计算离其最近的两个数,将计算结果代替到原来的两个数,重复计算。
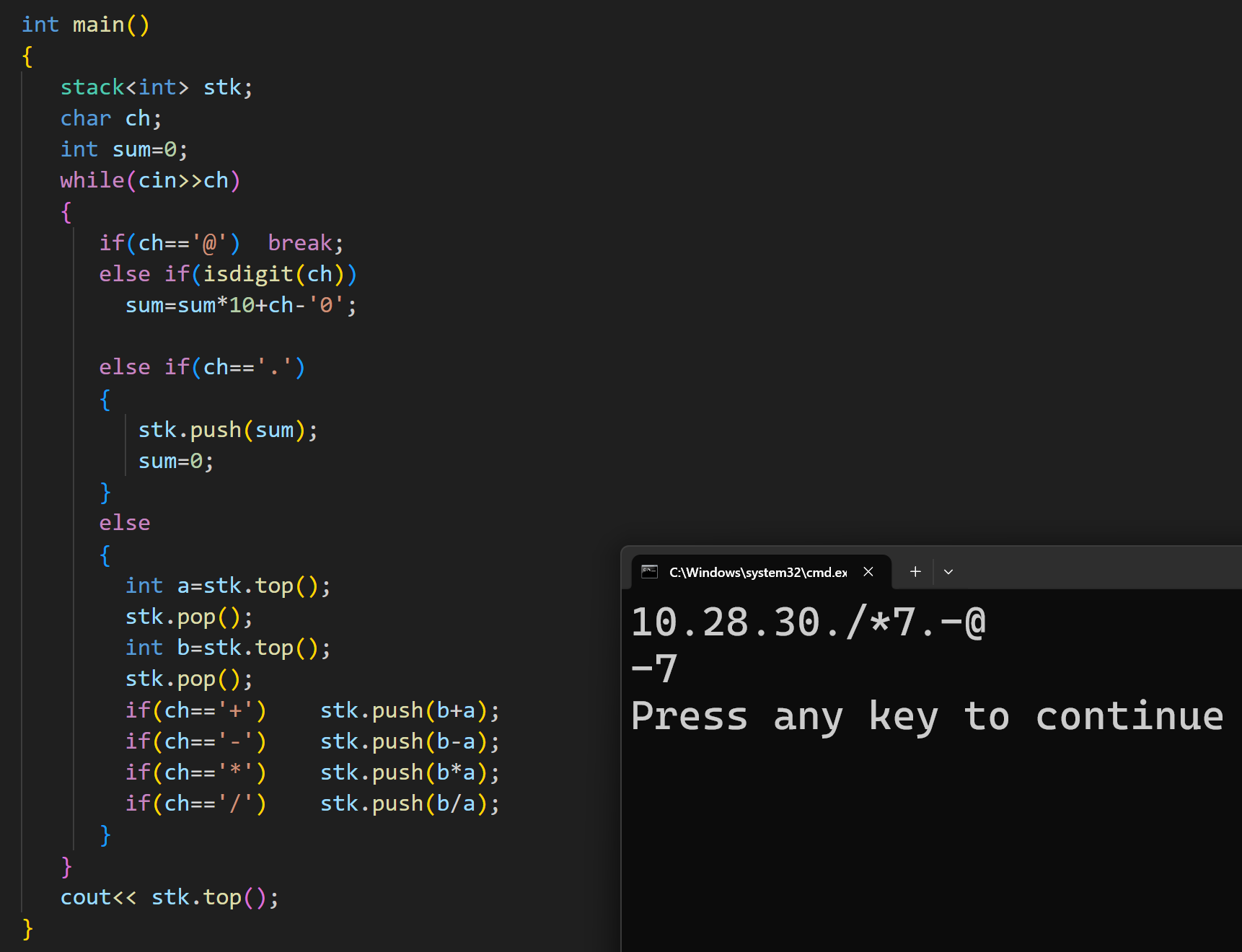
这也是用栈来解决,遇到数字就进行入栈操作,遇到运算符就拿两次栈顶的元素进行计算,然后将计算结果继续入栈
代码实现:
四.队列
队列也是⼀种访问受限的线性表
它只允许在表的⼀端进⾏插⼊操作,在另⼀端进⾏删除操作
• 允许插⼊的⼀端称为队尾,允许删除的⼀端称为队头。
• 先进⼊队列的元素会先出队,故队列具有先进先出(First In First Out)的特性
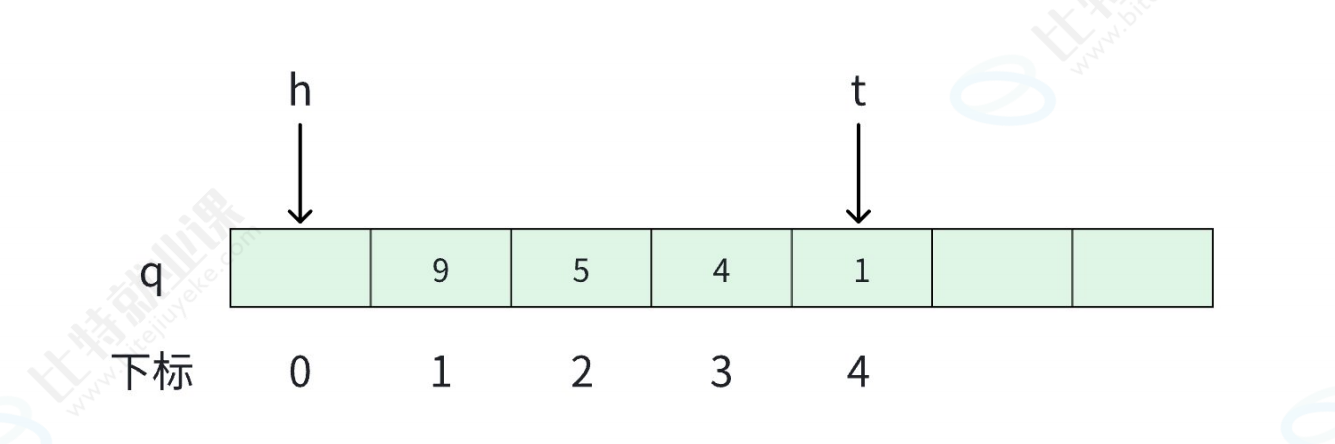
1.实现方式
用数组模拟队列也是很简单的,直接展示代码:
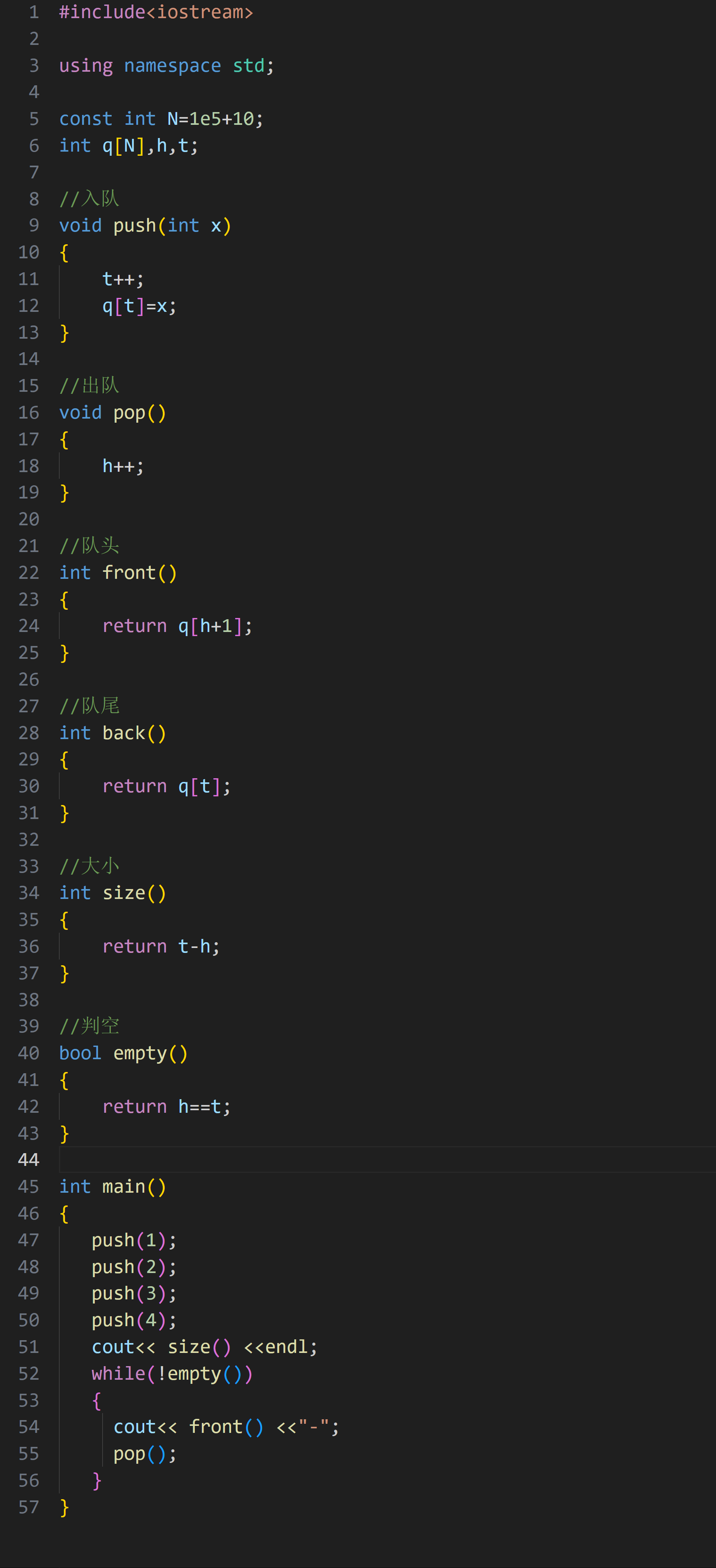

2.STL_queue
头文件:

初始化:

相关函数:
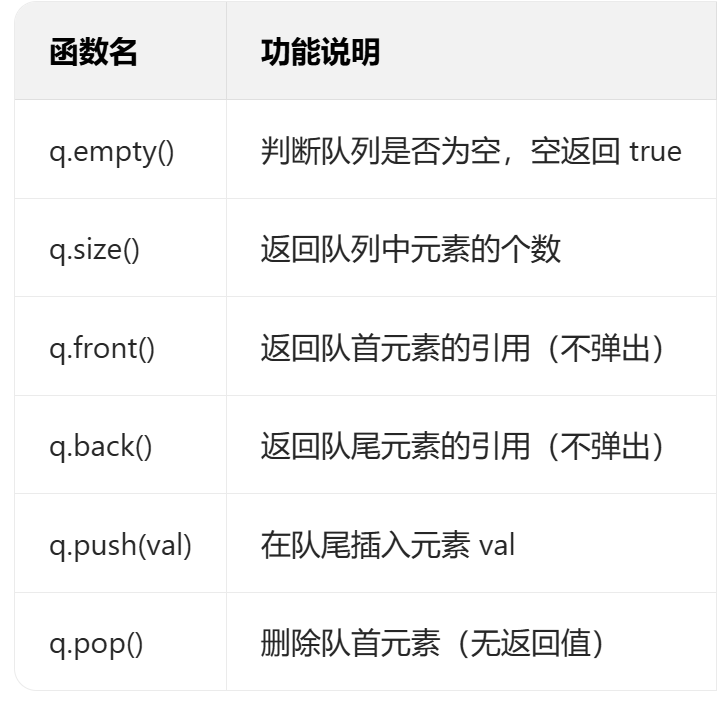
3.例题
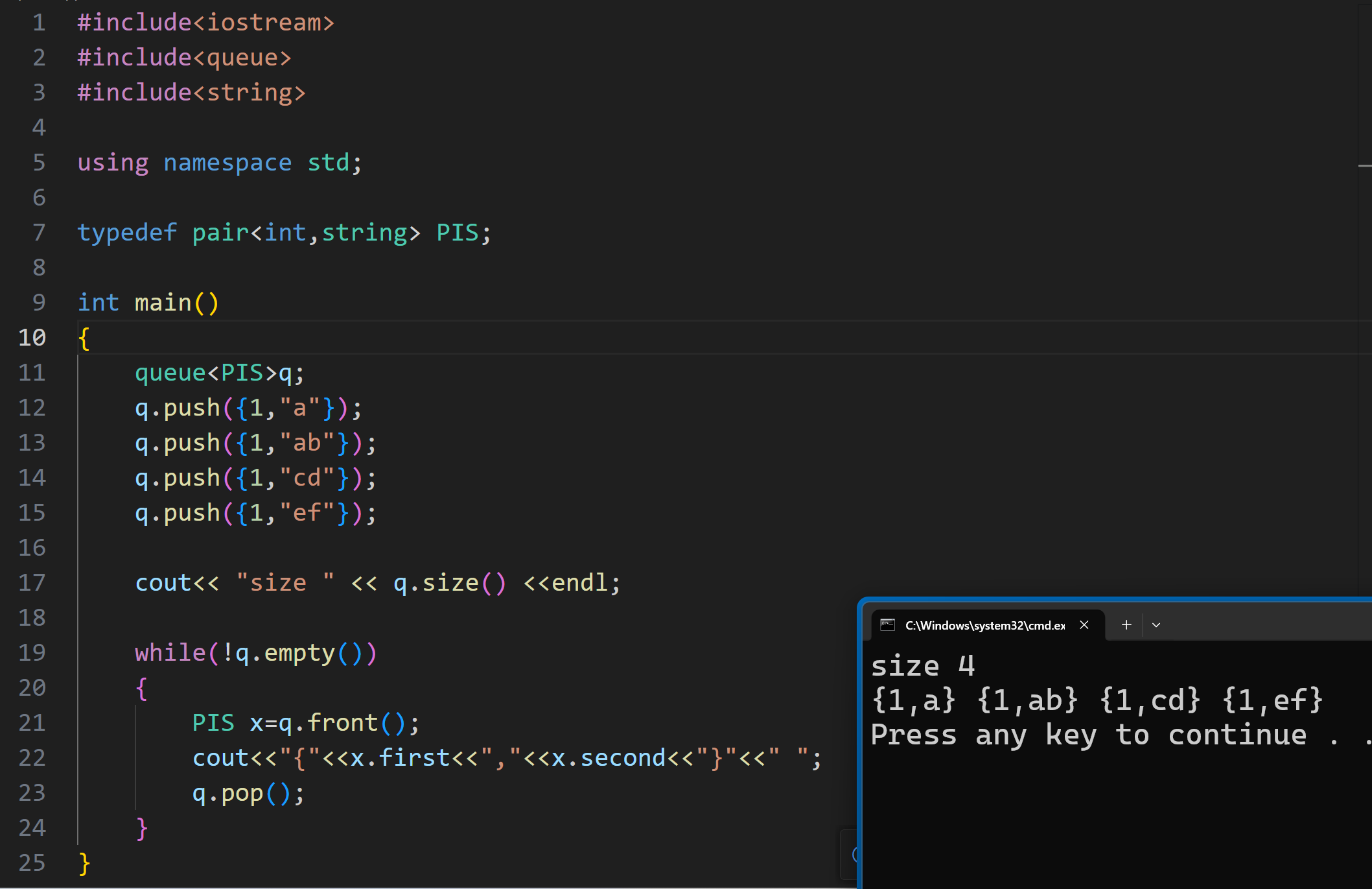
(1)队列

就是基本的队列模拟,直接上代码:
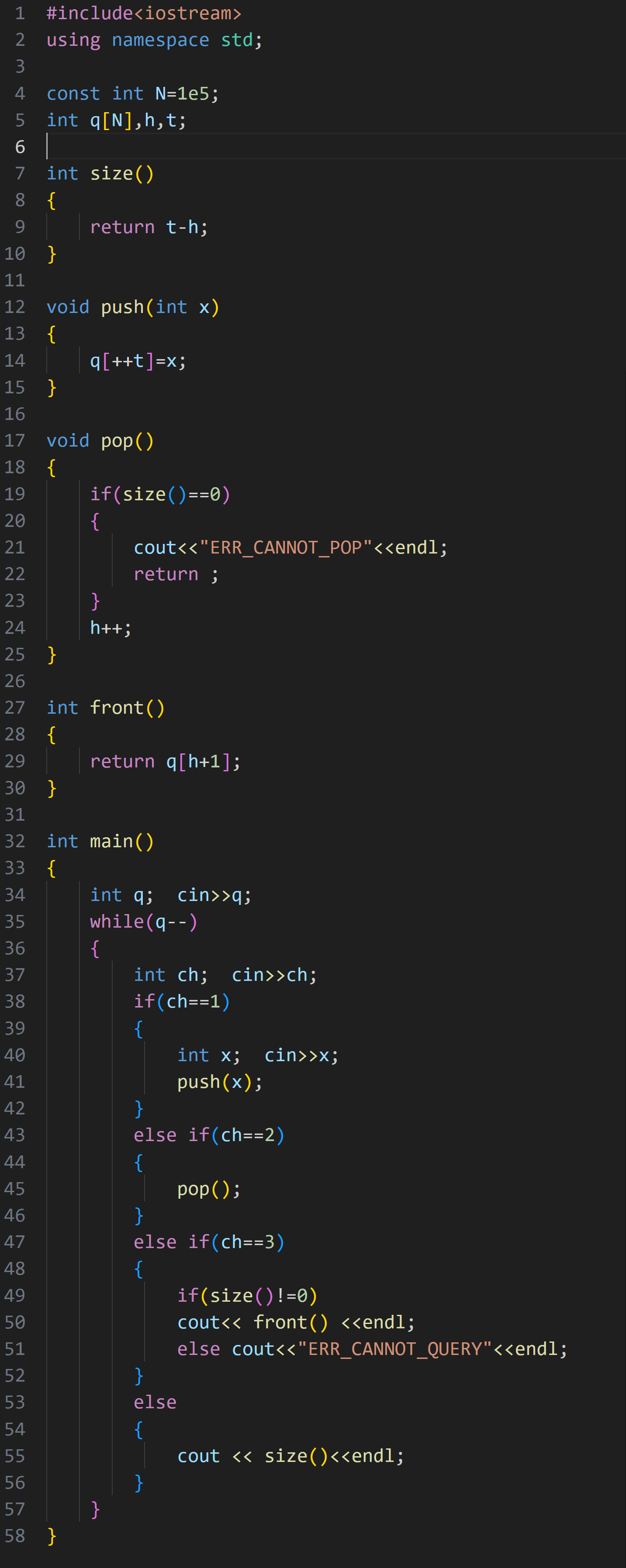
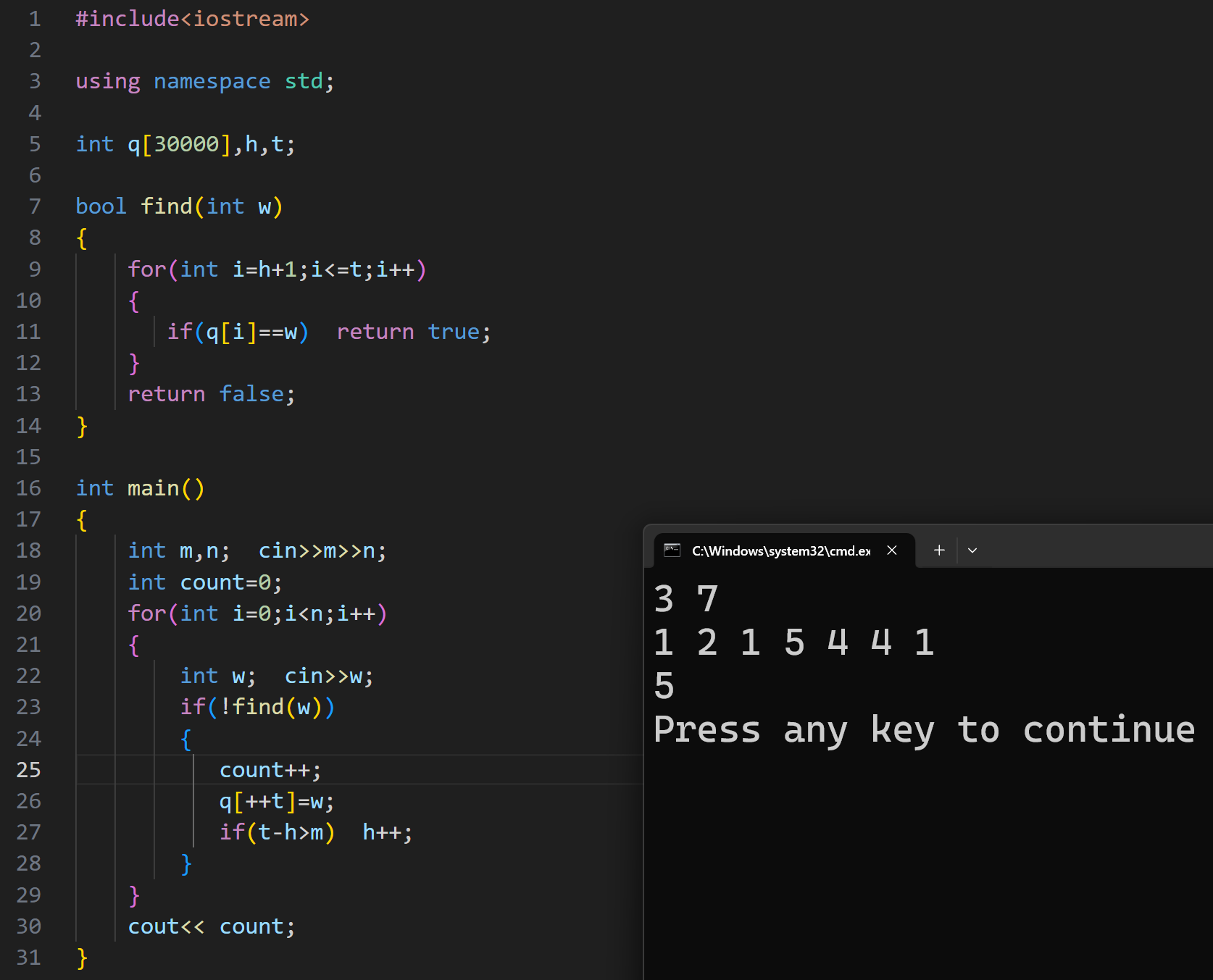
(2)机器翻译

这道题这么长,简单来说就是,有一个长度仅为 m 的队列,每次查询一个数,如果这个数不存在于这段队列,就进行入队,但注意要维护队列长度始终 <= m
直接上代码:
(3)海港

根据题意,我们要统计出 24 小时之内国籍的种数,因为是一段区间,如果新来船的时间减一开始的时间大于 86400s ,就要收缩统计区间
这里我们可以使用 pair ,队列中存放的类型为 pair<int ,int> ,第一个存到达的时间,第二个存国籍,因为要动态的管理 24h 内国籍种数,不可能每一次更新时间我们都要去重新计算一下
就得使用一个 mp 数组,和一个记录种数的 kind 变量
每一次将国籍存到 mp 里,当 mp 值为 0 ,kind++
如果进行收缩时间时,此国籍对应的 mp 值为 1 是,kind--
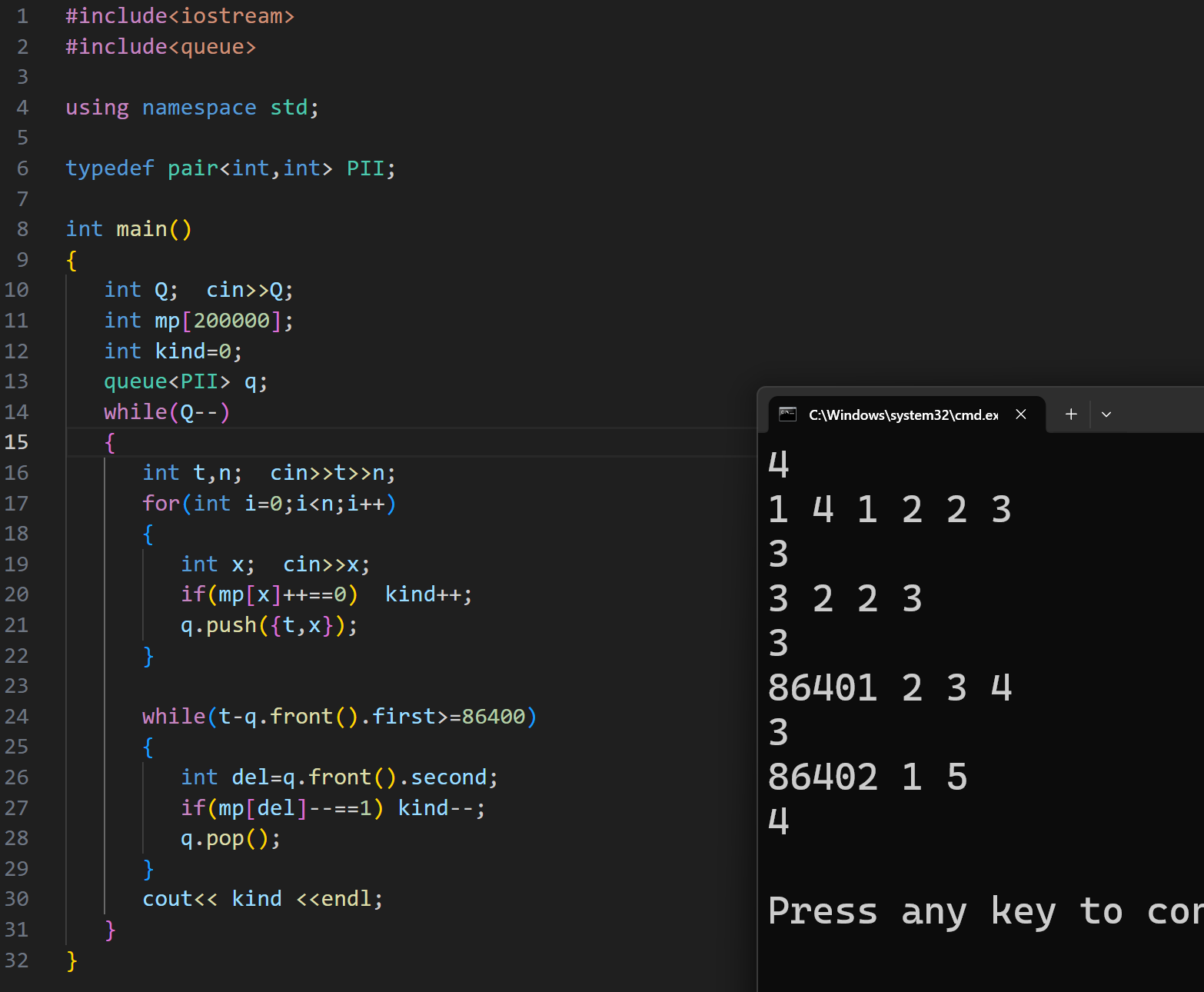
代码实现:
结语:
ok了,这一期关于算法竞赛中的数据结构就到这里了,制作不易,内容较长,可以点歌收藏,如果对你的学习有所帮助,关注我,我们一起学习进步
往期博客:
2.手撕二叉树