目录
[1.1 栈的核心概念](#1.1 栈的核心概念)
[1.2 Java中的Stack类](#1.2 Java中的Stack类)
[1.2.1 Stack类的基本使用](#1.2.1 Stack类的基本使用)
[1.2.2 Stack的继承关系(重要补充)](#1.2.2 Stack的继承关系(重要补充))
[1.3 栈的模拟实现](#1.3 栈的模拟实现)
[1.3.1 基于数组的实现(顺序栈)](#1.3.1 基于数组的实现(顺序栈))
[1.3.2 基于链表的实现(链式栈)](#1.3.2 基于链表的实现(链式栈))
[1.4 栈的应用场景(详细扩展)](#1.4 栈的应用场景(详细扩展))
[1.4.1 括号匹配校验器](#1.4.1 括号匹配校验器)
[1.4.2 浏览器前进后退功能](#1.4.2 浏览器前进后退功能)
[1.4.3 表达式求值(逆波兰表达式)](#1.4.3 表达式求值(逆波兰表达式))
[1.5 重要概念区分](#1.5 重要概念区分)
[2.1 队列的核心概念](#2.1 队列的核心概念)
[2.2 Java中的Queue接口](#2.2 Java中的Queue接口)
[2.2.1 Queue的基本操作](#2.2.1 Queue的基本操作)
[2.2.2 Queue方法对比](#2.2.2 Queue方法对比)
[2.3 队列的模拟实现](#2.3 队列的模拟实现)
[2.3.1 基于链表的队列实现](#2.3.1 基于链表的队列实现)
[2.4 循环队列(Circular Queue)](#2.4 循环队列(Circular Queue))
[2.4.1 循环队列的概念](#2.4.1 循环队列的概念)
[2.4.2 循环队列的实现](#2.4.2 循环队列的实现)
[2.4.3 循环队列的空满判断策略对比](#2.4.3 循环队列的空满判断策略对比)
[2.5 队列的应用场景](#2.5 队列的应用场景)
[2.5.1 线程池任务队列](#2.5.1 线程池任务队列)
[2.5.2 广度优先搜索(BFS)](#2.5.2 广度优先搜索(BFS))
[3.1 Deque的核心概念](#3.1 Deque的核心概念)
[3.2 Java中的Deque实现](#3.2 Java中的Deque实现)
[3.3 Deque的方法体系](#3.3 Deque的方法体系)
[3.4 Deque的应用:滑动窗口最大值](#3.4 Deque的应用:滑动窗口最大值)
[4.1 用队列实现栈](#4.1 用队列实现栈)
[4.2 用栈实现队列](#4.2 用栈实现队列)
[4.3 最小栈](#4.3 最小栈)
[5.1 Stack vs Deque 性能对比](#5.1 Stack vs Deque 性能对比)
[5.2 Queue实现选择指南](#5.2 Queue实现选择指南)
[5.3 时间复杂度总结](#5.3 时间复杂度总结)
[6.1 栈的使用建议](#6.1 栈的使用建议)
[6.2 队列的使用建议](#6.2 队列的使用建议)
一、栈(Stack):后进先出的艺术
1.1 栈的核心概念
栈(Stack) 是一种特殊的线性表,只允许在固定的一端 (栈顶)进行插入和删除操作。数据遵循**后进先出(LIFO)**原则。
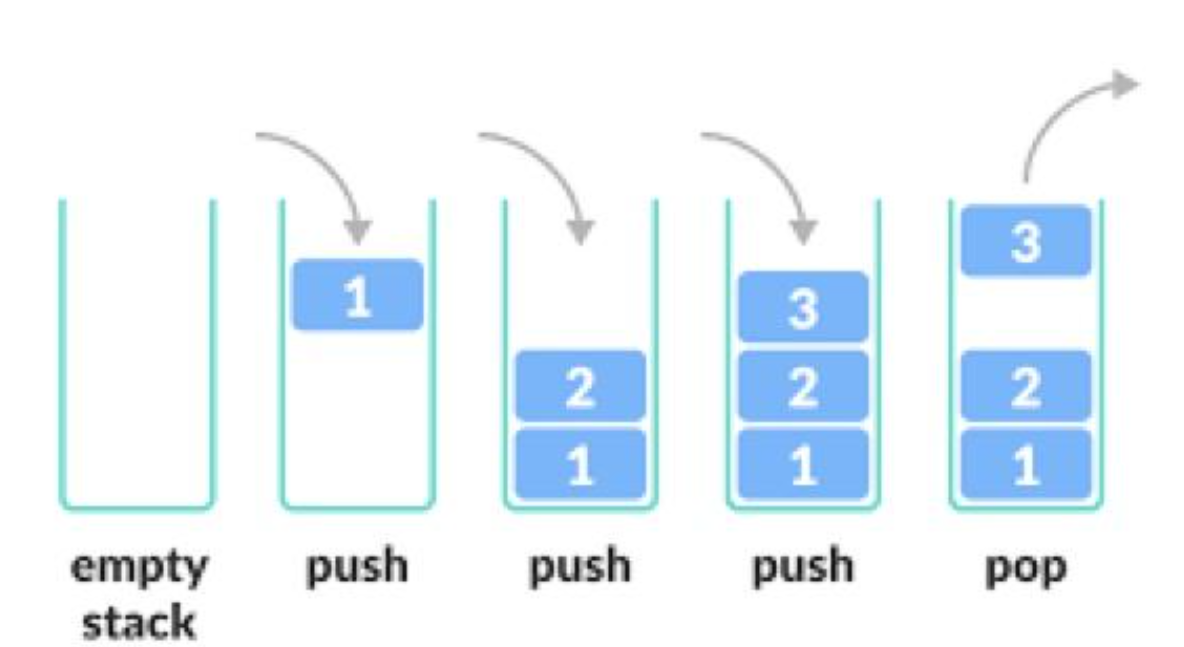
关键术语:
-
压栈(Push):向栈顶添加元素
-
出栈(Pop):从栈顶移除元素
-
栈顶(Top):允许操作的一端
-
栈底(Bottom):不允许操作的一端
1.2 Java中的Stack类
1.2.1 Stack类的基本使用
java
import java.util.Stack;
public class StackDemo {
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
// 压栈操作
stack.push(10); // 栈:[10]
stack.push(20); // 栈:[10, 20]
stack.push(30); // 栈:[10, 20, 30]
// 查看栈顶元素
System.out.println("栈顶元素: " + stack.peek()); // 30
// 出栈操作
int top = stack.pop(); // 移除30
System.out.println("出栈元素: " + top); // 30
// 栈大小
System.out.println("栈大小: " + stack.size()); // 2
// 判断栈是否为空
System.out.println("栈是否为空: " + stack.isEmpty()); // false
}
}1.2.2 Stack的继承关系(重要补充)
java
// Stack类的继承层次
public class Stack<E> extends Vector<E> {
// ...
}
// Vector是线程安全的动态数组
// 这意味着Stack也是线程安全的,但性能较低为什么Stack继承Vector是个设计问题?
-
优点:线程安全
-
缺点:性能开销大(同步锁)
-
现代建议 :使用
Deque接口的实现类代替Stack
java
// 推荐使用Deque作为栈
Deque<Integer> stack = new ArrayDeque<>(); // 性能更好
stack.push(1);
stack.pop();1.3 栈的模拟实现
1.3.1 基于数组的实现(顺序栈)
java
public class ArrayStack<E> {
private Object[] elements; // 存储元素的数组
private int top; // 栈顶指针
private int capacity; // 栈容量
public ArrayStack(int capacity) {
this.capacity = capacity;
this.elements = new Object[capacity];
this.top = -1; // 空栈时top为-1
}
// 压栈操作
public boolean push(E element) {
if (isFull()) {
// 动态扩容
resize();
}
elements[++top] = element;
return true;
}
// 出栈操作
@SuppressWarnings("unchecked")
public E pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
E element = (E) elements[top];
elements[top--] = null; // 帮助GC
return element;
}
// 查看栈顶元素
@SuppressWarnings("unchecked")
public E peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return (E) elements[top];
}
// 栈是否为空
public boolean isEmpty() {
return top == -1;
}
// 栈是否已满
public boolean isFull() {
return top == capacity - 1;
}
// 动态扩容
private void resize() {
int newCapacity = capacity * 2;
elements = Arrays.copyOf(elements, newCapacity);
capacity = newCapacity;
}
}1.3.2 基于链表的实现(链式栈)
java
public class LinkedStack<E> {
// 链表节点
private static class Node<E> {
E data;
Node<E> next;
Node(E data) {
this.data = data;
}
}
private Node<E> top; // 栈顶节点
private int size; // 栈大小
public LinkedStack() {
top = null;
size = 0;
}
// 压栈操作 - O(1)
public void push(E element) {
Node<E> newNode = new Node<>(element);
newNode.next = top; // 新节点指向原栈顶
top = newNode; // 更新栈顶
size++;
}
// 出栈操作 - O(1)
public E pop() {
if (isEmpty()) {
throw new EmptyStackException();
}
E element = top.data;
top = top.next; // 栈顶下移
size--;
return element;
}
// 查看栈顶 - O(1)
public E peek() {
if (isEmpty()) {
throw new EmptyStackException();
}
return top.data;
}
public boolean isEmpty() {
return top == null;
}
public int size() {
return size;
}
}1.4 栈的应用场景(详细扩展)
1.4.1 括号匹配校验器
java
public class BracketChecker {
public static boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (char c : s.toCharArray()) {
// 左括号入栈
if (c == '(' || c == '[' || c == '{') {
stack.push(c);
}
// 右括号检查匹配
else if (c == ')' && !stack.isEmpty() && stack.peek() == '(') {
stack.pop();
} else if (c == ']' && !stack.isEmpty() && stack.peek() == '[') {
stack.pop();
} else if (c == '}' && !stack.isEmpty() && stack.peek() == '{') {
stack.pop();
} else {
return false; // 不匹配
}
}
return stack.isEmpty(); // 栈为空说明全部匹配
}
// 测试
public static void main(String[] args) {
System.out.println(isValid("()[]{}")); // true
System.out.println(isValid("([)]")); // false
}
}1.4.2 浏览器前进后退功能
java
public class BrowserHistory {
private Stack<String> backStack; // 后退栈
private Stack<String> forwardStack; // 前进栈
private String currentPage;
public BrowserHistory(String homepage) {
backStack = new Stack<>();
forwardStack = new Stack<>();
currentPage = homepage;
}
// 访问新页面
public void visit(String url) {
backStack.push(currentPage);
currentPage = url;
forwardStack.clear(); // 清空前进栈
}
// 后退
public String back(int steps) {
while (steps > 0 && !backStack.isEmpty()) {
forwardStack.push(currentPage);
currentPage = backStack.pop();
steps--;
}
return currentPage;
}
// 前进
public String forward(int steps) {
while (steps > 0 && !forwardStack.isEmpty()) {
backStack.push(currentPage);
currentPage = forwardStack.pop();
steps--;
}
return currentPage;
}
}1.4.3 表达式求值(逆波兰表达式)
java
public class RPNCalculator {
// 计算逆波兰表达式
public static int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for (String token : tokens) {
if (isOperator(token)) {
int b = stack.pop();
int a = stack.pop();
int result = applyOperation(a, b, token);
stack.push(result);
} else {
stack.push(Integer.parseInt(token));
}
}
return stack.pop();
}
private static boolean isOperator(String token) {
return token.equals("+") || token.equals("-") ||
token.equals("*") || token.equals("/");
}
private static int applyOperation(int a, int b, String op) {
switch (op) {
case "+": return a + b;
case "-": return a - b;
case "*": return a * b;
case "/": return a / b;
default: throw new IllegalArgumentException("无效操作符");
}
}
// 中缀转后缀(调度场算法)
public static List<String> infixToPostfix(String[] infix) {
List<String> output = new ArrayList<>();
Stack<String> operators = new Stack<>();
Map<String, Integer> precedence = new HashMap<>();
precedence.put("+", 1);
precedence.put("-", 1);
precedence.put("*", 2);
precedence.put("/", 2);
for (String token : infix) {
if (isNumber(token)) {
output.add(token);
} else if (token.equals("(")) {
operators.push(token);
} else if (token.equals(")")) {
while (!operators.peek().equals("(")) {
output.add(operators.pop());
}
operators.pop(); // 弹出"("
} else {
while (!operators.isEmpty() &&
!operators.peek().equals("(") &&
precedence.getOrDefault(operators.peek(), 0) >=
precedence.getOrDefault(token, 0)) {
output.add(operators.pop());
}
operators.push(token);
}
}
while (!operators.isEmpty()) {
output.add(operators.pop());
}
return output;
}
}1.5 重要概念区分
| 概念 | 定义 | 特点 |
|---|---|---|
| 数据结构栈 | 后进先出的线性表 | 用于算法设计,如DFS、表达式求值 |
| JVM栈 | Java虚拟机内存区域 | 存储局部变量、操作数栈、方法出口等 |
| 栈帧 | 方法调用的基本单位 | 包含局部变量表、操作数栈、动态链接、返回地址 |
| 线程栈 | 每个线程私有的栈 | 存储线程执行的方法调用信息 |
java
// JVM栈的简单理解
public class JVMStackDemo {
public static void main(String[] args) {
// main方法栈帧
int x = 10;
method1(x); // 创建method1的栈帧
}
static void method1(int param) {
// method1栈帧
int y = 20;
method2(y); // 创建method2的栈帧
}
static void method2(int param) {
// method2栈帧
System.out.println(param);
}
}二、队列(Queue):先进先出的哲学
2.1 队列的核心概念
队列(Queue) 是一种只允许在一端(队尾)插入,在另一端(队头)删除的线性表,遵循**先进先出(FIFO)**原则。
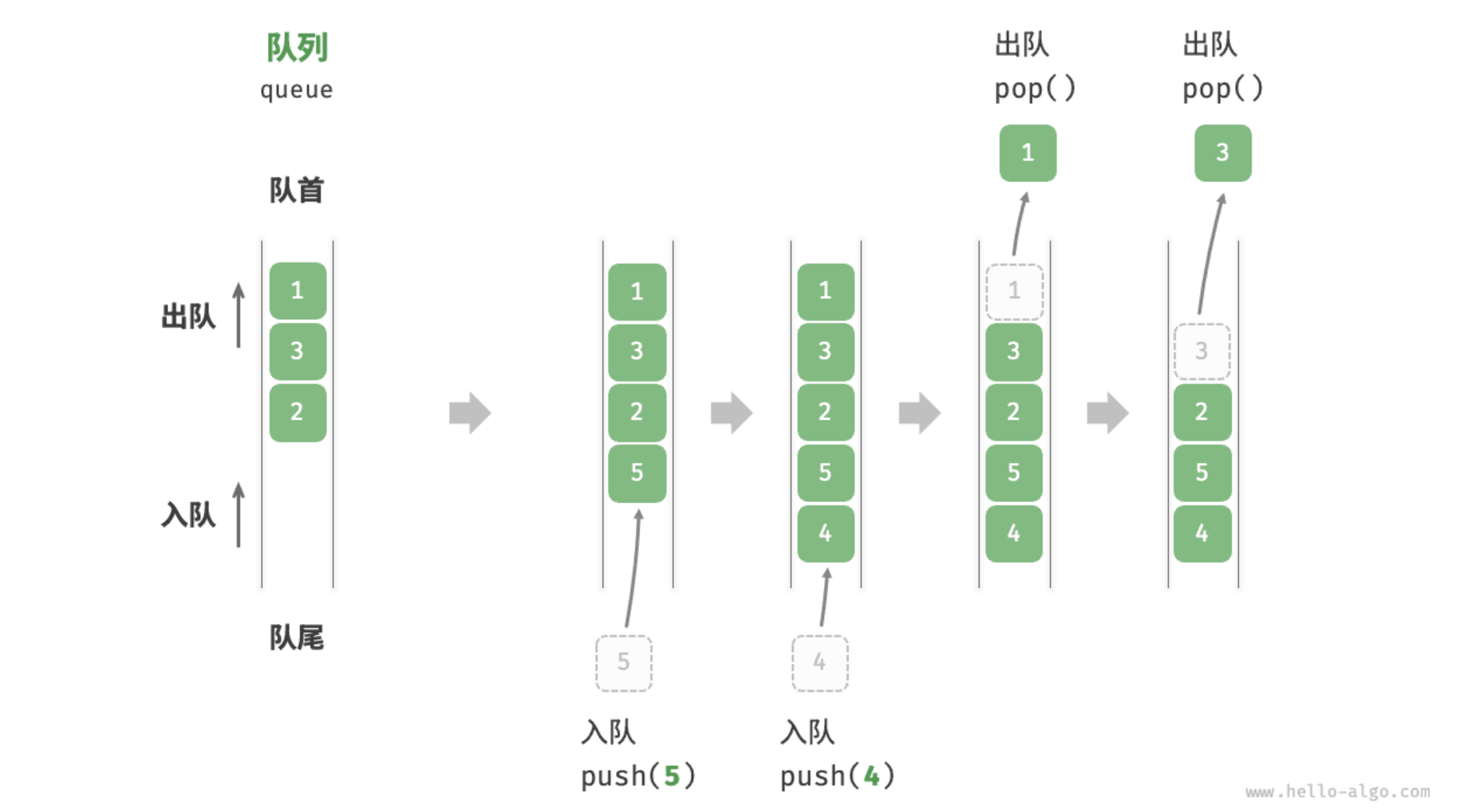
2.2 Java中的Queue接口
2.2.1 Queue的基本操作
java
import java.util.LinkedList;
import java.util.Queue;
public class QueueDemo {
public static void main(String[] args) {
Queue<Integer> queue = new LinkedList<>();
// 入队操作
queue.offer(10); // 队列:[10]
queue.offer(20); // 队列:[10, 20]
queue.offer(30); // 队列:[10, 20, 30]
// 查看队头元素
System.out.println("队头元素: " + queue.peek()); // 10
// 出队操作
int front = queue.poll(); // 移除10
System.out.println("出队元素: " + front); // 10
// 队列大小
System.out.println("队列大小: " + queue.size()); // 2
// 判断队列是否为空
System.out.println("队列是否为空: " + queue.isEmpty()); // false
// 遍历队列
System.out.print("队列元素: ");
for (Integer num : queue) {
System.out.print(num + " "); // 20 30
}
}
}2.2.2 Queue方法对比
| 方法 | 功能 | 异常处理 |
|---|---|---|
add(e) |
入队,失败时抛出异常 | IllegalStateException |
offer(e) |
入队,失败时返回false | 无异常 |
remove() |
出队,空队列时抛出异常 | NoSuchElementException |
poll() |
出队,空队列时返回null | 无异常 |
element() |
查看队头,空队列时抛异常 | NoSuchElementException |
peek() |
查看队头,空队列时返回null | 无异常 |
推荐使用 :offer()、poll()、peek(),避免异常处理
2.3 队列的模拟实现
2.3.1 基于链表的队列实现
java
public class LinkedQueue<E> {
// 链表节点
private static class Node<E> {
E data;
Node<E> next;
Node(E data) {
this.data = data;
}
}
private Node<E> head; // 队头
private Node<E> tail; // 队尾
private int size;
public LinkedQueue() {
head = tail = null;
size = 0;
}
// 入队操作 - O(1)
public boolean offer(E element) {
Node<E> newNode = new Node<>(element);
if (tail == null) {
// 空队列
head = tail = newNode;
} else {
tail.next = newNode;
tail = newNode;
}
size++;
return true;
}
// 出队操作 - O(1)
public E poll() {
if (isEmpty()) {
return null;
}
E element = head.data;
head = head.next;
if (head == null) {
tail = null; // 队列已空
}
size--;
return element;
}
// 查看队头 - O(1)
public E peek() {
if (isEmpty()) {
return null;
}
return head.data;
}
public boolean isEmpty() {
return head == null;
}
public int size() {
return size;
}
}2.4 循环队列(Circular Queue)
2.4.1 循环队列的概念
普通队列使用数组实现时,出队操作会导致"假溢出"(数组前面有空位但后面已满)。循环队列通过循环利用数组空间解决这个问题。
java
// 循环队列示意图
初始状态: [null, null, null, null, null]
↑head
↑tail
入队a,b,c: [a, b, c, null, null]
↑head ↑tail
出队a: [null, b, c, null, null]
↑head ↑tail
入队d,e: [e, b, c, d, null] // e循环到数组开头
↑tail ↑head2.4.2 循环队列的实现
java
public class CircularQueue<E> {
private Object[] elements;
private int head; // 队头索引
private int tail; // 队尾索引
private int size; // 元素个数
private int capacity;
public CircularQueue(int capacity) {
this.capacity = capacity;
this.elements = new Object[capacity];
this.head = this.tail = 0;
this.size = 0;
}
// 入队操作
public boolean offer(E element) {
if (isFull()) {
return false;
}
elements[tail] = element;
tail = (tail + 1) % capacity; // 循环移动
size++;
return true;
}
// 出队操作
@SuppressWarnings("unchecked")
public E poll() {
if (isEmpty()) {
return null;
}
E element = (E) elements[head];
elements[head] = null; // 帮助GC
head = (head + 1) % capacity; // 循环移动
size--;
return element;
}
// 判断队列是否为空
public boolean isEmpty() {
return size == 0;
}
// 判断队列是否已满
public boolean isFull() {
return size == capacity;
}
// 查看队头元素
@SuppressWarnings("unchecked")
public E peek() {
if (isEmpty()) {
return null;
}
return (E) elements[head];
}
// 获取队列大小
public int size() {
return size;
}
// 清空队列
public void clear() {
for (int i = 0; i < capacity; i++) {
elements[i] = null;
}
head = tail = 0;
size = 0;
}
}2.4.3 循环队列的空满判断策略对比
| 策略 | 实现方式 | 优点 | 缺点 |
|---|---|---|---|
| size计数法 | 维护size变量 | 逻辑简单,判断准确 | 需要额外空间 |
| 空一位法 | tail+1=head为满 | 不需要size变量 | 浪费一个数组位置 |
| 标志位法 | 使用flag标记 | 可区分空和满 | 逻辑复杂 |
推荐使用size计数法,代码清晰易懂。
2.5 队列的应用场景
2.5.1 线程池任务队列
java
public class ThreadPool {
private final Queue<Runnable> taskQueue;
private final List<WorkerThread> threads;
private volatile boolean isShutdown;
public ThreadPool(int poolSize) {
taskQueue = new LinkedList<>();
threads = new ArrayList<>();
isShutdown = false;
// 创建工作线程
for (int i = 0; i < poolSize; i++) {
WorkerThread thread = new WorkerThread();
thread.start();
threads.add(thread);
}
}
// 提交任务
public void execute(Runnable task) {
if (isShutdown) {
throw new IllegalStateException("线程池已关闭");
}
synchronized (taskQueue) {
taskQueue.offer(task);
taskQueue.notify(); // 唤醒等待的工作线程
}
}
// 工作线程
private class WorkerThread extends Thread {
@Override
public void run() {
while (!isShutdown || !taskQueue.isEmpty()) {
Runnable task = null;
synchronized (taskQueue) {
while (taskQueue.isEmpty() && !isShutdown) {
try {
taskQueue.wait(); // 等待任务
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
return;
}
}
task = taskQueue.poll();
}
if (task != null) {
try {
task.run();
} catch (Exception e) {
e.printStackTrace();
}
}
}
}
}
// 关闭线程池
public void shutdown() {
isShutdown = true;
synchronized (taskQueue) {
taskQueue.notifyAll(); // 唤醒所有等待线程
}
}
}2.5.2 广度优先搜索(BFS)
java
public class BFS {
// 图的节点
static class Node {
int value;
List<Node> neighbors;
Node(int value) {
this.value = value;
this.neighbors = new ArrayList<>();
}
}
// BFS遍历
public static void bfs(Node start) {
if (start == null) return;
Queue<Node> queue = new LinkedList<>();
Set<Node> visited = new HashSet<>();
queue.offer(start);
visited.add(start);
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
Node current = queue.poll();
System.out.print(current.value + " ");
// 访问邻居节点
for (Node neighbor : current.neighbors) {
if (!visited.contains(neighbor)) {
queue.offer(neighbor);
visited.add(neighbor);
}
}
}
System.out.println(); // 换行表示新的一层
}
}
// 寻找最短路径
public static int shortestPath(Node start, Node target) {
Queue<Node> queue = new LinkedList<>();
Map<Node, Integer> distances = new HashMap<>();
queue.offer(start);
distances.put(start, 0);
while (!queue.isEmpty()) {
Node current = queue.poll();
int currentDist = distances.get(current);
if (current == target) {
return currentDist;
}
for (Node neighbor : current.neighbors) {
if (!distances.containsKey(neighbor)) {
distances.put(neighbor, currentDist + 1);
queue.offer(neighbor);
}
}
}
return -1; // 不可达
}
}三、双端队列(Deque):两端操作的灵活性
3.1 Deque的核心概念
**双端队列(Deque)**允许在队头和队尾都可以进行插入和删除操作,结合了栈和队列的特性。
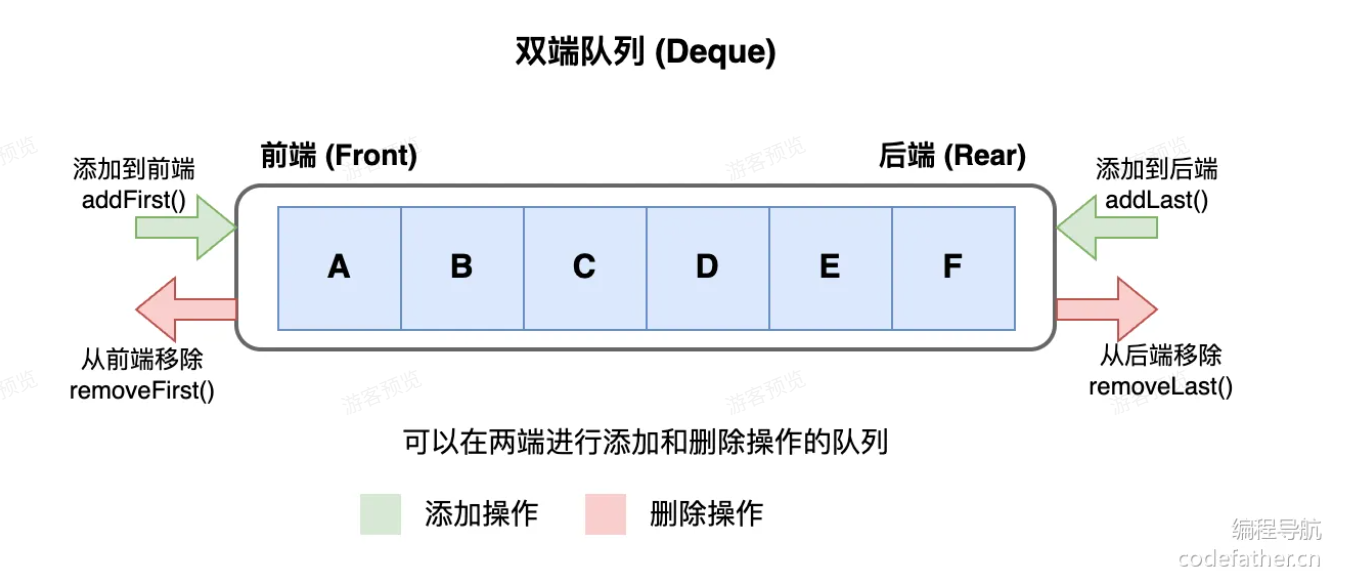
3.2 Java中的Deque实现
Java提供了两种主要实现:
-
ArrayDeque:基于可扩容数组,性能好
-
LinkedList:基于双向链表,功能更全面
java
import java.util.ArrayDeque;
import java.util.Deque;
public class DequeDemo {
public static void main(String[] args) {
// 作为栈使用
Deque<Integer> stack = new ArrayDeque<>();
stack.push(1); // 压栈
stack.push(2);
System.out.println(stack.pop()); // 2 (出栈)
// 作为队列使用
Deque<Integer> queue = new ArrayDeque<>();
queue.offer(1); // 入队
queue.offer(2);
System.out.println(queue.poll()); // 1 (出队)
// 双端操作
Deque<Integer> deque = new ArrayDeque<>();
deque.addFirst(1); // 头部添加
deque.addLast(2); // 尾部添加
System.out.println(deque.removeFirst()); // 1
System.out.println(deque.removeLast()); // 2
}
}3.3 Deque的方法体系
| 操作类型 | 队头操作 | 队尾操作 | 说明 |
|---|---|---|---|
| 插入 | addFirst(e) |
addLast(e) |
失败时抛出异常 |
offerFirst(e) |
offerLast(e) |
失败时返回false | |
| 删除 | removeFirst() |
removeLast() |
空队列时抛异常 |
pollFirst() |
pollLast() |
空队列时返回null | |
| 查看 | getFirst() |
getLast() |
空队列时抛异常 |
peekFirst() |
peekLast() |
空队列时返回null |
3.4 Deque的应用:滑动窗口最大值
java
public class SlidingWindow {
// 使用双端队列维护窗口最大值
public static int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0 || k <= 0) {
return new int[0];
}
int n = nums.length;
int[] result = new int[n - k + 1];
Deque<Integer> deque = new ArrayDeque<>(); // 存储索引
for (int i = 0; i < n; i++) {
// 移除窗口外的元素
while (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {
deque.pollFirst();
}
// 保持队列递减(从大到小)
while (!deque.isEmpty() && nums[deque.peekLast()] <= nums[i]) {
deque.pollLast();
}
// 添加当前元素索引
deque.offerLast(i);
// 记录窗口最大值
if (i >= k - 1) {
result[i - k + 1] = nums[deque.peekFirst()];
}
}
return result;
}
public static void main(String[] args) {
int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
int k = 3;
int[] result = maxSlidingWindow(nums, k);
// 输出: [3, 3, 5, 5, 6, 7]
}
}四、经典面试题实现
4.1 用队列实现栈
java
class MyStack {
private Queue<Integer> queue;
public MyStack() {
queue = new LinkedList<>();
}
// 方法1:每次入栈时重新排列队列
public void push(int x) {
int size = queue.size();
queue.offer(x);
// 将前面的元素依次移到后面
for (int i = 0; i < size; i++) {
queue.offer(queue.poll());
}
}
// 方法2:使用两个队列
class MyStack2 {
private Queue<Integer> mainQueue;
private Queue<Integer> helperQueue;
public MyStack2() {
mainQueue = new LinkedList<>();
helperQueue = new LinkedList<>();
}
public void push(int x) {
helperQueue.offer(x);
// 将主队列所有元素移到辅助队列
while (!mainQueue.isEmpty()) {
helperQueue.offer(mainQueue.poll());
}
// 交换两个队列
Queue<Integer> temp = mainQueue;
mainQueue = helperQueue;
helperQueue = temp;
}
public int pop() {
return mainQueue.poll();
}
public int top() {
return mainQueue.peek();
}
public boolean empty() {
return mainQueue.isEmpty();
}
}
public int pop() {
return queue.poll();
}
public int top() {
return queue.peek();
}
public boolean empty() {
return queue.isEmpty();
}
}4.2 用栈实现队列
java
class MyQueue {
private Stack<Integer> inStack; // 输入栈
private Stack<Integer> outStack; // 输出栈
public MyQueue() {
inStack = new Stack<>();
outStack = new Stack<>();
}
// 入队:直接压入输入栈
public void push(int x) {
inStack.push(x);
}
// 出队:如果输出栈为空,将输入栈所有元素弹出并压入输出栈
public int pop() {
if (outStack.isEmpty()) {
transfer();
}
return outStack.pop();
}
// 查看队头
public int peek() {
if (outStack.isEmpty()) {
transfer();
}
return outStack.peek();
}
// 转移元素
private void transfer() {
while (!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
// 判断队列是否为空
public boolean empty() {
return inStack.isEmpty() && outStack.isEmpty();
}
}4.3 最小栈
java
class MinStack {
private Stack<Integer> dataStack; // 数据栈
private Stack<Integer> minStack; // 最小栈
public MinStack() {
dataStack = new Stack<>();
minStack = new Stack<>();
}
public void push(int val) {
dataStack.push(val);
// 如果最小栈为空或当前值更小,则入栈
if (minStack.isEmpty() || val <= minStack.peek()) {
minStack.push(val);
}
}
public void pop() {
if (dataStack.isEmpty()) return;
int val = dataStack.pop();
// 如果弹出的是最小值,最小栈也弹出
if (val == minStack.peek()) {
minStack.pop();
}
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
// 优化版:只用一个栈存储差值
class MinStackOptimized {
private Stack<Long> stack;
private long min;
public MinStackOptimized() {
stack = new Stack<>();
}
public void push(int val) {
if (stack.isEmpty()) {
stack.push(0L);
min = val;
} else {
long diff = val - min;
stack.push(diff);
if (diff < 0) {
min = val; // 更新最小值
}
}
}
public void pop() {
long diff = stack.pop();
if (diff < 0) {
// 当前弹出的是最小值,需要恢复前一个最小值
min = min - diff;
}
}
public int top() {
long diff = stack.peek();
if (diff < 0) {
return (int) min;
} else {
return (int) (min + diff);
}
}
public int getMin() {
return (int) min;
}
}五、性能对比与选择指南
5.1 Stack vs Deque 性能对比
| 操作 | Stack (继承Vector) | ArrayDeque | LinkedList | 推荐 |
|---|---|---|---|---|
| push/pop | O(1) 同步开销大 | O(1) 平摊 | O(1) | ArrayDeque |
| 随机访问 | O(1) | O(1) | O(n) | ArrayDeque |
| 内存占用 | 较少 | 较少 | 较多(节点开销) | ArrayDeque |
| 线程安全 | 是 | 否 | 否 | 无并发用ArrayDeque |
结论 :优先使用ArrayDeque作为栈的实现。
5.2 Queue实现选择指南
| 场景 | 推荐实现 | 理由 |
|---|---|---|
| 一般队列 | LinkedList | 功能完整,支持null元素 |
| 高并发队列 | ConcurrentLinkedQueue | 线程安全,无锁 |
| 有界队列 | ArrayBlockingQueue | 固定大小,阻塞操作 |
| 延迟队列 | DelayQueue | 支持延迟获取元素 |
| 优先级队列 | PriorityQueue | 按优先级出队 |
5.3 时间复杂度总结
| 数据结构 | 压栈/入队 | 出栈/出队 | 查看栈顶/队头 | 随机访问 |
|---|---|---|---|---|
| ArrayStack | O(1)平摊 | O(1) | O(1) | O(1) |
| LinkedStack | O(1) | O(1) | O(1) | O(n) |
| ArrayQueue | O(1) | O(n)需搬移 | O(1) | O(1) |
| CircularQueue | O(1) | O(1) | O(1) | O(1) |
| LinkedQueue | O(1) | O(1) | O(1) | O(n) |
| ArrayDeque | O(1)平摊 | O(1) | O(1) | O(1) |
六、实际开发建议
6.1 栈的使用建议
java
// 1. 优先使用Deque而不是Stack
Deque<Integer> stack = new ArrayDeque<>(); // ✓
Stack<Integer> stack = new Stack<>(); // ✗(过时)
// 2. 初始容量预估
Deque<Integer> stack = new ArrayDeque<>(100); // 预估初始容量
// 3. 栈的典型应用模式
public class StackPatterns {
// 模式1:对称性匹配(括号、标签等)
public boolean isValid(String s) {
Deque<Character> stack = new ArrayDeque<>();
// ... 括号匹配逻辑
}
// 模式2:撤销/重做功能
public class Editor {
Deque<String> undoStack = new ArrayDeque<>();
Deque<String> redoStack = new ArrayDeque<>();
public void edit(String content) {
undoStack.push(content);
redoStack.clear(); // 新编辑清空重做栈
}
}
// 模式3:深度优先遍历
public void dfs(Node root) {
Deque<Node> stack = new ArrayDeque<>();
stack.push(root);
while (!stack.isEmpty()) {
Node node = stack.pop();
// 处理节点
for (Node child : node.children) {
stack.push(child);
}
}
}
}6.2 队列的使用建议
java
// 1. 根据场景选择合适的队列实现
Queue<String> queue = new LinkedList<>(); // 一般队列
BlockingQueue<String> bq = new ArrayBlockingQueue<>(100); // 有界阻塞队列
// 2. 生产者-消费者模式
public class ProducerConsumer {
private final BlockingQueue<Integer> queue = new ArrayBlockingQueue<>(10);
class Producer implements Runnable {
public void run() {
try {
for (int i = 0; i < 100; i++) {
queue.put(i); // 阻塞直到有空间
System.out.println("生产: " + i);
}
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
}
class Consumer implements Runnable {
public void run() {
try {
while (true) {
Integer item = queue.take(); // 阻塞直到有元素
System.out.println("消费: " + item);
}
} catch (InterruptedException e) {
Thread.currentThread().interrupt();
}
}
}
}
// 3. 任务调度队列
public class TaskScheduler {
private final PriorityQueue<Task> taskQueue = new PriorityQueue<>(
Comparator.comparing(Task::getPriority)
);
public void schedule(Task task) {
taskQueue.offer(task);
}
public Task getNextTask() {
return taskQueue.poll();
}
}总结
核心要点总结:
-
栈(Stack):LIFO(后进先出),适合对称性处理、递归转循环、撤销操作等场景
-
队列(Queue):FIFO(先进先出),适合任务调度、BFS、缓冲等场景
-
双端队列(Deque):两端操作,可同时作为栈和队列使用