一、说明
高维数据变得非常重要。然而,高维空间与我们熟悉的二维和三维空间有很大不同。在d维空间中随机生成n个点,每个坐标都是均值为零、方差为1的高斯分布。当d足够大时,所有点对之间的距离以高概率基本上相同。此外,d维单位球(即所有满足|x|≤1的点x的集合)的体积随着维度的增加而趋近于零。高维单位球的体积集中在它的表面附近,也集中在它的赤道附近。这些性质具有重要的影响,我们将对此进行考虑。
二、大数定律
如果在d维空间中使用高斯分布生成随机点的坐标,当d很大时,所有点对之间的距离将基本上相同。原因是两点y和z之间距离的平方:
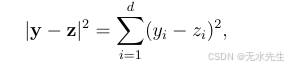
这是d个独立随机变量的总和。如果对一个具有有界方差的随机变量x进行n次独立抽样并取平均值,结果将接近x的期望值。在上述求和中,有d个样本,每个样本是两点y和z在某一坐标上的平方距离。这里我们给出一个称为大数定律的一般性界。具体来说,大数定律指出:
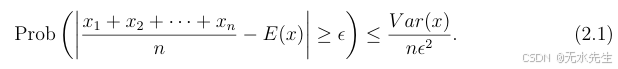
随机变量的方差越大,误差超过某个值的概率就越大。因此,x的方差位于分子。样本数量n位于分母,因为平均的数值越多,差异超过某个值的概率就越小。同样,该值越大,差异超过某个值的概率就越小,因此该值位于分母。请注意,平方运算使该分数成为一个无量纲量。
我们使用两个不等式来证明大数定律。第一个是马尔可夫不等式,它指出非负随机变量超过a的概率受该变量的期望值除以a的限制。
三、证明大数定律
3.1 马尔可夫不等式
定理 2.1(马尔可夫不等式)设 x 是一个非负随机变量。则对于 a > 0,
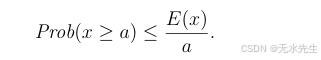
证明:对于一个连续的非负随机变量x,其概率密度为p,
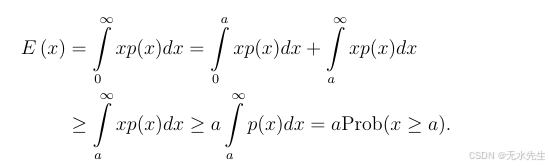
因此,Prob(x≥a)≤E(x)/aProb(x ≥ a) ≤ E(x)/aProb(x≥a)≤E(x)/a。对于离散型随机变量,同样的证明适用于求和而非积分的情况。
推论 2.2 Prob(x≥bE(x))≤1/bProb (x ≥ bE(x) )≤ 1/bProb(x≥bE(x))≤1/b
马尔可夫不等式仅利用分布的均值信息来界分布的尾部。通过同时使用随机变量的方差,可以获得更紧的界。
3.2 切比雪夫不等式
定理 2.3(切比雪夫不等式)设 x 为一个随机变量。则对于 c > 0,
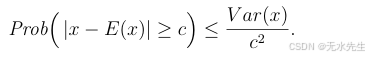
证明:Prob(∣x−E(x)∣≥c)=Prob(∣x−E(x)∣2≥c2)Prob(|x−E(x)| ≥ c) = Prob(|x−E(x)|² ≥ c²)Prob(∣x−E(x)∣≥c)=Prob(∣x−E(x)∣2≥c2) 。令 y=∣x−E(x)∣2y = |x−E(x)|²y=∣x−E(x)∣2。注意到 y 是一个非负随机变量,且 E(y)=Var(x)E(y) = Var(x)E(y)=Var(x),因此可以应用马尔可夫不等式得出:
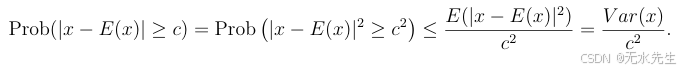
大数定律源于切比雪夫不等式以及关于独立随机变量的事实。回想一下:
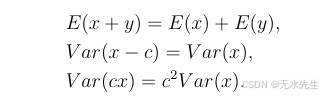
此外,如果x和y相互独立,那么E(xy)=E(x)E(y)E(xy) = E(x)E(y)E(xy)=E(x)E(y)。这些事实意味着,如果x和y相互独立,那么Var(x+y)=Var(x)+Var(y)Var(x + y) = Var(x) + Var(y)Var(x+y)=Var(x)+Var(y),具体推导如下:
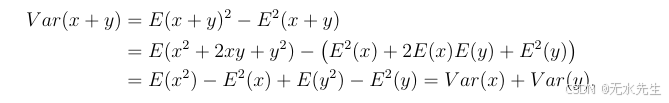
我们利用独立性将E(2xy)替换为2E(x)E(y)。
3.3 证明大数定律
定理2.4(大数定律)设x₁,x₂,...,xₙ是随机变量x的n个独立样本。则
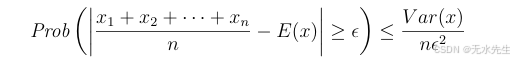
证明:根据切比雪夫不等式
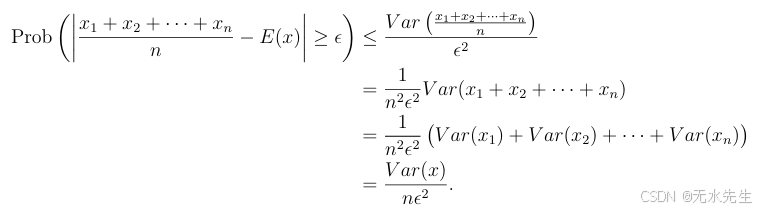
大数定律具有很强的普遍性,适用于任何方差有限的随机变量x。稍后我们将研究球面高斯分布以及0-1取值随机变量之和的更紧致的集中界。
作为大数定律的一个应用,设z是一个d维随机点,其坐标均从均值为零、方差为1/(2π)的高斯分布中选取。我们将方差设为1/(2π),使得该高斯概率密度在原点处等于1,并且在整个单位球内都由一个常数下界。根据大数定律,z到原点的距离的平方以高概率为Θ(d)。特别地,这样的随机点z落在单位球内的概率微乎其微。这意味着概率密度在单位球上的积分也必须微乎其微。另一方面,单位球内的概率密度有一个常数下界。因此,我们可以得出结论:单位球的体积必须微乎其微。
同样,如果我们从一个d维高斯分布中选取两个点y和z,该分布的每个方向方差均为1,那么|y|²≈d,|z|²≈d,且|y−z|²≈2d(因为对所有i,E(yi−zi)²=E(yi²)+E(zi²)−2E(yizi)=2)。因此,根据勾股定理,这些随机的d维向量y和z必须近似正交。这意味着,如果我们把这些随机点缩放为单位长度,并将y称为北极点,那么单位球的大部分表面积必须位于赤道附近。我们将在后续章节中对这些及相关论证进行形式化处理。
我们现在陈述一个关于独立随机变量之和的概率尾界的一般定理。伯努利分布、平方高斯分布和幂律分布随机变量之和的尾界都可以由此推导得出。下表总结了一些结果。
定理 2.5(主尾界定理)设 x=x1+x2+⋅⋅⋅+xnx = x₁ + x₂ + ··· + xₙx=x1+x2+⋅⋅⋅+xn,其中 x1,x2,...,xnx₁, x₂, ..., xₙx1,x2,...,xn 是相互独立的随机变量,均值为零,方差至多为 σ2σ²σ2。令 0≤a≤(2nσ2)0 ≤ a ≤ (\sqrt{2}nσ²)0≤a≤(2 nσ2)。假设对于 s=3,4,...,(a2/(4nσ2))s = 3, 4, ..., (a²/(4nσ²))s=3,4,...,(a2/(4nσ2)),有 ∣E[xis]∣≤σ2/s!|E[xᵢˢ]| ≤ σ²/s!∣E[xis]∣≤σ2/s!。则,
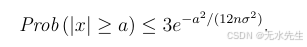
定理12.5的初等证明见附录。为了获得简要的直观理解,考虑将马尔可夫不等式应用于随机变量xrx^rxr,其中r是一个较大的偶数。由于r是偶数,xrx^rxr是非负的,因此Prob(∣x∣≥a)=Prob(xr≥ar)≤E(xr)/arProb(|x| ≥ a) = Prob(x^{r} ≥ a^r) ≤ E(x^{r})/a^rProb(∣x∣≥a)=Prob(xr≥ar)≤E(xr)/ar。如果E(xr)E(x^r)E(xr)不太大,我们就能得到一个较好的界。为了计算E(xr)E(x^r)E(xr),将E(x)写成E(x1+...+xn)rE(x₁ + ... + xₙ)^rE(x1+...+xn)r,并将多项式展开为其各项。利用独立性这一事实:E(xirxjr)=E(xir)E(xjr)E(xᵢʳᵢ xⱼʳⱼ) = E(xᵢʳᵢ)E(xⱼʳⱼ)E(xirxjr)=E(xir)E(xjr),从而得到一组更简单的期望,这些期望可以利用我们的假设∣E(xsi)∣≤σ2s!|E(xₛᵢ)| ≤ σ²s!∣E(xsi)∣≤σ2s!来进行界估计。完整的证明见附录。