路径总和系列（LeetCode 112 & 113 & 437 & 666）

1 概述

本文会介绍路径总和系列的思路以及详细解法。

2 路径总和1

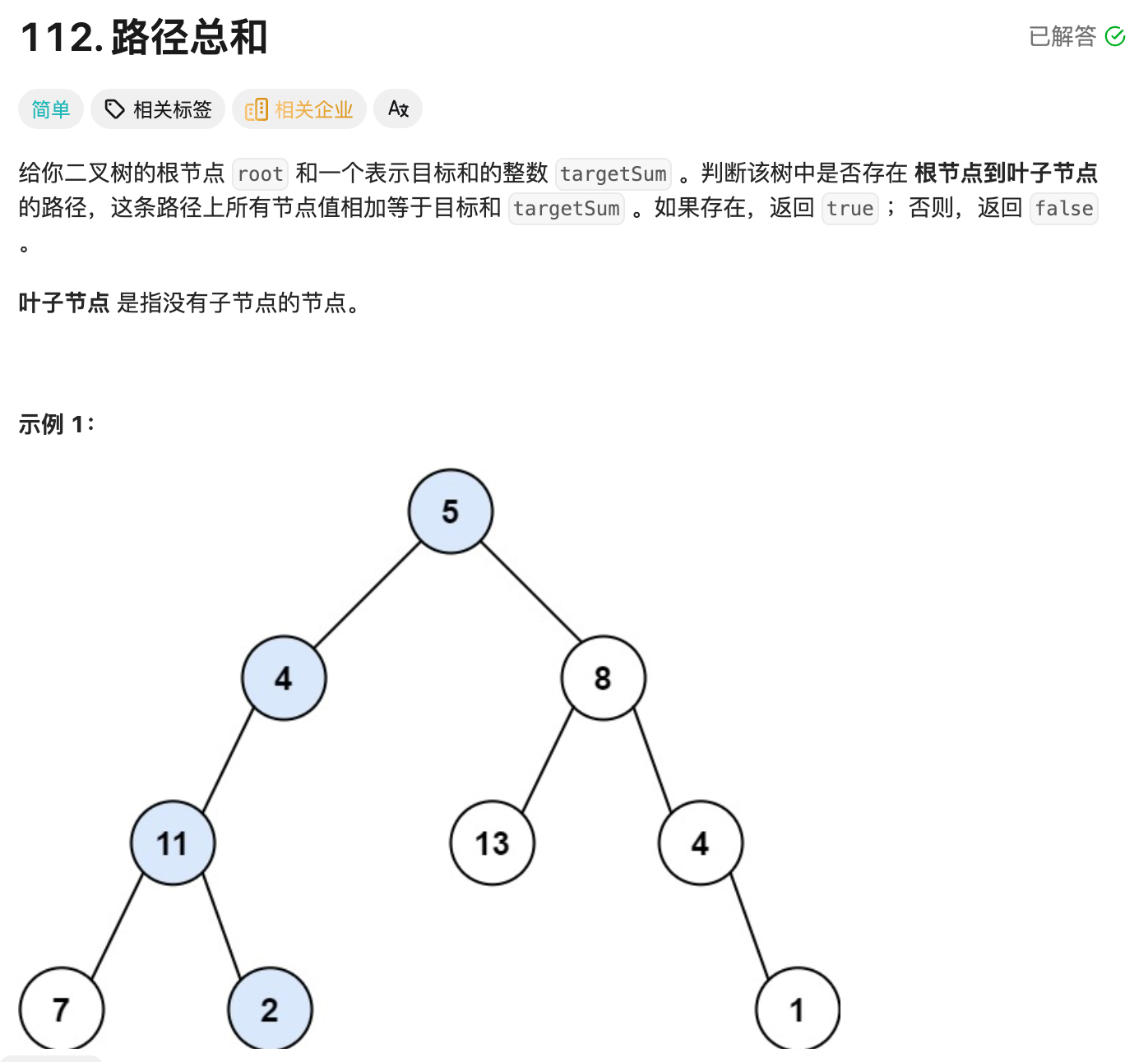
2.1 原题

2.2 思路

整体思路比较简单，在DFS的时候传递从根节点到当前节点的路径和。遍历当前节点的时候，判断加上当前节点的值之后有没有达到targetSum，如果达到的话就直接返回true。

代码如下：

class Solution {
public:
    bool hasPathSum(TreeNode *root, int targetSum) {
        // 结果
        bool res = false;
        // node是当前遍历的节点，s是从根节点到当前节点的累加值
        auto dfs = [&](this auto &&dfs, TreeNode *node, int s) {
            // 如果当前节点为空，或者已经找到结果了，返回
            if (!node || res) {
                return;
            }
            // 如果加上了当前节点的值后等于目标
            // 并且当前节点是叶子节点
            if (s + node->val == targetSum && !node->left && !node->right) {
                // 找到结果，返回
                res = true;
                return;
            }
            // 否则继续向下累加
            dfs(node->left, s + node->val);
            dfs(node->right, s + node->val);
        };
        // 从root开始，和一开始为0
        dfs(root, 0);
        return res;
    }
};

需要注意的点：

• node为空不能和==targetSum写在一个if里面去判断直接返回，不然会出错
• 用例里面会有空的树，不同的写法可能需要额外进行root的判空判断，像这里的写法就不需要

2.3 Java版本

import java.util.*;

public class Solution {
    private boolean res = false;

    private void dfs(TreeNode node, int s, int target) {
        if (node == null || res) {
            return;
        }
        if (s + node.val == target && node.left == null && node.right == null) {
            res = true;
            return;
        }
        dfs(node.left, s + node.val, target);
        dfs(node.right, s + node.val, target);
    }

    public boolean hasPathSum(TreeNode root, int targetSum) {
        dfs(root, 0, targetSum);
        return res;
    }
}

2.4 Go版本

func hasPathSum(root *TreeNode, targetSum int) bool {
	res := false
	var dfs func(*TreeNode, int)
	dfs = func(node *TreeNode, s int) {
		if node == nil || res {
			return
		}
		if s+node.Val == targetSum && node.Left == nil && node.Right == nil {
			res = true
			return
		}
		dfs(node.Left, s+node.Val)
		dfs(node.Right, s+node.Val)
	}
	dfs(root, 0)
	return res
}

3 路径总和2

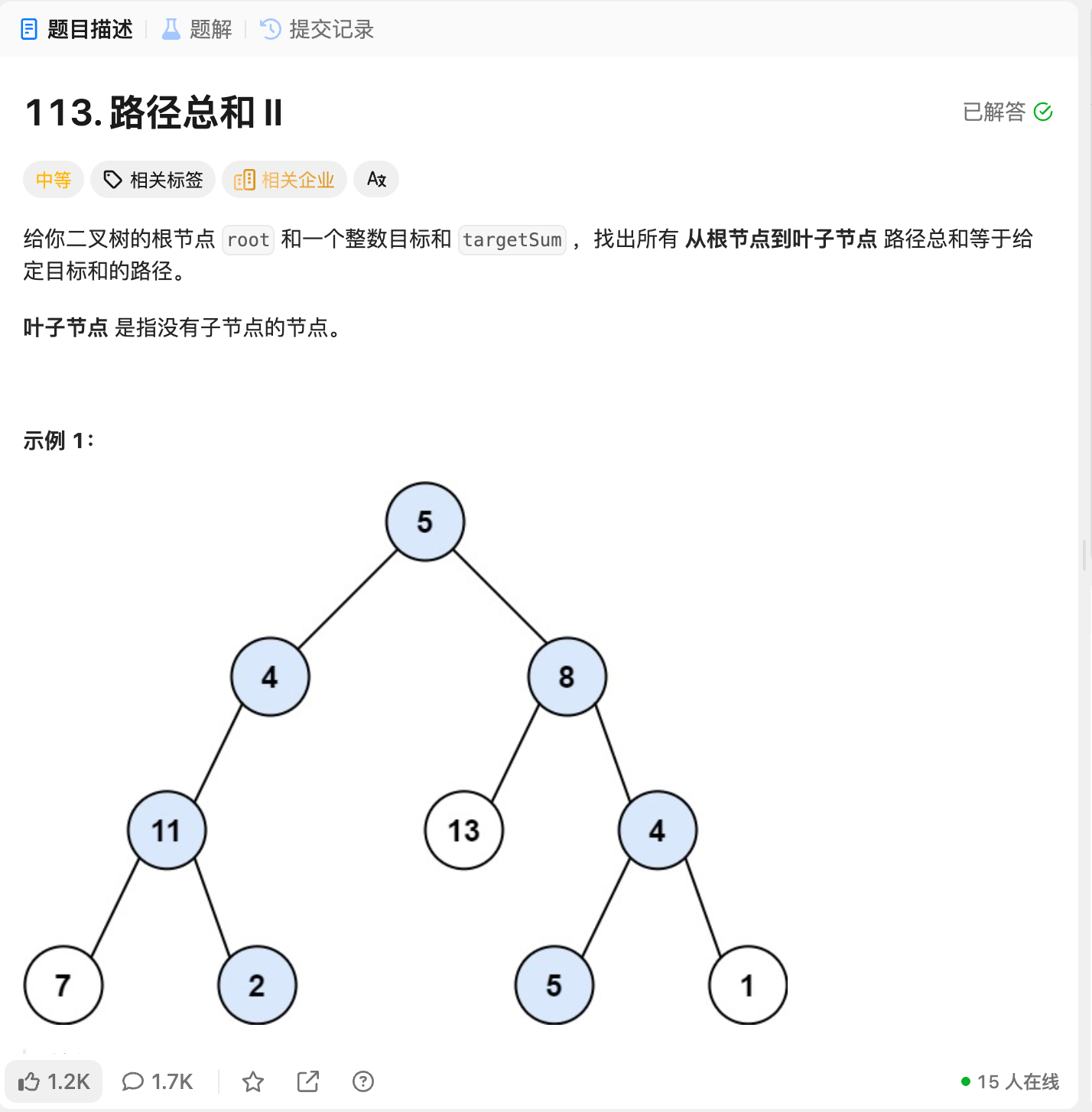
3.1 原题

3.2 思路

本质上和路径总和1是一样的，只不过1是求"有没有"，而路径总和2是求所有路径。

可以使用路径总和1中的方法，在DFS的时候，多传递一个路径参数，存储当前的路径，如果累加得到目标值，将当前的路径加入结果集。

需要注意的点是加入结果集之后需要删除末尾元素（也就是回溯），不然的话最后加入的元素没办法删除，会影响其他节点的遍历结果。

代码如下：

class Solution {
public:
    vector<vector<int> > pathSum(TreeNode *root, int targetSum) {
        // 存储当前路径
        vector<int> cur;
        // 结果集
        vector<vector<int> > res;
        auto dfs = [&](this auto &&dfs, TreeNode *node, int s) {
            // 节点为空，返回
            if (!node) {
                return;
            }
            // 先加入当前节点
            cur.push_back(node->val);
            // 如果得到了目标值，并且是叶子节点
            if (s + node->val == targetSum && !node->left && !node->right) {
                // 加入结果集
                res.push_back(cur);
                // 删除末尾元素
                cur.pop_back();
                return;
            }
            // 遍历左节点和右节点
            dfs(node->left, s + node->val);
            dfs(node->right, s + node->val);
            // 遍历完成后删除末尾元素
            cur.pop_back();
        };
        // 从root开始，和一开始为0
        dfs(root, 0);
        return res;
    }
};

3.3 Java版本

import java.util.*;

public class Solution {
    private final List<List<Integer>> res = new ArrayList<>();
    private final LinkedList<Integer> cur = new LinkedList<>();
    private int targetSum;

    private void dfs(TreeNode node, int s) {
        if (node == null) {
            return;
        }
        cur.addLast(node.val);
        if (s + node.val == targetSum && node.left == null && node.right == null) {
            res.add(new ArrayList<>(cur));
            cur.pollLast();
            return;
        }
        dfs(node.left, s + node.val);
        dfs(node.right, s + node.val);
        cur.pollLast();
    }

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        this.targetSum = targetSum;
        dfs(root, 0);
        return res;
    }
}

3.4 Go版本

func pathSum(root *TreeNode, targetSum int) [][]int {
	res, cur := make([][]int, 0), make([]int, 0)
	var dfs func(*TreeNode, int)
	dfs = func(node *TreeNode, s int) {
		if node == nil {
			return
		}
		cur = append(cur, node.Val)
		if s+node.Val == targetSum && node.Left == nil && node.Right == nil {
			t := make([]int, len(cur))
			copy(t, cur)
			res = append(res, t)
			cur = cur[:len(cur)-1]
			return
		}
		dfs(node.Left, s+node.Val)
		dfs(node.Right, s+node.Val)
		cur = cur[:len(cur)-1]
	}
	dfs(root, 0)
	return res
}

4 路径总和3

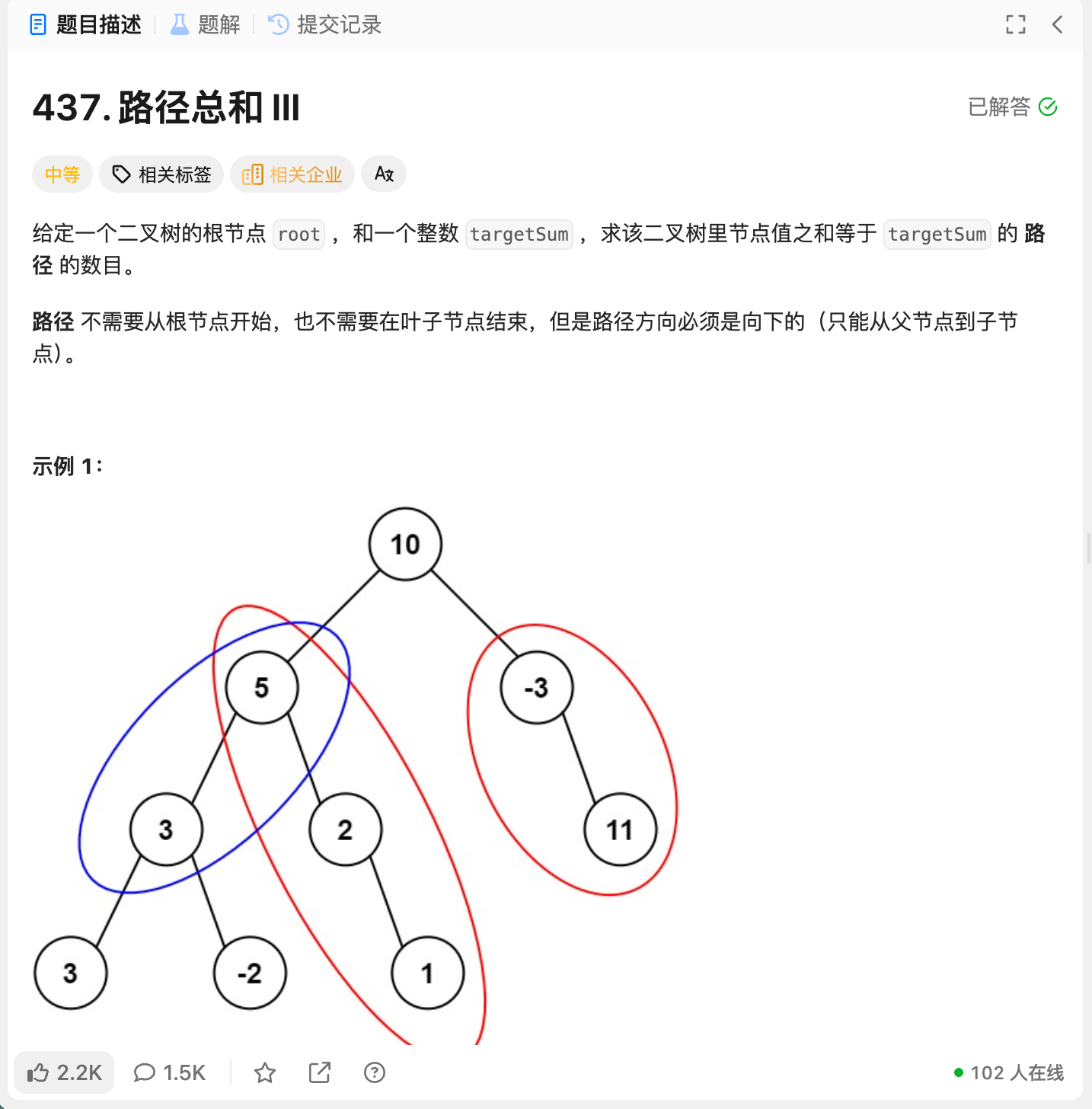
4.1 原题

4.2 思路

路径总和3和之前的1与2都不同，强调了路径不需要从根开始，也不需要到叶子结束，只需要是"向下"即可。

那么一个容易想到的做法就是，从每个节点开始遍历所有路径，使用两个DFS函数：

• dfs1()计算从node开始的所有向下路径，并累加结果
• dfs2()负责遍历树所有的节点，并调用dfs1()

代码如下：

class Solution {
public:
    int pathSum(TreeNode *root, int targetSum) {
        // 结果
        int res = 0;
        // using ll = long long;
        auto dfs1 = [&](this auto &&dfs1, TreeNode *node, ll s) {
            // 节点为空返回
            if (!node) {
                return;
            }
            // 计算路径和
            s += node->val;
            // 如果路径和为目标值，累加结果
            if (s == targetSum) {
                ++res;
            }
            // 遍历左右节点
            dfs1(node->left, s);
            dfs1(node->right, s);
        };
        // dfs2遍历整棵树
        auto dfs2 = [&](this auto &&dfs2, TreeNode *node) {
            if (!node) {
                return;
            }
            // 每遍历一个节点调用一次dfs1()计算向下的路径
            dfs1(node, 0);
            dfs2(node->left);
            dfs2(node->right);
        };
        dfs2(root);
        return res;
    }
};

由于dfs2()时间为O(n)，一次dfs1()时间也是O(n)，所以需要O(n^2)的时间复杂度。

4.3 时间优化

上面介绍的O(n^2)做法实际上就是暴力的做法，暴力的做法其实包含了非常多的无效计算，例如：

• 调用dfs1()找到结果时，如果node下面全部都是正数，其实就不需要计算了
• 同样的一条路径，如果前面包含了很多的0，就会计算了多次，例如targetSum=10，路径为[-1,1,10]、[-2,2,-1,1,10]、[-3,3,-2,2,-1,1,10]，本质上都是[10]这里符合了要求，但是前面的路径和为0，导致了被计算了多次，而实际上这里的计算多次是可以优化的

在上面的例子中，只有[10]是符合要求的，而[-1,1]、[-2,2,-1,1]、[-3,3,-2,2,-1,1]的共同特点是，和为0：

• 和为0，在树中，就表现为路径和为0
• 而在一维数组中，表现为前缀和 为0

这里的前缀和 就是关键，如果知道了前缀和为0的数组（也就是路径）有多少个（路径有多少条），就能直接计算出路径和为targetSum的条数。

假设m[s0]、m[s1]是路径和等于s0、s1的条数，在向下计算（DFS）的时候，如果s1 - s0 == targetSum，也就是发现两条路径s1和s0之差为targetSum的时候，就找到了和为targetSum路径，这条路径的数量就是m[s0]，也就是m[s1-targetSum]。而s1是向下计算的时候累加得到的，所以就可以直接累加m[s1-targetSum]，这个就是答案。

需要注意的点：

• 计算过程中的值会超过int，在C++中需要使用long long
• m[0]需要初始化为1
• 回溯的时候，需要将当前路径和的条数减1

第三点的情况可以考虑如下的树：[1,-2,-3],targetSum=-1，根节点为1，左右节点为-2和-3。

在遍历到-3的时候，有：

• m[0]=1
• m[1]=1
• m[-1]=1
• m[-2]=1

根据当前的算法，在遍历到3这个节点的时候，s=-2，而m[s-targetSum]等于m[-1]，也就是1，由于在遍历到-2的时候也有一个答案1，所以最终答案就是2，很明显这是个错误的答案。

原因就在于在遍历完成-2节点回溯的时候，没有累加当前的路径和，如果累减了，m[-1]=0，最终答案就是1，这个才是正确的答案。

代码如下：

class Solution {
public:
    int pathSum(TreeNode *root, int targetSum) {
        // using ll = long long;
        // key,value = 路径和,数量
        unordered_map<ll, int> m;
        // 结果
        int res = 0;
        // 路径和为0的数量为1，用于计算刚好等于targetSum的时候路径的数量
        // 例如targetSum = 10，计算得到了s=10，res+=m[s-targetSum]等价于res+=m[0]，也就是发现了一条路径
        m[0] = 1;
        auto dfs = [&](this auto &&dfs, TreeNode *node, ll s) {
            // 当前节点为空，返回
            if (!node) {
                return;
            }
            // 累加当前路径和
            s += node->val;
            // 计算结果，如果存在s-targetSum的key，表明有value条路径是等于targetSum的
            res += m[s - targetSum];
            // 路径和为s的条数+1
            ++m[s];
            // 遍历左右节点
            dfs(node->left, s);
            dfs(node->right, s);
            // 回溯的时候需要将条数减1
            --m[s];
        };
        dfs(root, 0);
        return res;
    }
};

这个做法牺牲了空间（O(n)），但是换来了时间复杂度的优化，从O(n^2)优化到了O(n)。

4.4 Java版本

import java.util.*;

public class Solution {
    private final Map<Long, Integer> m = new HashMap<>();
    private int res = 0;
    private int targetSum;

    private void dfs(TreeNode node, long s) {
        if (node == null) {
            return;
        }
        s += node.val;
        res += m.getOrDefault(s - targetSum, 0);
        m.merge(s, 1, Integer::sum);
        dfs(node.left, s);
        dfs(node.right, s);
        m.merge(s, -1, Integer::sum);
    }

    public int pathSum(TreeNode root, int targetSum) {
        this.targetSum = targetSum;
        m.put(0L, 1);
        dfs(root, 0);
        return res;
    }
}

4.5 Go版本

func pathSum(root *TreeNode, targetSum int) int {
	res, m := 0, make(map[int64]int)
	m[0] = 1
	var dfs func(*TreeNode, int64)
	dfs = func(node *TreeNode, s int64) {
		if node == nil {
			return
		}
		s += int64(node.Val)
		res += m[s-int64(targetSum)]
		m[s]++
		dfs(node.Left, s)
		dfs(node.Right, s)
		m[s]--
	}
	dfs(root, 0)
	return res
}

5 路径总和4

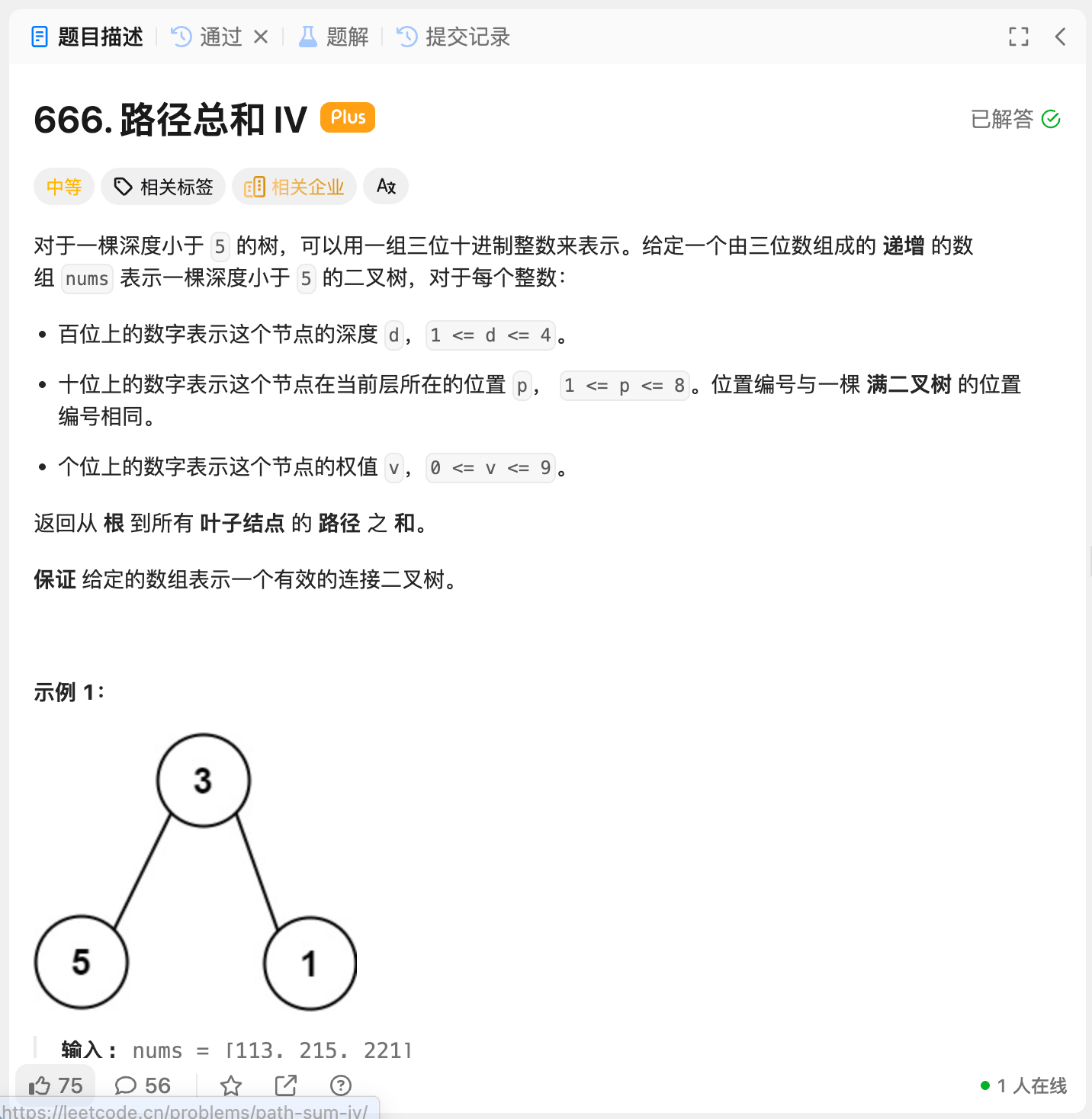
5.1 原题

这题是VIP题目，没有VIP可以参考此处。

5.2 思路

这道题本身不难，本质上就是路径总和1，直接对树进行DFS即可得出答案。

但是这道题需要转换一下，因为给出的不是一颗直接的树而是数组，那就根据题意构建树即可。

本题中，每个节点使用了三个参数表示：

• 深度d：节点的深度，根深度为1，计算方式/100
• 位置p：这个参数比较重要，标识节点的位置，计算方式%100 /10，由于1<=p<=8，父节点的位置为(p+1)/2，左孩子节点位置为p*2-1和p*2
• 节点值v：节点本身的值，直接%10可以得到

只要知道了位置p和对应父子节点的关系，就能构建出这棵树。

实现时需要注意的细节：

• 使用一个二维数组存储节点即可
• 由于已经排序，所以第一个就是根节点
• 根节点固定前两个参数是11
• 尽管函数参数没有TreeNode，但是TreeNode是自带的，（对于C++来说）不需要额外的#include，在别的题目也一样

代码如下：

class Solution {
public:
    int pathSum(vector<int> &nums) {
        // 存储节点
        vector tree(5, vector<TreeNode *>(9, nullptr));
        // 根节点
        const auto root = new TreeNode(nums[0] % 10);
        // 根节点固定是[1][1]
        tree[1][1] = root;
        // 从第二个节点开始遍历
        for (int i = 1, n = static_cast<int>(nums.size()); i < n; ++i) {
            // 深度
            const int d = nums[i] / 100;
            // 位置
            const int p = nums[i] % 100 / 10;
            // 节点值
            const int v = nums[i] % 10;
            // 创建节点
            const auto node = new TreeNode(v);
            // p是奇数，等价于是父节点的左节点
            // 记得深度需要减1，父节点的位置之前提过，(p+1)/2，和(p+1)>>1等价
            if (p & 1) {
                tree[d - 1][(p + 1) >> 1]->left = node;
            } else {
                // 否则右节点
                tree[d - 1][(p + 1) >> 1]->right = node;
            }
            // 将自身存储到深度为d，位置为p的地方
            tree[d][p] = node;
        }
        int res = 0;
        // 简单深搜
        auto dfs = [&](this auto &&dfs, TreeNode *node, int cur) {
            if (!node) {
                return;
            }
            // 累加节点值
            cur += node->val;
            // 遇到叶子节点
            if (!node->left && !node->right) {
                // 累加结果
                res += cur;
                return;
            }
            dfs(node->left, cur);
            dfs(node->right, cur);
        };
        dfs(root, 0);
        return res;
    }
};

5.3 贡献法

另一种思路是，不直接构建整棵树进行深搜，而是对每个节点，单独计算对结果的贡献。

由于答案是计算总和，而总和等于每个节点的值乘以每个节点的出现次数（也就是路径经过次数），所以计算出一个节点有多少条路径经过即可。

一个节点的路径经过次数，可以从子节点累加得到。初始化当前节点的经过次数为0，遍历时：

• 如果为0，设置为1
• 如果不为0，不处理

得到次数后累加到父节点的出现次数上。

这个计算的逻辑是，一个节点的路径经过次数，是由子节点决定的，子节点越多，路径经过次数越多。而一个子节点，可以理解成多一条路径经过。另一方面，路径的经过次数是逐级往上累加的，深度越小的节点，经过次数越多。

之所以设置为0，是因为如果设置为1，会重复多计算一次，造成结果值偏大。

代码如下：

class Solution {
public:
    int pathSum(vector<int> &nums) {
        // 存储节点
        vector tree(5, vector(9, vector{-1, -1}));
        int res = 0;
        for (const int t: nums) {
            // 深度
            const int d = t / 100;
            // 位置
            const int p = t % 100 / 10;
            // 节点值
            const int v = t % 10;
            // [出现次数,节点值] = [0,v]
            // 设置为0是因为后面用1的话会重复计算，因为后面需要累加
            tree[d][p] = {0, v};
        }
        // 从最底层开始
        for (int i = 4; i >= 1; --i) {
            // 遍历每个节点
            for (int j = 1; j <= 8; ++j) {
                // 如果是负数，表示空，跳过
                if (tree[i][j][0] < 0) {
                    continue;
                }
                // 如果是0，赋值成1
                if (tree[i][j][0] == 0) {
                    tree[i][j][0] = 1;
                }
                // 计算贡献，出现次数 * 节点值
                res += tree[i][j][0] * tree[i][j][1];
                // 父节点的出现次数加上当前节点的出现次数，相当于是计算路径经过次数
                tree[i - 1][(j + 1) >> 1][0] += tree[i][j][0];
            }
        }
        return res;
    }
};

5.4 Java版本

5.4.1 深搜法

import java.util.*;

public class Solution {
    private int res = 0;

    private void dfs(TreeNode node, int cur) {
        if (node == null) {
            return;
        }
        cur += node.val;
        if (node.left == null && node.right == null) {
            res += cur;
            return;
        }
        dfs(node.left, cur);
        dfs(node.right, cur);
    }

    public int pathSum(int[] nums) {
        TreeNode[][] tree = new TreeNode[5][9];
        TreeNode root = new TreeNode(nums[0] % 10);
        tree[1][1] = root;
        int n = nums.length;
        for (int i = 1; i < n; i++) {
            int d = nums[i] / 100;
            int p = nums[i] % 100 / 10;
            int v = nums[i] % 10;
            TreeNode node = new TreeNode(v);
            if ((p & 1) == 1) {
                tree[d - 1][(p + 1) >> 1].left = node;
            } else {
                tree[d - 1][(p + 1) >> 1].right = node;
            }
            tree[d][p] = node;
        }
        dfs(root, 0);
        return res;
    }
}

5.4.2 贡献法

import java.util.*;

public class Solution {
    public int pathSum(int[] nums) {
        int[][][] tree = new int[5][9][2];
        for (int[][] t : tree) {
            Arrays.fill(t, new int[]{-1, -1});
        }
        for (int t : nums) {
            tree[t / 100][t % 100 / 10] = new int[]{0, t % 10};
        }
        int res = 0;
        for (int i = 4; i >= 1; i--) {
            for (int j = 1; j <= 8; j++) {
                if (tree[i][j][0] < 0) {
                    continue;
                }
                if (tree[i][j][0] == 0) {
                    tree[i][j][0] = 1;
                }
                res += tree[i][j][0] * tree[i][j][1];
                tree[i - 1][(j + 1) >> 1][0] += tree[i][j][0];
            }
        }
        return res;
    }
}

5.5 Go版本

5.5.1 深搜法

func pathSum(nums []int) int {
	tree, res := make([][]*TreeNode, 5), 0
	for i := range tree {
		tree[i] = make([]*TreeNode, 9)
	}
	root := &TreeNode{Val: nums[0] % 10}
	tree[1][1] = root
	for i, n := 1, len(nums); i < n; i++ {
		d, p, v := nums[i]/100, nums[i]%100/10, nums[i]%10
		node := &TreeNode{Val: v}
		if p&1 == 1 {
			tree[d-1][(p+1)>>1].Left = node
		} else {
			tree[d-1][(p+1)>>1].Right = node
		}
		tree[d][p] = node
	}
	var dfs func(*TreeNode, int)
	dfs = func(node *TreeNode, cur int) {
		if node == nil {
			return
		}
		cur += node.Val
		if node.Left == nil && node.Right == nil {
			res += cur
			return
		}
		dfs(node.Left, cur)
		dfs(node.Right, cur)
	}
	dfs(root, 0)
	return res
}

5.5.2 贡献法

func pathSum(nums []int) int {
	tree, res := make([][][]int, 5), 0
	for i := range tree {
		tree[i] = make([][]int, 9)
		for j := range tree[i] {
			tree[i][j] = []int{-1, -1}
		}
	}
	for _, t := range nums {
		tree[t/100][t%100/10] = []int{0, t % 10}
	}
	for i := 4; i >= 1; i-- {
		for j := 1; j <= 8; j++ {
			if tree[i][j][0] < 0 {
				continue
			}
			if tree[i][j][0] == 0 {
				tree[i][j][0] = 1
			}
			res += tree[i][j][0] * tree[i][j][1]
			tree[i-1][(j+1)>>1][0] += tree[i][j][0]
		}
	}
	return res
}

6 总结

本文介绍了路径总和系列四道题的解法，其中1和2比较简单直接DFS可以解决，3主要用到了前缀和，4就是构建树。

路径总和3的做法，本质上和560题是一样的，有兴趣的读者可以看看。

7 附录

• 路径总和1
• 路径总和2
• 路径总和3
• 路径总和4