题目
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(k 从 1 开始计数)。
数据范围
java
树中的节点数为 n 。
1 <= k <= n <= 10^4^
0 <= Node.val <= 10^4^测试用例
示例1
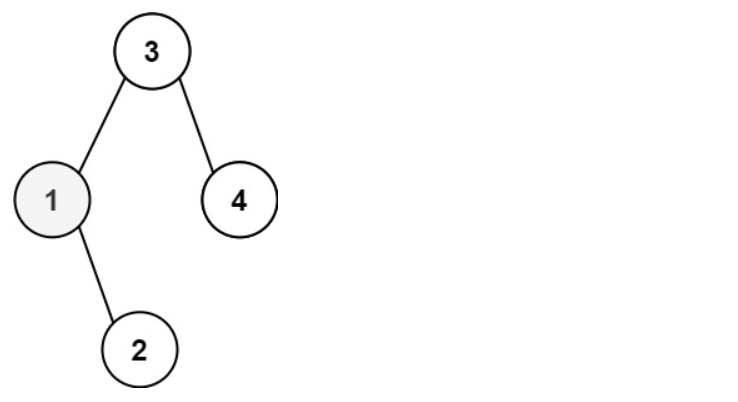
java
输入:root = [3,1,4,null,2], k = 1
输出:1示例2
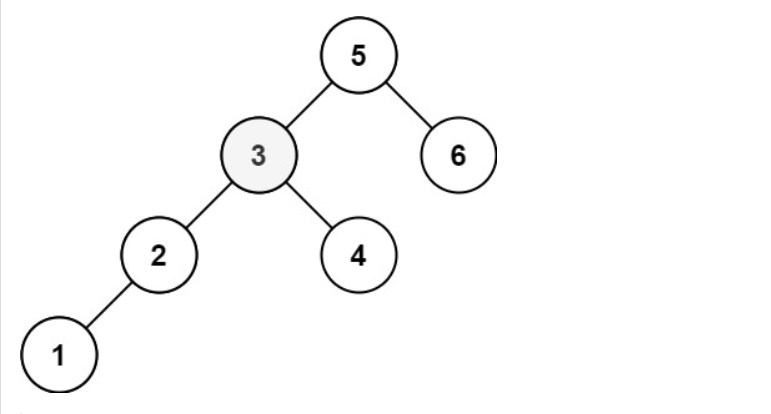
java
输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3题解1(中序遍历,时间复杂度O(H+k),空间O(H),H为树高)
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int kthSmallest(TreeNode root, int k) {
// 使用双端队列 ArrayDeque 作为栈(Stack)来模拟递归调用
// 栈用于存储待处理的节点,以便稍后回溯
Deque<TreeNode> stack = new ArrayDeque<>();
// 循环条件:
// 1. root != null: 还有节点可以往左深入
// 2. !stack.isEmpty(): 还有节点在栈中等待被访问
while (root != null || !stack.isEmpty()) {
// 步骤 1: 尽可能向左走 (Go Left)
// 将路径上的所有节点压入栈中,直到最左下角的节点
// 这一步是为了找到当前子树中"最小"的节点
while (root != null) {
stack.push(root);
root = root.left;
}
// 步骤 2: 处理当前节点 (Visit Root)
// 此时 root 为 null,说明左边没有更小的了
// 弹出栈顶元素,这就是当前未访问节点中最小的一个
root = stack.poll();
// 每弹出一个节点,意味着找到了第 k 大的一个"名额"
k--;
// 如果 k 减为 0,说明当前弹出的这个节点就是第 k 小的元素
if (k == 0) {
break题解2(记录子树节点数,时空复杂度O(N))
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int kthSmallest(TreeNode root, int k) {
// 初始化辅助类 BST,预处理树的节点数量
BST bst = new BST(root);
// 获取第 K 小的值
return bst.getKmin(k);
}
// 内部辅助类,用于封装根节点和节点计数缓存
class BST {
TreeNode root;
// 使用哈希表缓存每个节点作为根的子树包含的节点总数
// Key: 节点对象, Value: 以该节点为根的子树节点总数
HashMap<TreeNode, Integer> map;
public BST(TreeNode root) {
this.root = root;
map = new HashMap<TreeNode, Integer>();
// 构造时立即遍历全树,计算并缓存所有子树的节点数
countNode(root);
}
// 核心方法:查找第 k 小的元素
public int getKmin(int k) {
TreeNode node = root;
// 利用 BST 性质进行类似于二分查找的搜索
while (node != null) {
// 获取左子树的节点数量 (num)
// 注意:原代码这里调用 countNode 会重新递归计算,效率较低,建议改为查表 (map.get)
int num = countNode(node.left);
// 逻辑判断:
// 二叉搜索树中,左子树所有节点 < 当前节点 < 右子树所有节点
if (num < k - 1) {
// 情况 1: 左子树节点数(num) 不够 k-1 个
// 说明第 k 小的数不在左边,也不在当前节点(是第 num+1 小),而在右子树中
// 我们需要跳过左子树的所有节点(num个)加上当前节点(1个)
// 所以在右子树中寻找第 (k - num - 1) 小的元素
k = k - num - 1;
node = node.right;
} else if (num == k - 1) {
// 情况 2: 左子树刚好有 k-1 个节点
// 那么当前节点正是第 (k-1) + 1 = k 小的元素
break;
} else {
// 情况 3: 左子树节点数超过了 k-1 个 (num > k-1)
// 说明第 k 小的元素一定在左子树内部
node = node.left;
}
}
return node.val;
}
// 递归计算子树节点数量,并存入 map
public int countNode(TreeNode node) {
if (node == null) {
return 0;
}
// 当前节点数 = 1 + 左子树节点数 + 右子树节点数
// 计算结果存入 map 以便后续查询
map.put(node, 1 + countNode(node.left) + countNode(node.right));
return map.get(node);
}
// 辅助方法:直接从 map 获取节点数,避免空指针异常
public int getcount(TreeNode root) {
return map.getOrDefault(root, 0);
}
}
}思路
这道题第一个方法思路比较简单,就是利用了二叉搜索树的中序遍历是升序这个特性,就能完成解答,性能也很优,第二种解法是则是从树的角度出发,具体来说分为如下三种情况。
如果 node 的左子树的结点数 left 小于 k−1,则第 k 小的元素一定在 node 的右子树中,令 node 等于其的右子结点,k等于 k−left−1,并继续搜索;
如果 node 的左子树的结点数 left 等于 k−1,则第 k 小的元素即为 node,结束搜索并返回 node 即可;
如果 node 的左子树的结点数 left 大于 k−1,则第 k 小的元素一定在 node的左子树中,令 node 等于其左子结点,并继续搜索。