在机器学习和优化领域,我们常常面临这样的困境:如何在浩瀚的参数空间中找到最优解?传统方法如网格搜索计算成本高昂,而遗传算法又过于复杂。今天,让我们认识一种既简单又高效的替代方案------粒子群算法,它用群体智能的智慧,为优化问题提供了优雅的解决方案。
一、算法起源
粒子群优化算法(PSO)是一种进化计算技术,灵感来源于鸟群觅食和鱼群游动等自然群体行为。最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。
 鸟群觅食行为
鸟群觅食行为
想象一片广阔的麦田,散落着一些未被收割的麦穗("最优解")。一群麻雀("粒子群")急需找到这些麦穗来储备过冬的粮食。

- 麻雀不知道麦穗的具体位置,但它们飞过的地方,能清晰地看到地面是否有麦粒(评估当前位置的适应度)。
- 麻雀之间有一套高效的沟通方式,每只麻雀在飞行搜索时,其行为由三种关键因素决定:
- 惯性 → 保持自己当前的飞行方向和速度,不会突然掉头。(保持原有状态)
- 个体认知 → "我记得我之前在东边那个田埂旁找到过几粒很大的麦穗,那个地方我得记着。"(个体最优解 pbest)
- 社会学习 → 我听到鸟群中叽叽喳喳,似乎都在说北边那块洼地发现了大量的麦穗堆!(群体最优解 gbest)
- 麻雀的每一次振翅都是决策,它既不会完全飞向自己记忆中的老地方(可能已经被吃光了),也不会盲目地直接冲向北边的洼地(可能距离太远),而是在每一次飞行中,动态地调整方向:大部分方向还是延续自己之前的飞行路线(惯性)。但会稍微偏向自己记忆中最好的那个位置(个体认知)。同时,更明显地偏向于群体公认的最佳位置(社会学习)。
- 最终结果:起初,麻雀群四散纷飞,一片混乱。但很快,通过这种持续分享"我见过的最好地点"的简单规则,一些原本在边缘的麻雀开始被"吸引"到更有希望的区域。
二、基本思想
01算法定义
粒子群算法,也称粒子群优化算法或鸟群觅食算法(Particle Swarm Optimization,PSO)。是近年来由J. Kennedy和R. C. Eberhart等开发的一种新的进化算法。PSO 算法属于进化算法的一种,和模拟退火算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质,但它比遗传算法规则更为简单,它没有遗传算法的"交叉"和"变异"操作,它通过追随当前搜索到的最优值来寻找全局最优。
02核心思想
群体中的个体(即"粒子")虽然缺乏全局视角,但通过与邻居共享信息,可以共同找到食物或安全区域。在PSO中,每个粒子代表搜索空间中的一个候选解,粒子的位置对应于问题的解,粒子的适应度则由目标函数值决定。PSO将每一个候选解看作一个"粒子",在搜索空间中飞行寻找最优解。每个粒子根据自身经验(个体最优)和群体经验(全局最优)动态调整位置和速度,实现对搜索空间的探索与利用。
总结来说,核心思想就是:通过个体(粒子)间的社会信息共享(个体经验与群体经验)实现对非线性函数的优化。
03粒子数学表征与寻优机制
(1)每个粒子有两个主要属性:
- 位置(Position):表示当前的解。粒子的当前位置就是它认为的潜在最优解。
- 速度(Velocity):决定了粒子的移动方向和速度。通过调整速度,粒子可以在解空间中探索新的位置。
(2)每个粒子同时受到两种"引导":
- 个体最优(Personal Best,pbest):粒子自身历史上找到的最好位置,体现其个体记忆与学习能力;
- 群体最优(Global Best,gbest):全体粒子中当前找到的最好位置,体现群体信息共享与协作。每一代中,粒子根据惯性、个体最优引力和群体最优引力,更新自己的速度与位置。数学上,通过加入随机性因子模拟个体的探索多样性,防止早期陷入局部最优。同时,惯性权重控制全局搜索与局部搜索的平衡:较大的惯性值有利于保持探索能力,较小的值促进收敛。
04算法优势
PSO结合了进化计算和群体智能的特点,具有以下优势:
- 简单性:仅需位置、速度、个体最优和全局最优(四个核心变量)。
- 低计算成本:无需复杂数学运算,适用于高维优化问题。
- 广泛适用性:成功应用于神经网络训练、函数优化等领域。
三、算法原理
1、算法流程图
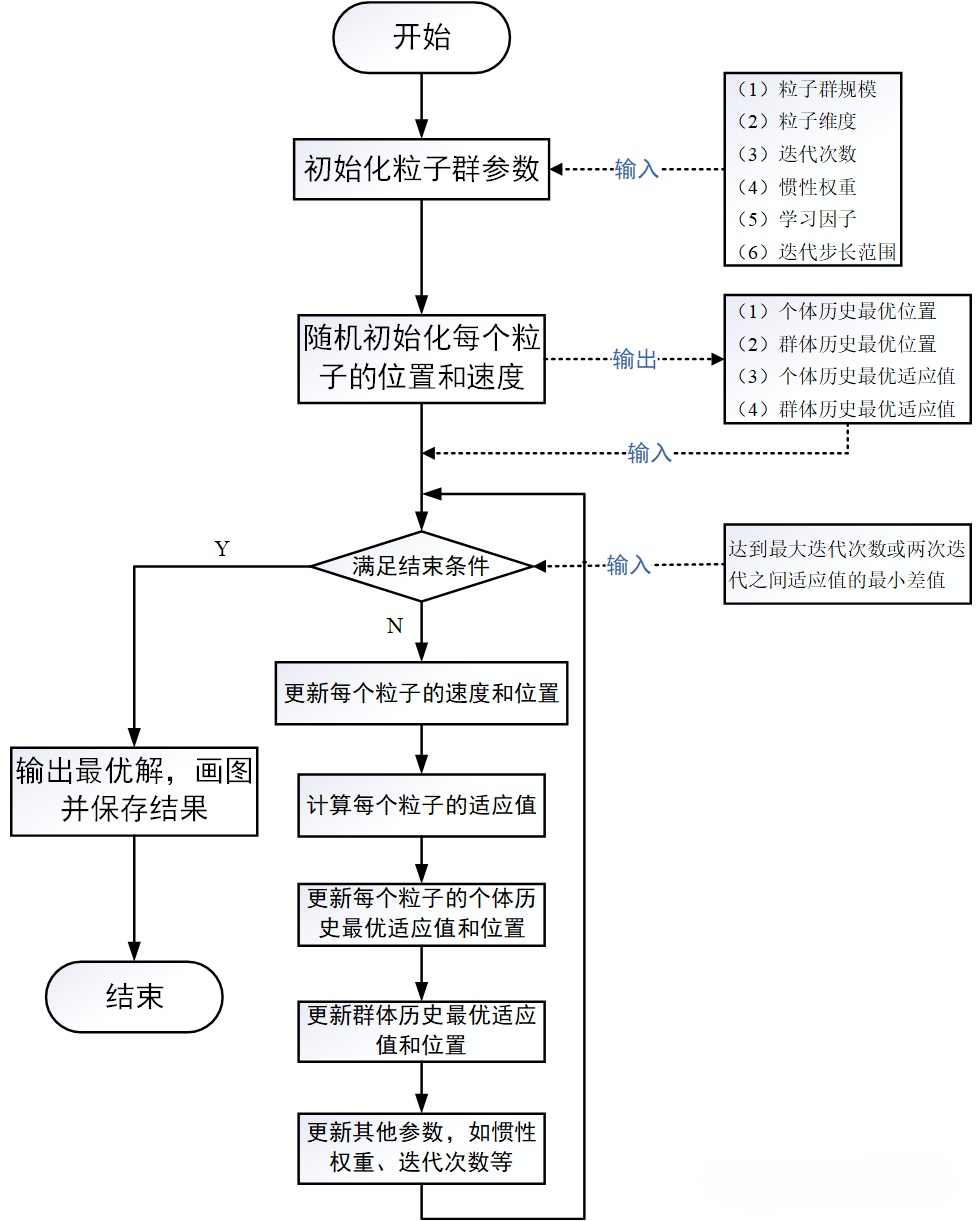
2、基本思路
- 01初始化粒子群
随机生成一群粒子,每个粒子代表解空间中的一个潜在解。每个粒子具有位置(表示解的坐标)和速度(控制移动方向和步长)两个属性。
- 02评估适应度
根据目标函数计算每个粒子的适应度值,用于衡量解的优劣。适应度值越优,说明粒子越接近最优解。
- 03更新个体最优和全局最优
个体最优(pbest):记录每个粒子自身历史上的最优位置及对应的适应度值。若当前粒子的适应度优于历史最优,则更新个体最优。
全局最优(gbest):从所有粒子的个体最优中选取最优者,作为当前全局最优位置。
- 04更新粒子速度和位置
根据以下公式迭代更新粒子的速度和位置:
粒子的新速度 = 惯性(保持原方向) + 认知(飞向自己的最佳) + 社会(飞向群体的最佳)
新位置 = 原位置 + 新速度
- 05迭代终止条件
重复上述步骤,直到满足终止条件,如达到最大迭代次数或全局最优值的变化小于设定阈值。通过不断迭代,粒子群在解空间中动态调整位置,逐步向最优解靠近。
3、数学模型
定义第 i 个粒子在 d 维搜索空间中的信息:
位置:
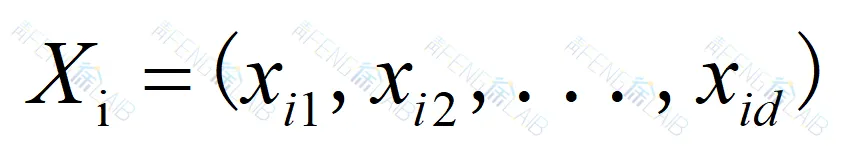
速度:
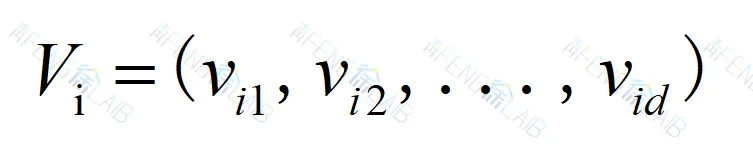
个体历史最佳位置:
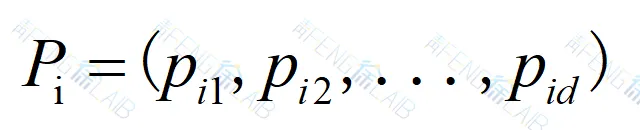
群体历史最佳位置:
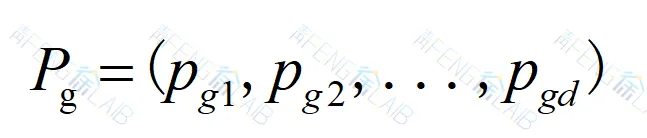
在每一次迭代中(从时刻 k 到 k +1),每个粒子的速度和位置按以下公式进行更新:
(1)速度更新公式
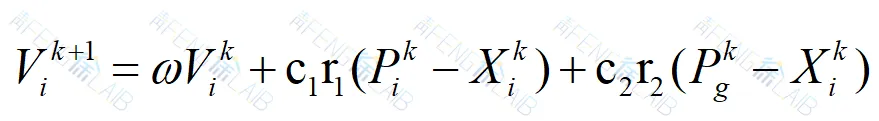
(2)位置更新公式
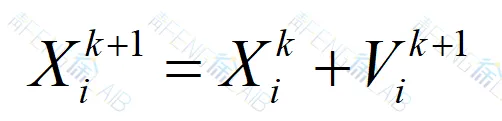
表1 参数含义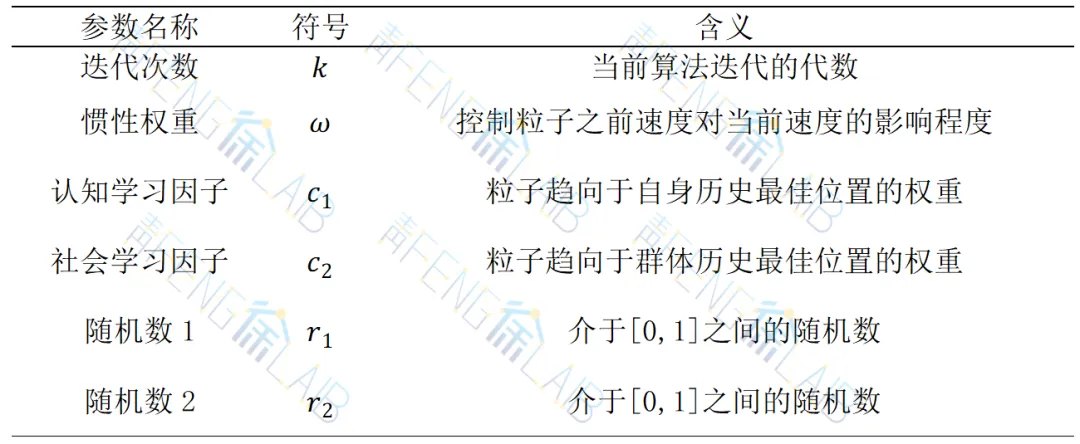
四、应用案例
学会粒子群算法的基本原理后,接下来我们就从函数优化与路径优化两大应用入手,通过4个经典案例拆解粒子群算法的实战用法!小编会同步展示解题代码, 小伙伴们赶紧关注【运筹说】公众号,在后台回复 "粒子群算法",就能免费获取完整代码啦!
(一)函数优化
粒子群算法(PSO)凭借群体协作与高效寻优特性,在函数优化领域应用广泛。
其核心是通过粒子表征函数解空间的可行解,借助位置 - 速度更新规则与个体 / 全局最优引导,实现对目标函数的高效搜索。
该算法适用于连续 / 离散、单目标 / 多目标函数优化,可处理非线性、非凸、高维及带约束的复杂函数场景,如工程设计中的参数优化、数据拟合、机器学习模型超参数调优、信号处理中的滤波参数优化等。
相较于传统优化方法,PSO 收敛速度快、鲁棒性强,能有效平衡全局探索与局部开发,大幅降低复杂函数寻优的计算成本,是函数优化领域的经典群智能优化工具。
接下来,小编将分别介绍算法在一元函数优化与二元函数优化中的展现的强大的算法优势。
一元函数优化
1、问题描述
在该例中,想要优化的一元函数为
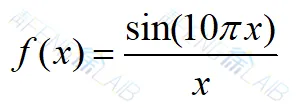
当 x 范围在[1,2],寻找它的极大值。
2、PSO解题思路
- 粒子表示:每个粒子的位置 x 是一个实数,代表解空间中的一个候选解,速度 v 控制 x 的更新步长和方向。
- 适应度函数:直接使用 f(x) 作为适应度值,目标是最大化 f(x)。
- 初始化:随机生成一群粒子,位置 x 均匀分布在[1,2]内,速度 v 初始化为小随机值。
- 更新策略:每次迭代中,粒子根据速度更新公式(考虑惯性、个体认知和社会学习)调整速度,并更新位置x = x + v;位置需约束在[1,2]范围内,若越界则采用边界处理(如反射或截断)。
- 终止条件:当达到最大迭代次数或全局最优解变化小于阈值时停止。
- 关键点:PSO通过粒子间信息共享,快速收敛到函数峰值附近,避免局部极值。
3、简单代码
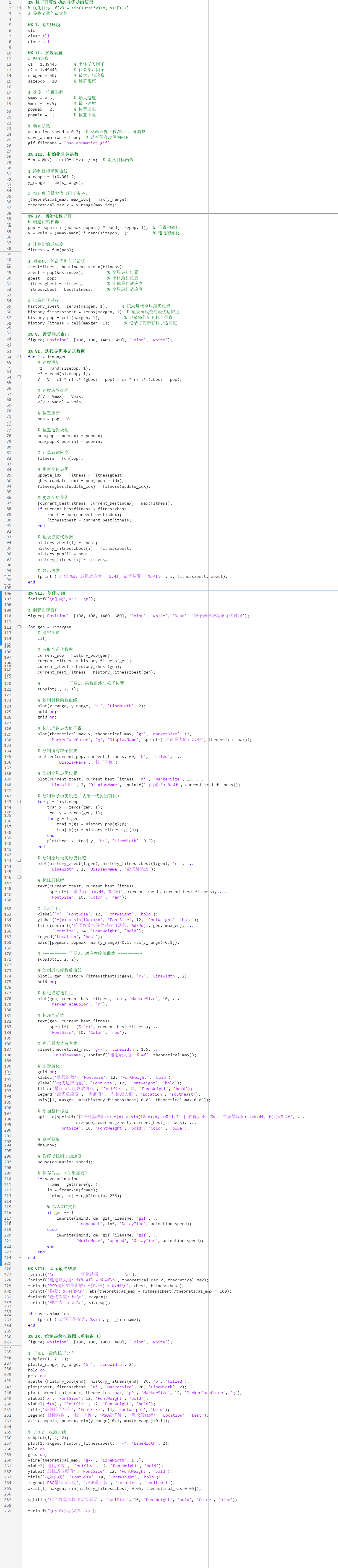
4、结果展示
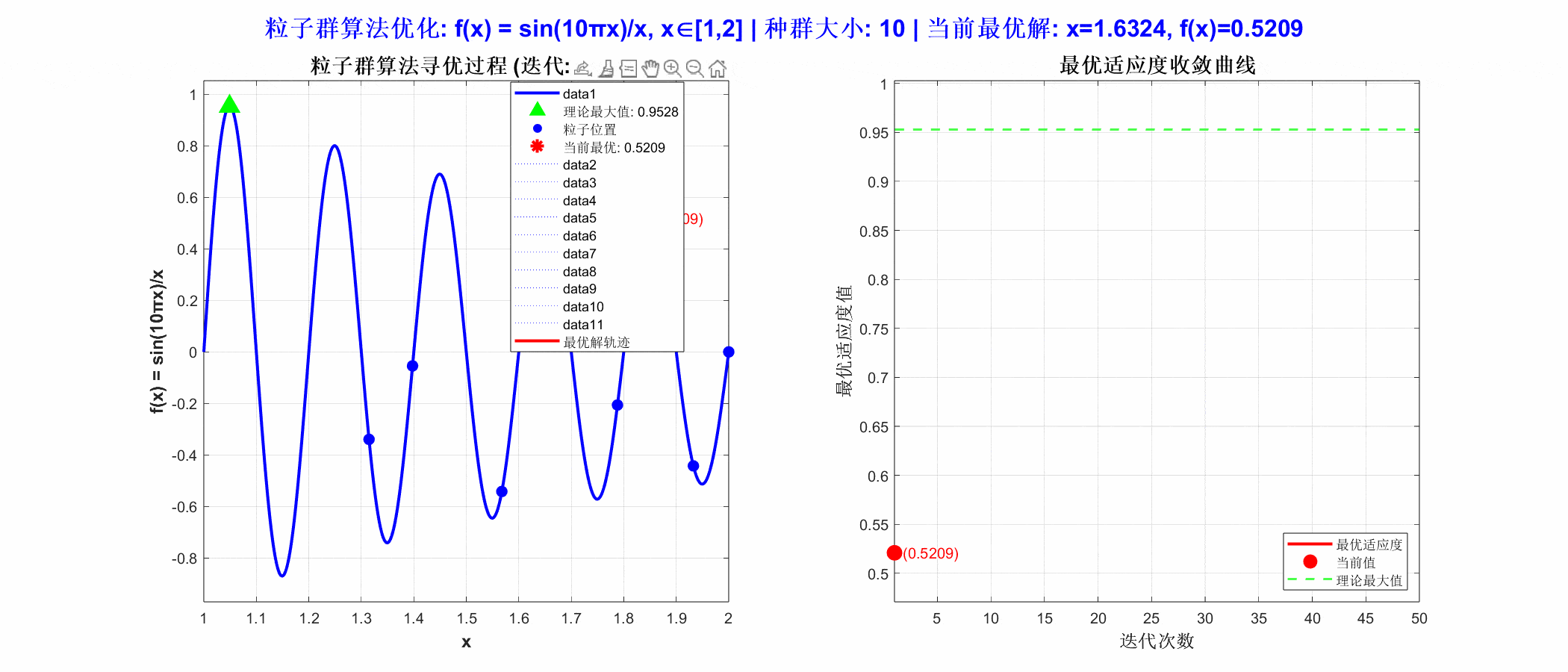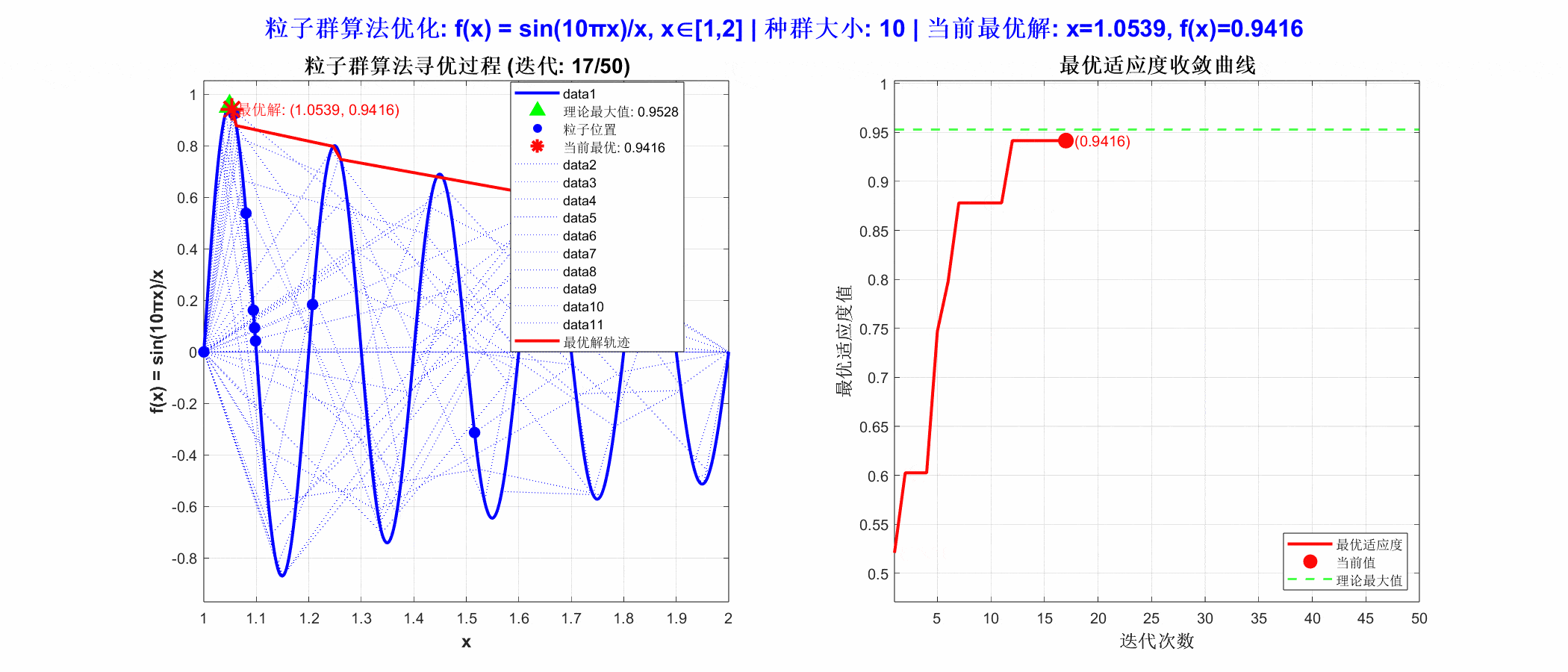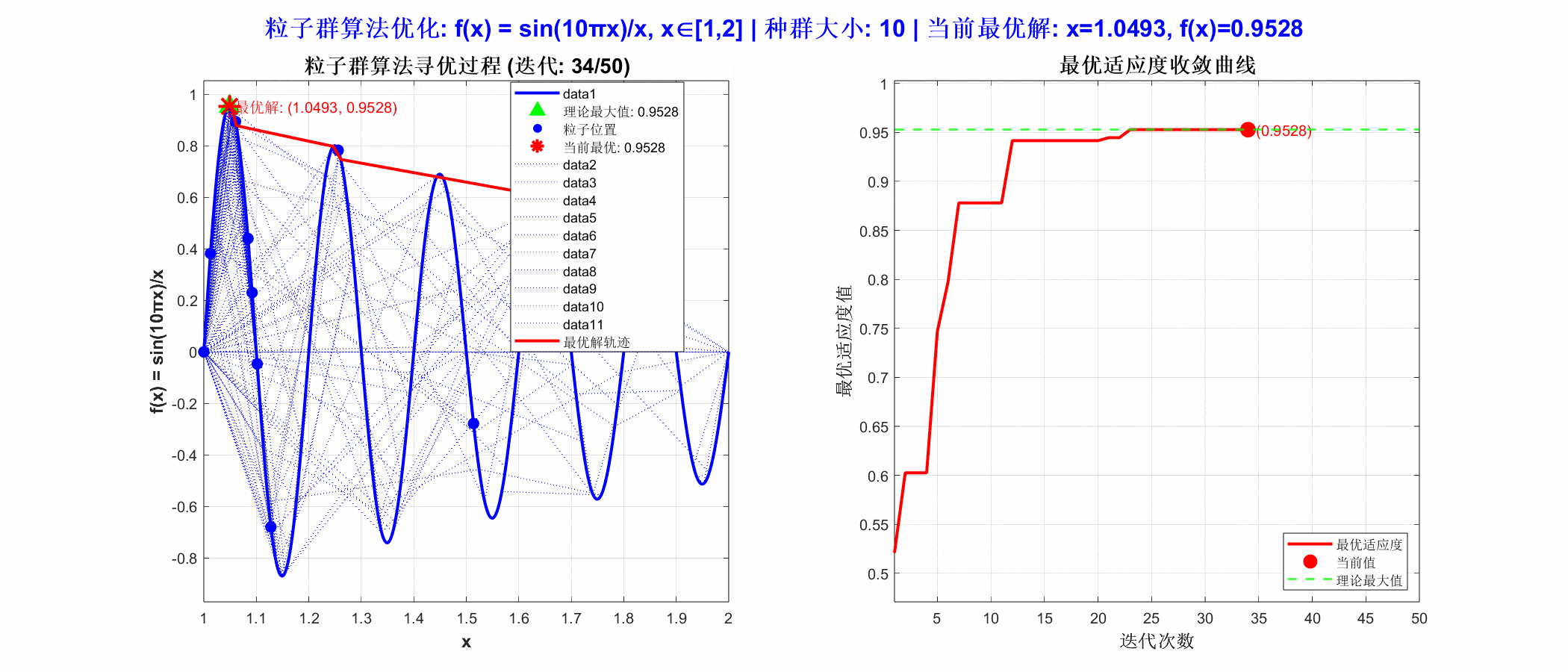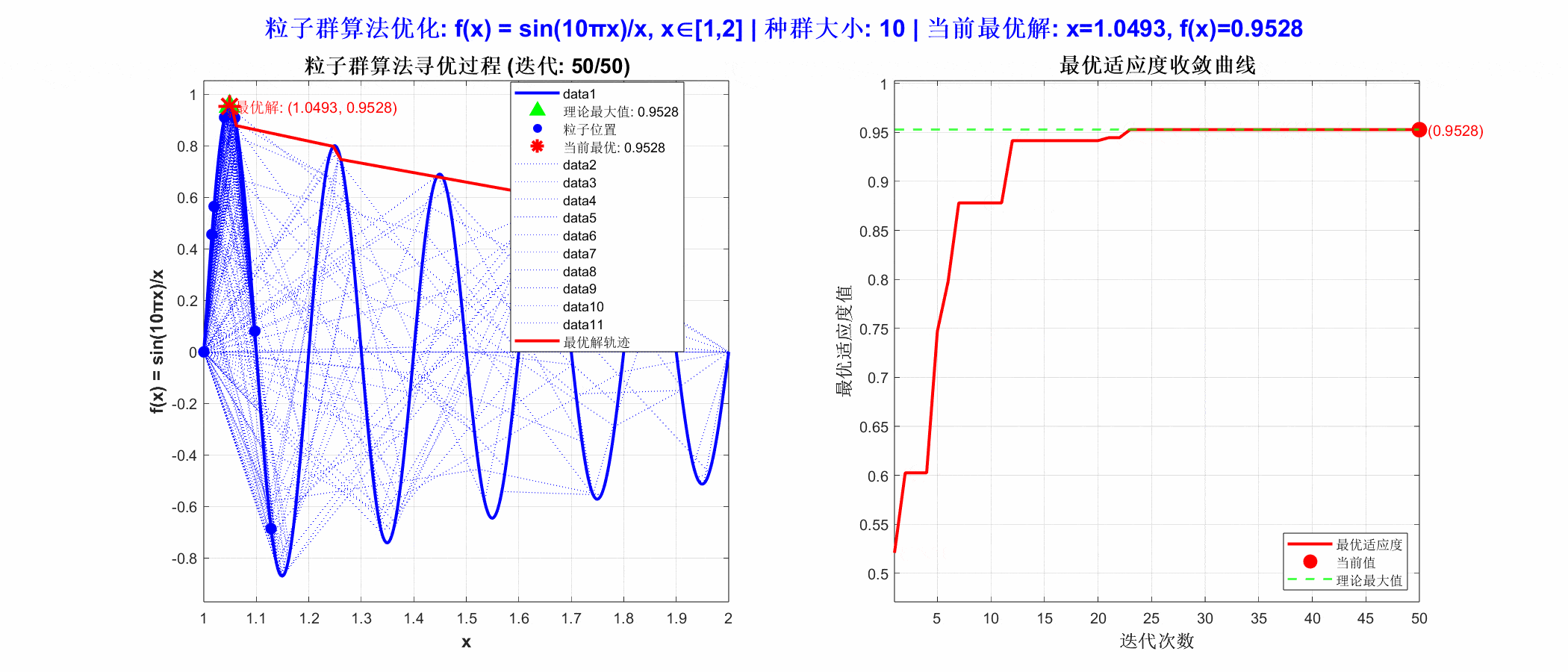
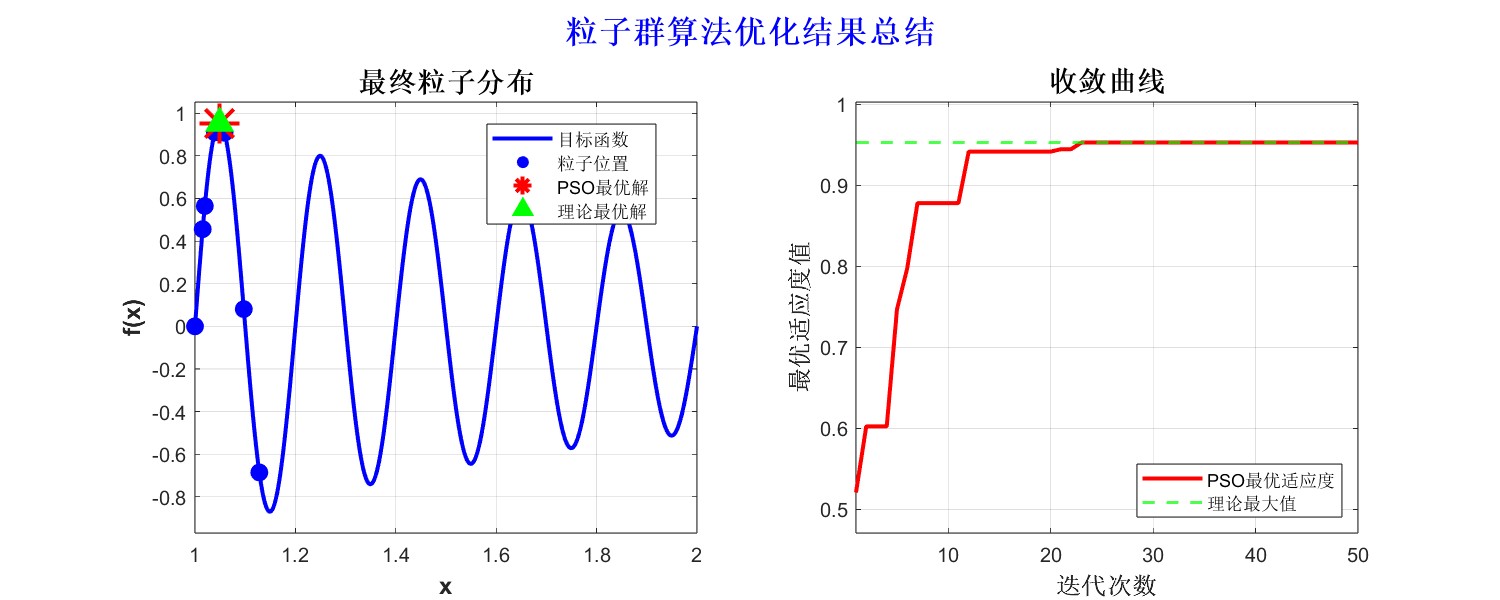

从运行结果可以看出,PSO算法在区间 [1, 2] 内找到了函数的最大值。粒子群在迭代过程中迅速向极值点 x =1.0493聚集,收敛速度快且稳定。这说明算法在处理一维连续优化问题时,具有良好的全局搜索与局部开发平衡能力,能有效避免陷入局部最优,适用于参数调优、曲线拟合等场景。
二元函数优化
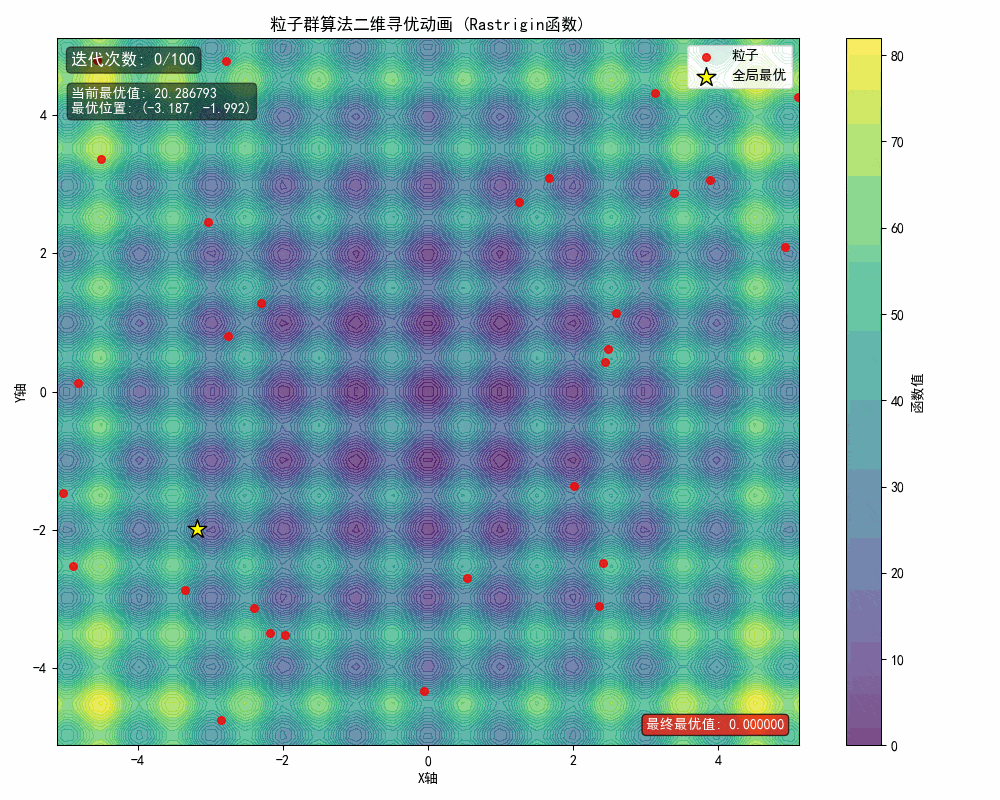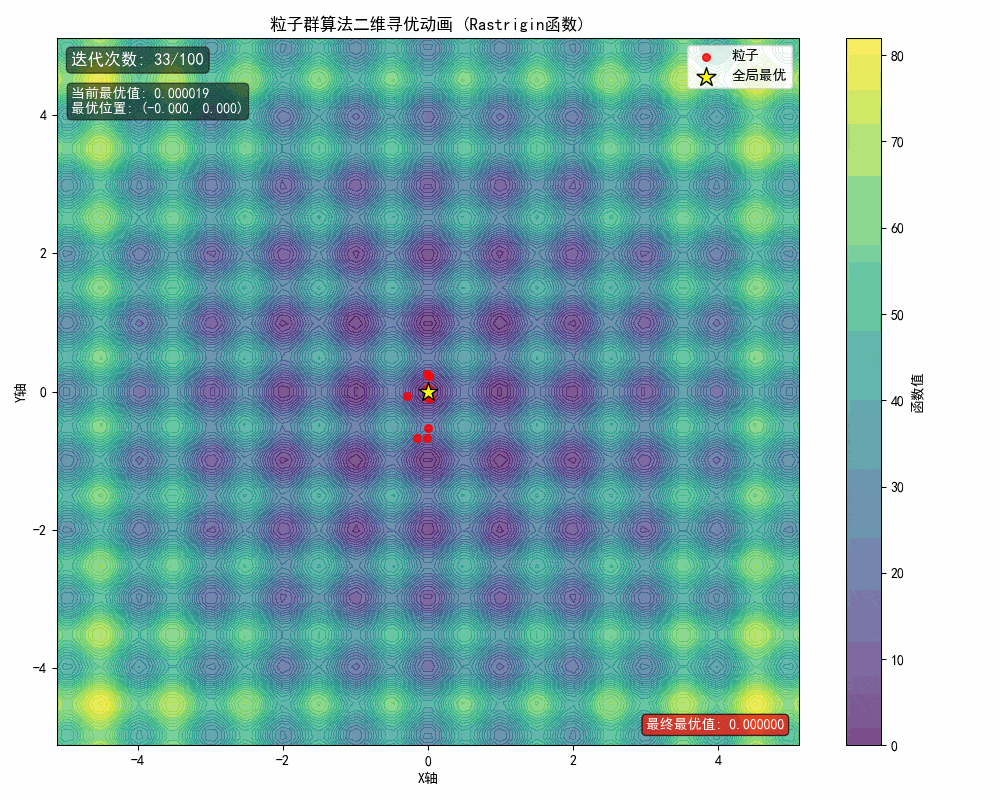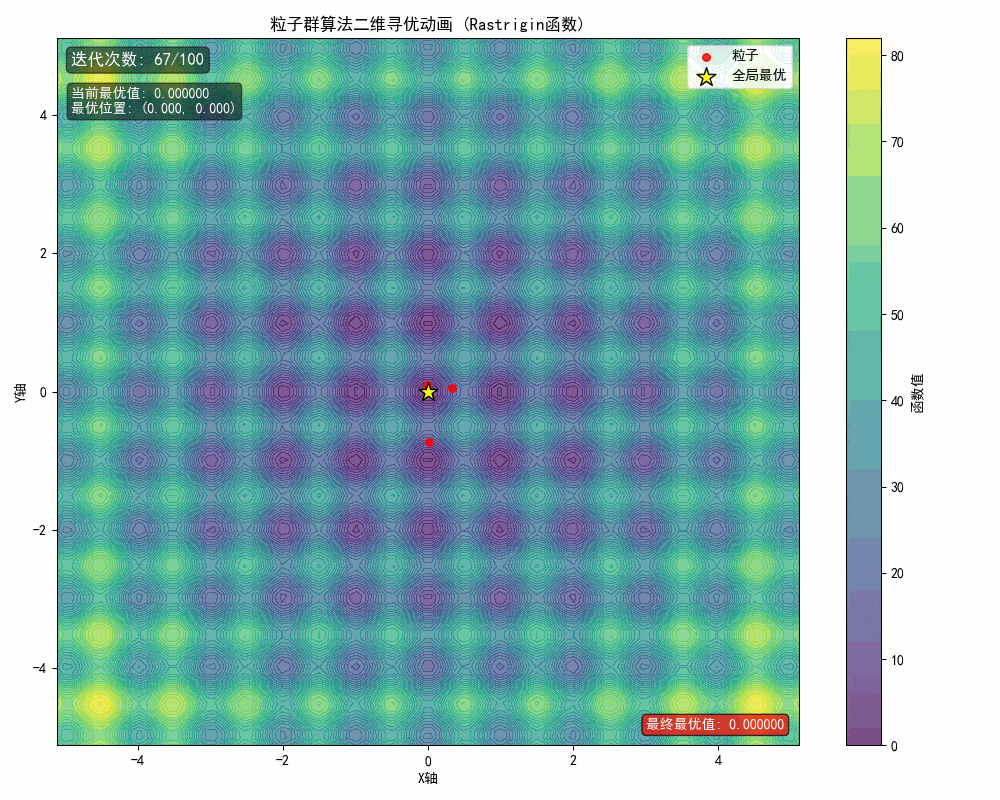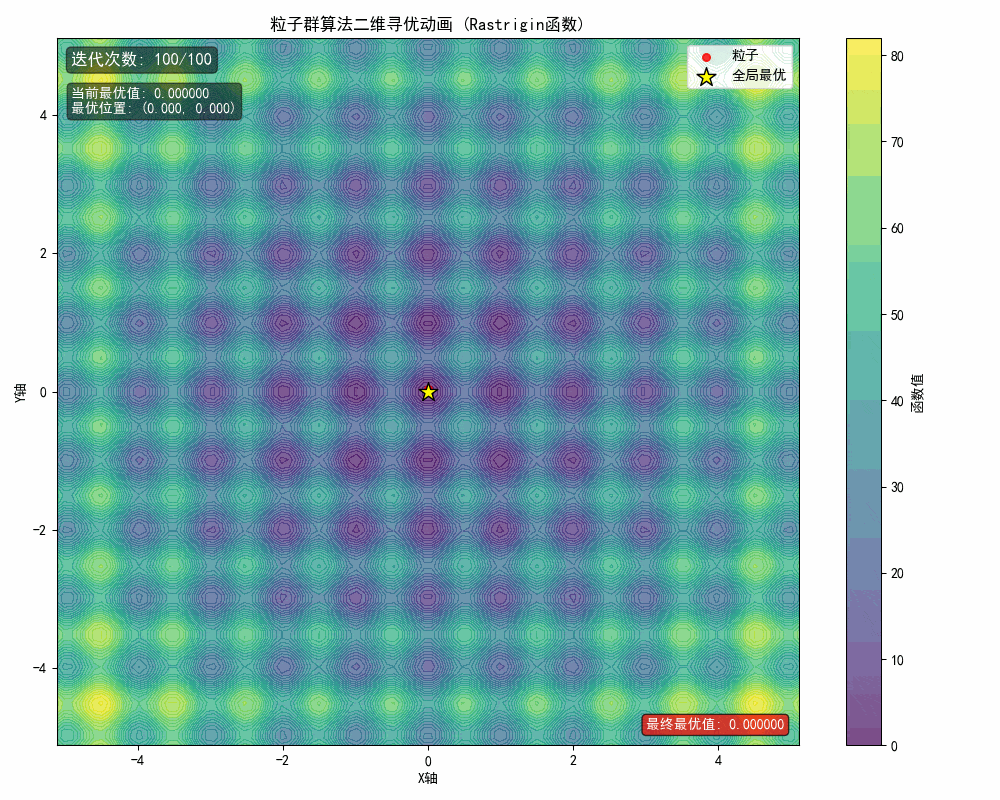
1、问题描述
在该例中,想要优化的一元函数为
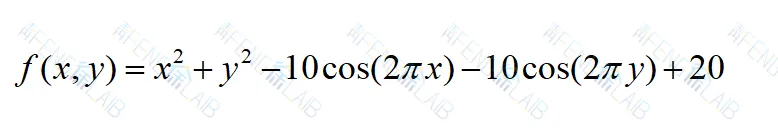
当 x 和 y 范围都在[-5,5],寻找它的极大值。
2、PSO解题思路
- 粒子表示:每个粒子的位置是一个二维向量(x,y),代表解空间中的一个候选解,速度也是二维向量。使用 f ( x,y)作为适应度值,目标是最大化 f ( x,y)。
- 适应度函数:使用 f ( x,y)作为适应度值,目标是最大化 f ( x,y)。
- 初始化:随机生成一群粒子,位置 x 均匀分布在[-5,5]*[-5,5]内,速度初始化为随机值。
- 更新策略:速度和位置更新使用二维扩展公式,确保每个维度独立更新;位置约束通过边界处理实现,防止粒子飞出定义域。
- 终止条件:类似一元函数优化,依赖迭代次数或收敛阈值。
- 关键点:PSO能有效处理二维搜索空间,通过社会学习引导粒子向全局最优点聚集。
3、简单代码

4、结果展示
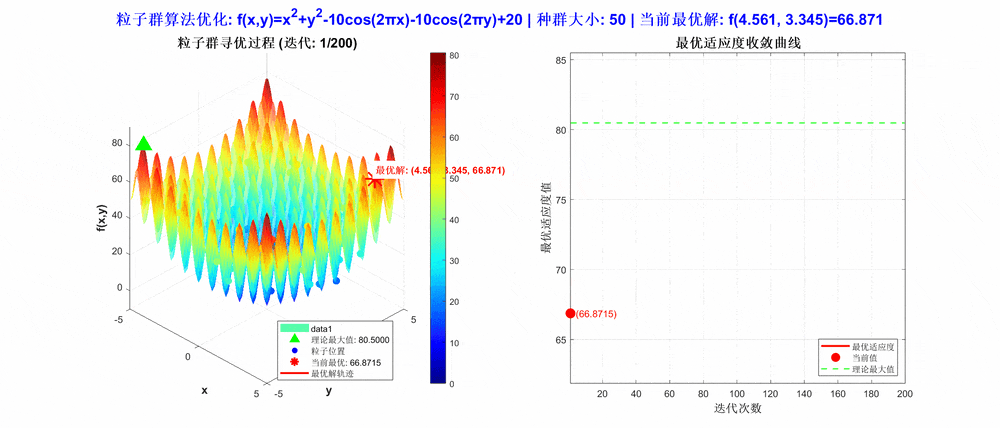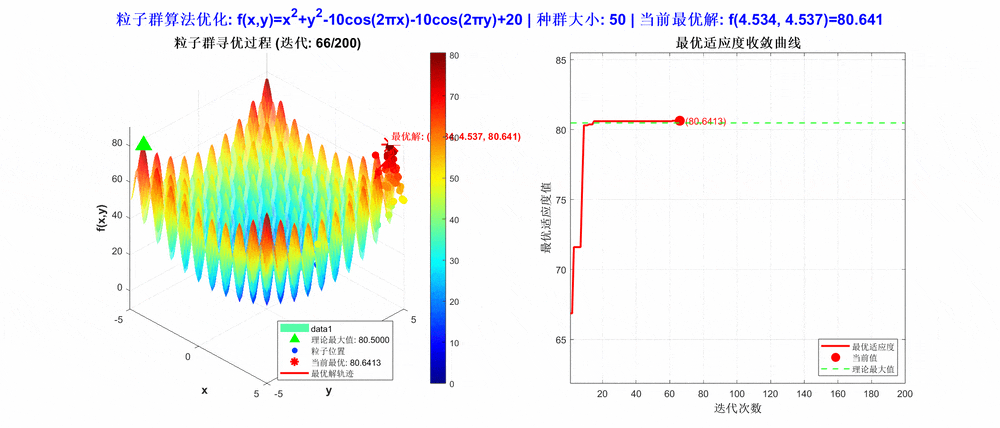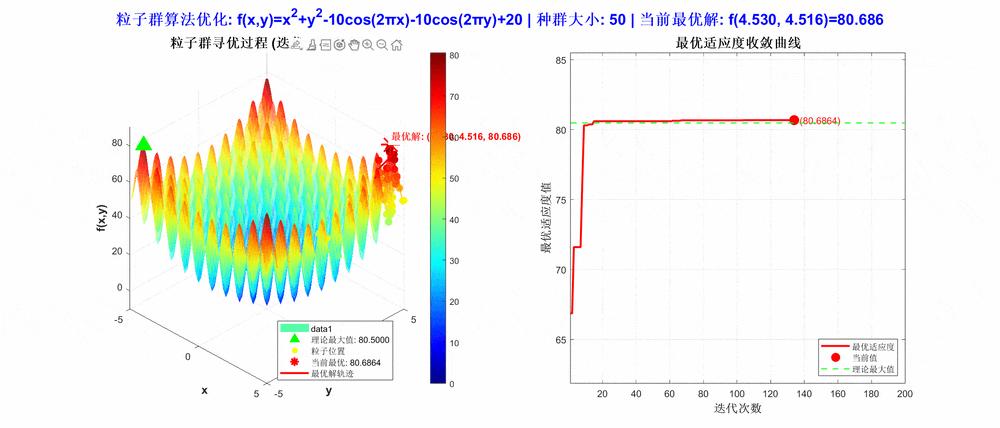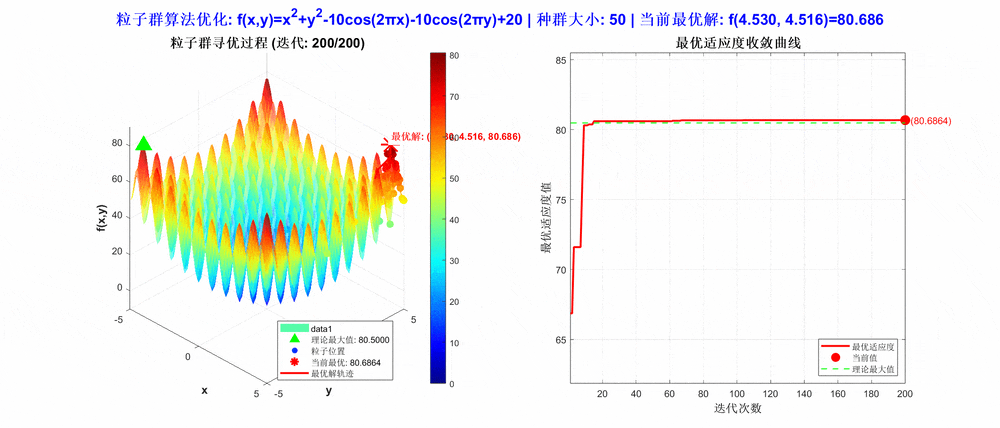
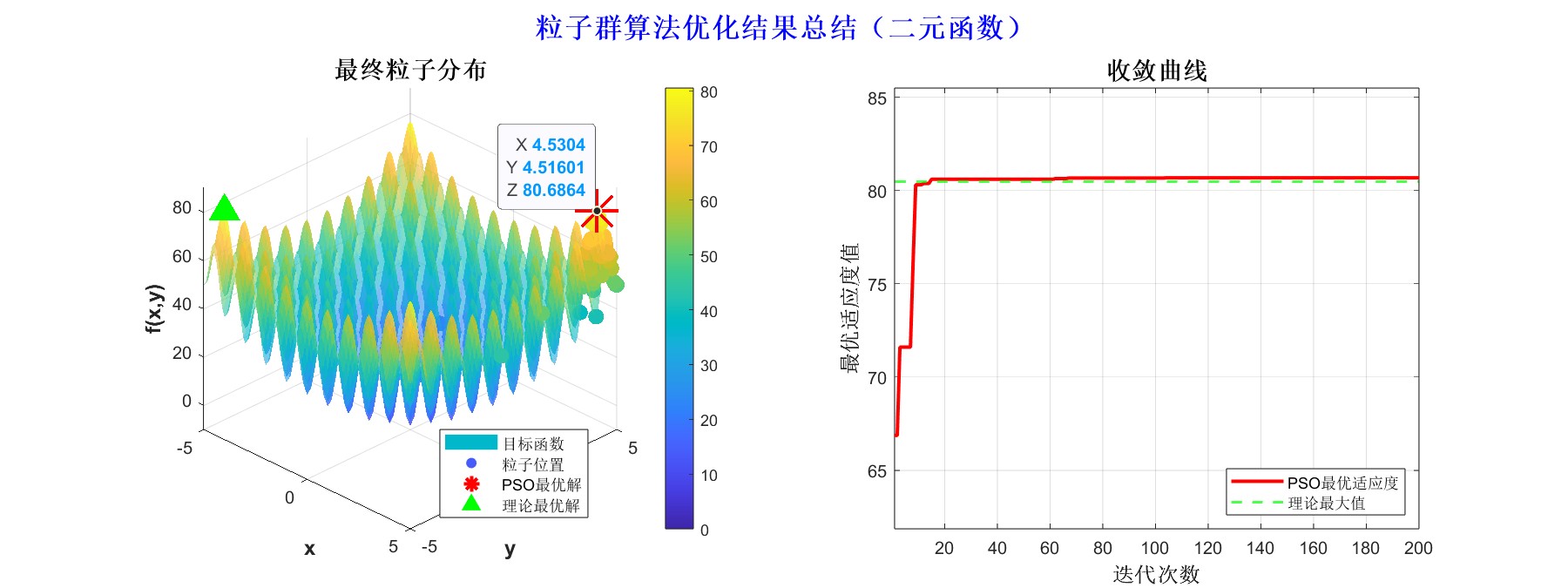
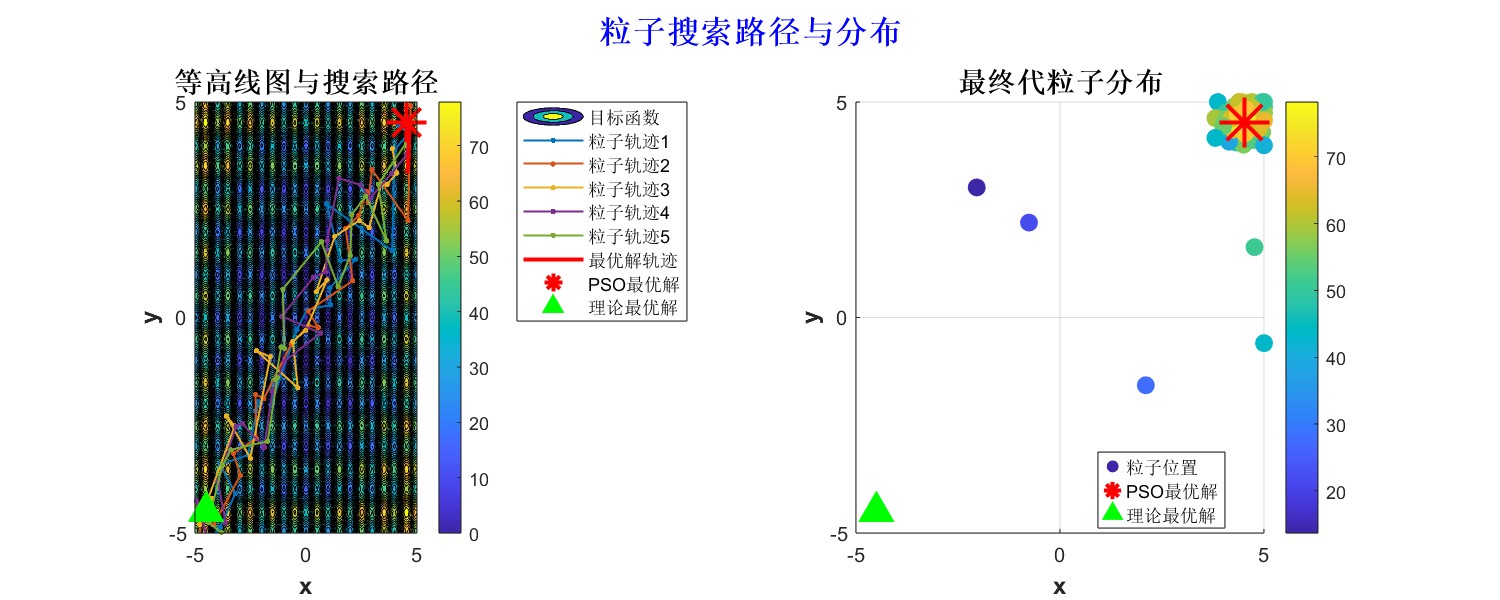

从运行结果可以看出,算法在定义域内成功定位到全局最大值点(4.530,-4.516),最大值为80.686。图像显示粒子在二维空间中逐渐向最优区域聚集,验证了PSO算法在高维非线性函数优化中的有效性。其社会学习机制使粒子能协同探索复杂解空间,适用于多参数优化、机器学习超参数调优等问题。
(二)路径优化
粒子群算法(PSO)凭借群体协作寻优与强鲁棒性,在路径规划领域应用广泛。其核心是将路径节点映射为粒子位置,以路径长度、避障代价、能耗等为适应度函数,通过粒子速度-位置更新规则及个体/全局最优引导,搜索最优路径。
该算法适用于机器人、无人机、物流配送等场景,可高效处理静态/动态环境、单/多智能体、带约束(避障、能耗限制)的路径规划问题。相较于传统方法,PSO收敛速度快、易处理高维路径空间,能有效平衡路径最优性与可行性,为复杂场景下的路径规划提供灵活高效的解决方案。
接下来,小编将分别介绍算法在单智能体路径规划与多智能体路径规划问题的优化中的展现的强大的算法优势。
单智能体路径规划
旅行商问题(Traveling Salesman Problem, TSP)是路径规划领域的经典 NP 难问题,核心目标是在给定城市集合及城市间距离的前提下,为旅行者规划一条访问所有城市仅一次且最终返回起点的最短闭环路径,是单智能体路径规划中 "全局最优路径搜索" 的典型研究载体。
1、问题描述
给定一个城市集合和每对城市之间的距离,要求找出访问每个城市一次并返回起点的最短路径。
在TSP问题中,PSO将每个解看作一个粒子,通过不断更新粒子的速度和位置来寻找最优解。
粒子表示:每个粒子表示一个可能的解,即一条路径。粒子的位置由路径中城市的排列顺序决定。
需要注意的是,在更新位置时要保证新生成的路径满足TSP问题的约束条件。
2、PSO解题思路
- 粒子表示:每个粒子表示一条路径,即城市的排列(如[3,1,4,2])。位置编码为离散序列,速度表示为交换序或概率向量。
- 适应度函数:路径总长度的倒数或负值(如 fitness = - 总距离),以最小化距离为目标。
- 初始化:随机生成多个合法路径作为粒子初始位置,速度初始化为零或小随机交换序。
- 更新策略:
- 速度更新:在离散PSO中,速度可定义为城市交换的概率或倾向;
- 位置更新:根据速度应用交换操作,生成新路径。例如,通过部分映射交叉(PMX)或交换子序列确保路径合法性。
- 终止条件:当最优路径不再改善或达到最大迭代次数时停止。
- 关键点:PSO需结合局部搜索(如2-opt)提升解质量,并确保路径满足TSP约束(每个城市只访问一次)。
3、简单代码

4、结果展示
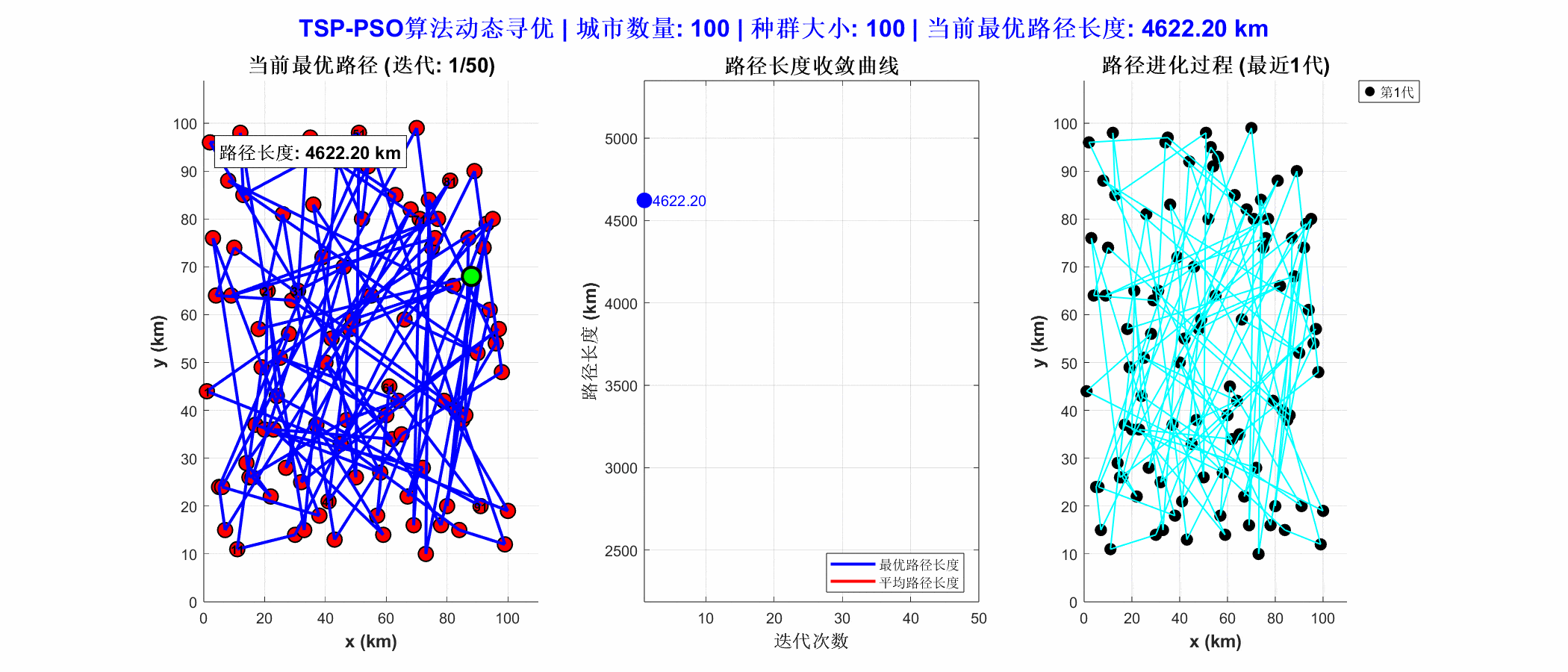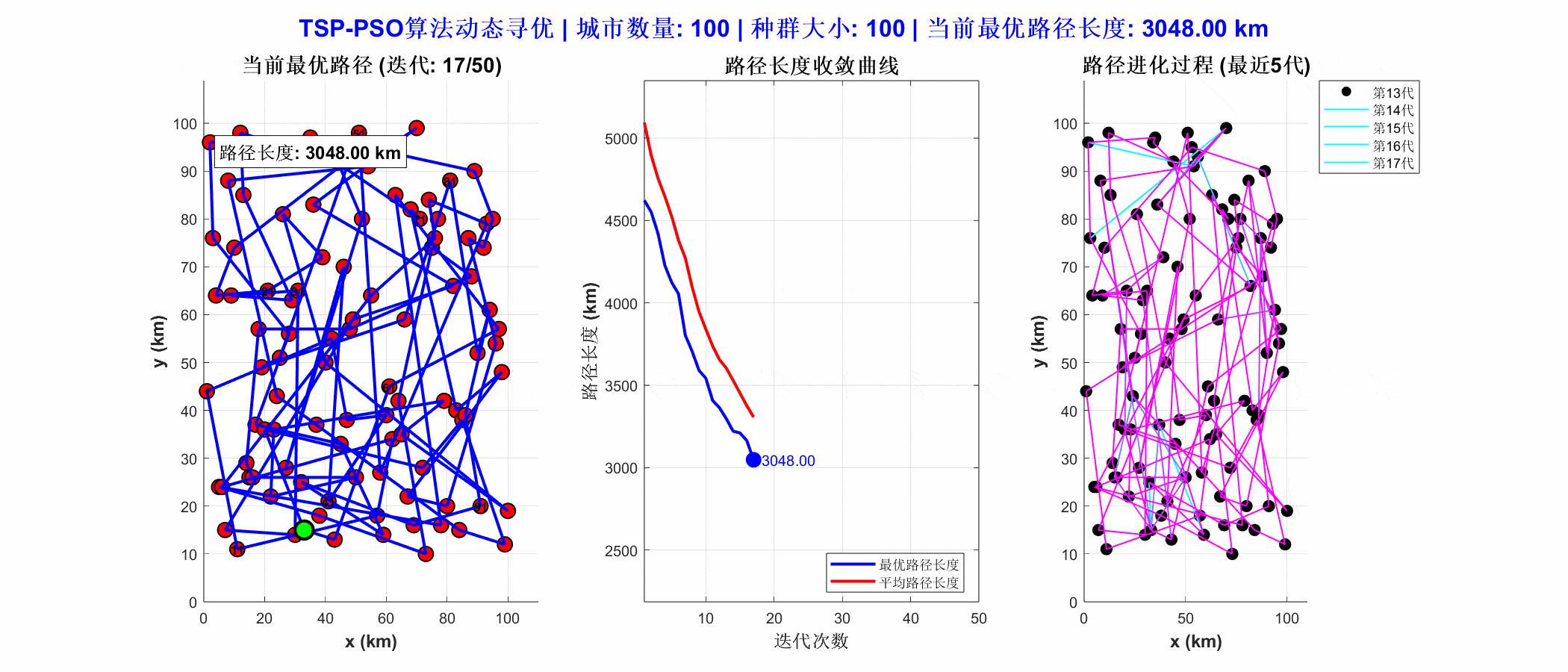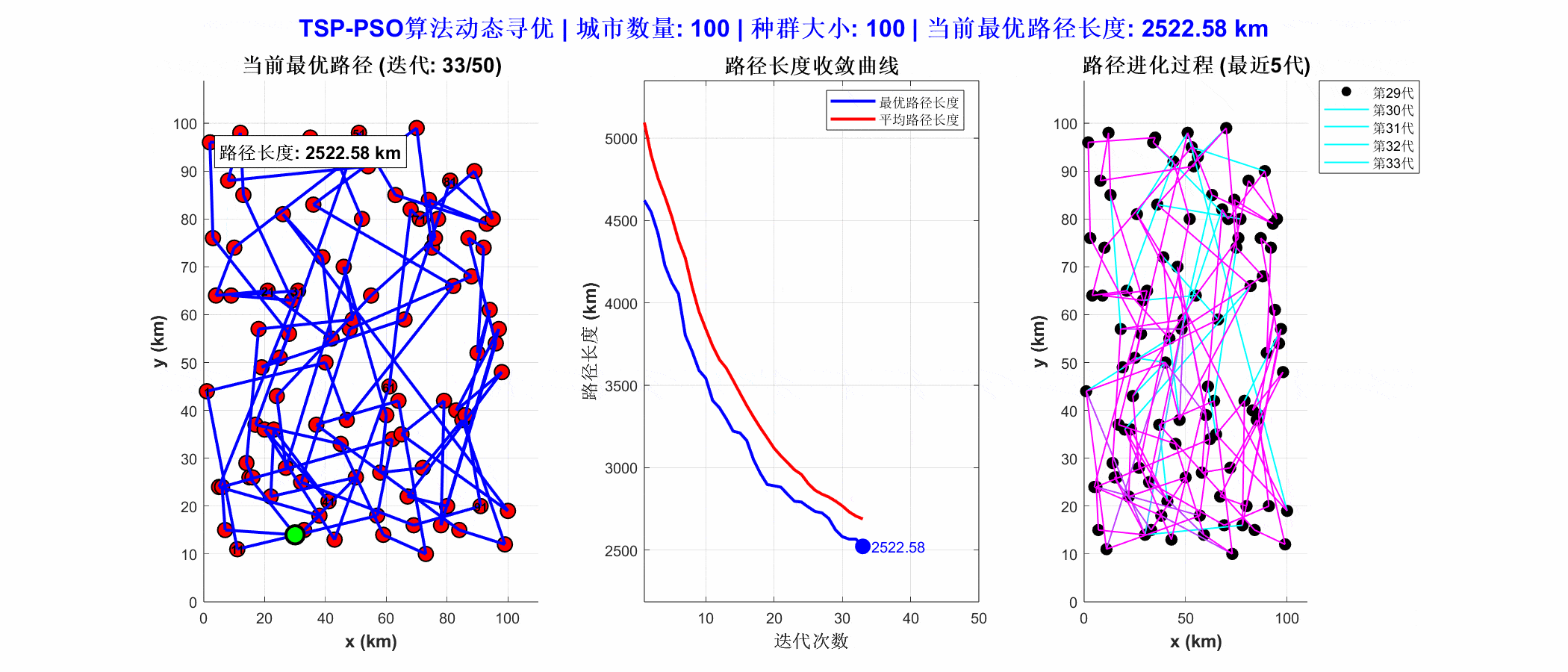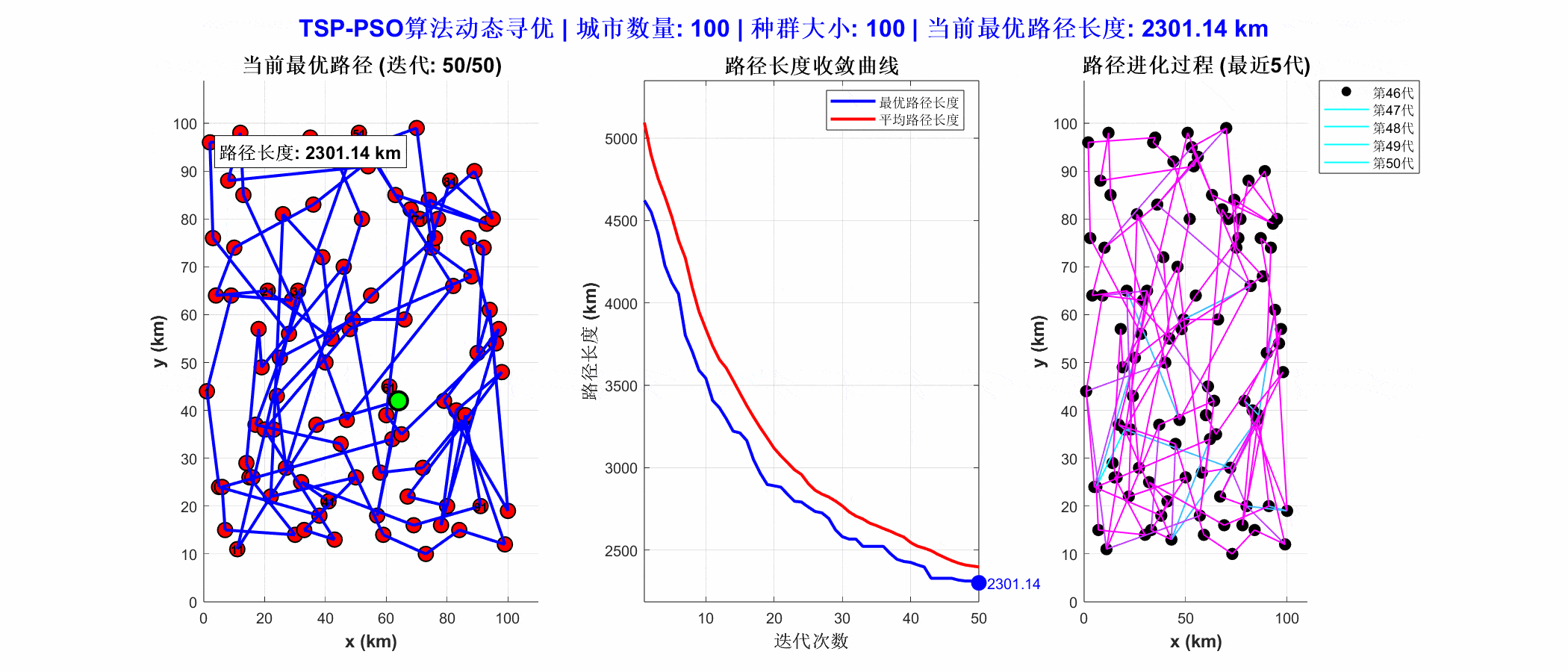
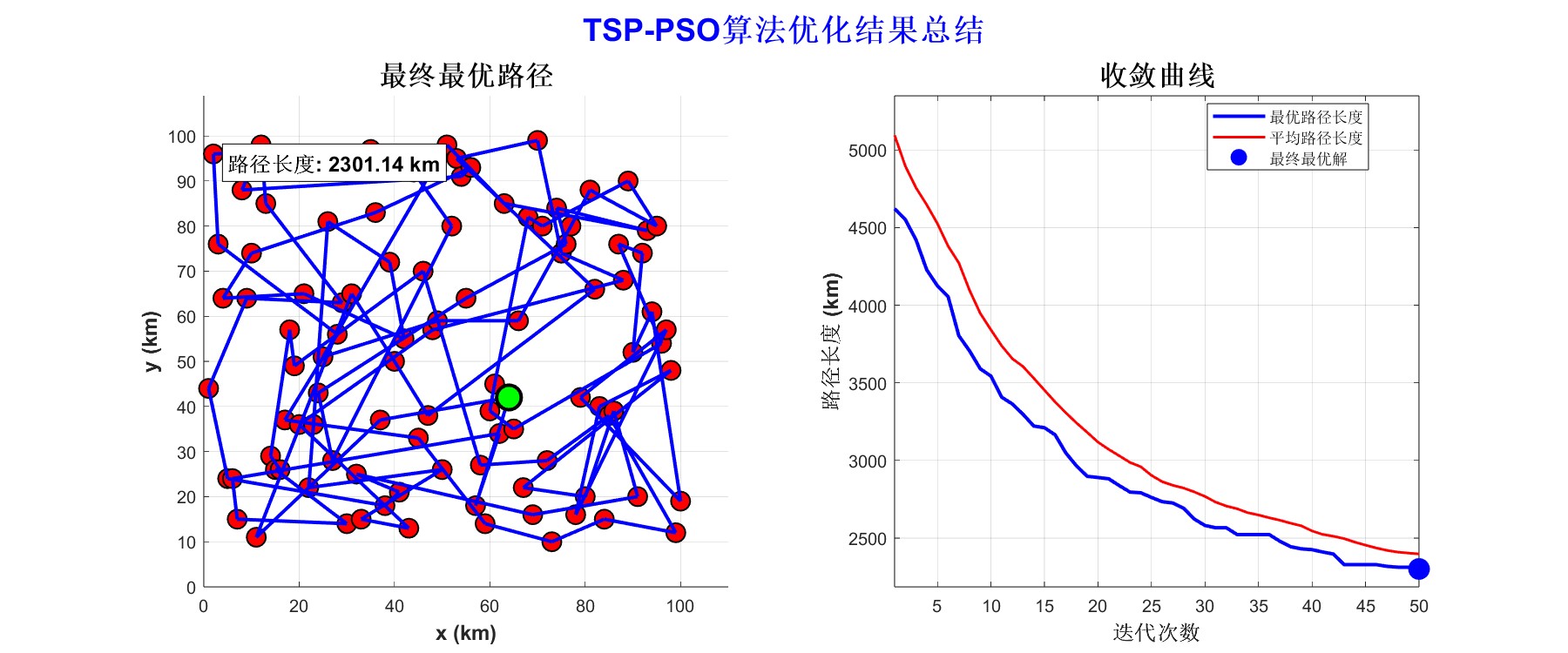
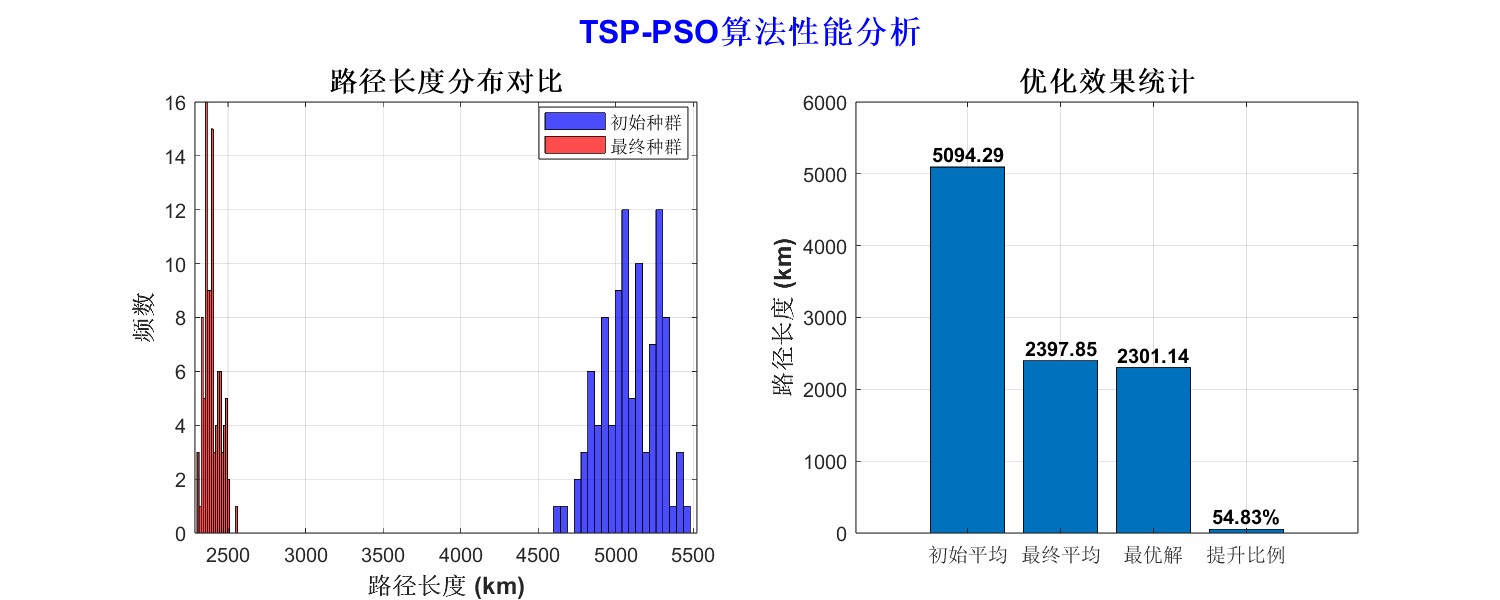

从运行结果可以看出,PSO算法通过离散编码方式表示城市访问顺序,成功找到一条较优的闭合路径。运行结果图中路径清晰,且总距离较短,说明PSO在组合优化问题中具有较强的搜索能力。结合局部搜索策略(如2-opt)后,PSO算法能进一步提升路径质量,适用于物流配送、巡检路线规划等实际问题。
多智能体路径规划
经典 MAPF 问题:经典 MAPF(Multi - Agent Path Finding,多智能体路径搜索)问题是多智能体路径规划领域的基础核心问题,核心是为多个智能体在共享环境中规划无碰撞路径,使其从各自起点抵达对应终点。该问题常见于自动化仓储机器人调度、无人机编队飞行等场景的简化模型,是研究多智能体协同避碰、路径协调的基础。
1、问题描述
双小鼠寻奶酪
在一个简单的4×4栅格环境中:
- 小鼠1:起点S₁(1,1),目标G₁(4,4)
- 小鼠2:起点S₂(1,4),目标G₂(4,1)
- 冲突点:单元格C(2,2)是两条路径的潜在冲突点
- 目标:为两只小鼠规划无碰撞路径,让它们都能安全到达各自的奶酪位置。
2、PSO解题思路
- 粒子表示:每个粒子表示一个完整的路径方案,即两只小鼠的路径序列组合。位置编码为离散的网格坐标序列,速度表示为位置调整的概率向量。
- 适应度函数:路径总长度与碰撞惩罚的加权和(如 fitness = 总路径长度 + 100×碰撞次数 + 50×目标未达惩罚),以最小化适应度值为目标。
- 初始化:随机生成多个合法路径作为粒子初始位置,确保路径从起点开始、在网格范围内移动、避免障碍物。速度初始化为零或小随机调整概率。
- 更新策略:
- 速度更新:在离散PSO中,速度定义为路径调整的倾向性,包括:惯性部分:保持当前路径特征;认知部分:向个体历史最优路径学习;社会部分:向群体最优路径方案学习;
- 位置更新:根据速度应用路径调整操作,生成新路径方案:路径片段替换:用最优路径的片段替换当前路径;等待步插入:在冲突点前插入等待步数避免碰撞;局部优化:调整路径段以缩短距离或避开冲突。
- 终止条件:当最优路径方案不再改善或达到最大迭代次数时停止。
- 关键点:PSO需结合冲突避免策略(如时间差规划)提升解质量,并确保路径满足多智能体约束(无碰撞、各自到达目标)。
3、简单代码
 4、结果展示
4、结果展示
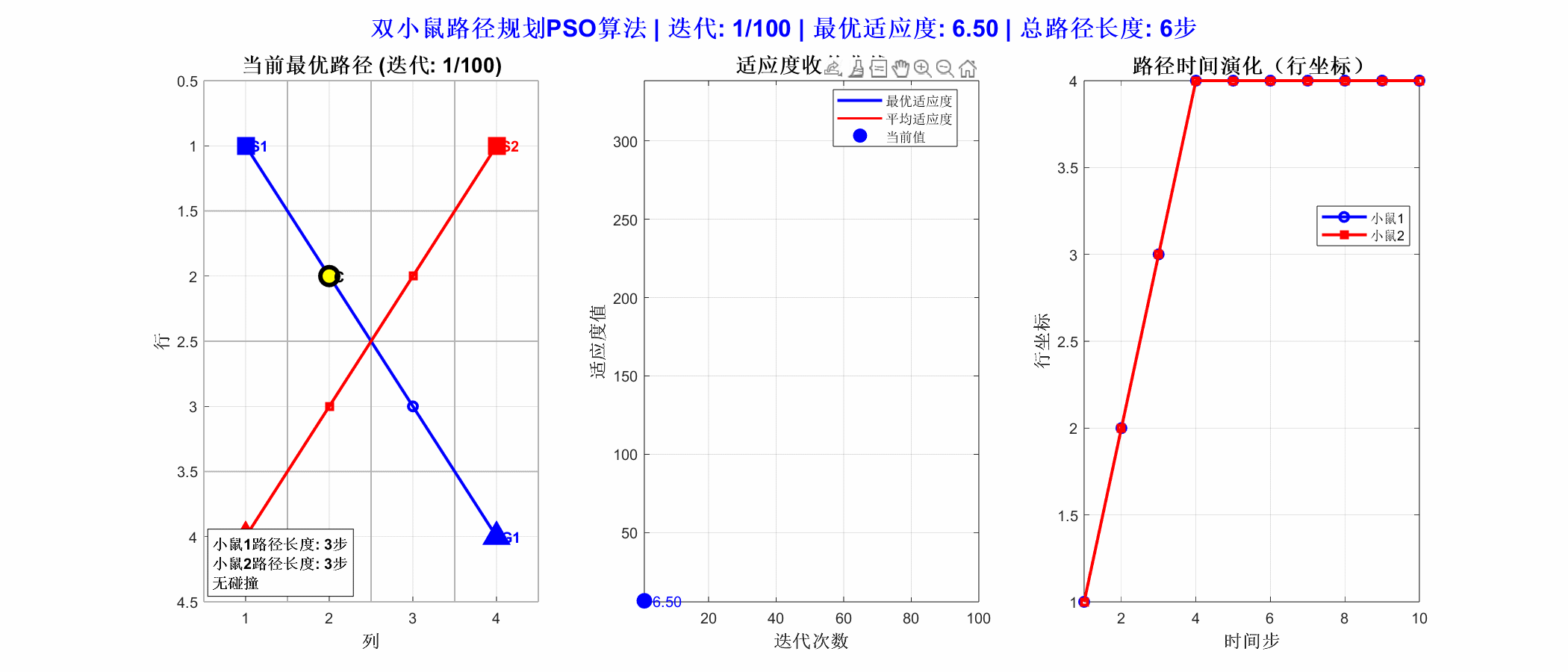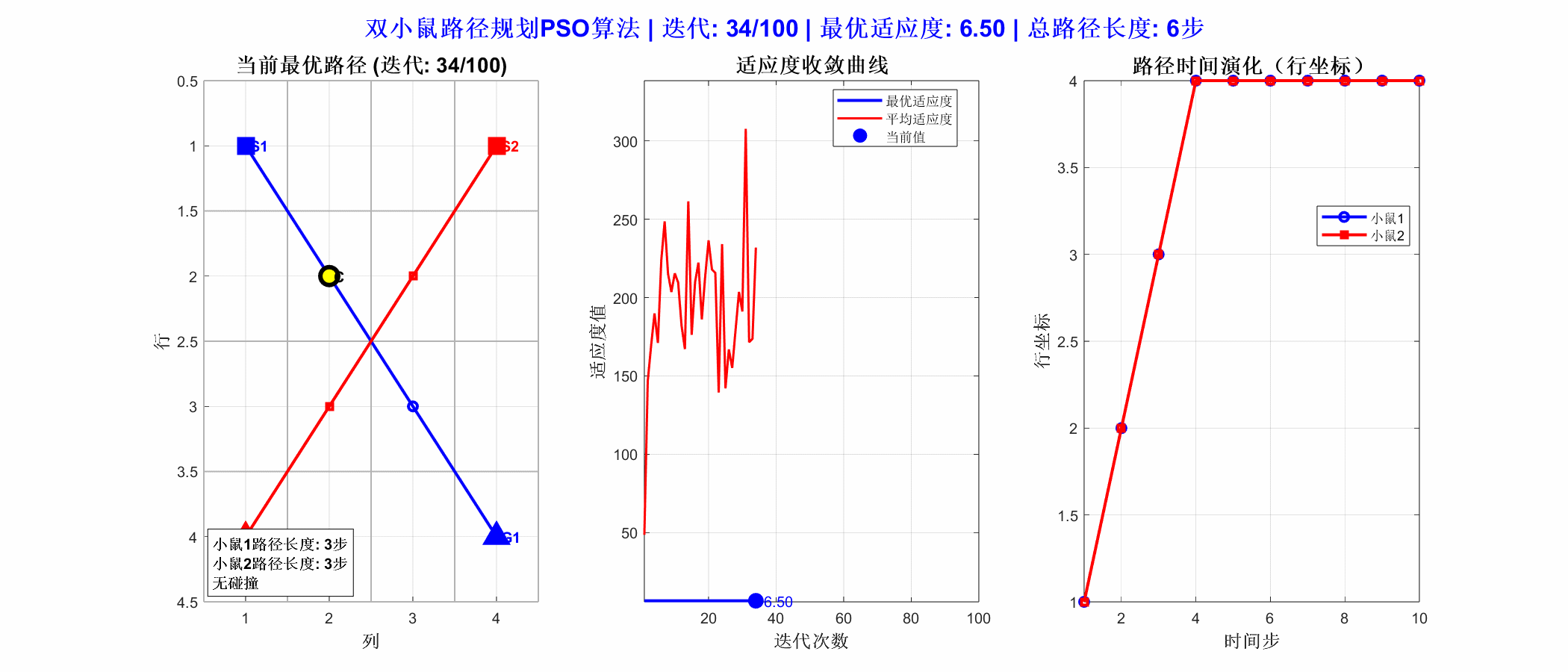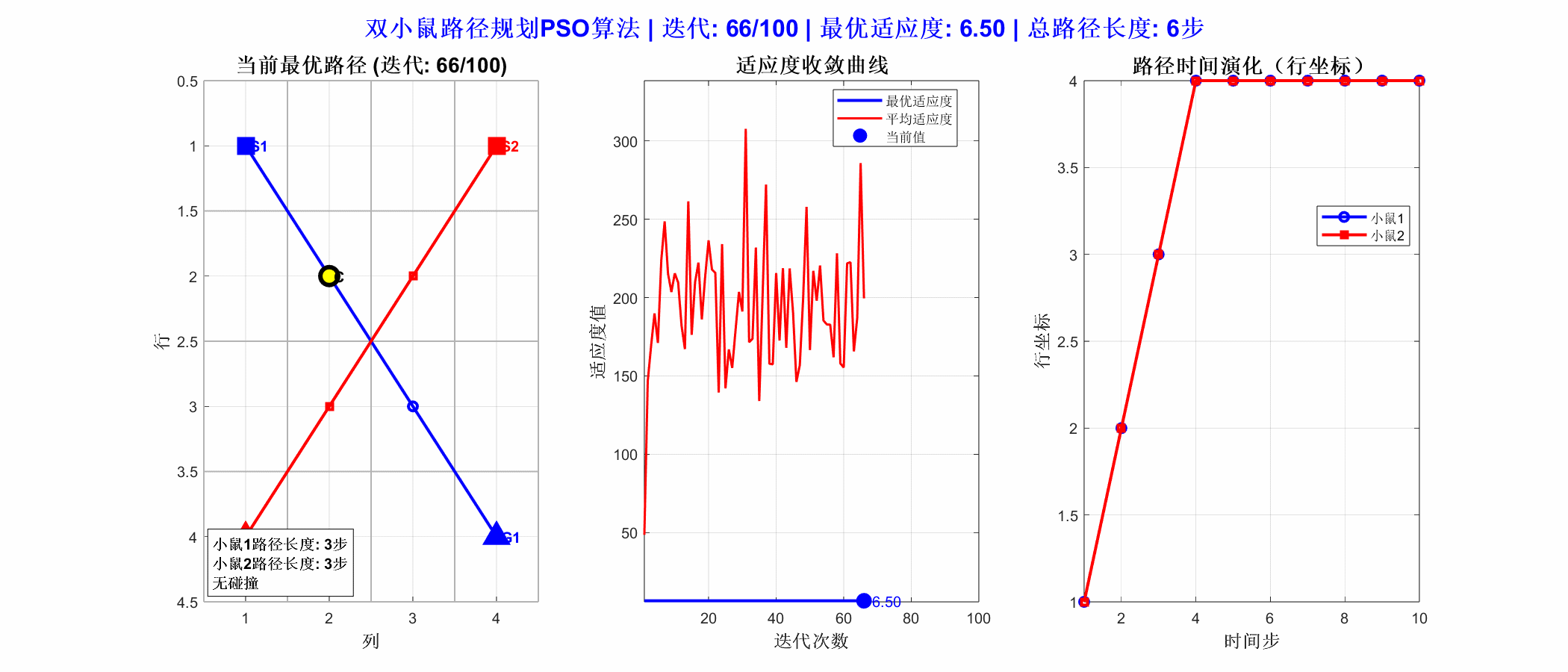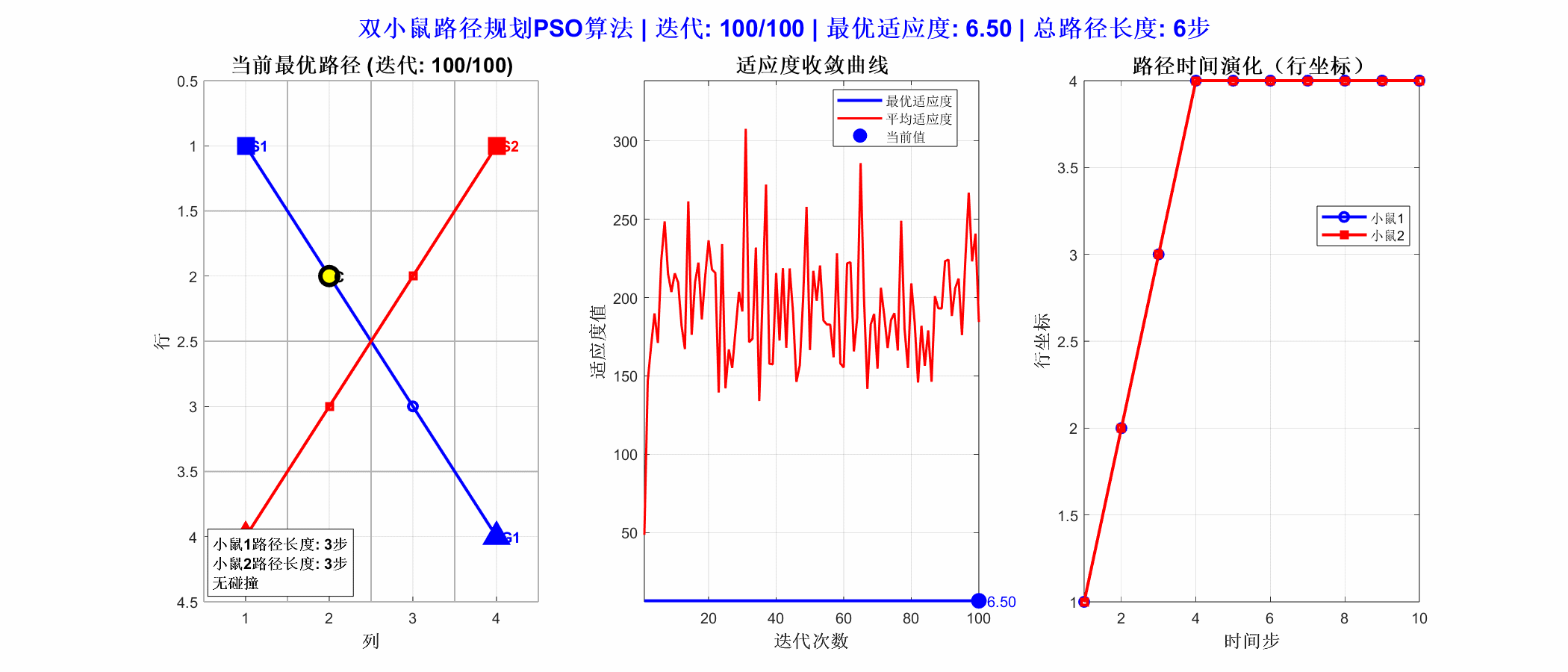
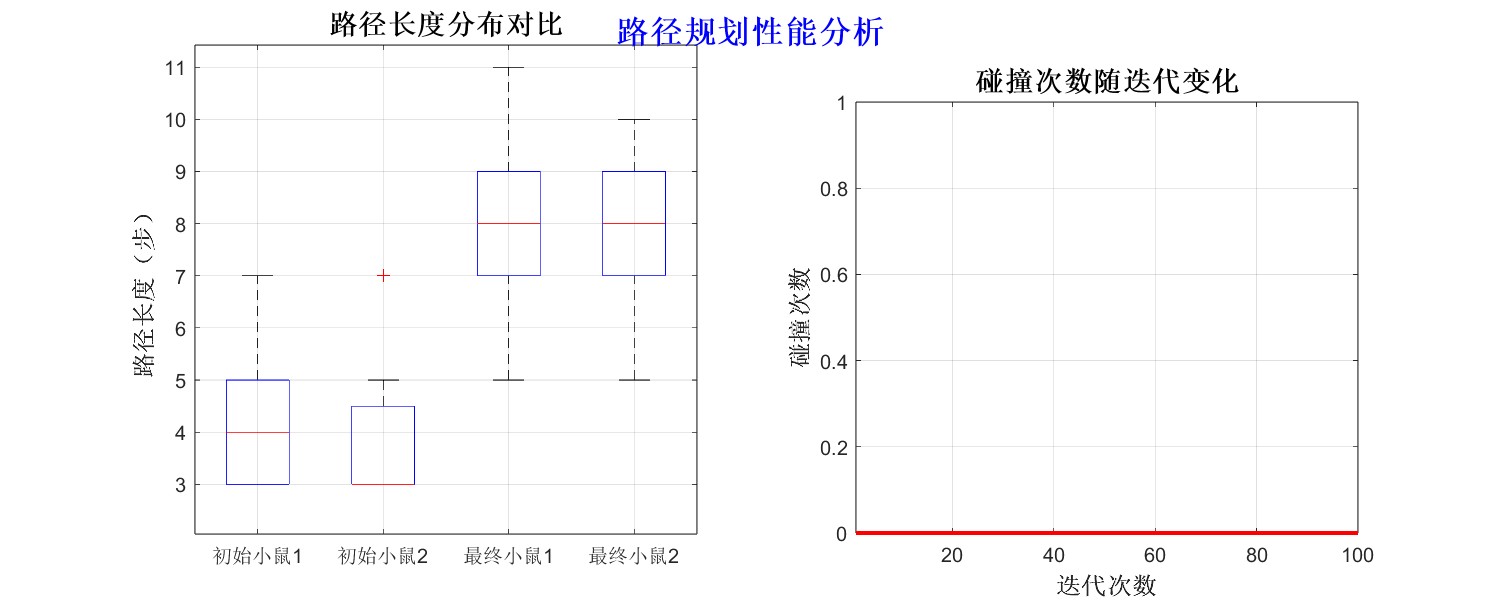
从运行结果可以看出,PSO算法为两个智能体规划出了无碰撞路径。图中两条路径在冲突点处通过时间或空间错开,成功避免了碰撞。这表明PSO能有效处理多智能体协同与避障约束,适用于仓储机器人调度、无人机编队等需要协同路径规划的场景。其适应度函数中融入碰撞惩罚机制,进一步强化了路径的安全性与可行性。
总结
从鸟群的集体智慧到代码的精准优化,粒子群算法以其简洁的架构和出色的性能,已经成为优化工具箱中不可或缺的利器。无论是函数优化还是路径规划,PSO都能以最少的计算成本找到满意的解。粒子群算法向我们展示了自然启发的计算之美。它提醒我们:有时候,最复杂的问題往往有最简单的解决方案。下次当你面对优化挑战时,不妨让这些"智能粒子"为你指引方向。
作者 | 马瑞 元晨晨
责编 | 邱宇
审核 | 徐小峰