目录
刷题记录专题正式开启啦，每篇博客会分享3道leetcode热题，会附上原题连接，以及个人对本题的理解和个人解题给小伙伴提供解题的思路，算法题无论是对提升自己还是后续秋招、春招面试，都是很重要的，这个专题后续也会持续更新，话不多说，让我们一起开启刷题记录日志1吧~
矩阵篇热题一
原题网址
48. 旋转图像 - 力扣（LeetCode）
https://leetcode.cn/problems/rotate-image/description/
题目描述
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
要求：你必须在**原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
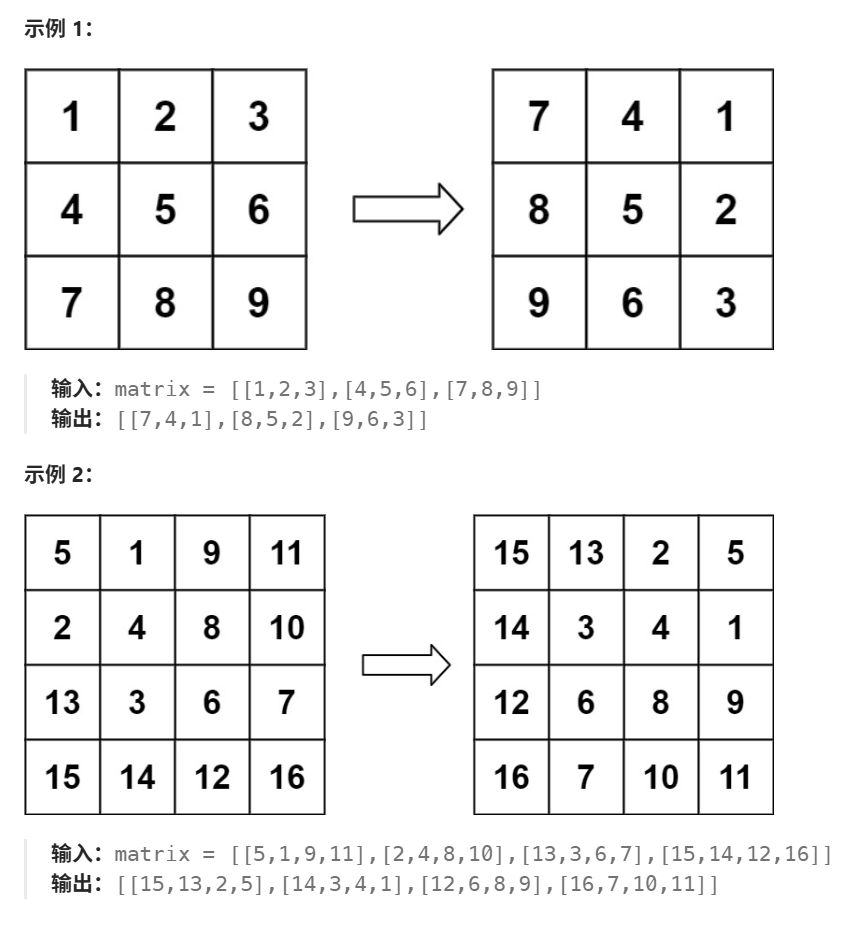
思路解析
题目需要将矩阵中的数据按顺时针方向旋转90°，这里先将矩阵沿着正对角线交换正对角线上、下区域的数据
如上图将上下区域的数据进行交换后，原矩阵外圈中顶部这一行的数据原本顺时针移动后应该去到外圈的右边这一列，原矩阵外圈左边这一列顺时针旋转后应该去到顶部这一行。但是当我们沿对角线交换数据后，原矩阵外圈顶部数据，被移动到了左边这一列，原矩阵左边这一列被移动到了外圈顶部。（原矩阵右边这一列和底部这一行沿正对角线交换后的问题原理同上）现在解决本道题转化为下面两个问题
问题1：原矩阵左边这一列虽然被移动到了外圈顶部，但是顺序反了，现在的顺序是5，2，13，15，我们期望的数据是15，13，2，5。
问题2：原矩阵顶部一行被移动到了左边这一列，但是理应被移动到右边这一列。
通过问题1和2，我们发现倘若现在沿中间将矩阵分为左右两侧，后交换交换左右两侧的数据，便可得到目标矩阵。
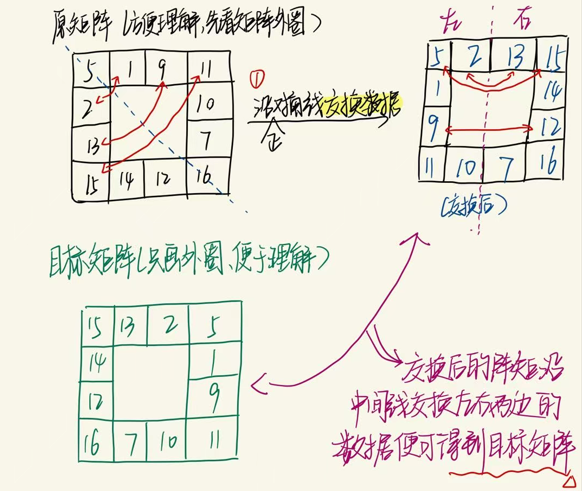
交换矩阵左右两侧的数据
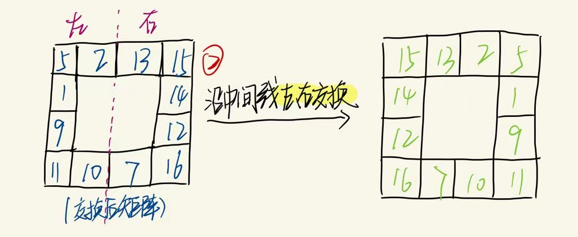
交换完数据后，可以发现目前矩阵的数据与目标矩阵数据相一致。上面为了方便大家的理解只拿矩阵的外圈进行了演示。将矩阵拆成一圈一圈，由外向内，层层递进，可以发现每一圈解题的思路都是一样的。对整个矩阵的操作就如同上述对单圈的操作。由此即可得到本题的题解如下：
解题步骤：
①沿正对角线交换正对角线上下区域的区域；
②在①的基础上，沿正中间交换左右两边的数据
完整的解题思路
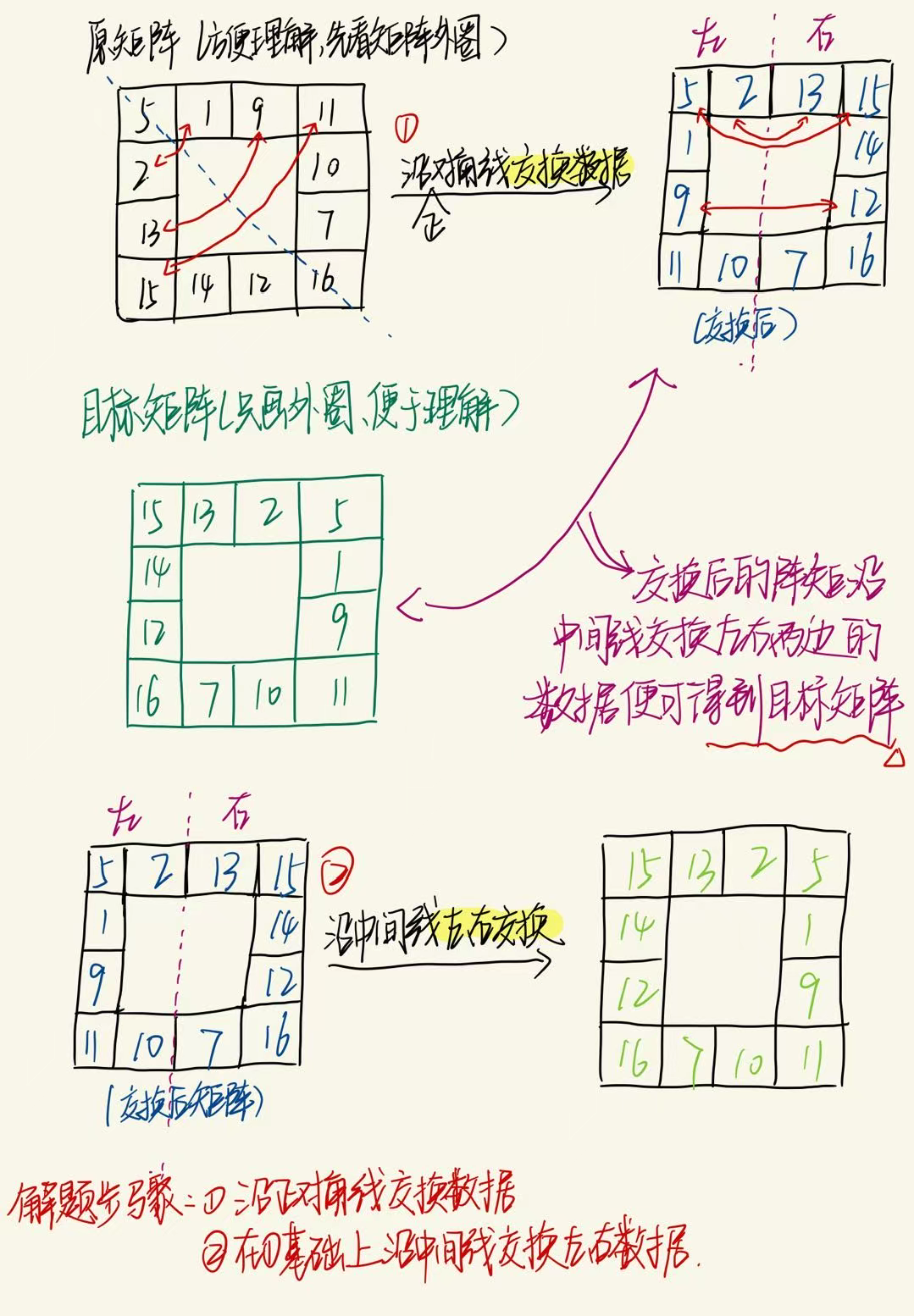
个人题解
java
class Solution {
public void rotate(int[][] matrix) {
//交换正对角线的数据
int len_row=matrix.length;//行数
int len_col=matrix[0].length;//列数
for(int i=0;i<len_row;i++){
for(int j=i+1;j<len_col;j++){
//交换正对角线对应元素
int cur=matrix[j][i];
matrix[j][i]=matrix[i][j];
matrix[i][j]=cur;
}
}
//交换左右的元素
for(int i=0;i<len_row;i++){
int left=0;
int right=len_col-1;
while(left<right){
int cur=matrix[i][left];
matrix[i][left++]=matrix[i][right];
matrix[i][right--]=cur;
}
}
}
}矩阵篇热题二
原题网址
54. 螺旋矩阵 - 力扣（LeetCode）https://leetcode.cn/problems/spiral-matrix/description/
题目描述
给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。
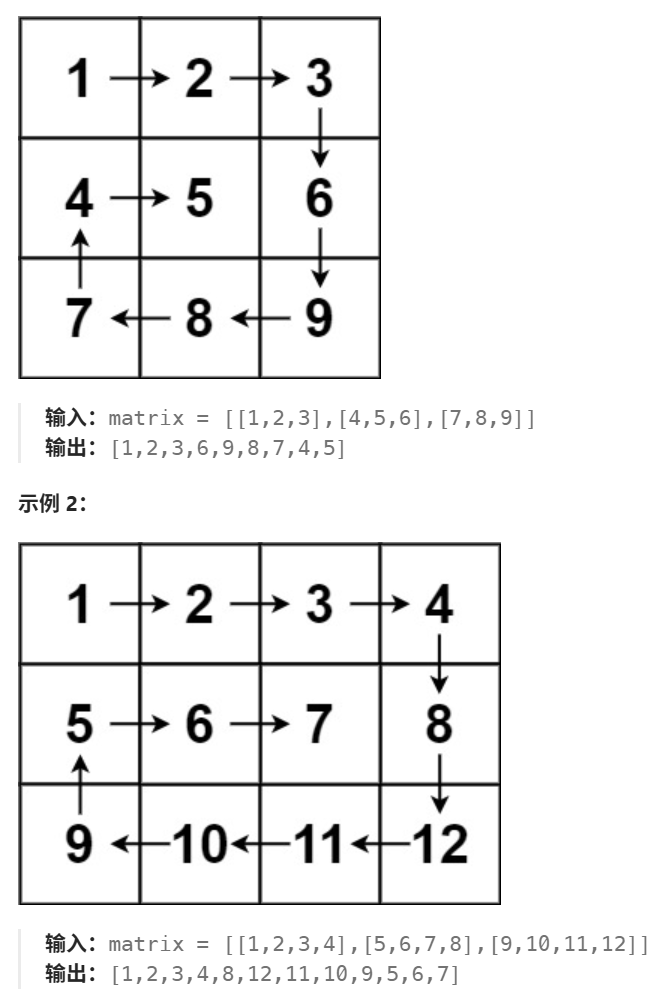
思路解析
和上题一样，我们将矩阵拆分为一圈一圈（便于理解）
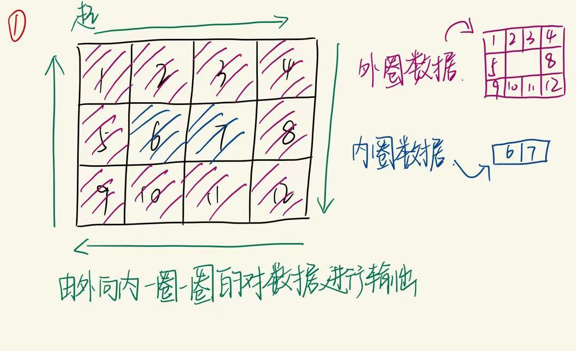
现在我们得到外圈数据和内圈数据，依据题目输出螺旋而言，就是先按顺时针顺序输出外圈数据，然后把圈缩小，缩小后得到的新圈（上图内圈），再一次按照之前输出外圈的步骤输出内圈数据。直到最终输出所有数据。
现在大致思路有了，在进一步思考，每次应该怎么确定输出数据的范围呢？也就是圈的固定，这里需要用到四个变量，left、top、right、bottom
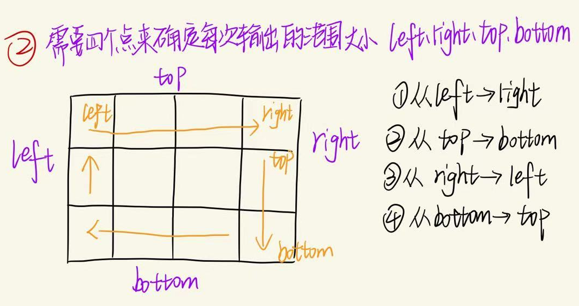
left:确定圈的左侧，固定左侧纵坐标（最小纵坐标），取值 left=0
top:确定圈的上侧，固定顶部横坐标（最小横坐标），取值 top=0
right:确定圈的右侧，固定右侧纵坐标（最大纵坐标），取值 right=matrix[0].length-1
bottom:确定圈的底侧，固定底部横坐标（最大横坐标），取值 bottom=matrix[0].length-1
举个例子：按照顺时针，①首先需要获取第一行的数据，循环的输写应该是
java
for(int i=left;i<=right;i++){
// matrix[top][i] ->获取首行这一列数据，横坐标固定，刚好为 top 所记录的值
}第一行数据成功获取到后，②现在需要获取圈右侧这一列的数据，注意这里在获取第一列数据之前需要 top++，因为已经获取到了第一行的所有数据，也就包括了外圈右侧这一列的第一个数据，现在需要从上往下进行数据的获取，循环的书写应该是
java
//伪代码
top++;
if(top>bottom) break; //稍后解释
for(int i=top;i<=bottom;i++){
// matrix[i][right]; -> 获取圈右侧这一列数据，纵坐标固定，刚好为 right 所记录的值
}第③步就是获取底部从右到左的数据，原理和上面从左到右一样，但是这里需要注意的一个点是，在写循环之前需要right-- ，因为之前获取右侧这一列时，已经获取到了最底下这一行从右到左的最右的这一个数据。循环的书写为
java
right--;
if(left>right) break;
for(int i=right;i>=left;i--){
// matrix[bottom][i] ->获取圈底部这一行数据，横坐标固定，刚好为 bottom 所记录的值
}第④步就是获取最左侧且从下到上的数据，原理和上面第②步从上到下是一样的，同样需要注意的点是，在循环书写前我们需要将 bottom-- ，因为我们已经获取到最左侧这一列最底部的数据，还有一个值得注意的点是，最左侧且从下到上的数据中最顶部的那个数据我们在获取第一行的时候就已经获取了，所以说我们第④步获取的数据其实需要除去最底部和顶部的两个数据，这里除去最底部我们将bottom-- 了，最顶部呢？？别忘记了，在执行第②步之前我们已经将 top++ 了，现在 top 刚好指定的首部在第二行，满足我们的需求，循环的书写应该是
java
bottom--;
if(top>bottom) break;
for(int i=bottom;i>=top;i--){
// matrix[i][left] ->获取圈左侧这一列数据，纵坐标固定，刚好为 left 所记录的值
}
left++;//最外圈左侧获取完毕，开始固定次外圈的最小纵坐标
if(left>right) break;在走完第④步之后，需要将 ***left++ 。***最外圈的左侧一列数据已经获取完毕了，现在需要将圈缩小，左侧代表最小纵坐标的值应当+1。
在第②步代码片段时，写道 if(top>bottom) break; 这里break跳出的循环又是什么呢？？在本题我们是将二维矩阵看成一圈一圈，每一圈的操作步骤都一样，依次获取首行、右列、底行、左列的数据，因此我们可以使用一个大的 while 循环包裹这四个小的 for 循环。显然循环的条件为 ***top>=bottom && left<=right ，***因为每走完一圈，top++、bottom--、left++、right--，top与bottom，left与right在无限的接近。当 top>bottom，left>right 时说明所有的矩阵可拆成的圈已经被遍历完毕。
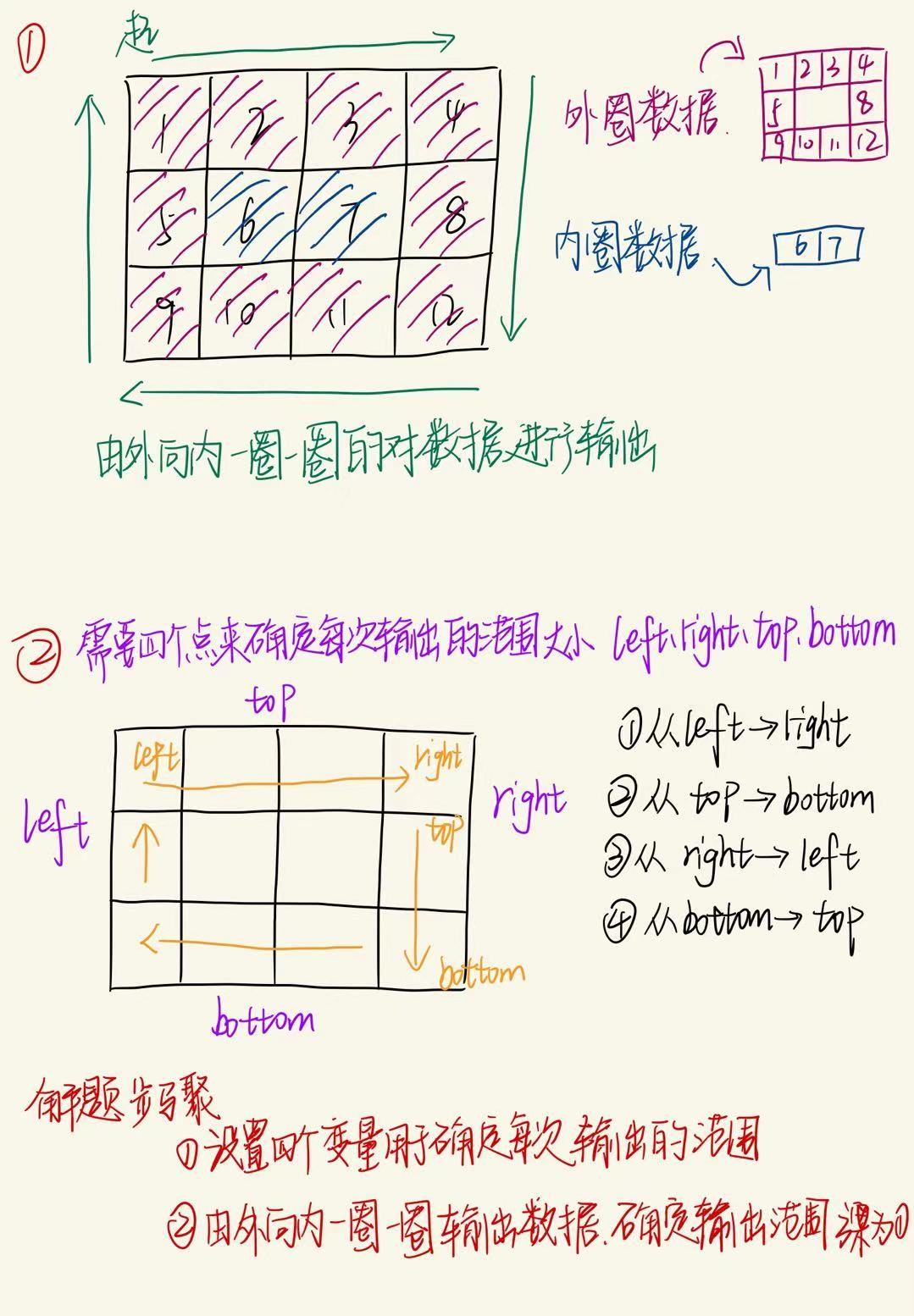
个人题解
java
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> result=new ArrayList<>();
int left=0,right=matrix[0].length-1,top=0,bottom=matrix.length-1;
while(left<=right && top<=bottom){
for(int i=left;i<=right;i++){
result.add(matrix[top][i]);
}
top++; if(top>bottom) break;
for(int i=top;i<=bottom;i++){
result.add(matrix[i][right]);
}
right--; if(right<left) break;
for(int i=right;i>=left;i--){
result.add(matrix[bottom][i]);
}
bottom--; if(bottom<top) break;
for(int i=bottom;i>=top;i--){
result.add(matrix[i][left]);
}
left++; if(left>right) break;
}
return result;
}矩阵篇热题三
原题网址
240. 搜索二维矩阵 II - 力扣（LeetCode）https://leetcode.cn/problems/search-a-2d-matrix-ii/
题目描述
编写一个高效的算法来搜索 m xn 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
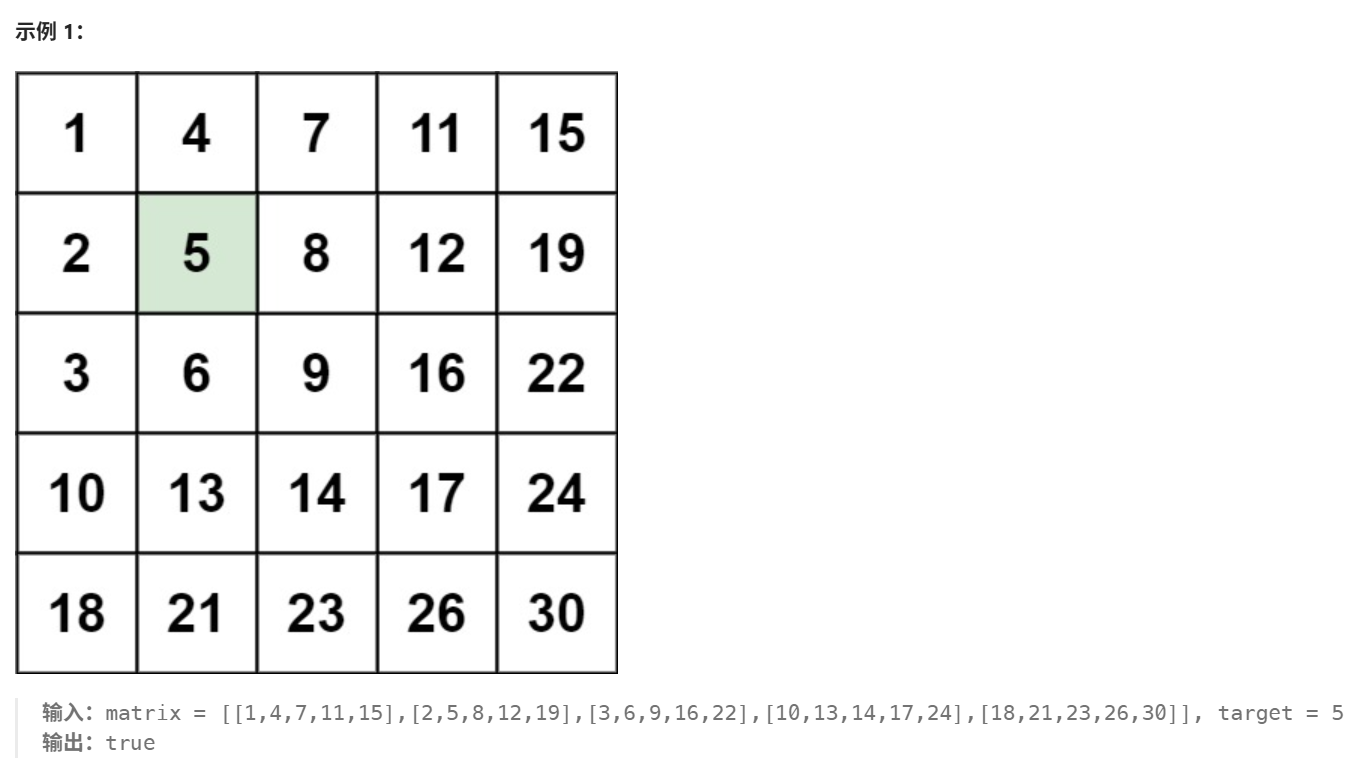
思路解析
看到本题我相信各位小伙伴脑子里肯定已经有了第一个解题方法---遍历整个二维数组。但是题目说编写一个高效的方法来解决本题，这里我们不采取直接遍历整个二维数组的方法。由题目已知这个二位数组的特点，每行从左到右数字增大，每列从上到下数字增大。倘若现在遍历的起始点如下图所示
我们需要判断目标值 target=5 是否出现在二维数组中，现在将 target 与当前起始点数据值15（0，4）进行比较，我们知道15左边的数据值比15小，15下面这一列的数值都比15大，倘若现在目标值大于15，我们可以让15这个数值对应的纵坐标 y++，如果目标值小于15，我们可以让15对应的横坐标 x--。当 x 或 y 发生变动后，会得到一个新的坐标，对新的数据判断方法同上一致，循环往复，若寻找到目标值为 target 的数值，返回true，否则返回false，从时间复杂度分析来看，比直接进行整个二维数组的遍历高效多了。
矩阵1、15、18、30这四个顶点，是否是每个都可以当作起始点呢？？显然不是的，通过观察可以发现1和30不可以，18和15可以。因为1和30两条可以走通的路，对于1来说，两条路都比1大，对于30来说，两条路都比30数值小。当目标值大于1时，不知道是往下走还是往右走。对于30同理，当遇到比30大的数据时，同样不知道是往上走还是往左走。
想要实现上述操作，仍需要通过循环操作，循环的条件为 ***x>=0 || y<=matrix[0].length，***条件
个人题解
java
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
int x = 0, y = n - 1;
while (x < m && y >= 0) {
if (matrix[x][y] == target)
return true;
if (matrix[x][y] > target) {
y--;
} else {
x++;
}
}
return false;
}
}以上就是本期分享的全部内容啦，小伙伴们认为有不对或者可以优化改进的地方还请在评论区进行留言指出，下期内容再见啦~~