CPU与cuda原理,并从其原理来理解flashattention
GPU 和 CUDA结构
cuda的每个block对应gpu中的每个sm(stream multiprocessor ), cuda的一个block可以分为多个warp,一个warp内有32个线程(在不同的数据上执行相同指令)
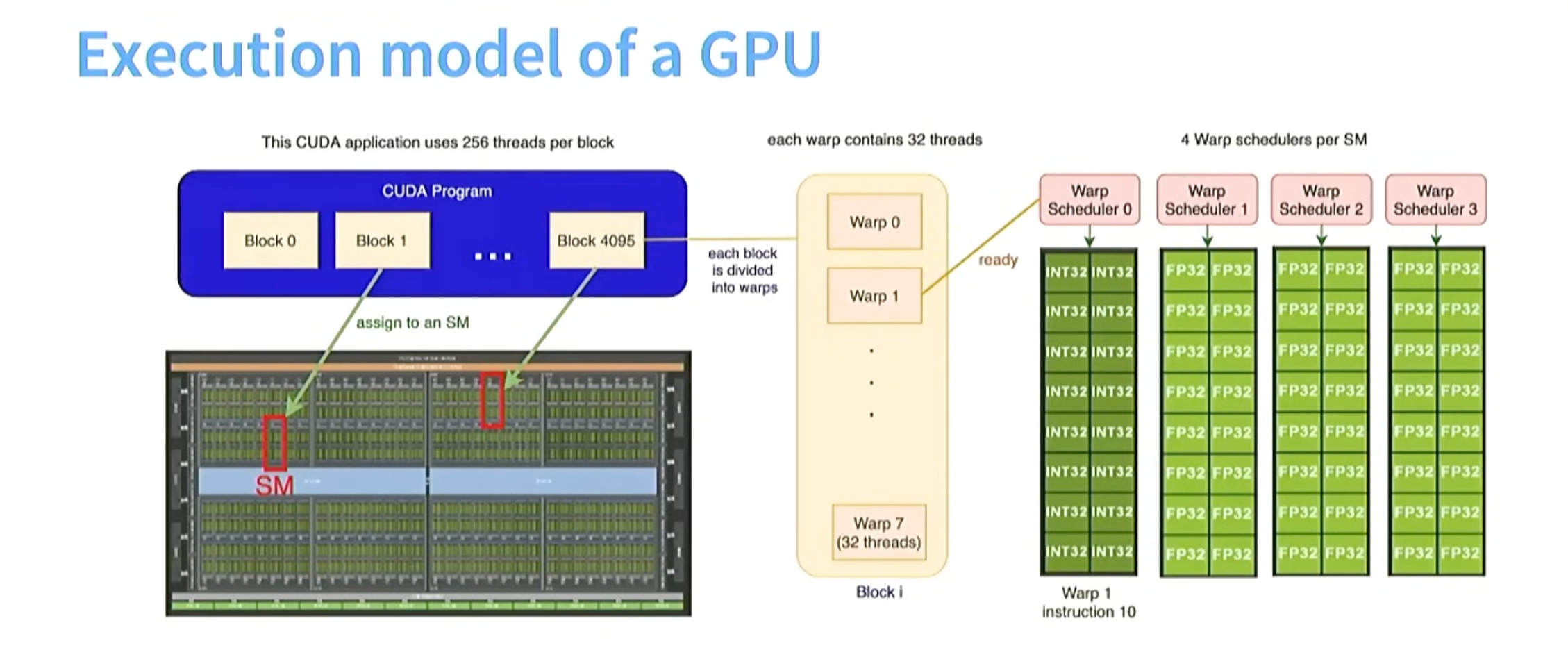
GPU MEMORY结构
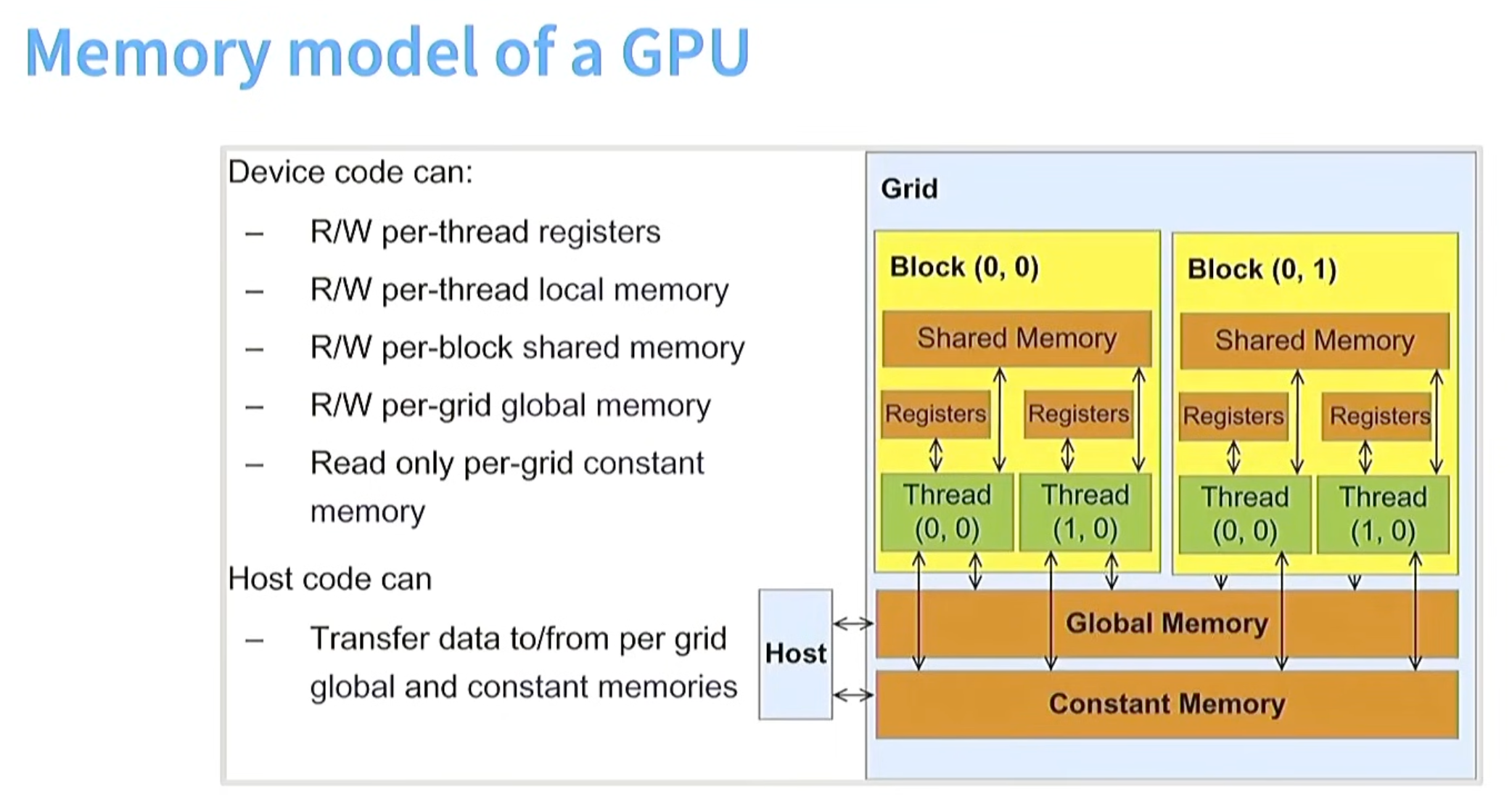
让GPU运行更快的几种方法

技巧0 .条件语句在一个warp中有害,尽量在一个warp中别使用(跟内存无关)
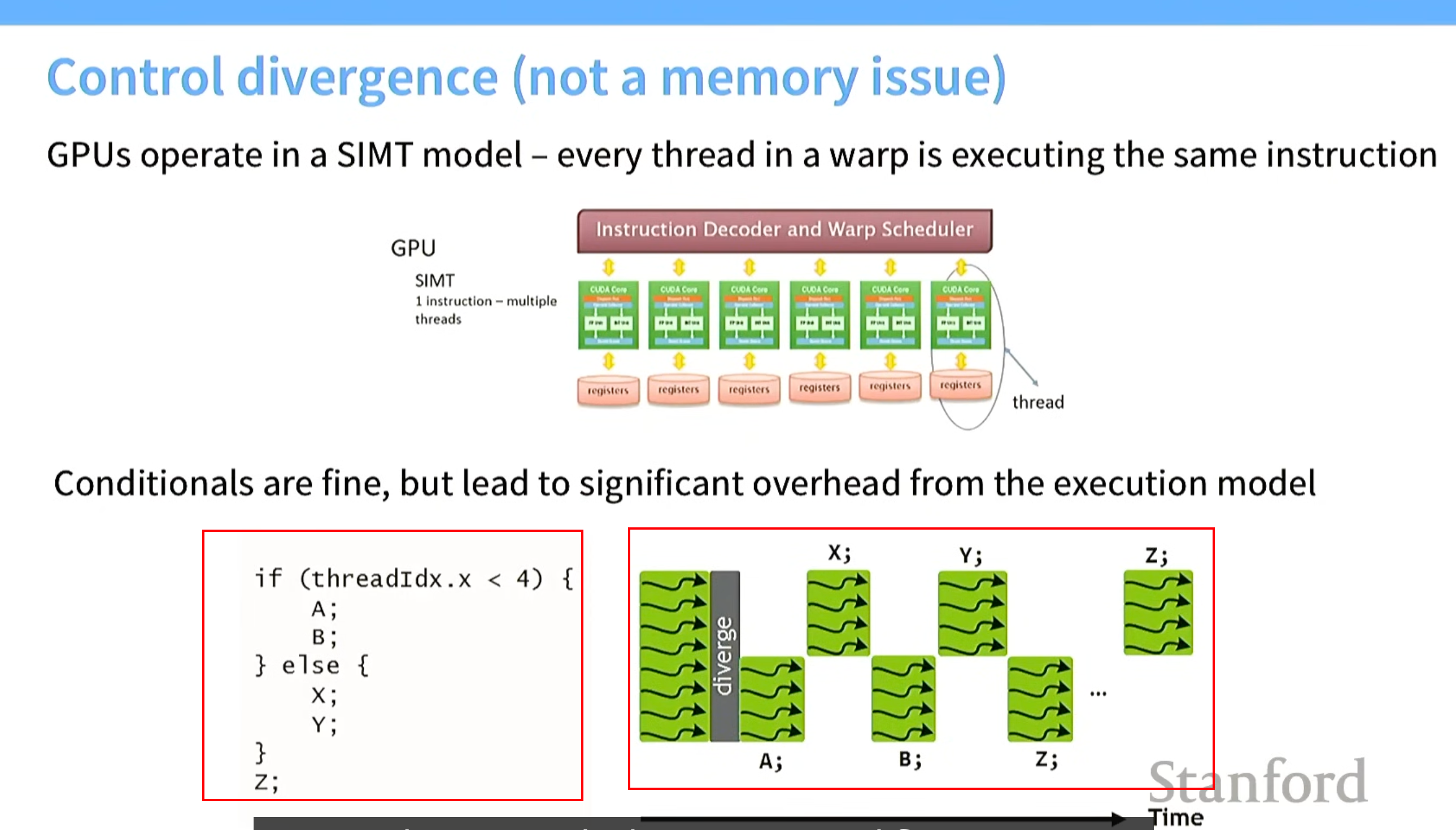
技巧1. 低精度计算(low precision computation)

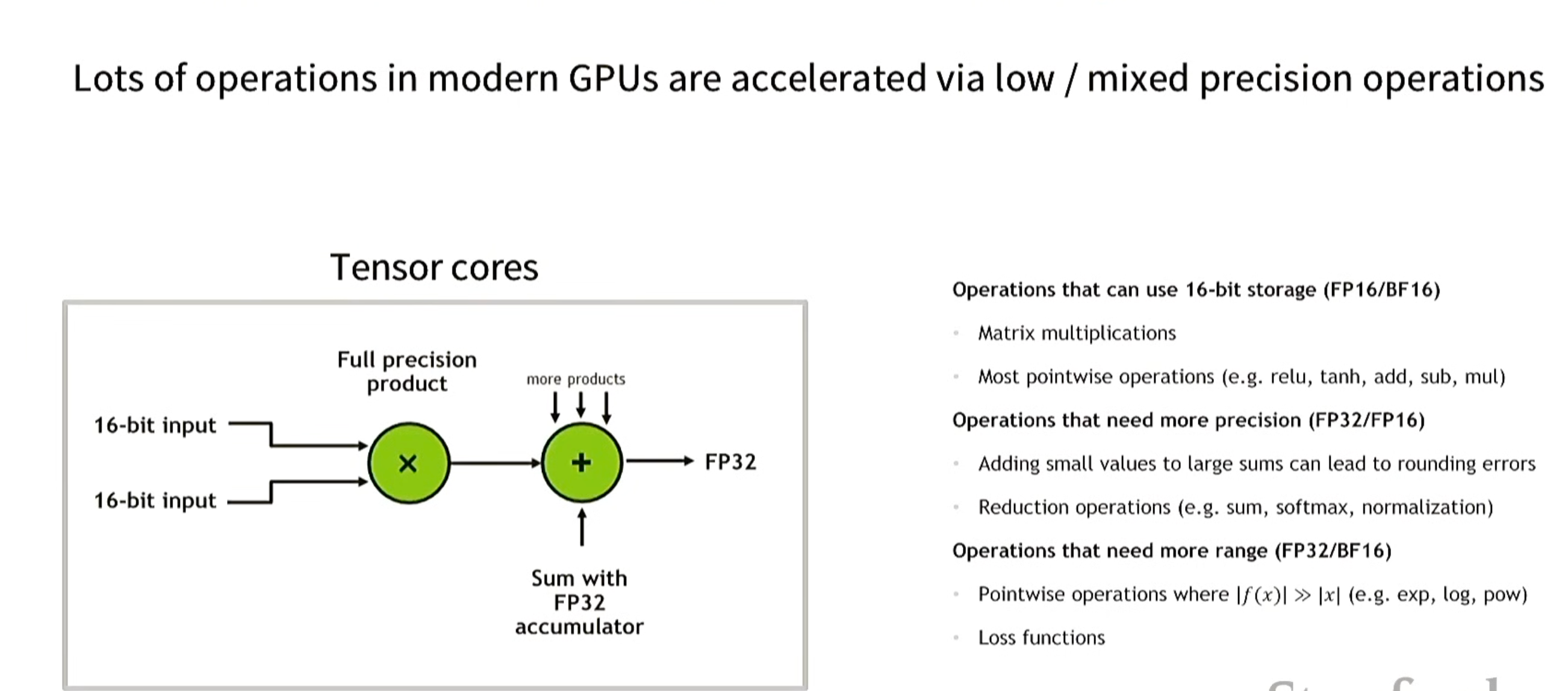
技巧2.内核融合(kernel fused)
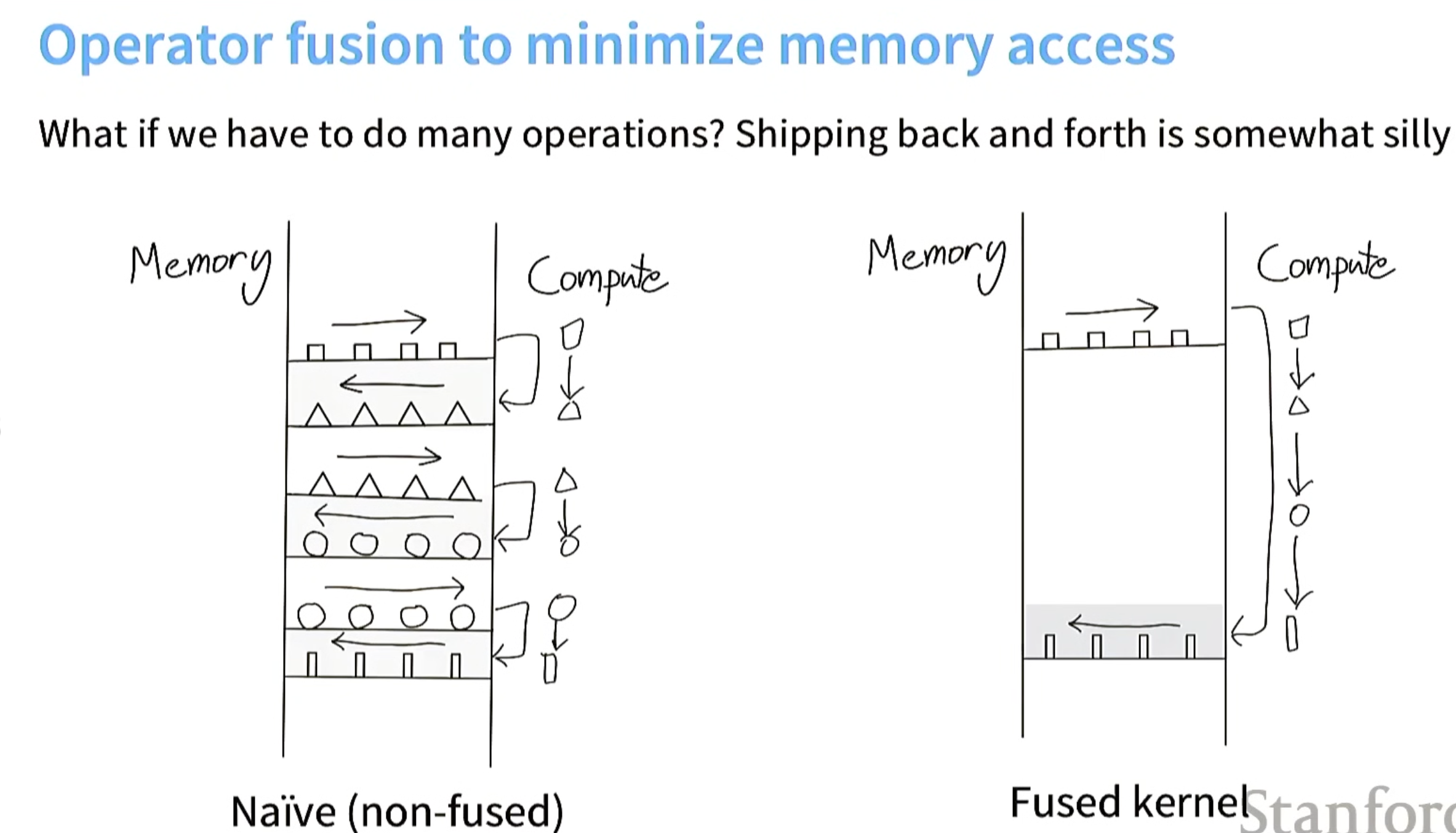
例子 计算 sinx平方 + cosx 平方
没算子融合之前
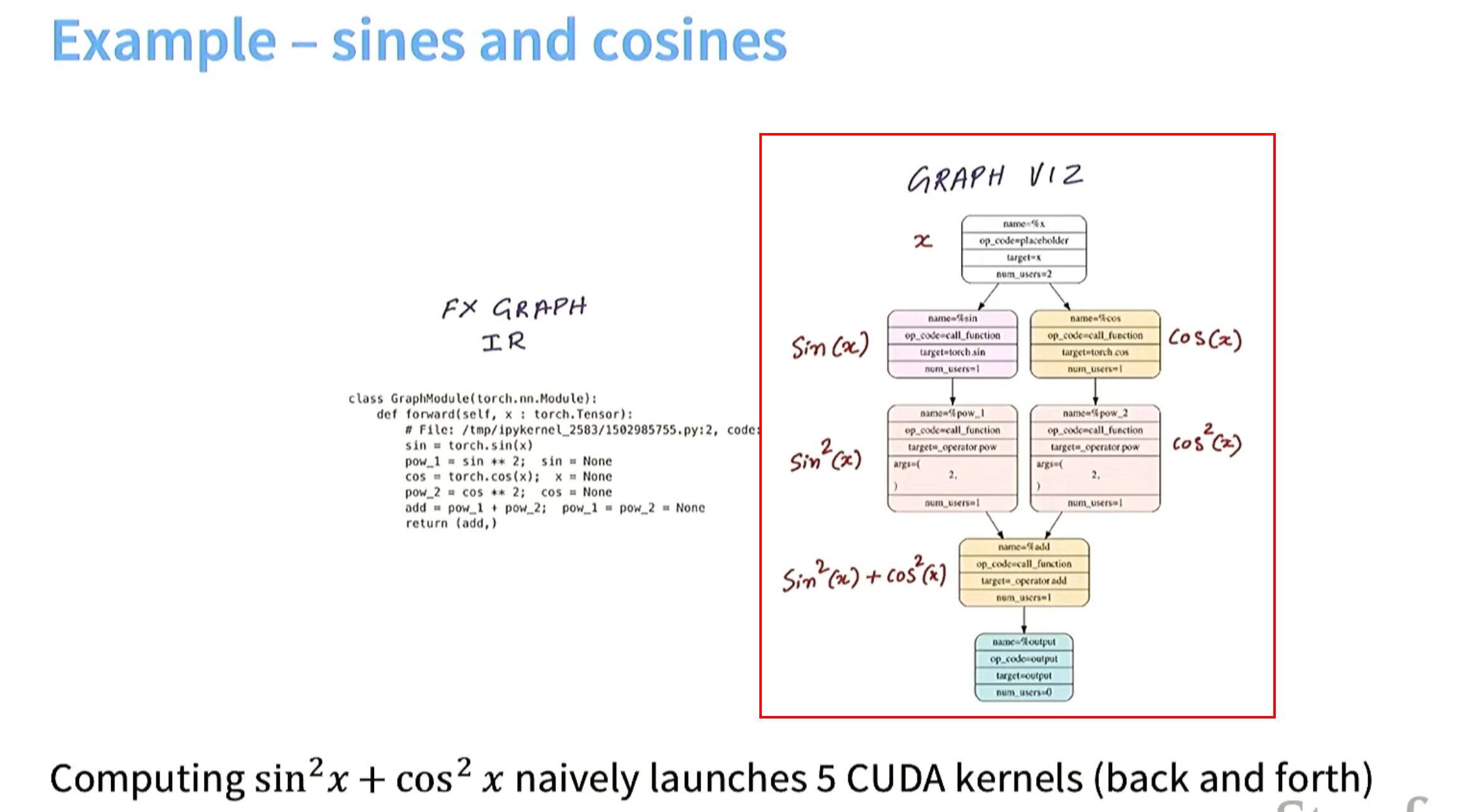
算子融合
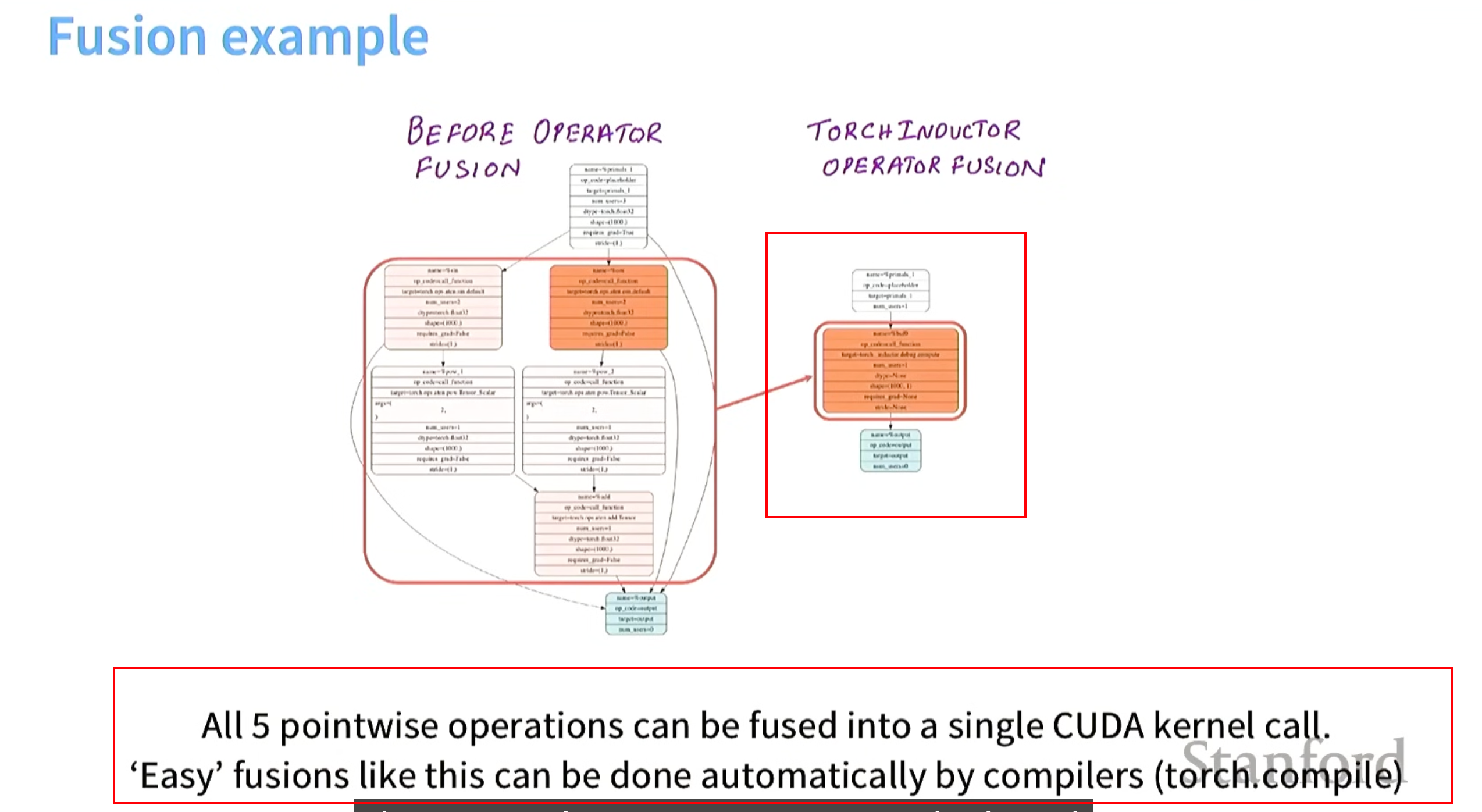
技巧3.重计算(recomputation)(计算换memory)
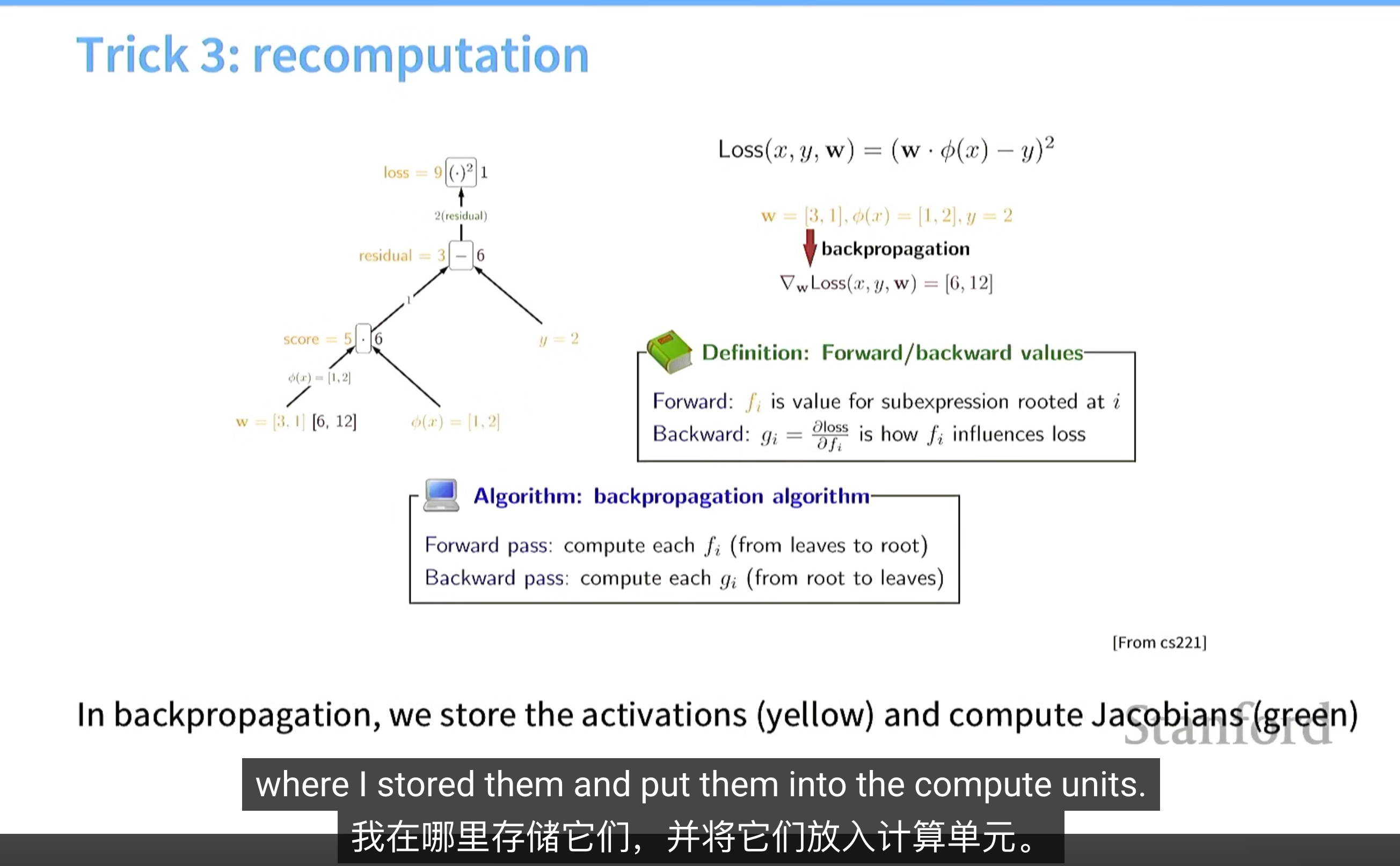
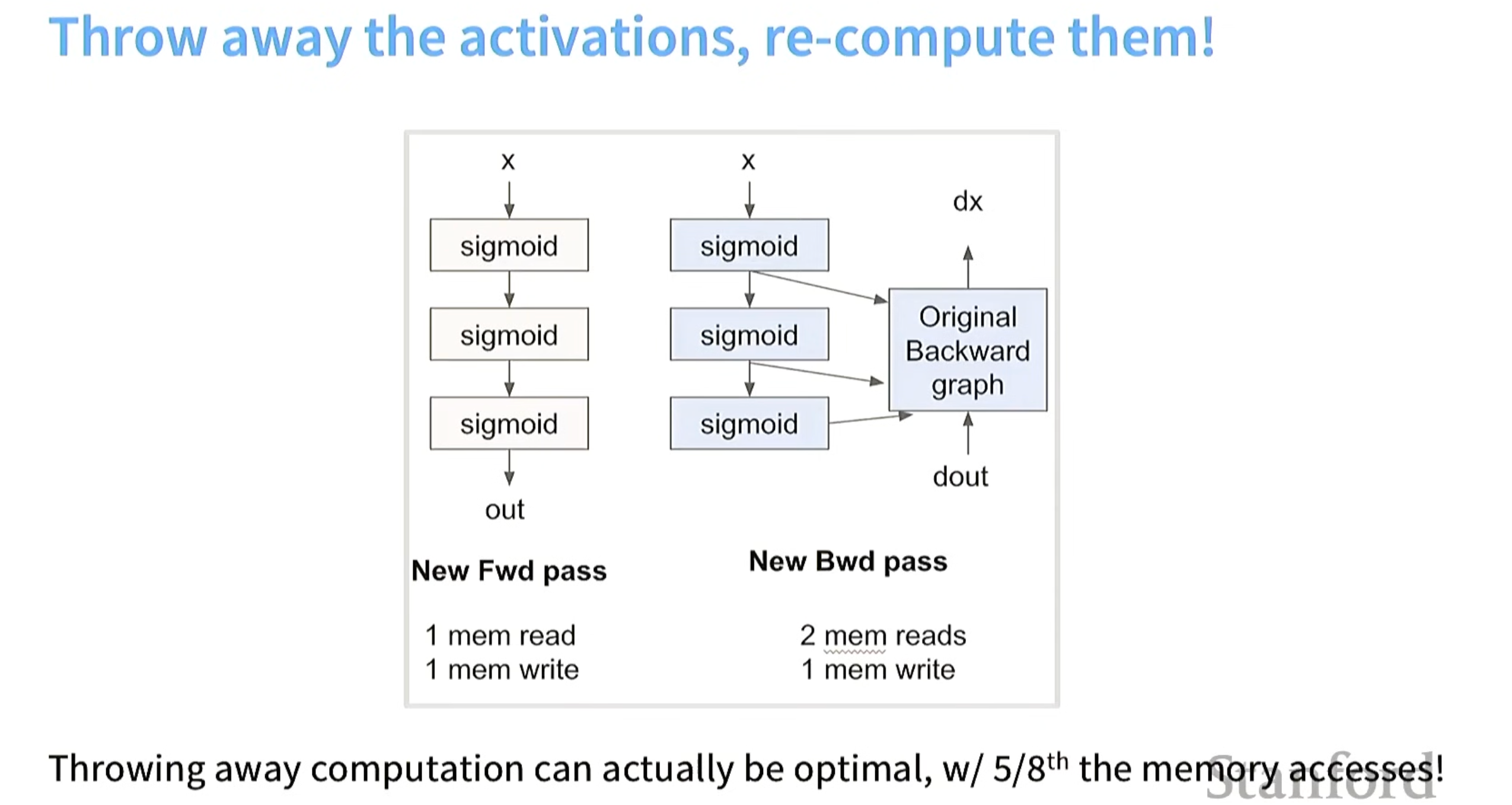
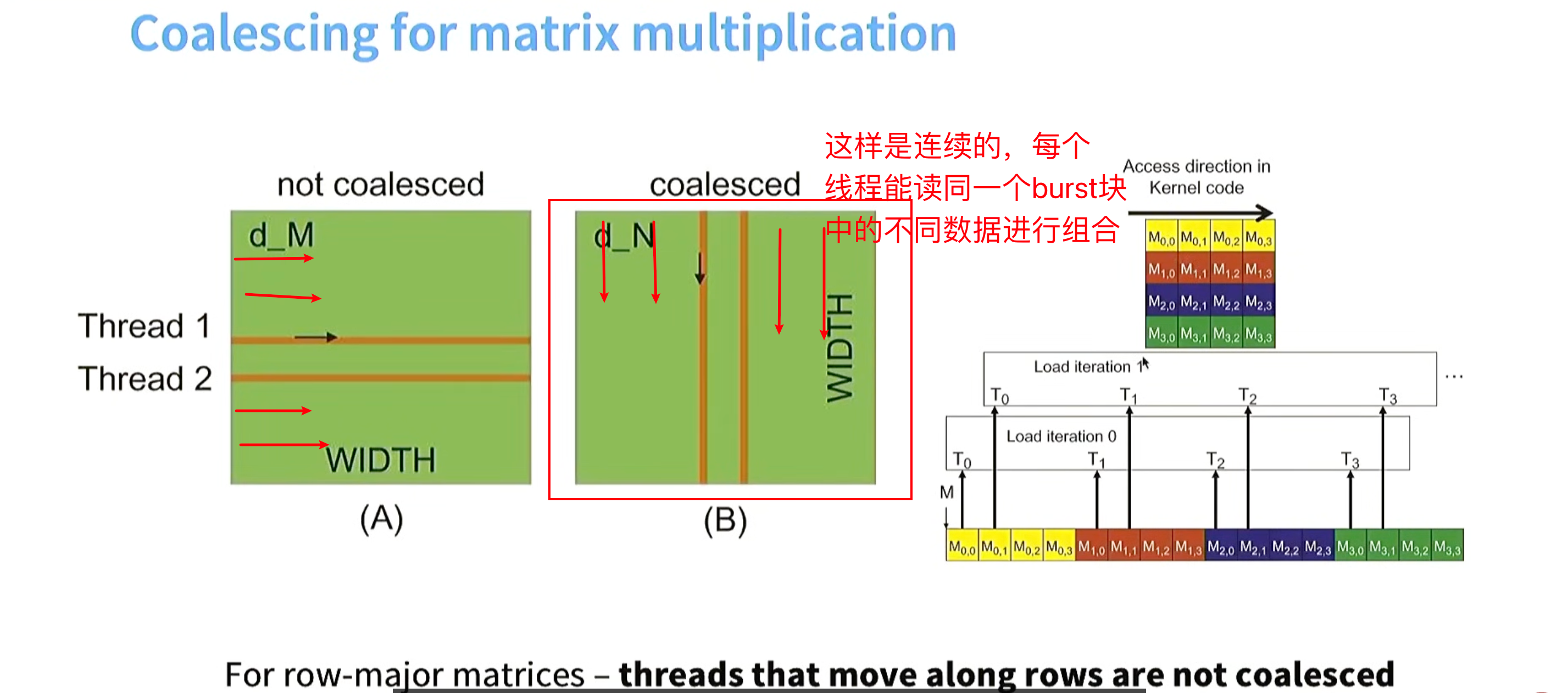
技巧4. memory coalescing(内存合并) ,突发模式(burst mode) 这是硬件层面的优化
当读内存中的一个值的时候,你读到的不仅只是你要的那个值,实际上读到的是跟这个值相连的一个burst section内存。gpu觉得后面可能也需要这些值。
一个warp(32线程)可以一次获取4个字节(一个burst section)而不是一个字节一个字节的读,吞吐量提升4倍。

解释:一个 Warp 的 32 个线程,在同一时刻访问的地址是否连续。---这里列是连续的
在 row-major 矩阵中,真正按列访问(m00, m10, m20)是非合并的 ;
所谓"列是 coalesced",指的是 warp 的线程索引对应列下标,使同一时刻访问的是一行中连续的元素。
在 CUDA 里,"连续不连续"不是看一个线程怎么走,而是看 一个 warp 在同一拍读的地址是不是连续 ;
在 row-major 矩阵中,让 warp 的线程对应列索引,才能触发 coalesced access。
如果warp中线程索引按行进行,每个线程读的都是不同burst section 内存不连续
如果warp中线程索引按列进行,每个线程读的都是同一个burst section中的不同元素,内存连续
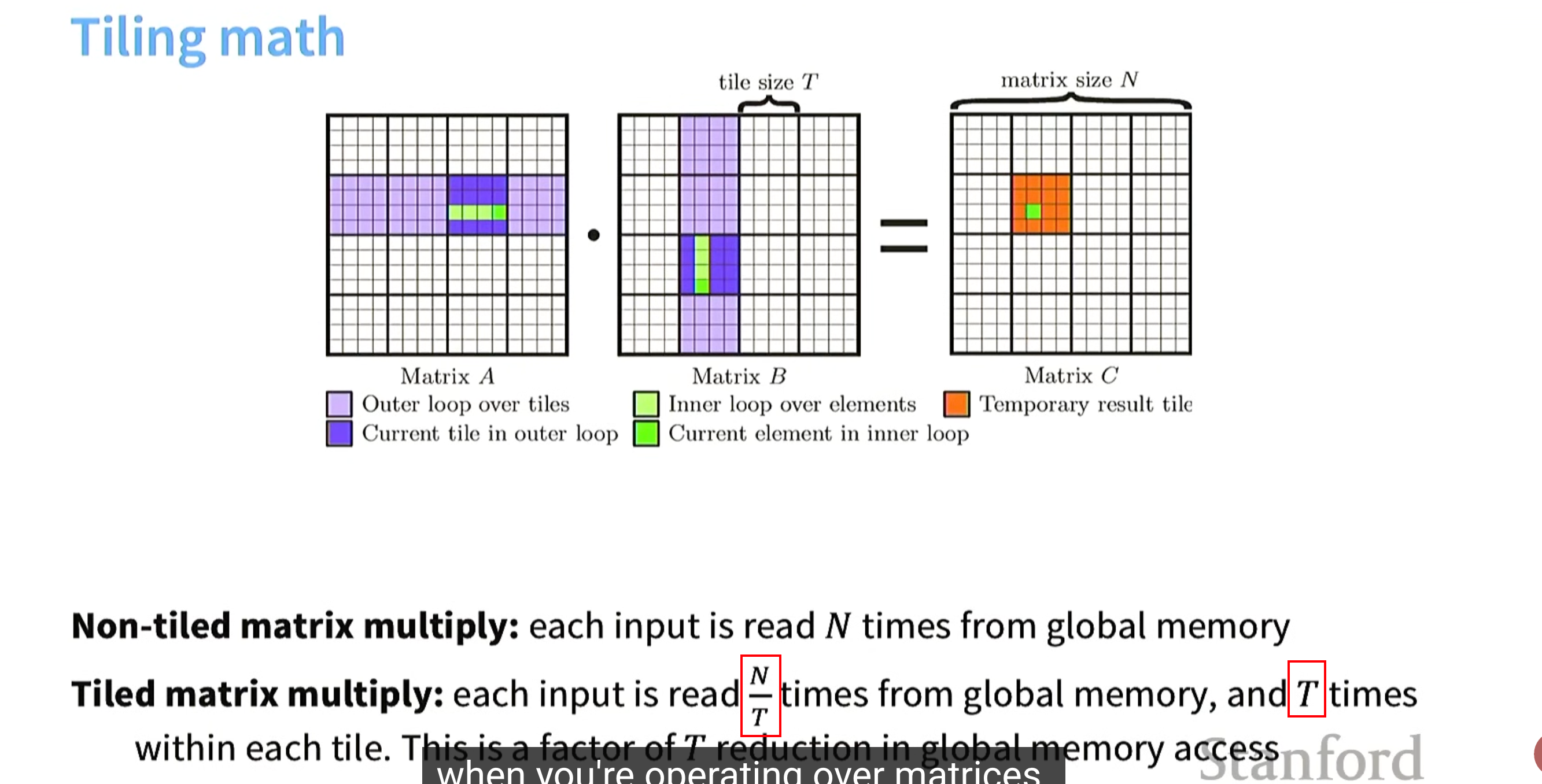
技巧5 分块( Tiling )
为了最小化内存占用,将事物组合到一起。
问题如下:

我们能否避免过多的全局内存读写?
Tiling解决方案:从全局内存 加载一部分数据(尽可能多)到 共享内存中(加载到时候可以按列索引 进行内存连续),共享内存进行运算。

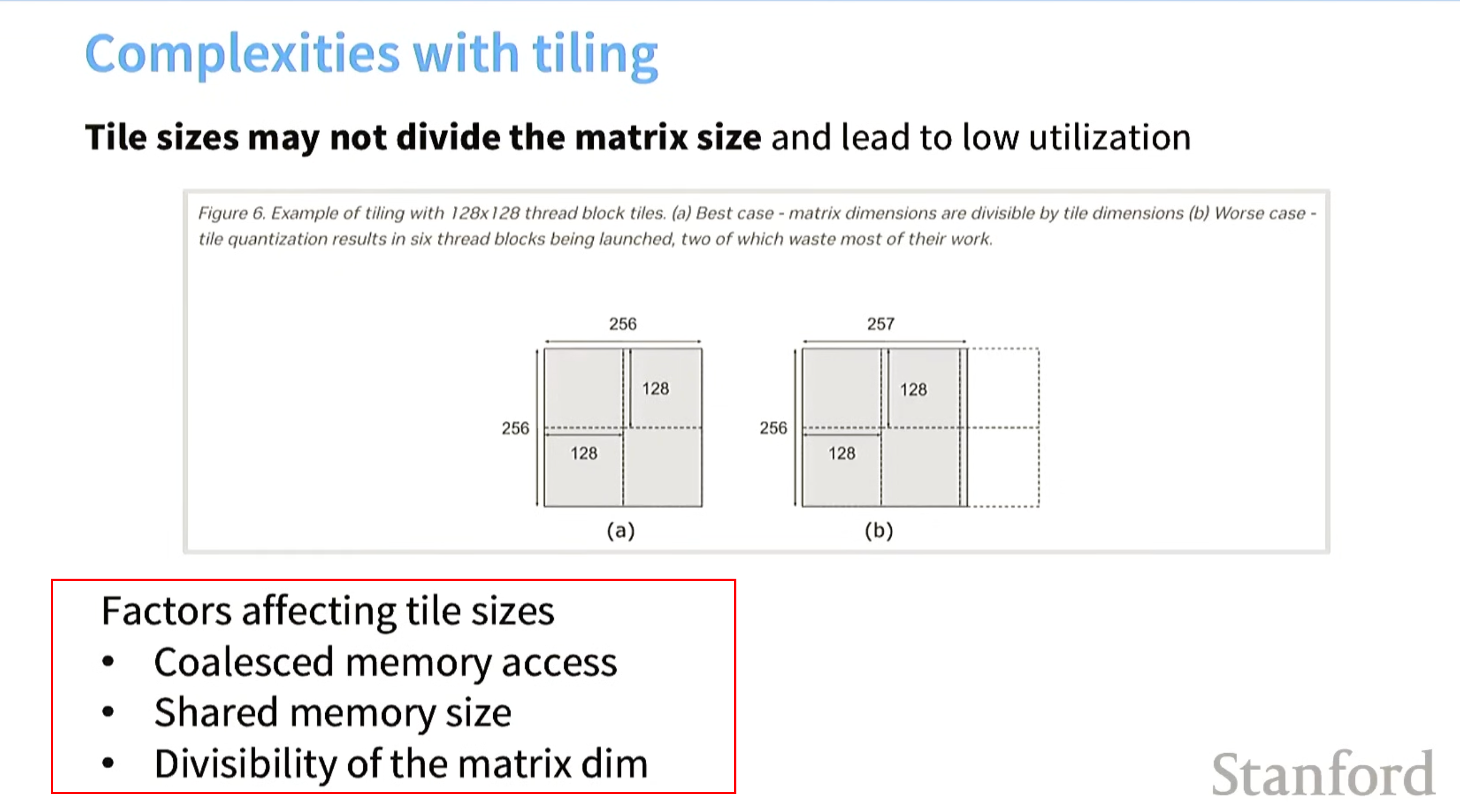
tile的复杂之一 设置tile_size
设置tile size应该考虑几个因素如下
1 连续内存访问 memory coalescing
2 不得超过共享内存大小
3 矩阵的大小 / tile_size 尽可能能整除 (不会陷入到sm未充分利用的情况)
tile的复杂之二 memory alignment(内存对齐)
问题:加上在algned layout的每个行多加一个元素,成了unaliged layout,继续回导致内存访问量double。
解决:对此进行padding 避免内存访问double
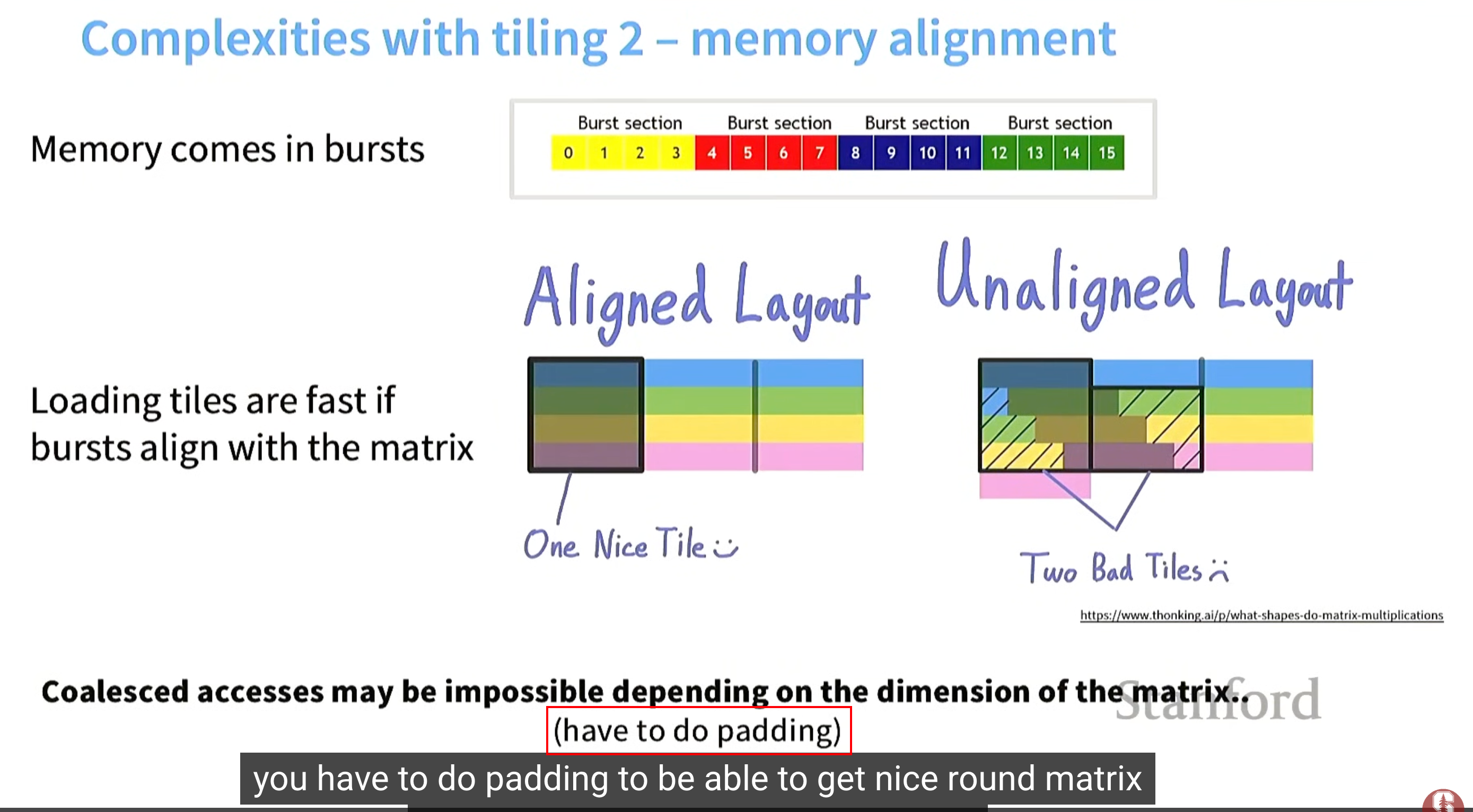
总结-分析曲线图
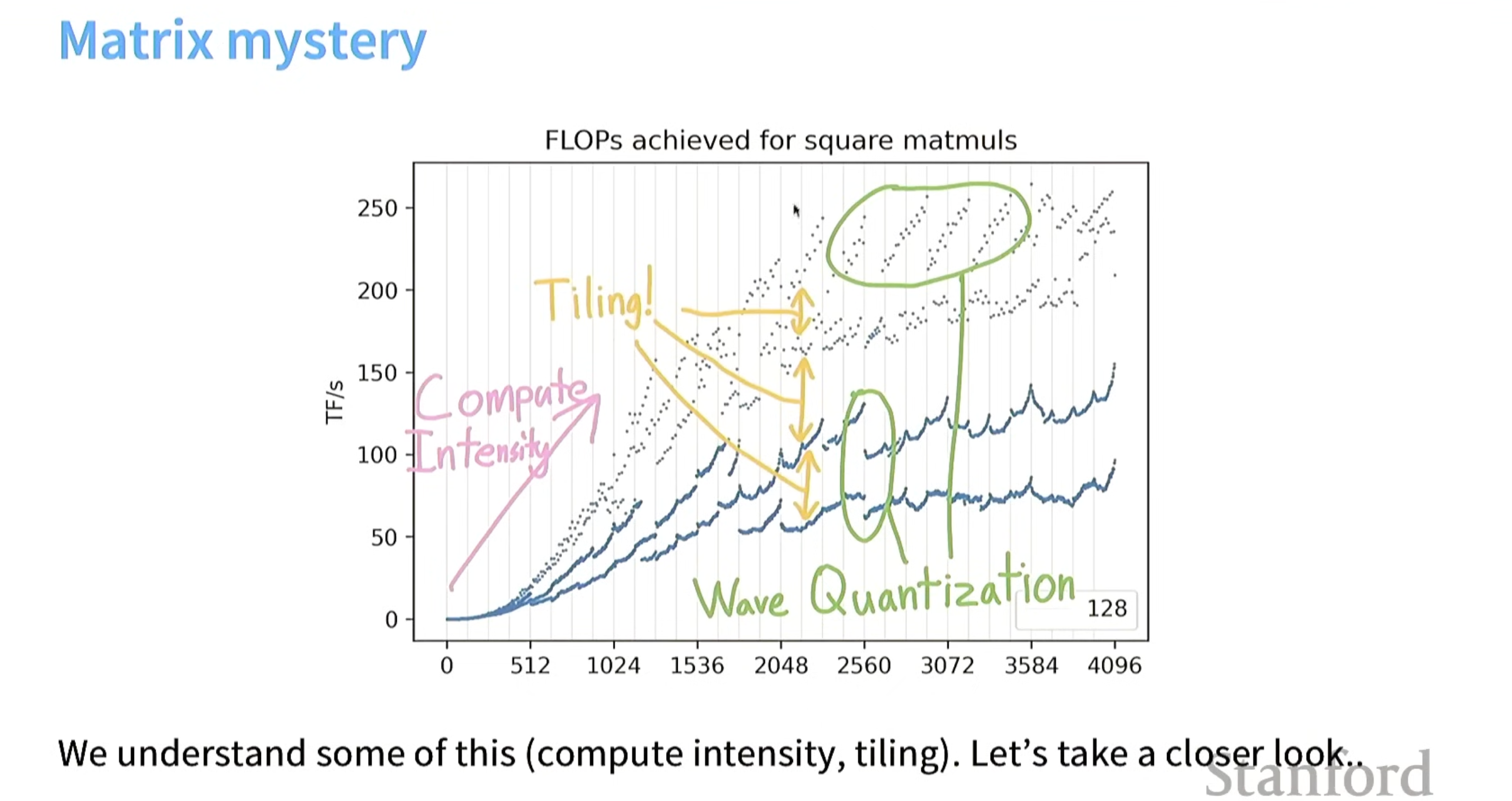
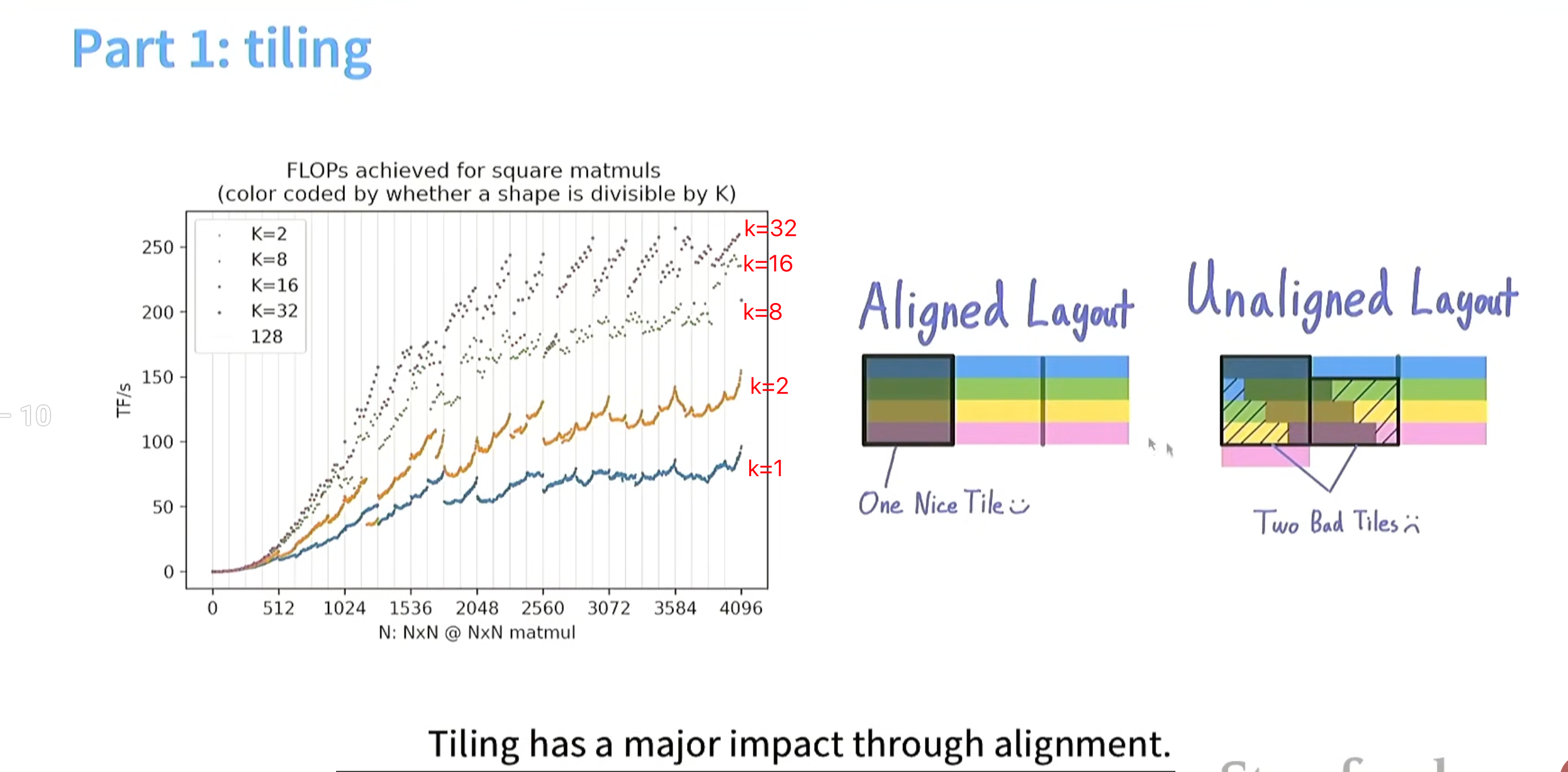
当k=1,k=2时 读tile 没有很好的办法用 burst section对齐,故内存访问占据更多时间,会造成计算量跟不上读的速度。
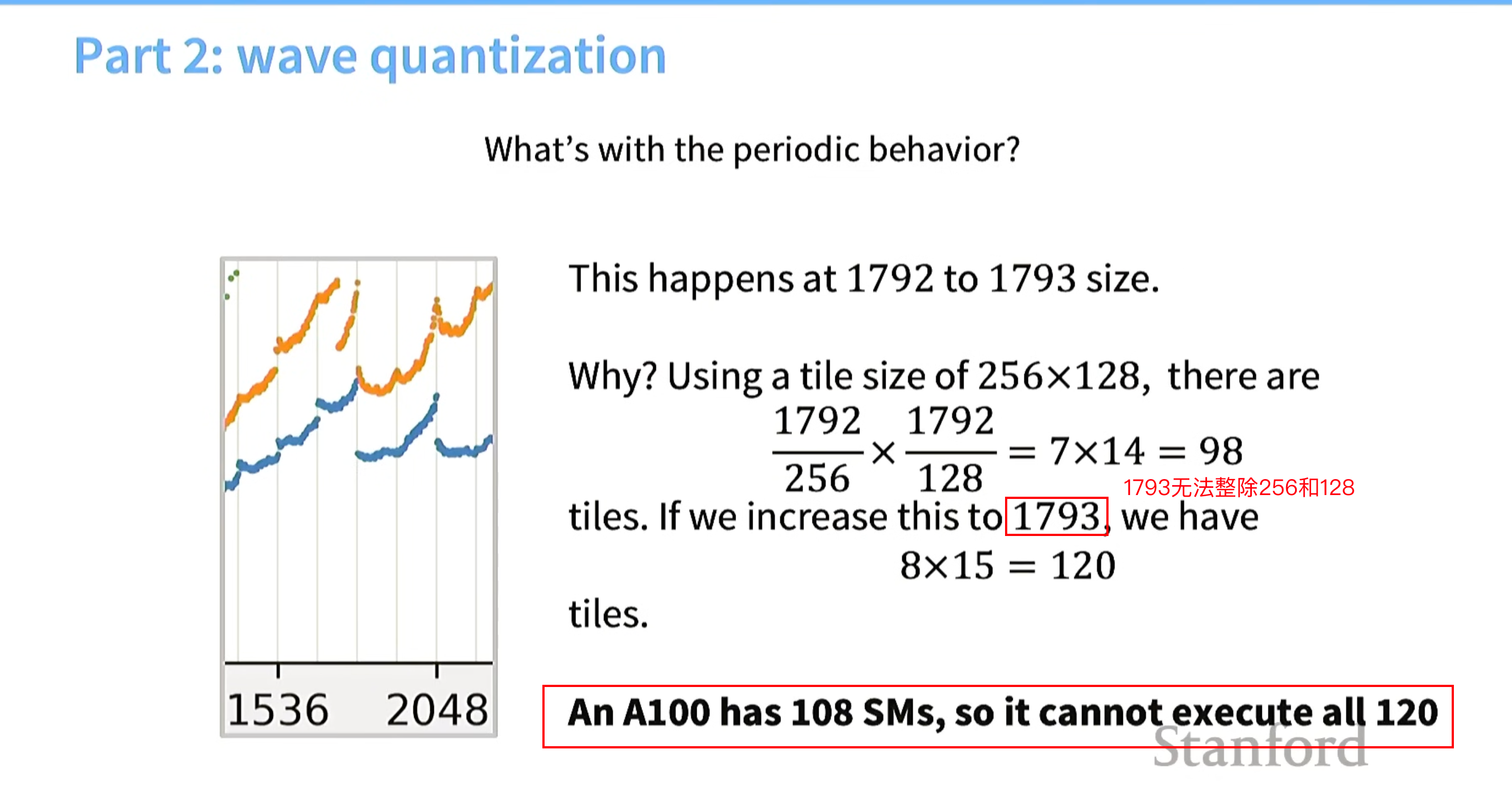
为什么矩阵维度从1792 升到1793 ,计算性能下降很多?
不能整除tile的行列数,且tile个数超过了a100的sms数
从各个部分去分析,应该怎么做
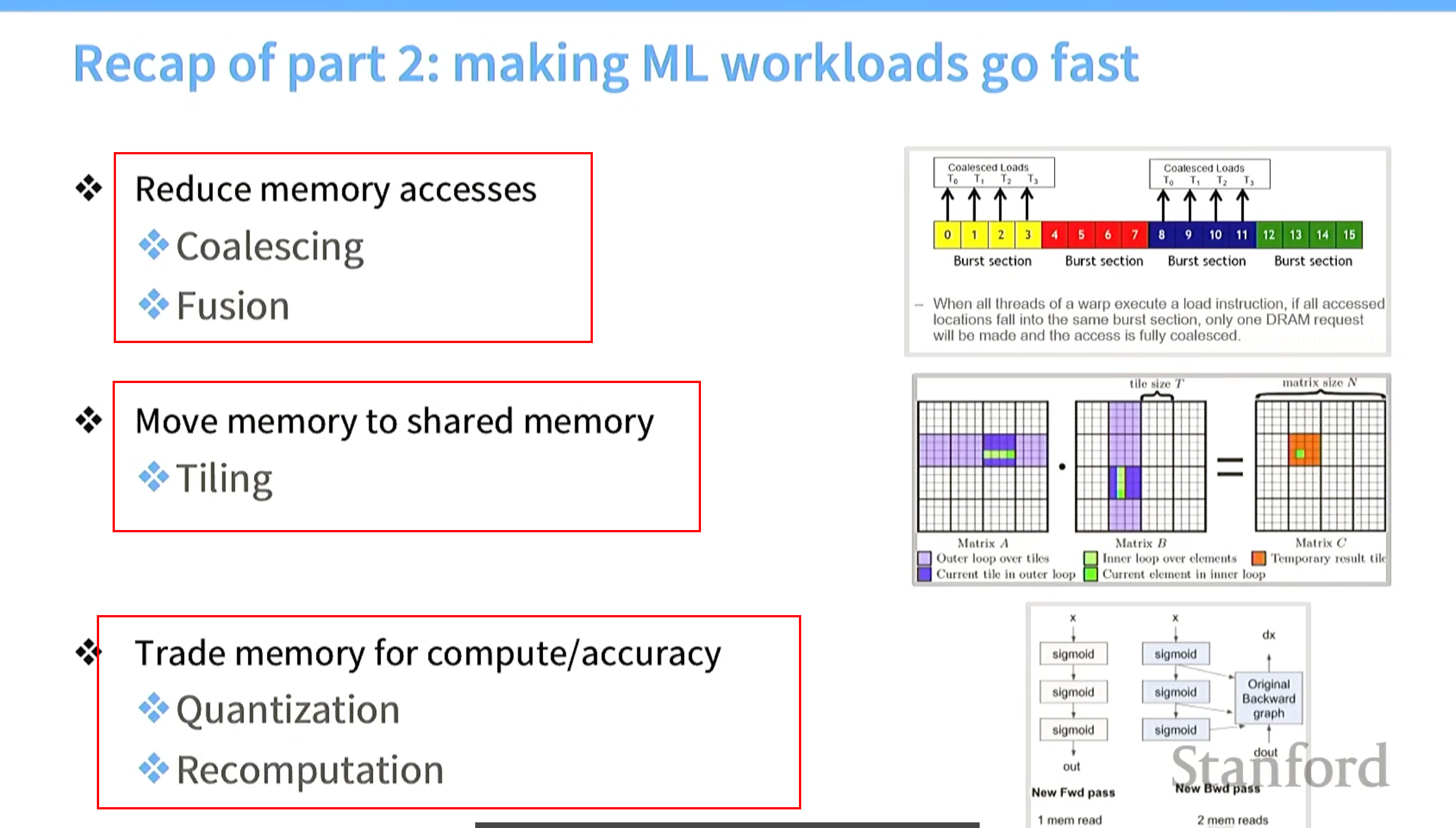
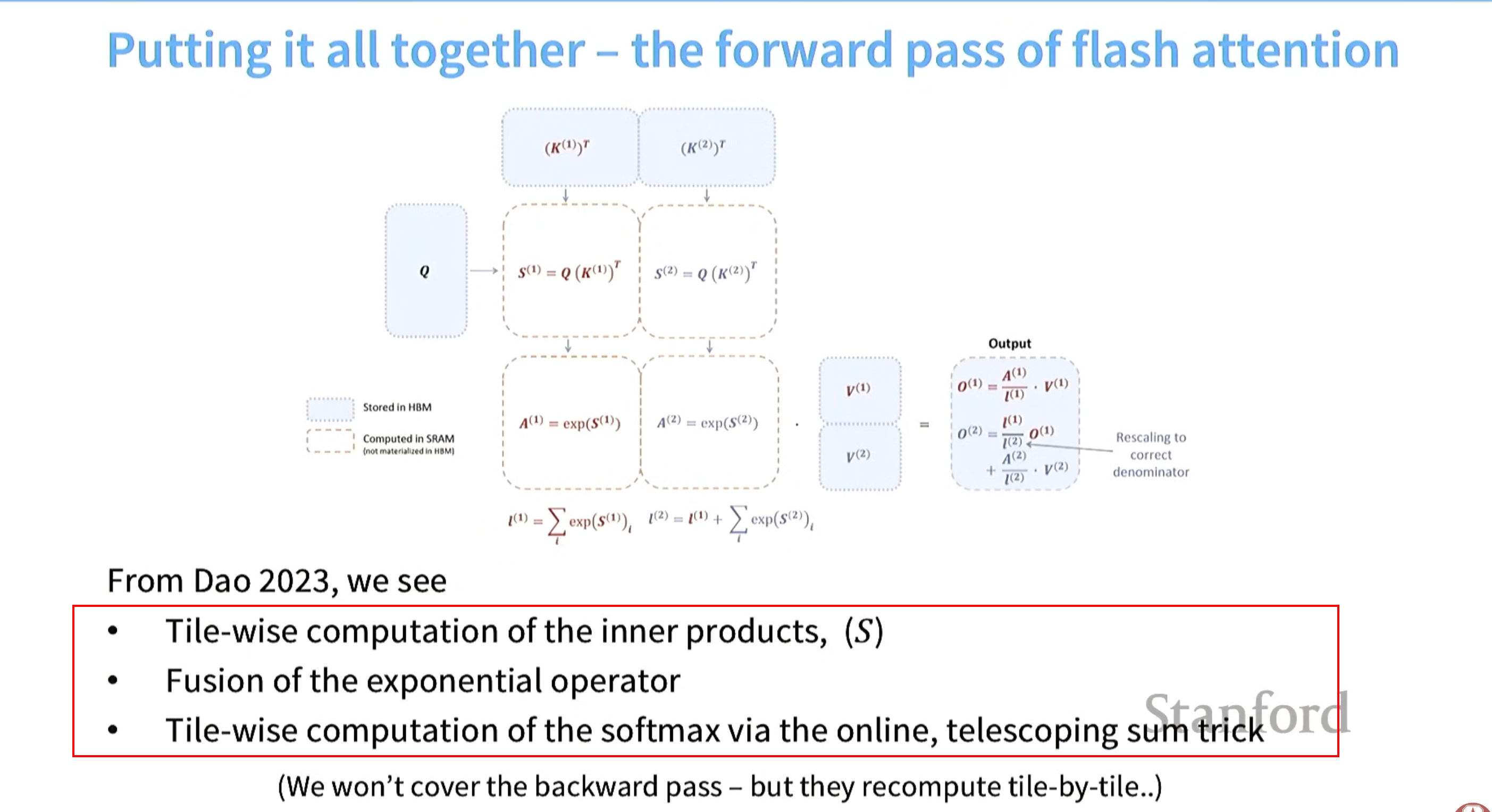
根据所学理解flashattention
一句话:用了分块(tiling)和recomputation,用算子融合(fusion)进行了在线softmax计算。
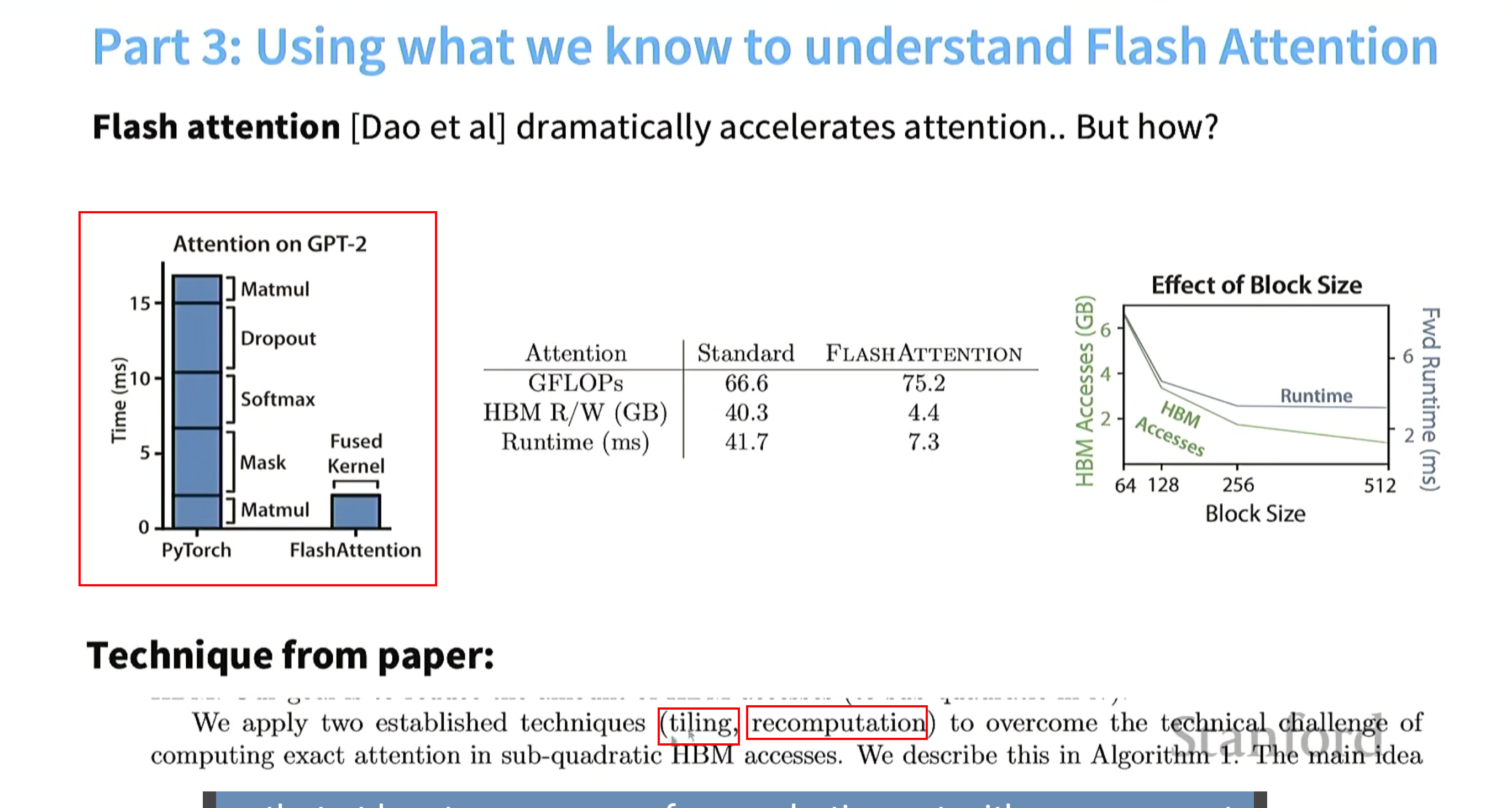
标准attention计算流程如下:
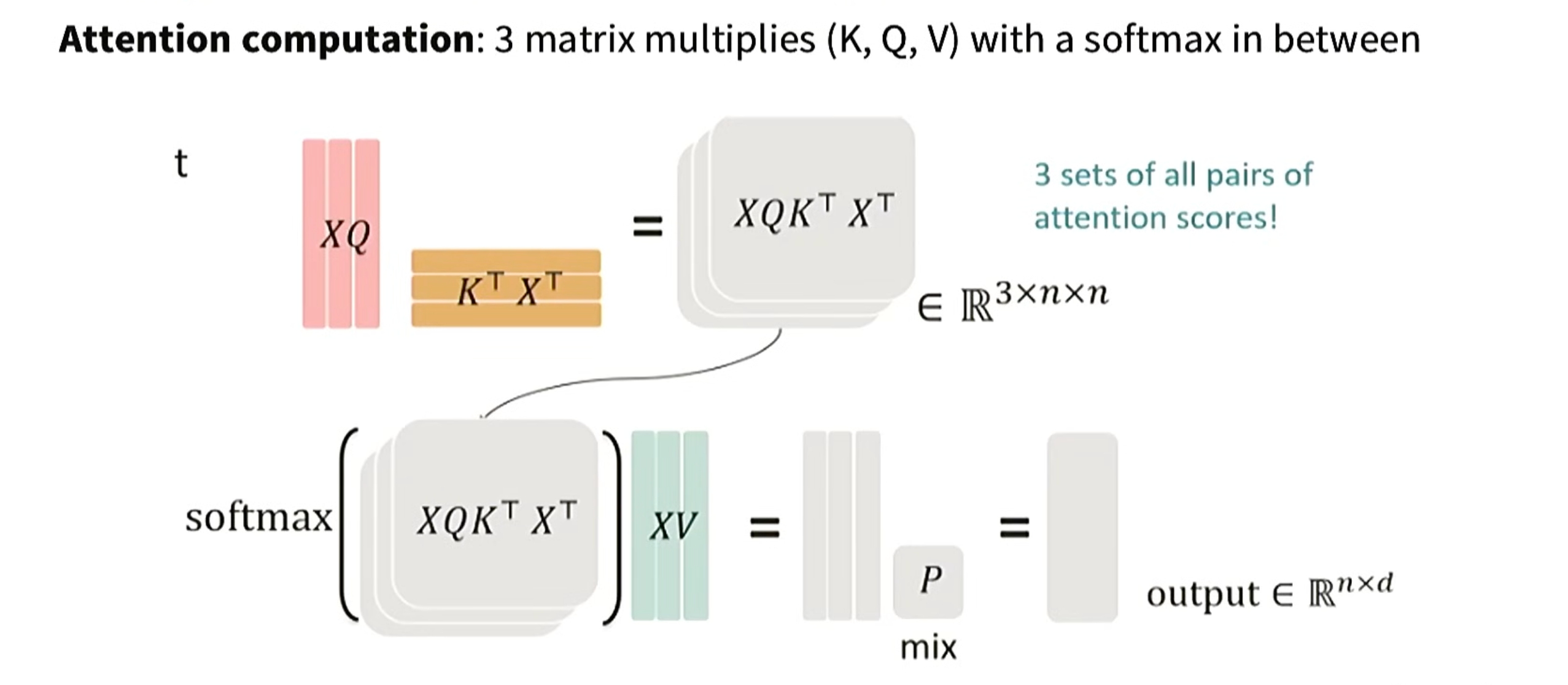
flashattention tiliing流程如下:
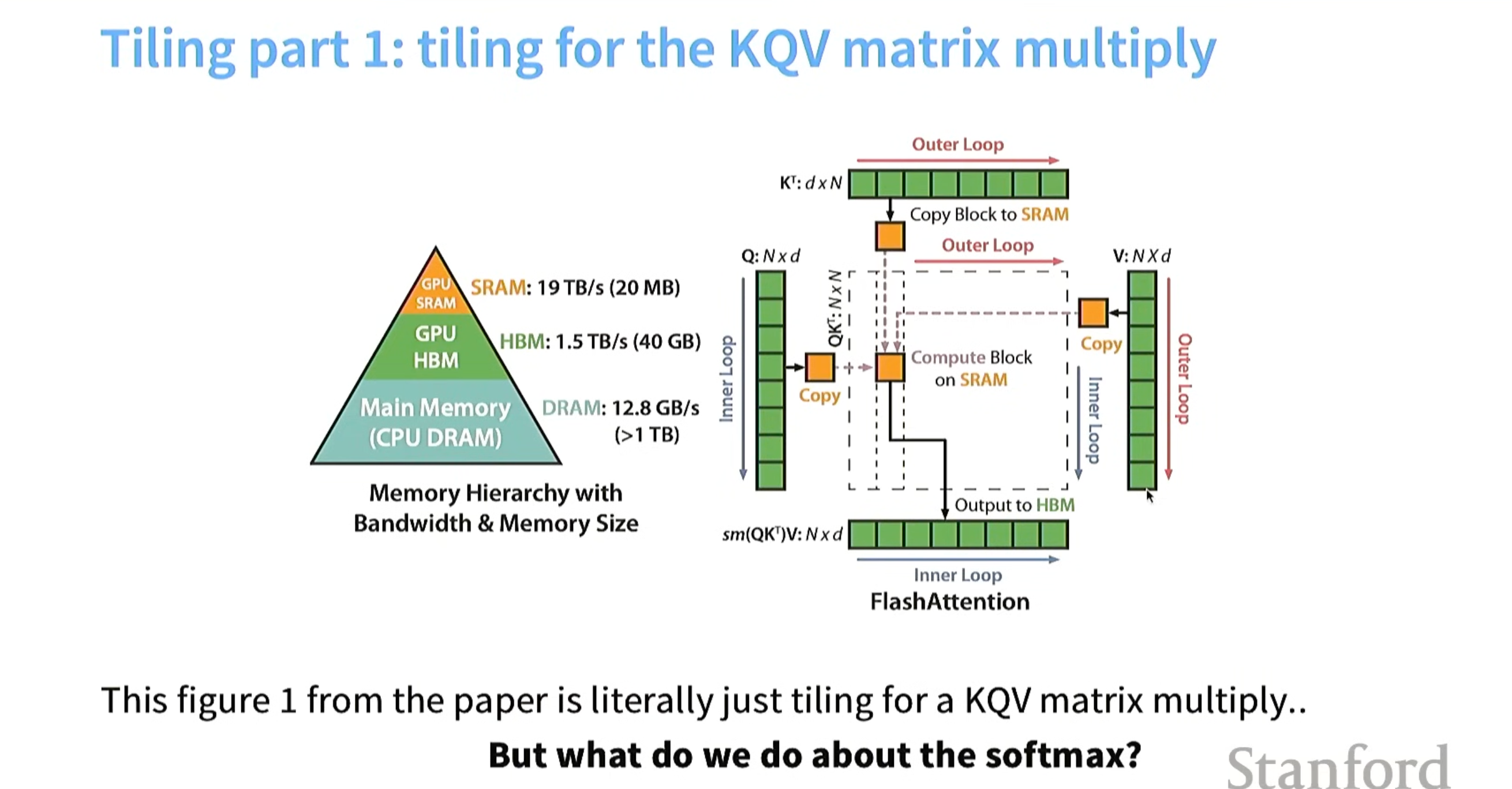
flashattention softmax流程如下:

flashattention 代码演示
py
import numpy as np
def flash_attention_single_query_debug(Q, K, V):
m = -np.inf # running max:当前看到的最大 Q·K
d = 0.0 # running sum:∑ exp(score - m)
o = np.zeros(V.shape[1]) # running output numerator:∑ exp(score - m) * V
print("=" * 100)
print(f"Query Q = {Q}")
print("解释:我们要计算 Softmax(QK^T) @ V")
print(" 即 O = (∑ exp(Q·K_j) * V_j) / (∑ exp(Q·K_j))")
print("=" * 100)
for j in range(K.shape[0]):
score = np.dot(Q, K[j]) # Q · K_j
# 新的最大值(数值稳定关键)
m_new = max(m, score)
# 如果 max 变大,旧结果要整体缩放
scale = np.exp(m - m_new)
# 当前项在新 max 下的指数值
exp_score = np.exp(score - m_new)
# 更新 softmax 分母
d_new = d * scale + exp_score
# 更新 softmax 分子(带 V)
o_new = o * scale + exp_score * V[j]
print(f"[Step {j}] 处理第 {j} 个 Key-Value")
print(f"K[{j}] = {K[j]}")
print(f"V[{j}] = {V[j]}")
print(f"score = Q · K[{j}] = {score:.6f}")
print(f"\n【数值稳定处理】")
print(f"之前最大值 m_prev = {m:.6f}")
print(f"当前 score = {score:.6f}")
print(f"新的最大值 m_new = max(m_prev, score) = {m_new:.6f}")
print(f"\n【指数修正】")
print(f"scale = exp(m_prev - m_new)")
print(f" = exp({m:.6f} - {m_new:.6f})")
print(f" = {scale:.6e}")
print(f"exp(score - m_new)")
print(f"= exp({score:.6f} - {m_new:.6f})")
print(f"= {exp_score:.6e}")
print(f"\n【分母更新(Softmax sum)】")
print(f"d_new = d_prev * scale + exp(score - m_new)")
print(f" = {d:.6e} * {scale:.6e} + {exp_score:.6e}")
print(f" = {d_new:.6e}")
print(f"\n【分子更新(Softmax * V)】")
print(f"o_new = o_prev * scale + exp(score - m_new) * V[{j}]")
print(f" = {o} * {scale:.6e} + {exp_score:.6e} * {V[j]}")
print(f" = {o_new}")
print("-" * 100)
m, d, o = m_new, d_new, o_new
O = o / d
print("\n✅ Final Output")
print("O = o / d")
print(f" = {o} / {d:.6e}")
print(f" = {O}")
print("=" * 100)
return O
# 测试用例1
Q = np.array([1.0])
K = np.array([[5.0], [1.0], [0.0]])
V = np.array([[10.0], [1.0], [1.0]])
flash_attention_single_query_debug(Q, K, V)