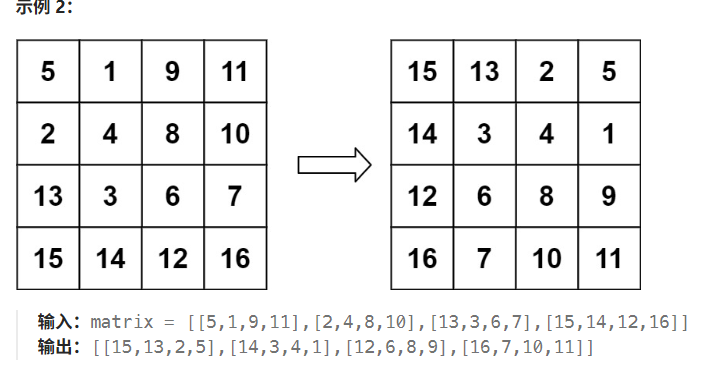
力扣---leetcode48

力扣---leetcode48题,旋转图像:给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在**原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

---

本文使用的方法（对角线翻转 + 左右翻转）是解决这道题最直观、最不容易出错的方法。它利用了矩阵变换的数学性质。

下面我通过数学原理 、图解步骤 和代码细节三个方面为你详细拆解。

---

1. 数学原理

我们要实现的是：坐标 (i, j) 的元素，旋转 90 度后，应该去哪里？

根据坐标变换公式，顺时针旋转 90 度后的位置是： (j, n - 1 - i) 。

直接实现这个变换比较复杂，但我们可以将其分解为两步简单的几何变换：

1. 主对角线翻转（矩阵转置）：
   • 将 (i, j) 变为 (j, i) 。
   • 此时，行变成了列。
2. 左右镜像翻转：
   • 将 (j, i) 变为 (j, n - 1 - i) 。
   • 此时，每一行的元素顺序颠倒。

结论： (i, j) \\xrightarrow{转置} (j, i) \\xrightarrow{左右翻转} (j, n - 1 - i) 。这刚好完成了顺时针 90 度旋转。

---

2. 图解步骤（以 3x3 矩阵为例）

假设原始矩阵如下：

1  2  3
4  5  6
7  8  9

第一步：沿主对角线翻转

主对角线就是从左上角到右下角的这条线（1, 5, 9）。我们将对角线两侧的元素进行两两交换：

• 2 和 4 交换
• 3 和 7 交换
• 6 和 8 交换

变化后的矩阵：

1  4  7
2  5  8
3  6  9

此时观察：原来的第一行 1,2,3 变成了现在的第一列。

第二步：每一行左右镜像翻转

对每一行进行反转（Reverse）：

• 第一行 1, 4, 7 变成 7, 4, 1
• 第二行 2, 5, 8 变成 8, 5, 2
• 第三行 3, 6, 9 变成 9, 6, 3

变化后的矩阵：

7  4  1
8  5  2
9  6  3

结果完成！这正是原矩阵顺时针旋转 90 度后的样子。

---

3. 代码实现细节（Java 示例）

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 1. 沿主对角线翻转 
        // 注意：j 从 i + 1 开始，只处理右上半部分，避免重复交换
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        // 2. 每一行进行左右翻转 
        // 每一行只遍历到一半 (n / 2)
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n / 2; j++) {
                int temp = matrix[i][j];
                // 将左边的数与右边对称位置的数交换
                matrix[i][j] = matrix[i][n - 1 - j];
                matrix[i][n - 1 - j] = temp;
            }
        }
    }
}

---

4. 关键点总结（面试常考）

Q1：为什么第一步循环里 j 要从 i + 1 开始？

如果 j 从 0 开始遍历到 n，当你处理到 matrix[1][0] 时，它会和 matrix[0][1] 交换；但当你处理到 matrix[0][1] 时，它又会和 matrix[1][0] 交换回去。结果就是矩阵没变。

主对角线上面的元素 → 严格满足 行号 < 列号（i < j）

主对角线下面的元素 → 严格满足 行号 > 列号（i > j）

所以我们只遍历"右上三角形"的区域，把它们和"左下三角形"对应的位置交换。

Q2：如果是逆时针旋转 90 度怎么办？

有两种常见的分解方法：

• 方案 A： 先左右翻转，再沿主对角线翻转。
• 方案 B： 先沿主对角线翻转，再上下翻转。

Q3：这种方法的时空复杂度？

• 时间复杂度： O(N\^2) 。转置需要遍历约 N\^2/2 次，左右翻转需要遍历 N\^2/2 次，总共还是 O(N\^2) 。
• 空间复杂度： O(1) 。所有操作都在原数组上完成，不需要额外空间。暴力方法是 。所有操作都在原数组上完成，不需要额外空间。暴力方法是 。所有操作都在原数组上完成，不需要额外空间。暴力方法是 O(n)

为什么推荐这个方法？

在面试中，直接写"四数交换"的公式（方法二）非常容易记错下标（比如把 n-1-i 写成 n-i），一旦写错，调试会非常痛苦。而方法一步骤清晰，每一块逻辑都很简单，极难出错，是代码鲁棒性（Robustness）最高的选择。

鲁棒性 （Robustness）是计算机科学中一个非常重要的概念，它是英文 Robust 的音译（也有人称之为"健壮性"或"稳定性"）。