深度解析：词向量与自注意力机制

1.词的表示方式

词的表示即为将输入的语句转换为计算机可以处理的数字形式。

1.1 独热编码（One-hot Encoding）

独热编码是一种最简单、最基础的将离散型数据（特别是分类数据）转换为数值形式的方法。

假设词汇表含有w个不同的词，则会产生w维的向量；
每个词都会被表示成长度为w的向量；
对于特定的某个词，只有其索引位置为1，其余位置均为0；

无法表示语义之间的关系，完全丢失了词语之间的语义信息。

1.2 词向量（Word Embedding）

为解决独热编码的缺陷，词向量采用相对低纬、稠密、连续的向量来表示一个词，并且让这个向量能够捕捉词语的语义和语法信息。

稠密低纬：维度通常在50-300之间；
蕴含语义：语义相似的词，其向量在空间中的距离也相近（余弦相似度等度量）；

静态词向量表示中一个词只有一个向量，无法处理一词多义（多义词）问题。

2.自注意力

自注意力的关键在于key,query,value同源，来自于同一个x。计算过程：

①通过三个矩阵生成Q,K,V，其余步骤与注意力机制做法相同。

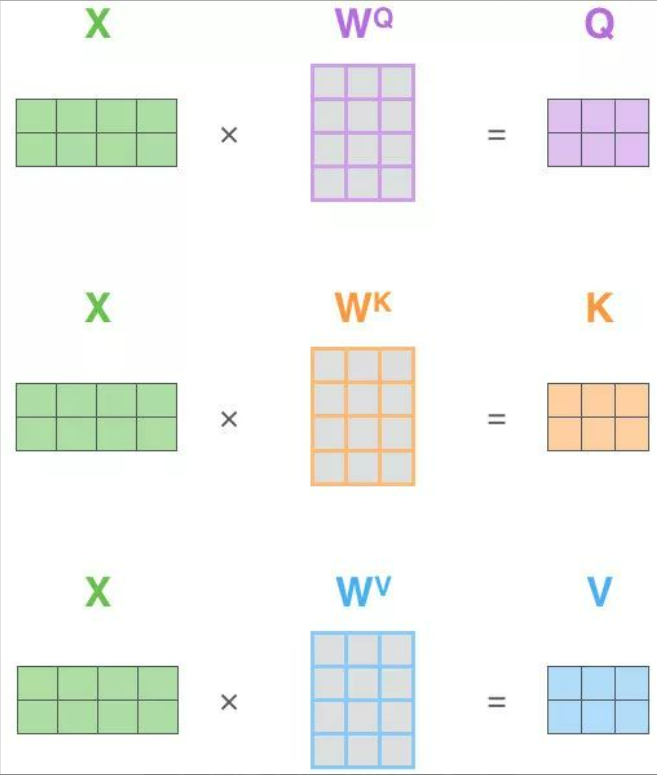
②计算注意力分数

③缩放与归一化

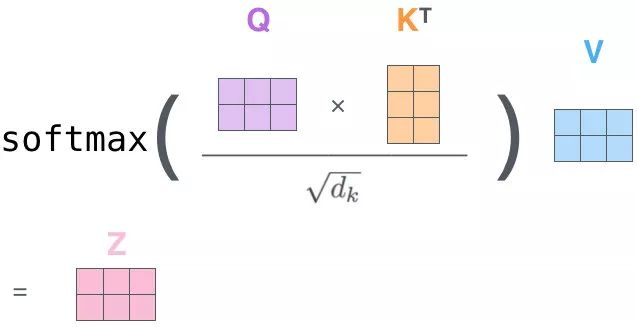
自注意力（Self-Attention） 的核心目标：让模型在处理一个词时，能够有选择地关注输入序列中的其他部分，从而获得该词在当前上下文中最准确的表示。
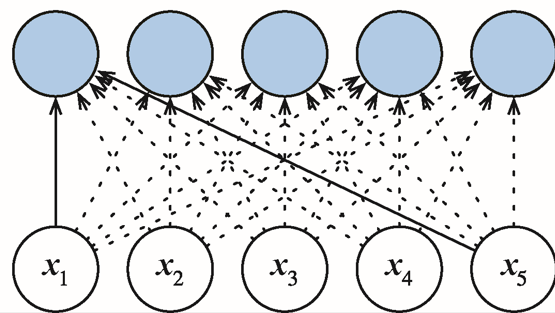自注意力

在自注意力机制中，每个词元都通过注意力直接连接到任何其他词元，具有并行计算 的优势，并且自注意力的**最大路径长度最短，**在长序列中计算缓慢。

3.位置编码

自注意力机制有一个关键特性就是排列不变性，他没有记录位置信息，因此在纯自注意力中"我爱你"和"你爱我"的词对关系是一致的。但是我们又明白"我爱你" ≠ "你爱我"，因此需要引入位置。

（1）基本思想：给每个位置的词向量添加一个位置信号，表明：

该词在序列中的绝对位置；
词与词之间的相对位置关系。

（2）假设长度为n的序列是，使用位置编码矩阵 P 来输出 X+P 作为自编码输入。

对于位置 pos 和维度 i ：

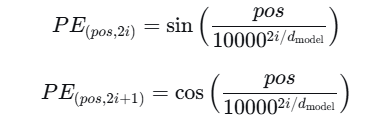
以我爱你中的"爱"为例：
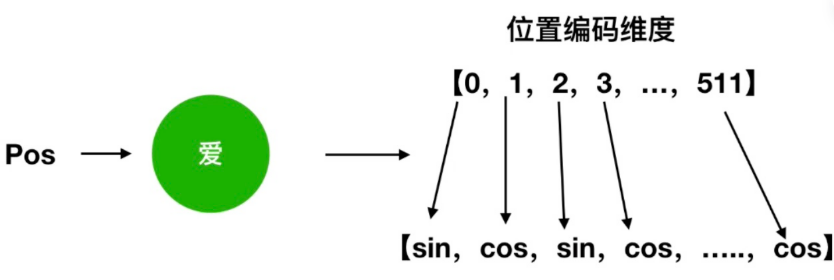位置编码

自编码输入：

（3）位置编码数学性质

唯一性：每一个位置编码都不同；
有界性：值在 [-1,1] 之间，与词的嵌入匹配；
距离敏感：相近位置编码相似，远离位置编码差异大。

（4）为什么不直接按照位置进行编码 [1,2,3,4....]

直接使用位置索引：数据差异范围太大，比如100比1大百倍；

归一化位置：长序列中相邻位置差异太小，0.99与1.00；

二进制编码：离散变化，无法平滑表示相似位置；

（5）基于正弦函数与余弦函数的固定位置编码借助三角函数性质可以实现相对位置信息。

因此在计算 pos + k 个词的位置编码时，可以得到：

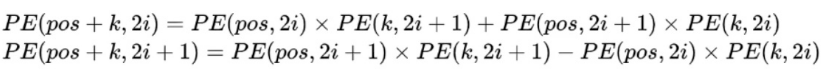
可以看出，对于 pos + k 位置的位置向量某一维 2i 或 2i + 1 而言，可以表示为 pos 位置与 k 位置的位置向量的 2i 与 2i + 1 维的线性组合，在线性组合中蕴含着相对位置信息。

4.代码示例

位置编码类的实现：

python 复制代码

class PositionalEncoding(nn.Module): #     
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000): # 最大序列长度
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)  # dropout层，用于防止过拟合
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

位置嵌入矩阵P中，行代表词元在序列中的位置，列代表位置编码的不同维度

python 复制代码

encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
         figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])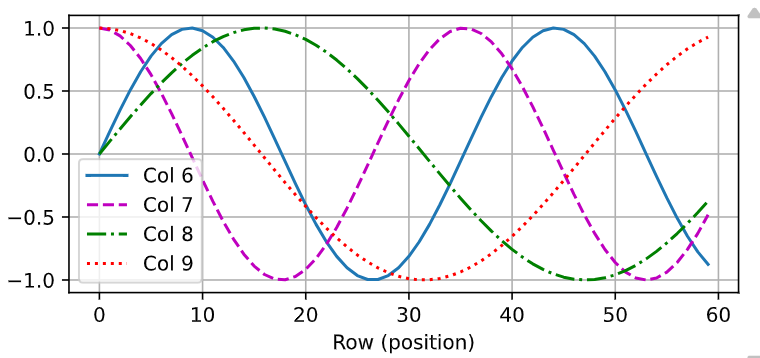

可以看到位置嵌入矩阵第6列与第7列的频率高于第8列和第9列；第6列与第7列之间的偏移，第8列和第9列之间的偏移是因为正弦函数和余弦函数的交替。

5.小结

在自注意力池化层中，查询、键和值都来自于同一组输入；
卷积神经网络（CNN）和自注意力都具有并行计算的优势，而且自注意力的最大路径长度最短。但是其计算复杂度是关于序列长度的平方，因此在很长的序列中计算十分慢；
为了使用序列的顺序信息，可以通过在输入表示中添加位置编码，来注入绝对的或相对的位置信息。