动态规划进阶：简单多状态模型

目录

• 动态规划进阶：深度解析序列决策与状态机模型
• • [一、 "打家劫舍"模型：状态拆分的起点](#一、 “打家劫舍”模型：状态拆分的起点)
  • • 题目：198.打家劫舍
    • 题目：213.打家劫舍II
    • 题目：740.删除并获得点数
  • [二、 "买卖股票"模型：多状态机的演进](#二、 “买卖股票”模型：多状态机的演进)
  • • 题目：309.买卖股票的最佳时期含冷冻期
    • 题目：123.买卖股票的最佳时机III

动态规划进阶：深度解析序列决策与状态机模型

在处理具有复杂限制条件的动态规划问题时，单一的状态定义往往难以涵盖所有决策分支。通过将每一天的局面拆解为多个互斥的快照（States） ，并利用状态机描述其间的转移逻辑，可以有效地消除后效性，使问题迎刃而解。

---

一、 "打家劫舍"模型：状态拆分的起点

这类题目的核心在于处理"相邻元素互斥"的约束。

题目：198.打家劫舍

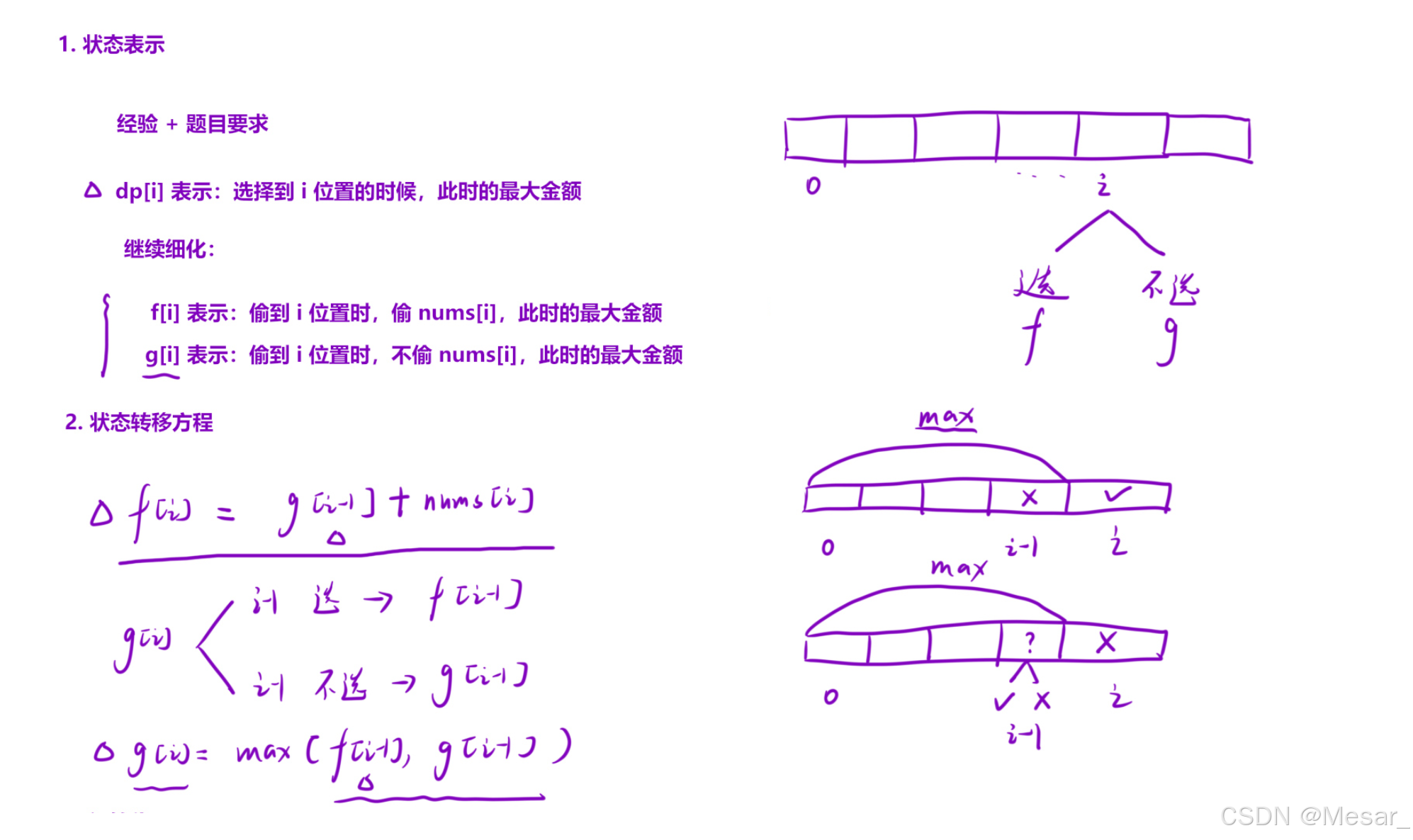
• 状态表示：

• f [ i ] f[i] f[i]：表示偷到第 i i i 个位置时，确定偷 n u m s [ i ] nums[i] nums[i]，此时的最大金额。

• g [ i ] g[i] g[i]：表示偷到第 i i i 个位置时，确定不偷 n u m s [ i ] nums[i] nums[i]，此时的最大金额。

• 状态转移方程：基于"最后一步"的决策逻辑：

• f [ i ] = g [ i − 1 ] + n u m s [ i ] f[i] = g[i-1] + nums[i] f[i]=g[i−1]+nums[i]：若偷当前房，前一间房必须处于"不偷"状态。

• g [ i ] = max ⁡ ( f [ i − 1 ] , g [ i − 1 ] ) g[i] = \max(f[i-1], g[i-1]) g[i]=max(f[i−1],g[i−1])：若不偷当前房，前一间房偷或不偷均可，取最大值即可。

• 初始化 ： f [ 0 ] = n u m s [ 0 ] f[0] = nums[0] f[0]=nums[0]， g [ 0 ] = 0 g[0] = 0 g[0]=0。
  

代码实现：

class Solution 
{
public:
    int rob(vector<int>& nums) 
    {
        //跟按摩师一样
        int n=nums.size();
        vector<int> f(n);
        auto g=f;
        f[0]=nums[0];
        for(int i=1;i<n;++i)
        {
            f[i]=g[i-1]+nums[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        return max(f[n-1],g[n-1]);
    }
};

题目：213.打家劫舍II

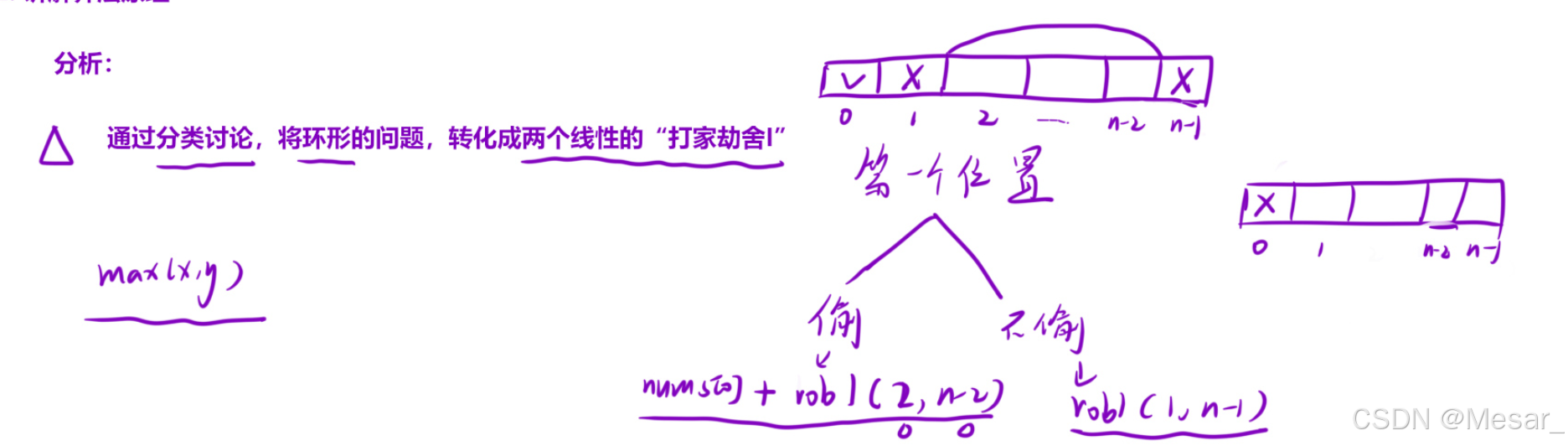
• 核心痛点：第一间房与最后一间房首尾相连，产生约束冲突。
• 化圆为线策略：通过"分类讨论"消除环形约束：
• 情况 A ：不考虑第一间房，在区间 [ 1 , n − 1 ] [1, n-1] [1,n−1] 执行上述逻辑。
• 情况 B ：不考虑最后一间房，在区间 [ 0 , n − 2 ] [0, n-2] [0,n−2] 执行上述逻辑。
• 结论 ：最终结果为 max ⁡ ( 情况 B , 情况 A ) \max(\text{情况 B}, \text{情况 A}) max(情况 B,情况 A)。

代码实现：

class Solution 
{
public:
    int rob(vector<int>& nums) 
    {
    			//处理首位房子后确定进行打家劫舍的区间
        //转化为打家劫舍1（找到可以进行打家劫舍1的区间）
        int n=nums.size();
        return max(nums[0]+rob1(nums,2,n-2),rob1(nums,1,n-1));
    }

    int rob1(vector<int>& nums,int left,int right)
    {
        if(left>right)return 0;
        int n=nums.size();
        vector<int> f(n);
        auto g=f;
        f[left]=nums[left];
        for(int i=left+1;i<=right;++i)
        {
            f[i]=g[i-1]+nums[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        return max(f[right],g[right]);
    }
};

题目：740.删除并获得点数

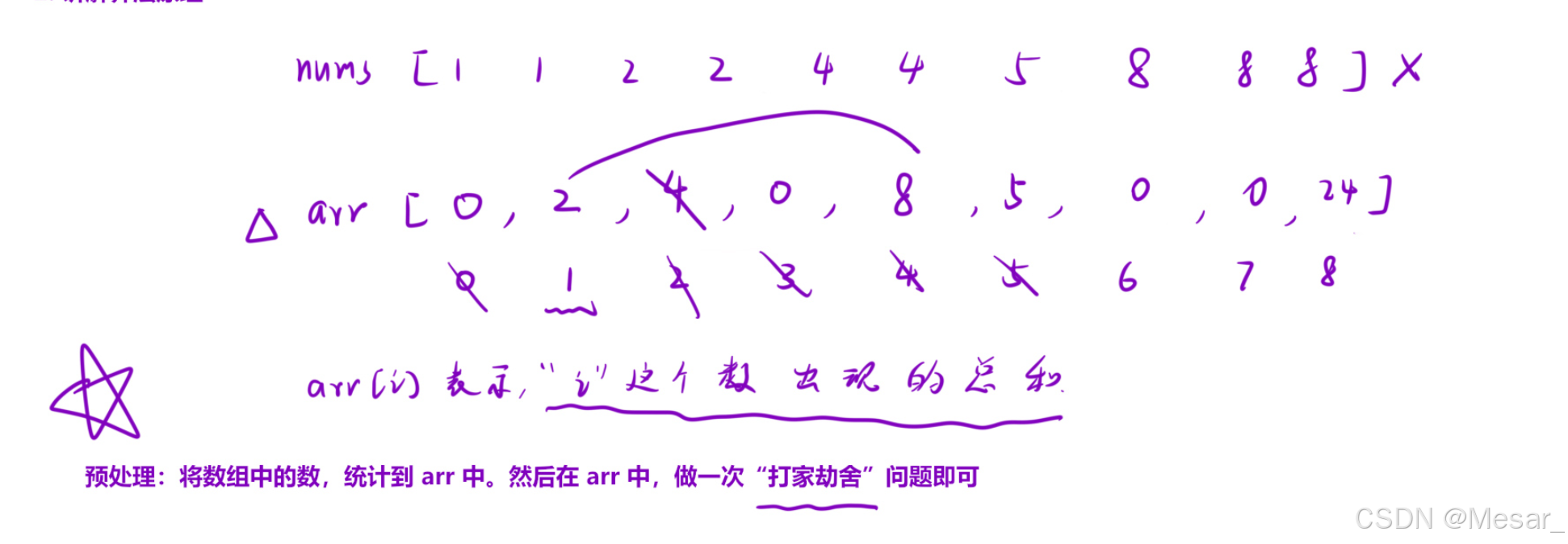
• 转化思维：这道题看似新颖，实则是"打家劫舍"的变体。
• 预处理 ：先统计每个数字出现的总分（点数 = 数字 × \times × 出现次数）。
• 建立映射 ：数字 i i i 的选取会导致 i − 1 i-1 i−1 和 i + 1 i+1 i+1 无法选取，这完全等同于"相邻房屋不能同时偷"的逻辑
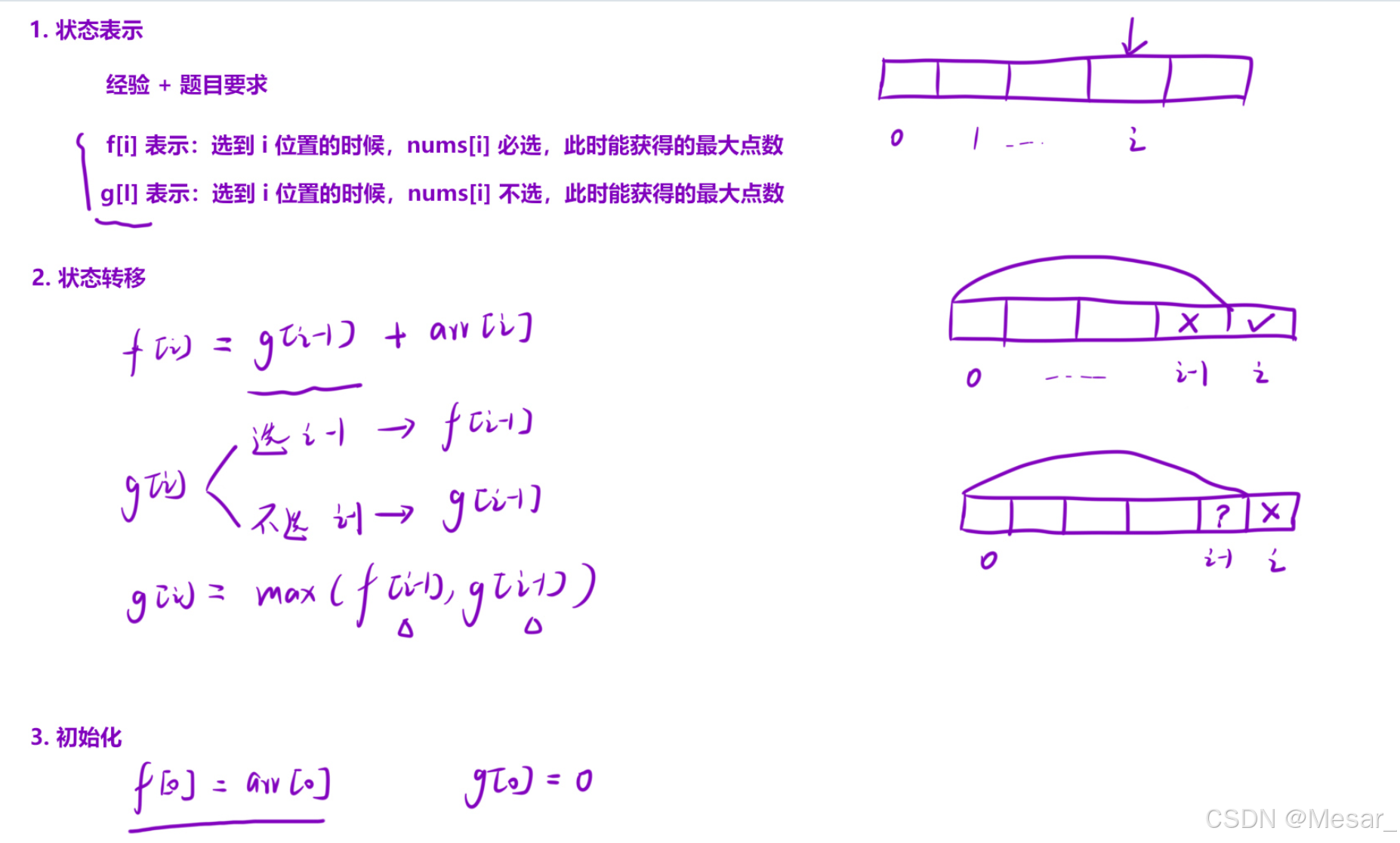
• 解法 ：对统计后的点数数组执行 f [ i ] f[i] f[i] 与 g [ i ] g[i] g[i] 的状态转移。

状态表示及状态转移方程

代码实现：

class Solution 
{
public:
    int deleteAndEarn(vector<int>& nums) 
    {
        sort(nums.begin(),nums.end());
        int n=nums[nums.size()-1]+1;//加上0这个位置
        //将原数组的值累加到v的对应位置，之后就可以转变为打家劫舍
        vector<int> v(n);
        for(int i=0,j=nums[i];i<nums.size();)
        {
            if(nums[i]==j)v[j]+=nums[i++];
            else ++j;
        }

        //打家劫舍
        vector<int> f(n);
        auto g=f;
        f[1]=v[1],g[1]=0;
        for(int i=2;i<n;++i)
        {
            f[i]=g[i-1]+v[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        return max(f[n-1],g[n-1]);
    }
};

---

二、 "买卖股票"模型：多状态机的演进

股票系列题目引入了冷冻期和交易次数限制，状态机随之变得更加复杂。

题目：309.买卖股票的最佳时期含冷冻期

引入卖出后强制锁定 1 天的规则后，状态表示和状态转移方程如下：

• 状态表示 ：第 i i i天结束后，资产处于以下三者之一：

• d p [ i ] [ 0 ] dp[i][0] dp[i][0]（买入状态）：手中有一支股票。

• d p [ i ] [ 1 ] dp[i][1] dp[i][1]（可交易状态）：手里没股票，且今天没卖出，随时可以买。

• d p [ i ] [ 2 ] dp[i][2] dp[i][2]（冷冻期状态）：今天刚卖出股票，明天不能买。
  

• 状态转移核心：

• d p [ i ] [ 0 ] = max ⁡ ( d p [ i − 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] − p r i c e s [ i ] ) dp[i][0] = \max(dp[i-1][0], dp[i-1][1] - prices[i]) dp[i][0]=max(dp[i−1][0],dp[i−1][1]−prices[i])

• d p [ i ] [ 1 ] = max ⁡ ( d p [ i − 1 ] [ 1 ] , d p [ i − 1 ] [ 2 ] ) dp[i][1] = \max(dp[i-1][1], dp[i-1][2]) dp[i][1]=max(dp[i−1][1],dp[i−1][2])

• d p [ i ] [ 2 ] = d p [ i − 1 ] [ 0 ] + p r i c e s [ i ] dp[i][2] = dp[i-1][0] + prices[i] dp[i][2]=dp[i−1][0]+prices[i]

根据状态机得出状态转移方程

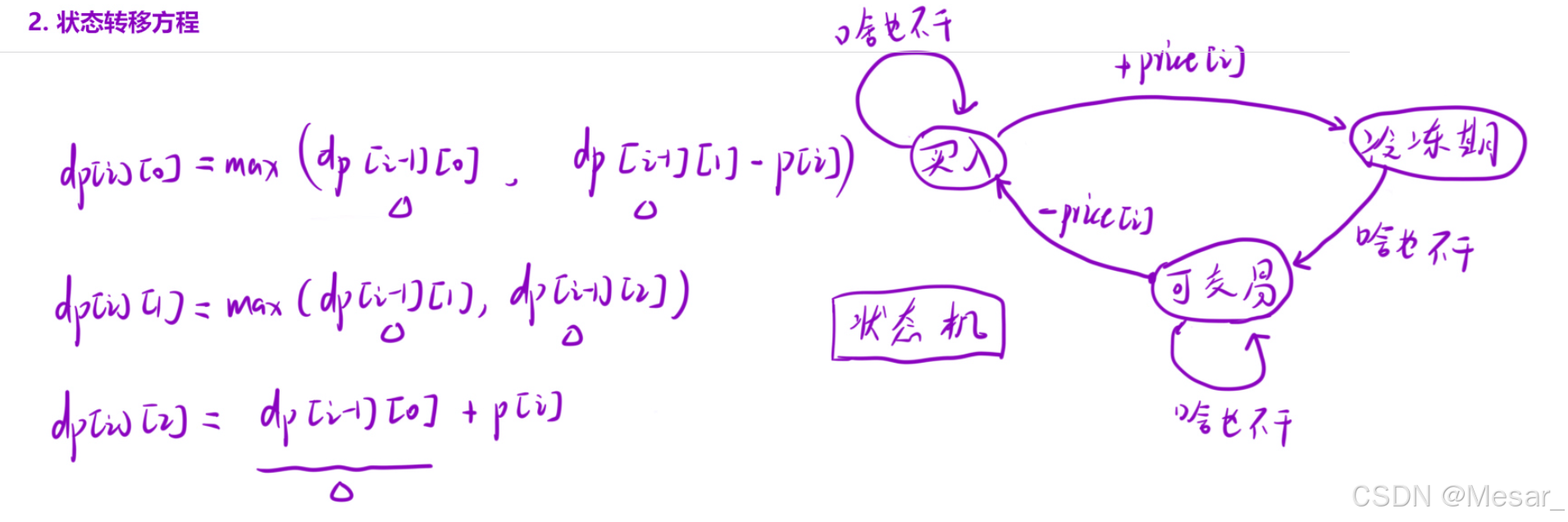
• 初始化：根据转移方程，只需要初始化0下标位置的值即可；
  

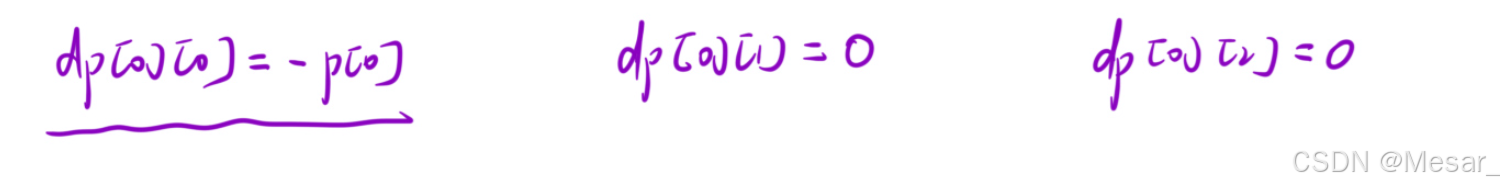
代码实现：

class Solution 
{
public:
    int maxProfit(vector<int>& prices) 
    {
        int n=prices.size();
        vector<vector<int>> dp(n,vector<int>(3,0));//0买入1可交易2冷冻期
        dp[0][0]=-prices[0];//初始化第一个位置即可（1，2都为0）

        //根据状态机转换得出状态转移方程
        for(int i=1;i<n;++i)
        {
            dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);
            dp[i][1]=max(dp[i-1][1],dp[i-1][2]);
            dp[i][2]=dp[i-1][0]+prices[i];
        }
        
        return max(dp[n-1][1],dp[n-1][2]);//最大值不会在最后一天再买入
    }
};

题目：123.买卖股票的最佳时机III

引入了"交易次数 "这一关键属性标签。

• 状态表示：
• ： f [ i ] [ j ] f[i][j] f[i][j]：第i天结束之后，完成了j次交易，此时处于"买入"状态下的最大利润
• ： g [ i ] [ j ] g[i][j] g[i][j]：第i天结束之后，完成了j次交易，此时处于"卖出"状态下的最大利润

• 状态转移的奥秘：

• 卖出触发计数 ：卖出触发计数： g [ i ] [ j ] = max ⁡ ( g [ i − 1 ] [ j ] , f [ i − 1 ] [ j − 1 ] + p r i c e s [ i ] ) g[i][j] = \max(g[i-1][j], f[i-1][j-1] + prices[i]) g[i][j]=max(g[i−1][j],f[i−1][j−1]+prices[i])。

• 逻辑解析 ：当你卖出第 j j j 支股票时，你必须从"已完成 j − 1 j-1 j−1 次交易且持股"的状态转移过来。卖出一瞬间，完成次数从 j − 1 j-1 j−1 跃升为 j j j。

• 初始化 ：为了避开非法路径（如未买入先卖出），除 g [ 0 ] [ 0 ] = 0 g[0][0]=0 g[0][0]=0 和 f [ 0 ] [ 0 ] = − p r i c e s [ 0 ] f[0][0]=-prices[0] f[0][0]=−prices[0] 外，其余均设为极小值（ I N F = 0 x 3 f 3 f 3 f INF=0x3f3f3f INF=0x3f3f3f------整形最大值的一半）这样可以避免数据溢出。

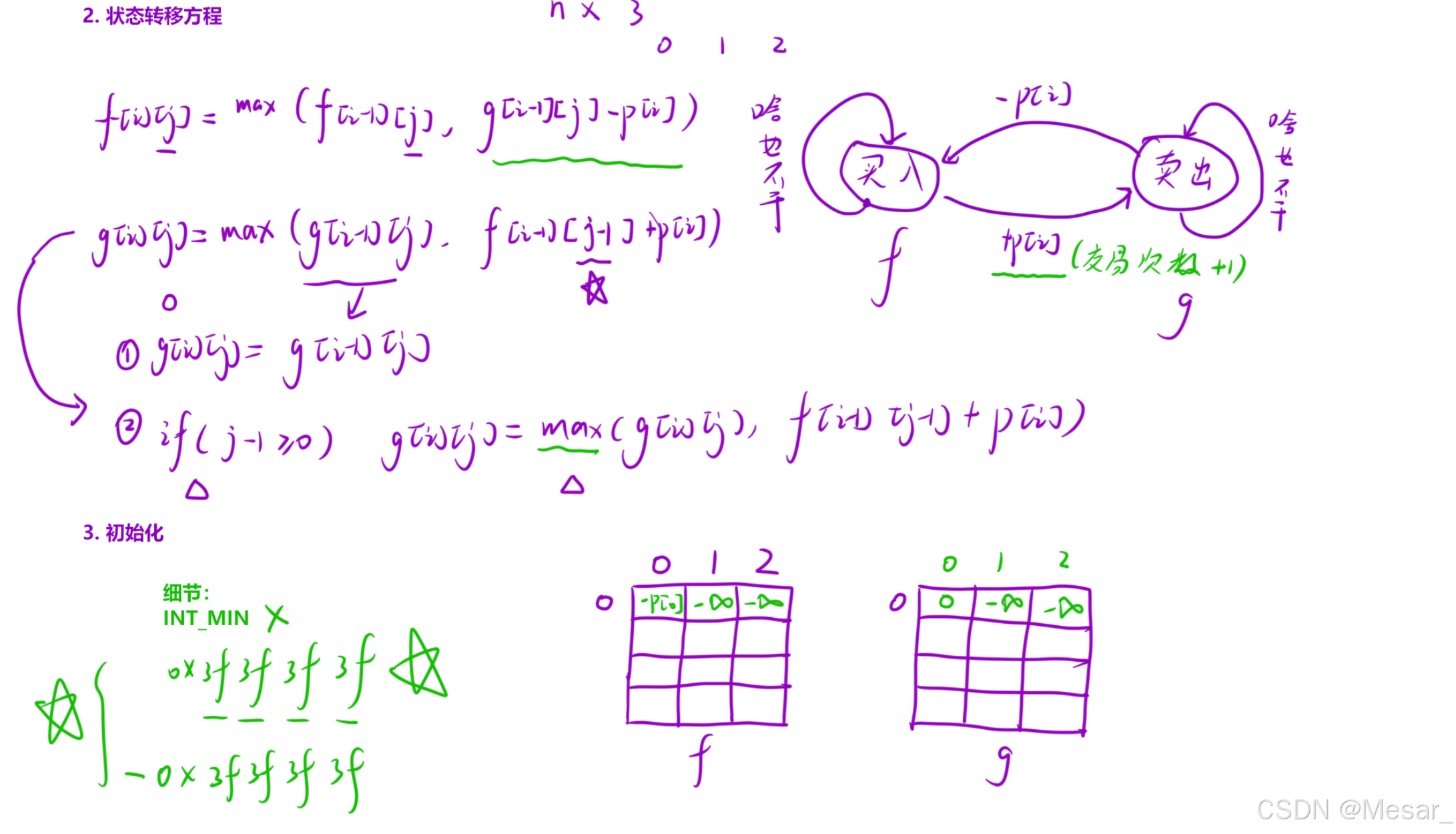
• 如何理解 j − 1 j-1 j−1

如果感到困惑是因为你在找" j = j + 1 j = j + 1 j=j+1"这样的加法语句，实际在DP表中， g [ i ] [ j ] g[i][j] g[i][j] 依赖 f [ i − 1 ] [ j − 1 ] f[i-1][j-1] f[i−1][j−1] 就等同于执行了 j = j + 1 j = j + 1 j=j+1。

• 输入： 已经完成 j − 1 j-1 j−1 次的状态。
• 动作： 卖出（触发一次交易完成）。
• 输出： 填入完成 j j j 次的状态格子里。

代码实现：

class Solution 
{
    const int INF=0x3f3f3f;//整形最大值的一半
public:
    int maxProfit(vector<int>& prices) 
    {
        int n=prices.size();
        vector<vector<int>> f(n,vector<int>(3,-INF));//避免数据溢出
        auto g=f;
        f[0][0]=-prices[0],g[0][0]=0;//初始化

        for(int i=1;i<n;++i)
        {
            for(int j=0;j<3;++j)
            {
                f[i][j]=max(f[i-1][j],g[i-1][j]-prices[i]);
                //可以通过状态方程来处理边界问题
                g[i][j]=g[i-1][j];//处理第一列
                if(j>=1)//
                {
                    g[i][j]=max(g[i-1][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        //答案在交易次数为2的那一行
        int ret=0;
        for(int i=0;i<3;++i)
        {
            ret=max(ret,g[n-1][i]);
        }
        return ret;
        
    }
};