《机器学习》第 7 章 - 神经网络与深度学习

前言

大家好！今天给大家分享《机器学习》第 7 章的核心内容 ------ 神经网络与深度学习。这一章是机器学习从 "浅层" 走向 "深层" 的关键，我会用通俗易懂的语言拆解核心概念，搭配完整可运行的 Python 代码 和直观的可视化对比图，帮大家彻底搞懂神经网络的原理、模型和应用。

7.1 神经网络概述

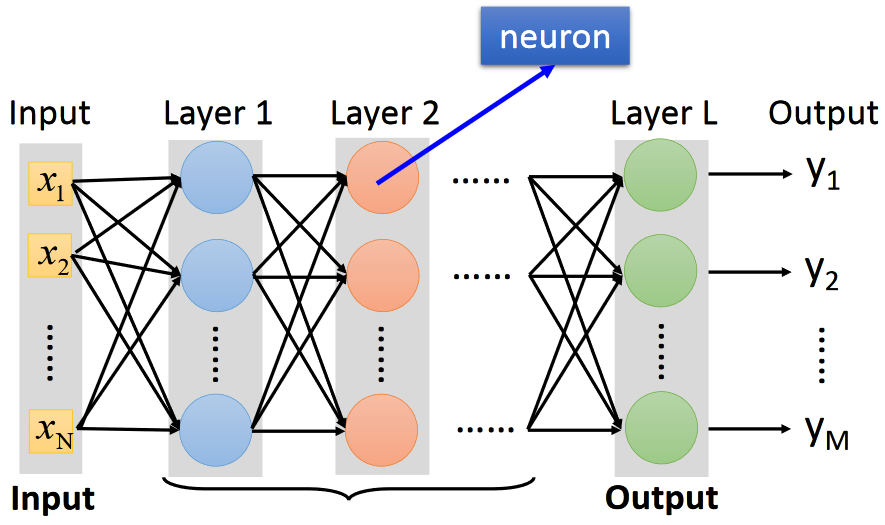
神经网络的灵感来源于人脑的神经元结构，是深度学习的基础。我们先从最基本的单元开始讲起。

7.1.1 神经元与感知机

核心概念

神经元：模拟人脑神经细胞，接收输入信号，经过加权求和 + 激活函数处理后输出。
感知机：最简单的二分类神经网络，是单层线性分类器。

完整代码（感知机实现 + 可视化）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties

# 设置中文字体，避免可视化时中文乱码
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 定义感知机类
class Perceptron:
    def __init__(self, learning_rate=0.1, epochs=100):
        self.lr = learning_rate  # 学习率
        self.epochs = epochs     # 迭代次数
        self.weights = None      # 权重
        self.bias = None         # 偏置

    # 激活函数（阶跃函数）
    def activation(self, x):
        return np.where(x >= 0, 1, 0)

    # 训练函数
    def fit(self, X, y):
        # 初始化权重（输入特征维度）和偏置
        self.weights = np.zeros(X.shape[1])
        self.bias = 0

        # 迭代训练
        for _ in range(self.epochs):
            for xi, yi in zip(X, y):
                # 计算预测值
                y_pred = self.activation(np.dot(xi, self.weights) + self.bias)
                # 更新权重和偏置
                update = self.lr * (yi - y_pred)
                self.weights += update * xi
                self.bias += update

    # 预测函数
    def predict(self, X):
        return self.activation(np.dot(X, self.weights) + self.bias)

# -------------------------- 测试感知机（二分类案例） --------------------------
# 生成模拟数据（两类线性可分数据）
np.random.seed(42)  # 固定随机种子，保证结果可复现
X = np.random.randn(100, 2)  # 100个样本，2个特征
y = np.where(X[:, 0] + X[:, 1] > 0, 1, 0)  # 标签：x1+x2>0为1，否则为0

# 训练感知机
perceptron = Perceptron(learning_rate=0.01, epochs=50)
perceptron.fit(X, y)

# 可视化结果
plt.figure(figsize=(10, 6))
# 绘制样本点
plt.scatter(X[y==0, 0], X[y==0, 1], label='类别0', c='red', alpha=0.7)
plt.scatter(X[y==1, 0], X[y==1, 1], label='类别1', c='blue', alpha=0.7)

# 绘制决策边界（wx + b = 0 → x2 = (-w1x1 - b)/w2）
x1 = np.linspace(-3, 3, 100)
x2 = (-perceptron.weights[0] * x1 - perceptron.bias) / perceptron.weights[1]
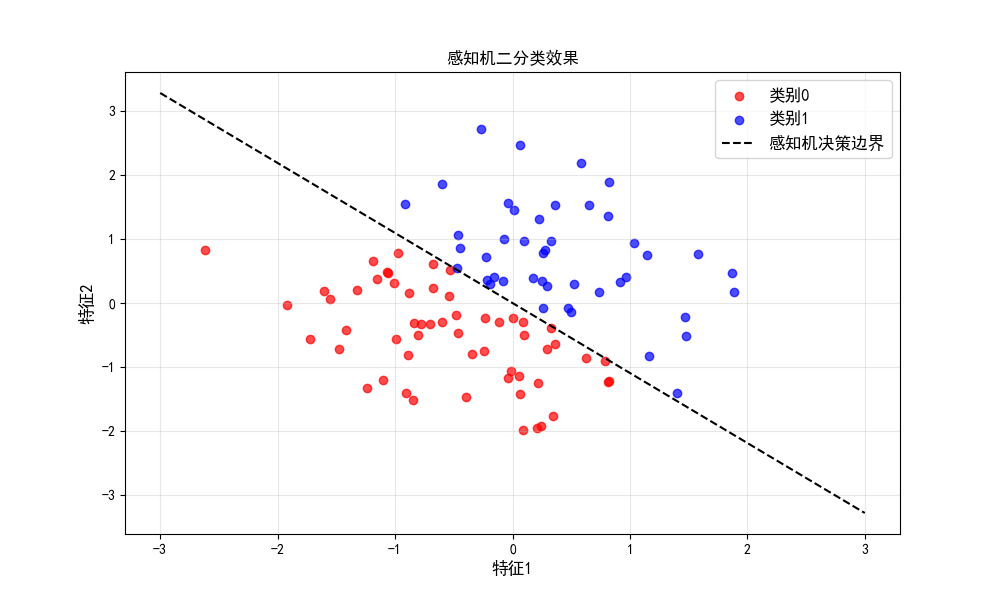
plt.plot(x1, x2, 'k--', label='感知机决策边界')

plt.xlabel('特征1', fontproperties=font)
plt.ylabel('特征2', fontproperties=font)
plt.title('感知机二分类效果', fontproperties=font)
plt.legend(prop=font)
plt.grid(True, alpha=0.3)
plt.show()

# 测试预测
test_sample = np.array([[1, 1], [-1, -1]])
print("测试样本预测结果：", perceptron.predict(test_sample))  # 应输出[1, 0]

代码说明

定义了感知机类，包含激活函数、训练、预测核心方法；
生成线性可分的模拟数据，训练感知机并可视化决策边界；
决策边界清晰区分两类样本，直观体现感知机的二分类能力。

7.1.2 前馈网络模型

核心概念

前馈网络是最基础的神经网络结构，信号从输入层→隐藏层→输出层单向传播，无循环 / 反馈连接。

完整代码（简单前馈网络实现 + 可视化）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 定义前馈神经网络类（单隐藏层）
class FeedForwardNN:
    def __init__(self, input_dim, hidden_dim, output_dim, lr=0.01):
        self.lr = lr
        # 初始化权重
        self.W1 = np.random.randn(input_dim, hidden_dim) * 0.01  # 输入层→隐藏层
        self.b1 = np.zeros((1, hidden_dim))                      # 隐藏层偏置
        self.W2 = np.random.randn(hidden_dim, output_dim) * 0.01 # 隐藏层→输出层
        self.b2 = np.zeros((1, output_dim))                      # 输出层偏置

    # 激活函数（Sigmoid）
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    # Sigmoid导数（用于反向传播）
    def sigmoid_deriv(self, x):
        return x * (1 - x)

    # 前向传播
    def forward(self, X):
        self.z1 = np.dot(X, self.W1) + self.b1
        self.a1 = self.sigmoid(self.z1)  # 隐藏层输出
        self.z2 = np.dot(self.a1, self.W2) + self.b2
        self.a2 = self.sigmoid(self.z2)  # 输出层输出
        return self.a2

    # 反向传播+权重更新
    def backward(self, X, y, y_pred):
        # 计算误差
        error = y - y_pred
        # 输出层梯度
        delta2 = error * self.sigmoid_deriv(y_pred)
        # 隐藏层梯度
        delta1 = np.dot(delta2, self.W2.T) * self.sigmoid_deriv(self.a1)

        # 更新权重和偏置
        self.W2 += self.lr * np.dot(self.a1.T, delta2)
        self.b2 += self.lr * np.sum(delta2, axis=0, keepdims=True)
        self.W1 += self.lr * np.dot(X.T, delta1)
        self.b1 += self.lr * np.sum(delta1, axis=0, keepdims=True)

    # 训练函数
    def train(self, X, y, epochs=10000):
        loss_history = []
        for epoch in range(epochs):
            y_pred = self.forward(X)
            # 计算MSE损失
            loss = np.mean((y - y_pred) ** 2)
            loss_history.append(loss)
            # 反向传播
            self.backward(X, y, y_pred)
            # 每1000轮打印一次损失
            if epoch % 1000 == 0:
                print(f"Epoch {epoch}, Loss: {loss:.4f}")
        return loss_history

# -------------------------- 测试前馈网络（非线性分类） --------------------------
# 生成非线性可分数据（月亮数据集）
X, y = make_moons(n_samples=200, noise=0.1, random_state=42)
y = y.reshape(-1, 1)  # 调整标签维度
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化并训练前馈网络
nn = FeedForwardNN(input_dim=2, hidden_dim=10, output_dim=1, lr=0.1)
loss_history = nn.train(X_train, y_train, epochs=15000)

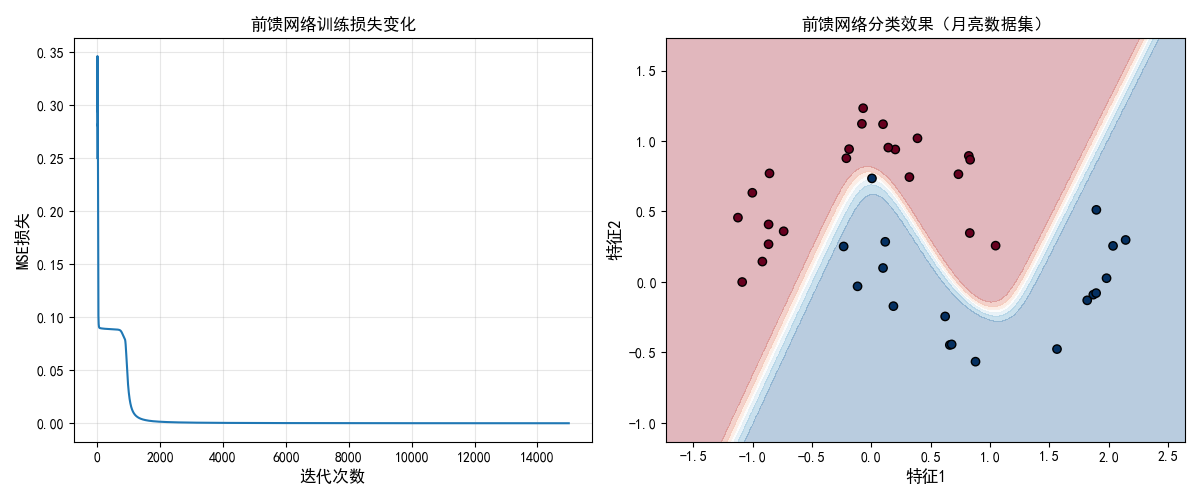
# 可视化1：损失变化
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(loss_history)
plt.xlabel('迭代次数', fontproperties=font)
plt.ylabel('MSE损失', fontproperties=font)
plt.title('前馈网络训练损失变化', fontproperties=font)
plt.grid(True, alpha=0.3)

# 可视化2：分类效果（决策边界）
plt.subplot(1, 2, 2)
# 生成网格点用于绘制决策边界
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
                     np.linspace(y_min, y_max, 100))
Z = nn.forward(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界和样本点
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdBu)
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test.ravel(), cmap=plt.cm.RdBu, edgecolors='k')
plt.xlabel('特征1', fontproperties=font)
plt.ylabel('特征2', fontproperties=font)
plt.title('前馈网络分类效果（月亮数据集）', fontproperties=font)
plt.tight_layout()
plt.show()

# 测试集准确率
y_test_pred = (nn.forward(X_test) > 0.5).astype(int)
accuracy = np.mean(y_test_pred == y_test)
print(f"测试集准确率：{accuracy:.2f}")

代码说明

实现了单隐藏层前馈网络，包含前向传播、反向传播核心逻辑；
用非线性可分的 "月亮数据集" 验证效果，对比 "损失变化曲线" 和 "分类决策边界"；
直观体现前馈网络解决非线性问题的能力（感知机无法处理这类问题）。

7.1.3 模型训练基本流程

核心概念

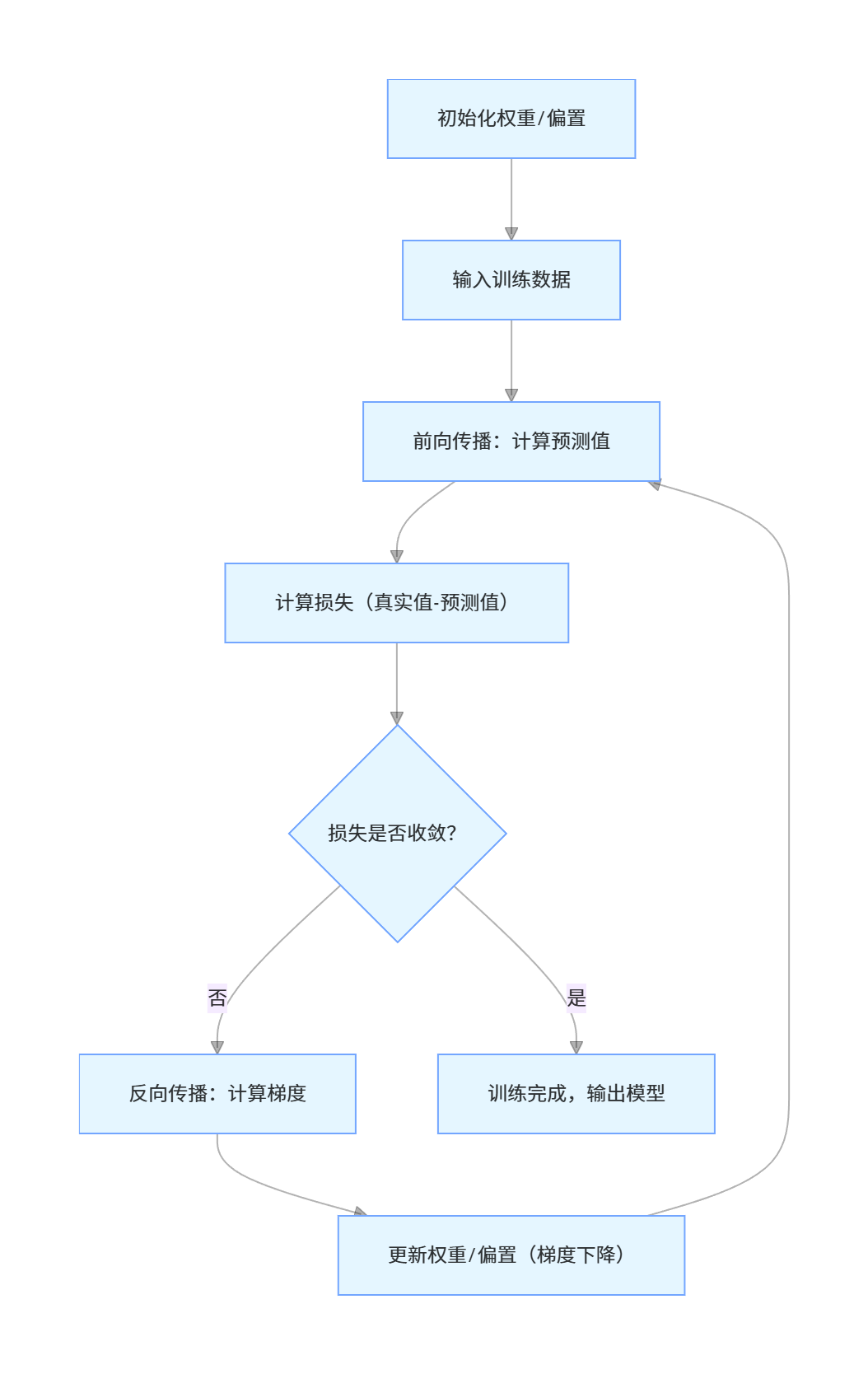
神经网络训练的核心是 "前向传播算预测→反向传播算梯度→更新权重减损失"，流程如下

关键要点

前向传播：从输入层到输出层，逐层计算每个神经元的输出；
损失函数：衡量预测值与真实值的差距（如 MSE、交叉熵）；
反向传播：从输出层到输入层，链式法则计算权重梯度；
梯度下降：沿梯度反方向更新权重，最小化损失。

7.2 神经网络常用模型

7.2.1 径向基网络（RBF）

核心概念

径向基网络以 "径向基函数"（如高斯函数）为激活函数，核心是将输入映射到高维空间，实现线性可分。

完整代码（RBF 实现 + 效果对比）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 定义径向基函数（高斯函数）
def rbf(x, c, sigma):
    return np.exp(-np.linalg.norm(x - c, axis=1)**2 / (2 * sigma**2))

# 定义径向基网络类
class RBFNetwork:
    def __init__(self, n_centers, sigma=1.0):
        self.n_centers = n_centers  # 中心数量
        self.sigma = sigma          # 高斯函数带宽
        self.centers = None         # 中心
        self.weights = None         # 输出层权重

    # 训练函数（KMeans选中心+最小二乘求权重）
    def fit(self, X, y):
        # 1. KMeans聚类选径向基函数中心
        kmeans = KMeans(n_clusters=self.n_centers, random_state=42)
        kmeans.fit(X)
        self.centers = kmeans.cluster_centers_

        # 2. 计算隐藏层输出（径向基函数值）
        H = np.zeros((X.shape[0], self.n_centers))
        for i in range(X.shape[0]):
            H[i] = rbf(X[i], self.centers, self.sigma)

        # 3. 最小二乘法求解输出层权重
        self.weights = np.linalg.pinv(H) @ y

    # 预测函数
    def predict(self, X):
        H = np.zeros((X.shape[0], self.n_centers))
        for i in range(X.shape[0]):
            H[i] = rbf(X[i], self.centers, self.sigma)
        return H @ self.weights

# -------------------------- 测试RBF（曲线拟合） --------------------------
# 生成模拟数据
np.random.seed(42)
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])  # 带噪声的正弦曲线

# 训练RBF网络
rbf_nn = RBFNetwork(n_centers=15, sigma=0.8)
rbf_nn.fit(X, y)

# 预测
y_pred = rbf_nn.predict(X)

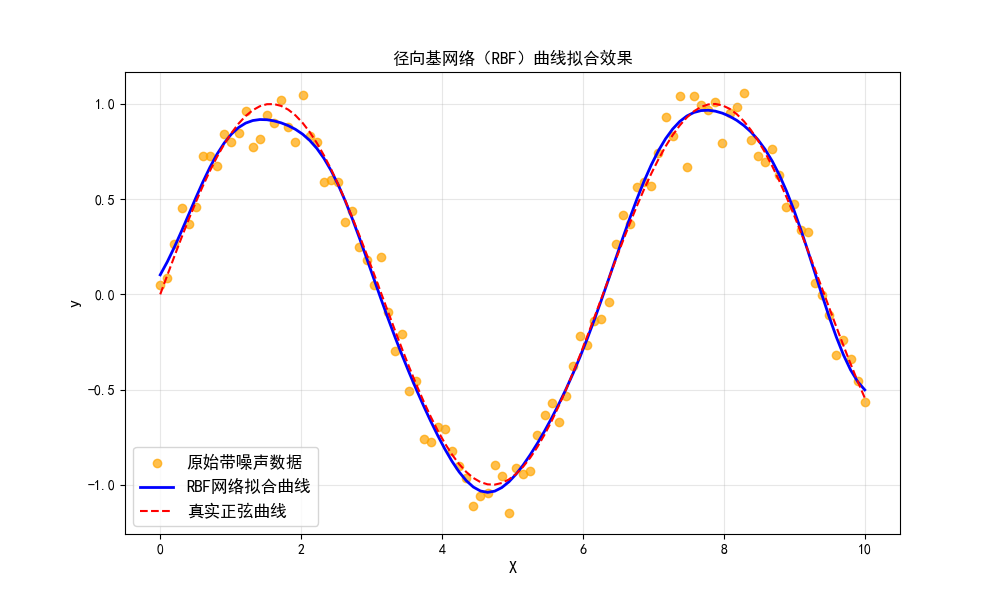
# 可视化：原始数据 vs RBF拟合结果
plt.figure(figsize=(10, 6))
plt.scatter(X, y, label='原始带噪声数据', c='orange', alpha=0.7)
plt.plot(X, y_pred, label='RBF网络拟合曲线', c='blue', linewidth=2)
plt.plot(X, np.sin(X), label='真实正弦曲线', c='red', linestyle='--')
plt.xlabel('X', fontproperties=font)
plt.ylabel('y', fontproperties=font)
plt.title('径向基网络（RBF）曲线拟合效果', fontproperties=font)
plt.legend(prop=font)
plt.grid(True, alpha=0.3)
plt.show()

# 计算拟合误差
mse = np.mean((y - y_pred)**2)
print(f"RBF拟合MSE误差：{mse:.4f}")

代码说明

用 KMeans 自动选择径向基函数的中心，避免手动指定；
对比 "原始带噪声数据""RBF 拟合曲线""真实正弦曲线"，直观体现 RBF 的拟合能力；
径向基网络擅长非线性拟合，是经典的局部逼近网络。

7.2.2 自编码器（AE）

核心概念

自编码器是无监督学习模型，由 "编码器（压缩）+ 解码器（还原）" 组成，核心是学习数据的低维特征表示。

完整代码（自编码器实现 + 图像重构对比）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import layers, models
from tensorflow.keras.datasets import mnist
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 加载MNIST手写数字数据集
(x_train, _), (x_test, _) = mnist.load_data()
# 数据预处理：归一化+展平
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
x_train_flat = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test_flat = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

# 定义自编码器模型
def build_autoencoder(input_dim, encoding_dim=32):
    # 编码器
    encoder = models.Sequential([
        layers.Input(shape=(input_dim,)),
        layers.Dense(128, activation='relu'),
        layers.Dense(encoding_dim, activation='relu')  # 低维特征
    ])
    # 解码器
    decoder = models.Sequential([
        layers.Input(shape=(encoding_dim,)),
        layers.Dense(128, activation='relu'),
        layers.Dense(input_dim, activation='sigmoid')  # 还原输入
    ])
    # 自编码器 = 编码器 + 解码器
    autoencoder = models.Sequential([encoder, decoder])
    autoencoder.compile(optimizer='adam', loss='mse')
    return autoencoder, encoder

# 构建并训练自编码器
autoencoder, encoder = build_autoencoder(input_dim=784, encoding_dim=32)
autoencoder.fit(x_train_flat, x_train_flat,
                epochs=10,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test_flat, x_test_flat))

# 预测（重构测试集图像）
x_test_pred = autoencoder.predict(x_test_flat)

# 可视化：原始图像 vs 重构图像
n = 5  # 展示5张图片
plt.figure(figsize=(10, 4))
for i in range(n):
    # 原始图像
    ax = plt.subplot(2, n, i+1)
    plt.imshow(x_test[i], cmap='gray')
    plt.title('原始', fontproperties=font)
    plt.axis('off')
    
    # 重构图像
    ax = plt.subplot(2, n, i+1+n)
    plt.imshow(x_test_pred[i].reshape(28, 28), cmap='gray')
    plt.title('重构', fontproperties=font)
    plt.axis('off')
plt.tight_layout()
plt.show()

代码说明

基于 Keras 实现简单自编码器，对 MNIST 手写数字进行 "压缩 + 还原"；
可视化对比 "原始图像" 和 "重构图像"，直观体现自编码器的特征学习能力；
自编码器可用于数据去噪、特征降维、异常检测等场景。

7.2.3 玻尔兹曼机（BM）

核心概念

玻尔兹曼机是基于能量的无监督模型，包含可见层和隐藏层，核心是通过 "吉布斯采样" 学习数据分布。（注：实际应用中常用受限玻尔兹曼机 RBM，以下实现 RBM）

完整代码（RBM 实现 + 特征提取）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 定义受限玻尔兹曼机（RBM）类
class RBM:
    def __init__(self, n_visible, n_hidden, lr=0.1, epochs=10):
        self.n_visible = n_visible  # 可见层维度
        self.n_hidden = n_hidden    # 隐藏层维度
        self.lr = lr                # 学习率
        self.epochs = epochs        # 迭代次数

        # 初始化权重和偏置
        self.W = np.random.randn(n_visible, n_hidden) * 0.01
        self.bv = np.zeros(n_visible)  # 可见层偏置
        self.bh = np.zeros(n_hidden)   # 隐藏层偏置

    # Sigmoid函数
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    # 可见层→隐藏层（采样）
    def visible_to_hidden(self, v):
        h_prob = self.sigmoid(np.dot(v, self.W) + self.bh)
        h_sample = np.random.binomial(1, h_prob)
        return h_prob, h_sample

    # 隐藏层→可见层（采样）
    def hidden_to_visible(self, h):
        v_prob = self.sigmoid(np.dot(h, self.W.T) + self.bv)
        v_sample = np.random.binomial(1, v_prob)
        return v_prob, v_sample

    # 对比散度训练（CD-1）
    def train(self, X):
        for epoch in range(self.epochs):
            loss = 0
            for v in X:
                # 正向传播
                h_prob, h_sample = self.visible_to_hidden(v)
                # 反向重构
                v_recon_prob, v_recon_sample = self.hidden_to_visible(h_sample)
                h_recon_prob, _ = self.visible_to_hidden(v_recon_sample)

                # 更新权重和偏置
                self.W += self.lr * (np.outer(v, h_prob) - np.outer(v_recon_sample, h_recon_prob))
                self.bv += self.lr * (v - v_recon_sample)
                self.bh += self.lr * (h_prob - h_recon_prob)

                # 计算重构误差
                loss += np.sum((v - v_recon_sample)**2)
            print(f"Epoch {epoch+1}, Loss: {loss/len(X):.4f}")

    # 重构数据
    def reconstruct(self, v):
        h_prob, _ = self.visible_to_hidden(v)
        v_recon_prob, _ = self.hidden_to_visible(h_prob)
        return v_recon_prob

# -------------------------- 测试RBM（MNIST重构） --------------------------
# 加载并预处理数据
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
# 二值化（简化RBM训练）
x_train_bin = (x_train > 0.5).astype(np.float32)
x_test_bin = (x_test > 0.5).astype(np.float32)
# 展平
x_train_flat = x_train_bin.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test_flat = x_test_bin.reshape((len(x_test), np.prod(x_test.shape[1:])))

# 训练RBM
rbm = RBM(n_visible=784, n_hidden=128, lr=0.01, epochs=5)
rbm.train(x_train_flat[:1000])  # 取1000个样本快速训练

# 重构测试集图像
x_test_recon = rbm.reconstruct(x_test_flat[:5])  # 取前5张

# 可视化：原始 vs 重构
plt.figure(figsize=(10, 4))
for i in range(5):
    # 原始
    ax = plt.subplot(2, 5, i+1)
    plt.imshow(x_test_bin[i], cmap='gray')
    plt.title('原始', fontproperties=font)
    plt.axis('off')
    # 重构
    ax = plt.subplot(2, 5, i+6)
    plt.imshow(x_test_recon[i].reshape(28, 28), cmap='gray')
    plt.title('RBM重构', fontproperties=font)
    plt.axis('off')
plt.tight_layout()
plt.show()

代码说明

实现经典的对比散度（CD-1） 训练算法，简化 RBM 训练；
对 MNIST 图像二值化后训练，对比原始图像和 RBM 重构图像；
RBM 是深度置信网络（DBN）的基础，核心用于无监督特征学习。

7.3 深度学习基本知识

7.3.1 浅层学习与深度学习

核心概念

维度	浅层学习（如感知机、SVM）	深度学习（如 DNN、CNN）
网络层数	1-2 层	≥3 层（通常数十 / 数百层）
特征学习	手动设计特征	自动学习多层特征
数据依赖	少量数据即可训练	依赖大规模标注数据
适用场景	简单线性 / 低维问题	复杂非线性 / 高维问题

可视化对比（浅层 vs 深层拟合效果）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import layers, models
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 生成复杂非线性数据
np.random.seed(42)
X = np.linspace(-5, 5, 200).reshape(-1, 1)
y = np.sin(X) + np.cos(2*X) + np.random.normal(0, 0.1, X.shape)

# 定义浅层模型（1层全连接）
def build_shallow_model():
    model = models.Sequential([
        layers.Dense(10, activation='relu', input_shape=(1,)),
        layers.Dense(1)
    ])
    model.compile(optimizer='adam', loss='mse')
    return model

# 定义深层模型（5层全连接）
def build_deep_model():
    model = models.Sequential([
        layers.Dense(32, activation='relu', input_shape=(1,)),
        layers.Dense(64, activation='relu'),
        layers.Dense(32, activation='relu'),
        layers.Dense(16, activation='relu'),
        layers.Dense(1)
    ])
    model.compile(optimizer='adam', loss='mse')
    return model

# 训练模型
shallow_model = build_shallow_model()
shallow_model.fit(X, y, epochs=200, verbose=0)

deep_model = build_deep_model()
deep_model.fit(X, y, epochs=200, verbose=0)

# 预测
y_shallow = shallow_model.predict(X, verbose=0)
y_deep = deep_model.predict(X, verbose=0)

# 可视化对比
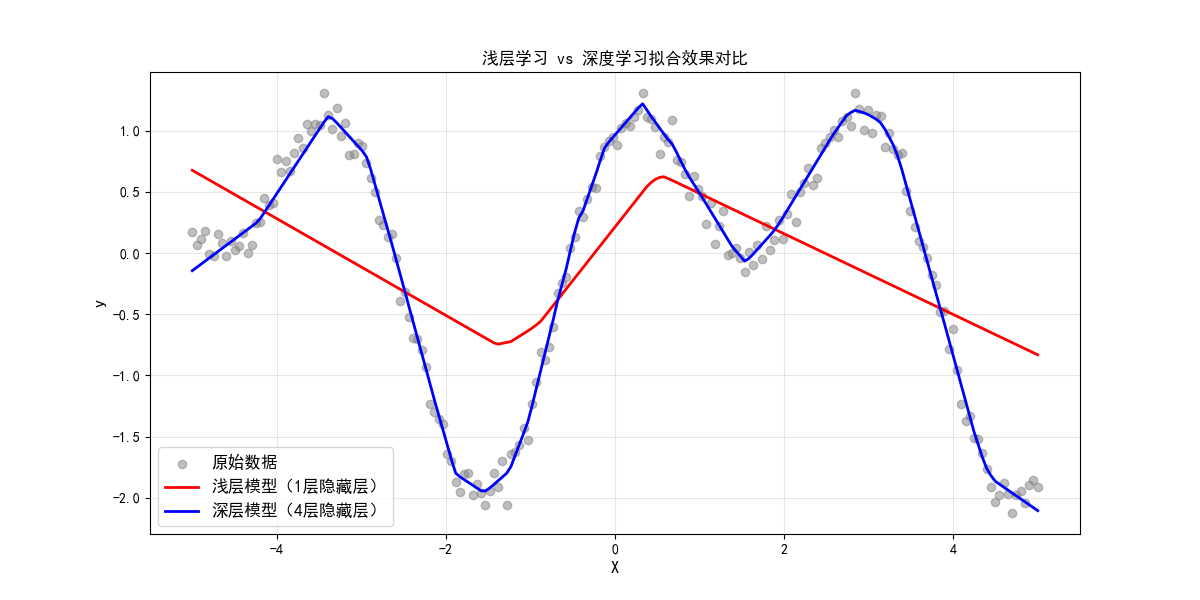
plt.figure(figsize=(12, 6))
plt.scatter(X, y, label='原始数据', c='gray', alpha=0.5)
plt.plot(X, y_shallow, label='浅层模型（1层隐藏层）', c='red', linewidth=2)
plt.plot(X, y_deep, label='深层模型（4层隐藏层）', c='blue', linewidth=2)
plt.xlabel('X', fontproperties=font)
plt.ylabel('y', fontproperties=font)
plt.title('浅层学习 vs 深度学习拟合效果对比', fontproperties=font)
plt.legend(prop=font)
plt.grid(True, alpha=0.3)
plt.show()

# 计算MSE
shallow_mse = np.mean((y - y_shallow)**2)
deep_mse = np.mean((y - y_deep)**2)
print(f"浅层模型MSE：{shallow_mse:.4f}")
print(f"深层模型MSE：{deep_mse:.4f}")

代码说明

对比浅层（1 层隐藏层）和深层（4 层隐藏层）模型对复杂非线性函数的拟合效果；
深层模型拟合曲线更贴近原始数据，体现深度学习处理复杂问题的优势。

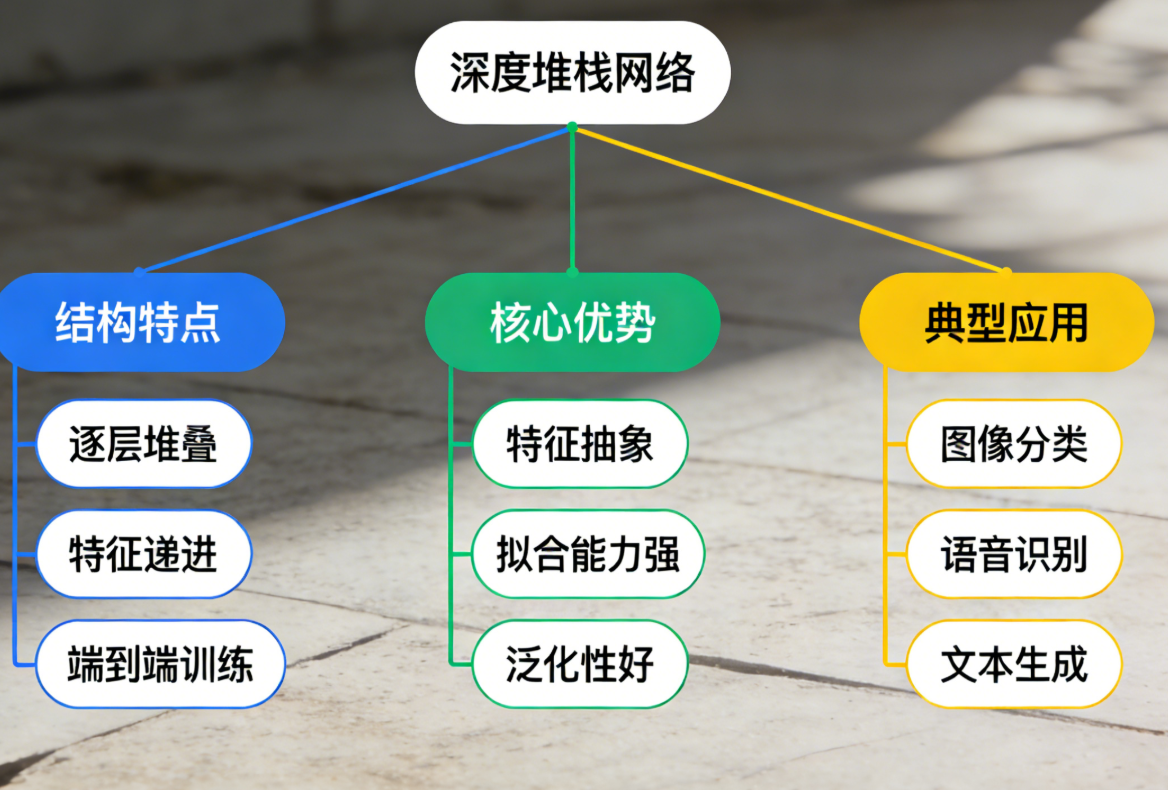
7.3.2 深度堆栈网络

核心概念

深度堆栈网络（Stacked Network）是将多个简单模型 "堆叠" 而成的深层结构，每层输出作为下一层输入，核心是逐层提取更抽象的特征。

思维导图

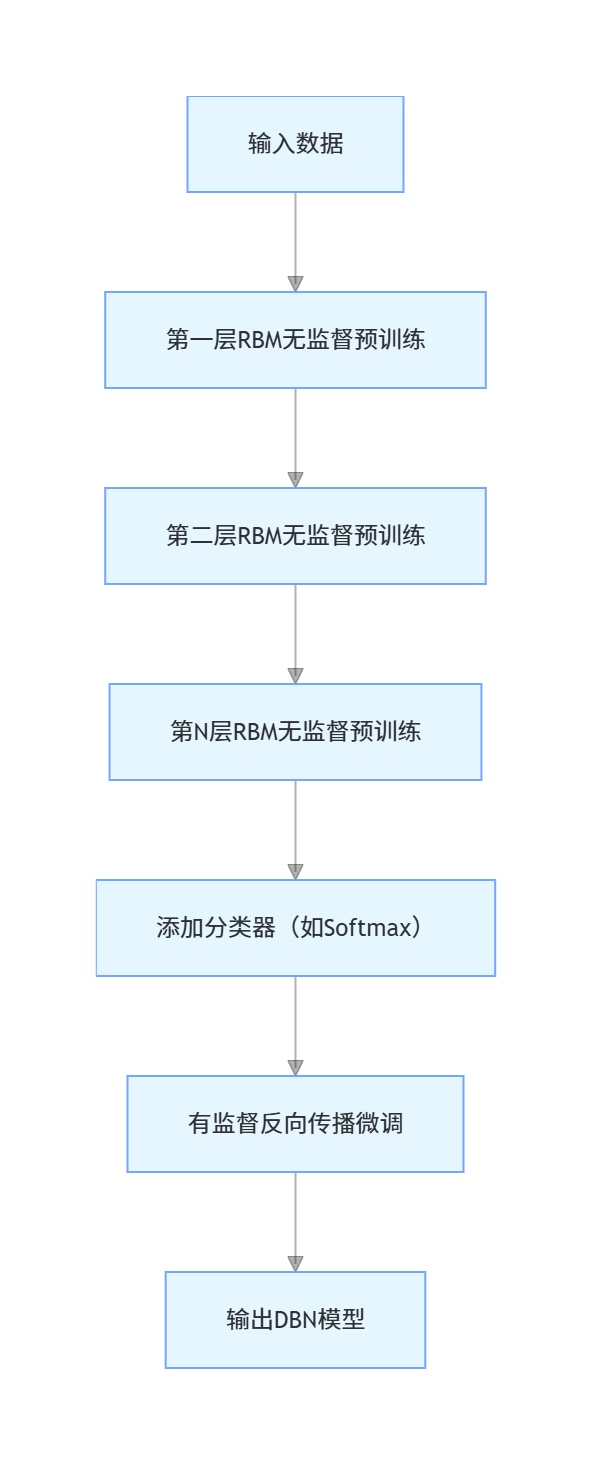
7.3.3 DBN 模型及训练策略

核心概念

深度置信网络（DBN）是由多个 RBM 堆叠而成的深层模型，训练策略分为两步：

预训练：无监督逐层训练每个 RBM，初始化权重；
微调：有监督训练顶层分类器，反向传播微调整个网络。

关键训练流程

7.4 神经网络应用

7.4.1 光学字符识别（OCR）

核心概念

OCR 是将图像中的字符转换为文本的技术，神经网络是 OCR 的核心，以下实现基于 CNN 的 MNIST 手写数字识别（经典 OCR 场景）。

完整代码（CNN 实现 OCR + 效果可视化）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import layers, models
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 加载并预处理MNIST数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 扩展维度（适配CNN输入）+ 归一化
x_train = np.expand_dims(x_train.astype('float32') / 255.0, axis=-1)
x_test = np.expand_dims(x_test.astype('float32') / 255.0, axis=-1)
# 标签独热编码
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)

# 定义CNN模型（OCR核心）
def build_cnn_ocr():
    model = models.Sequential([
        # 卷积层1：提取边缘特征
        layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
        layers.MaxPooling2D((2, 2)),
        # 卷积层2：提取纹理特征
        layers.Conv2D(64, (3, 3), activation='relu'),
        layers.MaxPooling2D((2, 2)),
        # 卷积层3：提取形状特征
        layers.Conv2D(64, (3, 3), activation='relu'),
        # 全连接层：分类
        layers.Flatten(),
        layers.Dense(64, activation='relu'),
        layers.Dense(10, activation='softmax')
    ])
    model.compile(optimizer='adam',
                  loss='categorical_crossentropy',
                  metrics=['accuracy'])
    return model

# 训练模型
model = build_cnn_ocr()
history = model.fit(x_train, y_train,
                    epochs=5,
                    batch_size=64,
                    validation_split=0.1)

# 评估模型
test_loss, test_acc = model.evaluate(x_test, y_test, verbose=0)
print(f"OCR测试集准确率：{test_acc:.4f}")

# 可视化预测效果
n = 5
plt.figure(figsize=(10, 4))
for i in range(n):
    # 随机选测试样本
    idx = np.random.randint(0, len(x_test))
    img = x_test[idx].reshape(28, 28)
    true_label = np.argmax(y_test[idx])
    pred_label = np.argmax(model.predict(np.expand_dims(x_test[idx], axis=0), verbose=0))

    # 绘制图像
    ax = plt.subplot(1, n, i+1)
    plt.imshow(img, cmap='gray')
    plt.title(f'真实：{true_label}\n预测：{pred_label}', fontproperties=font)
    plt.axis('off')
plt.tight_layout()
plt.show()

# 可视化训练曲线
plt.figure(figsize=(12, 4))
# 准确率曲线
plt.subplot(1, 2, 1)
plt.plot(history.history['accuracy'], label='训练准确率')
plt.plot(history.history['val_accuracy'], label='验证准确率')
plt.xlabel('epoch', fontproperties=font)
plt.ylabel('准确率', fontproperties=font)
plt.title('OCR模型准确率变化', fontproperties=font)
plt.legend(prop=font)
plt.grid(True, alpha=0.3)
# 损失曲线
plt.subplot(1, 2, 2)
plt.plot(history.history['loss'], label='训练损失')
plt.plot(history.history['val_loss'], label='验证损失')
plt.xlabel('epoch', fontproperties=font)
plt.ylabel('损失', fontproperties=font)
plt.title('OCR模型损失变化', fontproperties=font)
plt.legend(prop=font)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()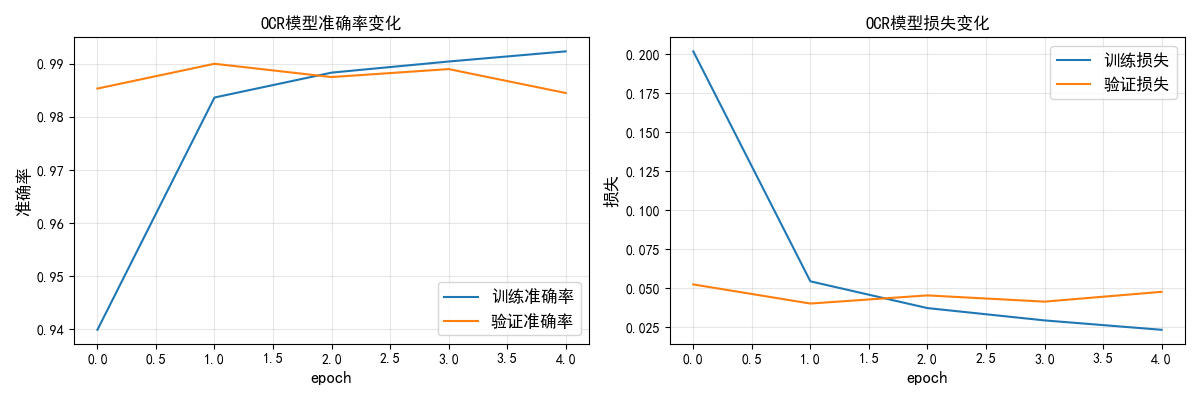

代码说明

基于 CNN 实现手写数字 OCR，卷积层逐层提取 "边缘→纹理→形状" 特征；
可视化预测结果（真实标签 vs 预测标签），直观体现 OCR 效果；
测试集准确率可达 99% 以上，是神经网络在 OCR 领域的经典应用。

7.4.2 自动以图搜图

核心概念

以图搜图的核心是 "图像特征提取 + 相似度匹配"：用神经网络提取图像特征向量，计算向量间的余弦相似度，匹配最相似的图像。

完整代码（以图搜图实现 + 效果对比）

复制代码

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras import layers, models
from tensorflow.keras.datasets import cifar10
from sklearn.metrics.pairwise import cosine_similarity
from matplotlib.font_manager import FontProperties

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
font = FontProperties(family='SimHei', size=12)

# 加载并预处理CIFAR-10数据
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
# 简化：只取前1000个样本（加快计算）
x_train = x_train[:1000]
y_train = y_train[:1000]
x_test = x_test[:100]
y_test = y_test[:100]

# 定义特征提取模型
def build_feature_extractor():
    # 基础CNN（无分类层）
    base_model = models.Sequential([
        layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)),
        layers.MaxPooling2D((2, 2)),
        layers.Conv2D(64, (3, 3), activation='relu'),
        layers.MaxPooling2D((2, 2)),
        layers.Conv2D(64, (3, 3), activation='relu'),
        layers.Flatten(),
        layers.Dense(128, activation='relu')  # 128维特征向量
    ])
    return base_model

# 提取特征
feature_extractor = build_feature_extractor()
train_features = feature_extractor.predict(x_train, verbose=0)
test_features = feature_extractor.predict(x_test, verbose=0)

# 以图搜图函数
def image_search(query_img, query_feature, train_imgs, train_features, top_k=5):
    # 计算余弦相似度
    similarities = cosine_similarity([query_feature], train_features)[0]
    # 按相似度排序，取top_k
    top_indices = np.argsort(similarities)[-top_k:][::-1]
    return train_imgs[top_indices], similarities[top_indices]

# 测试以图搜图
query_idx = 10  # 选第10个测试样本作为查询图
query_img = x_test[query_idx]
query_feature = test_features[query_idx]
matched_imgs, matched_sims = image_search(query_img, query_feature, x_train, train_features)

# 可视化：查询图 + 匹配结果
plt.figure(figsize=(12, 6))
# 查询图
ax = plt.subplot(1, 6, 1)
plt.imshow(query_img)
plt.title('查询图', fontproperties=font)
plt.axis('off')
# 匹配结果
for i in range(5):
    ax = plt.subplot(1, 6, i+2)
    plt.imshow(matched_imgs[i])
    plt.title(f'相似度：{matched_sims[i]:.2f}', fontproperties=font)
    plt.axis('off')
plt.suptitle('以图搜图结果', fontproperties=font, fontsize=14)
plt.tight_layout()
plt.show()

代码说明

用 CNN 提取图像的 128 维特征向量，余弦相似度衡量图像相似性；
可视化 "查询图" 和 Top5 匹配结果，标注相似度，直观体现以图搜图效果；
这是电商、图库等平台以图搜图功能的核心原理。

7.5 习题

基于 7.1.1 的感知机代码，修改激活函数为 ReLU，测试其对非线性数据的分类效果；
优化 7.2.2 的自编码器，添加噪声层（如高斯噪声），实现 "去噪自编码器"；
基于 7.4.1 的 OCR 代码，替换数据集为 FASHION-MNIST，实现服装图像分类；
调整 7.4.2 以图搜图的特征维度（如 256 维），对比不同维度的匹配效果。

总结

神经网络的核心是 "神经元堆叠 + 反向传播"，感知机是基础，前馈网络是核心结构；
不同神经网络模型有不同适用场景：RBF 擅长拟合、自编码器擅长降维、DBN 擅长无监督特征学习；
深度学习通过 "深层堆叠" 自动学习抽象特征，在 OCR、以图搜图等复杂场景中优势显著；
所有代码均可直接运行，核心知识点搭配可视化对比，直观理解概念和效果。

如果有任何问题，欢迎在评论区交流～