【力扣LeetCode热题h100】哈希、双指针、滑动窗口

力扣LeetCode热题h100------哈希、双指针、滑动窗口

• 哈希
• • [1. 两数之和](#1. 两数之和)
  • [2. 字母异位词分组](#2. 字母异位词分组)
  • [3. 最长连续序列](#3. 最长连续序列)
• 双指针
• • [4. 移动零](#4. 移动零)
  • [5. 盛最多水的容器](#5. 盛最多水的容器)
  • [6. 三数之和](#6. 三数之和)
  • [7. 接雨水](#7. 接雨水)
• 滑动窗口
• • [8. 无重复的最长子串](#8. 无重复的最长子串)
  • [9. 找到字符串中所有字母异位词](#9. 找到字符串中所有字母异位词)

哈希

1. 两数之和

题目：

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数, 并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

代码1： 暴力

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        
        for(int i=0; i<n; i++){
            for(int j=i+1; j<n; j++){
                 if(nums[i]+nums[j] == target)
                    return {i, j};
            }
        }
        return {};
    }
};

分析：

暴力解法，固定一个，另一个滑动搜索，复杂度为 O ( n 2 ) \quad O(n^2) O(n2)

代码2： 先排序再双指针查找：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();

        // 存成num和idx的pair，排序的时候按照num排，
        vector<pair<int, int>> num_idx;
        for (int i = 0; i < n; i++)
            num_idx.push_back({nums[i], i});

        sort(num_idx.begin(), num_idx.end());

        // 常规的双指针前后查找
        int  left=0, right=n-1;
        while(left < right){
            int sum = num_idx[left].first + num_idx[right].first;
            if(sum == target)
                return {num_idx[left].second, num_idx[right].second};
            else if(sum > target)
                right--;
            else
                left++;
        }
        return {};
    }
};

分析：

题目给的nums数组是无序的，可以先快排，再双指针找，快排的时间复杂度为 O ( n log ⁡ n ) \quad O(n \log n) O(nlogn)，双指针前后向中间靠近的复杂度为 O ( n ) \quad O(n) O(n),所以时间复杂度为复杂度为 O ( n log ⁡ n ) \quad O(n \log n) O(nlogn)
代码3： 哈希表：

class Solution {
    public int[] twoSum(int[] nums, int target) {
        // 两数之和 梦的开始~
        Map<Integer, Integer> dict = new HashMap<>();

        for(int i = 0; ; i++){
            int x = nums[i];
            if(dict.containsKey(target - x)){
                return new int[] {i, dict.get(target - x)};
            }
            dict.put(x, i);
        }
    }
}

总结：

• 第一次用纯c++做题，背住nums.size()而不是nums.length()
• 记住vector<pair<int, int>> num_idx再num_idx.push_back({nums[i], i})的这种pair存idx的技巧，sort的时候用的是begin和end
• 最后一定要返回一下，之前c做题的时候都是返回0
• 二刷感悟 人生苦短 我用java6

---

2. 字母异位词分组

题目：

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

代码：用key-value对

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string, vector<string>> mp;
        for(string str: strs){
            string key = str;
            // c++竟然可以直接对字符排序！！
            sort(key.begin(), key.end());
            // 把key相同的value放在一起
            mp[key].emplace_back(str);
        }

        vector<vector<string>> ans;
        for(auto it=mp.begin(); it!=mp.end(); it++)
            //每次取出来的是key-value的pair，所以放的是second   
            ans.emplace_back(it->second);
        
        return ans;
    }
};

class Solution { // java 代码
    public List<List<String>> groupAnagrams(String[] strs) {
        // Key: 排序后的字符串 (例如 "aet")
        // Value: 原字符串列表 (例如 ["eat", "tea", "ate"])
        Map<String, List<String>> map = new HashMap<>();

        for (String s : strs) {
            // 1. 把字符串转化成字符数组
            char[] ch = s.toCharArray();
            // 2. 排序 (这就是生成 Key 的过程)
            Arrays.sort(ch);
            // 3. 变回字符串作为 Key
            String key = new String(ch);

            // 4. 放入 Map
            // computeIfAbsent 是 Java 8 的写法，等价于：
            // if (!map.containsKey(key)) map.put(key, new ArrayList<>());
            // map.get(key).add(s);
            map.computeIfAbsent(key, k -> new ArrayList<>()).add(s);
        }

        // 5. 返回 Map 中所有的 Values
        return new ArrayList<>(map.values());
    }
}

分析：

• 字母异位词满足set(str1) == set(str2),当然这个set是不包含去重功能的,即把一个单词看成一个集合的话，两个集合是相等的，所以["nat","tan"],["ate","eat","tea"]他们之间分别是字母异位词，所以可以将每个字母分别排序作为map的key，key相同的就是一组异位词，如上代码定义unordered_map<string, vector<string>> mp;,map的key是一个string，第二项是string的vector
• 复杂度为 O ( n k log ⁡ k ) \quad O(nk \log k) O(nklogk), n n n为单词个数， k k k为单词的最大长度 ， O ( k log ⁡ k ) \quad O(k \log k) O(klogk)是对单词排序的复杂度

总结：

• 记住unordered_map<string, vector<string>> mp;这种定义map的方式，直接mp[key].emplace_back(str);就可以存
• 对于ans.emplace_back(it->second);每次取出来的是key-value的pair，所以放的是second

---

3. 最长连续序列

40min
题目：

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O ( n ) O(n) O(n) 的算法解决此问题。

代码1：先排序，再逐个判断

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        if(nums.size() == 0) return 0;
        sort(nums.begin(), nums.end());

        int ans = 0;
        int count = 0;
        for(int i=1; i<nums.size(); i++){
            if(nums[i] == nums[i-1]+1)
                count++;
            else if(nums[i] == nums[i-1])
                continue;
            else{
                ans = max(count, ans);
                count = 0;
            }
        }
        return max(++count, ++ans);
    }
};

分析：

• 按照常人思考的逻辑从小到大一个个往后找，找的过程中满足+1和去重的条件，时间复杂度为：排序+找 = O ( n log ⁡ n ) + O ( n ) = O ( n log ⁡ n ) \quad O(n \log n)+\quad O(n) =\quad O(n \log n) O(nlogn)+O(n)=O(nlogn)

代码2：分析最长子序列的性质

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> num_set;
        for(int num: nums) //集合去重
            num_set.insert(num);

        int ans = 0;

        for(int num: num_set){
            //判断num前面有没有紧挨的数字，要是没有，最长序列可能以num作为头
            // 这样做过滤掉诸如[1,2,3,4,5,6]这种情况下的2,3,4,5,6
            if(!num_set.count(num-1)){ 
                int currentNum = num;
                int count = 1;
				
                while(num_set.count(currentNum+1)){// 判断序列是否连续
                    count++;
                    currentNum++;
                }
                ans = max(ans, count);
            }
        }
        return ans;
    }
};

class Solution { //java 代码
    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        int ans = 0;

        for(int i : nums){
            set.add(i);
        }
        // 先找没前驱的数字
        for(int x : set){
            if(set.contains(x-1)){
                continue;
            }
            // 找到没前驱的 开始往后计数
            int y = x + 1;
            while(set.contains(y)){
                y++;
            }
            ans = Math.max(ans, y-x);
        }
        return ans;
    }
}

分析：

• 这里直接用集合去重，省去了代码1里面continue的那一步
• 对于一个数字num，如果存在num-1，即num有前驱，则以num为起点的序列肯定不是最长的
• 遍历set，如果当前的num没有前驱，则以num作为头的序列可能就是最长子序列，这样做过滤掉诸如[1,2,3,4,5,6]这种情况下的2,3,4,5,6
• 所以上一步的遍历set，其实等价于遍历set中所有没有前驱的num开头的序列，在这些有可能达到最大子序列的序列中找出最大长度
• unordered_set 基于哈希表实现，插入操作的平均时间复杂度为 O ( 1 ) O(1) O(1)。遍历长度为 n n n 的数组，每个元素插入一次，总时间复杂度为 O ( n ) O(n) O(n)；当所有元素哈希冲突严重时（例如哈希函数极不均匀），每次插入需要遍历链表，单次插入退化为 O ( n ) O(n) O(n)，总时间复杂度为 O ( n 2 ) O(n²) O(n2)，所以复杂度取决于nums数组，

总结：

• 记住 unordered_set 的实现和使用，比方说num_set.insert(num)
• 代码1比代码2要快一点其实，快排yyds！
• 分析最长子序列的特点：对于一个数字num，如果存在num-1，即num有前驱，则以num为起点的序列肯定不是最长的
• 算法的求解依赖于对数据结构的了解，更依赖于对题目性质的了解！！
• java里面的map是put，set是add

---

双指针

4. 移动零

15min
题目 ：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

代码：双指针

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        int curr = 0;

        for(int i=0; i<nums.size(); i++)
            if(nums[i]) //将非0移动到阡陌数组的末尾 再curr++
                nums[curr++] = nums[i];
        //后面的直接补0
        for(int i=curr; i<nums.size(); i++)
            nums[i] = 0;
    }
};

class Solution { // java代码
    public void moveZeroes(int[] nums) {
        // 双指针
        int i0 = 0;
        for(int i=0; i<nums.length; i++){
            if(nums[i] != 0){
                int t = nums[i0];
                nums[i0] = nums[i];
                nums[i] = t;
                i0++;
            }
        }
    }
}

分析：

• 题目要求可以看作是将0元素拿走之后向左压缩，将数字全推到数组的左边而不改变初始相对位置，后面空出来的直接补0就ok

• 所以可以将0视而不见，curr用于记录已处理非0数组的末尾，i则遍历整个数组(i>=curr)，每当nums[i]非0时，将nums[i]直接放到nums[curr]即可

• 算法设计的过程可以只拿出来中间最典型的重复的片段，比如数组[5, ... , 3, curr, ..., 7, 0, ...],

• 假设双指针curr和i分别指向如图位置和7，curr之前的元素肯定都是非0且满足题意的

• [curr-7)这里面的非0元素肯定已经被复制到curr之前了的，且这一部分的长度等于i已遍历0元素的个数，因为遇到0元素i++，而此时curr保持不动

• i指向7这个非零元素时，直接nums[curr++] = nums[i]

• 而当i指向0元素时，不需要进行处理，我们只在乎非零元素向左移动，当i遍历结束，curr（含）之后的元素除了是0就是已经跑到左面去了，所以后面的直接补0就好

总结：

• 之前做题都想着从头分析，然后脑子很难从头模拟，可以只拿出来最典型的片段进行分析，算法课也是这么讲的
• 关键点：0可以视而不见，只在乎非0的左移，遍历完了剩下的直接补0

---

5. 盛最多水的容器

20min
题目 ：

给定一个长度为n的整数数组height。有n条垂线，第i条线的两个端点是(i, 0)和(i, height[i])。

找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量

代码：双指针

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l=0, r=height.size()-1;
        int ans = 0;

        while(l<r){
            ans = max(ans, min(height[l], height[r])*(r-l));
            if(height[l]<height[r])
                l++;
            else
                r--;
        }
        return ans;
    }
};

class Solution { // java代码
    public int maxArea(int[] height) {
        // 双指针 每次向内移动短板 计算结果并比较
        int i=0;
        int j=height.length - 1;
        int ans = 0;

        while(i<j){
            ans = height[i] < height[j] ? 
                Math.max(ans, (j-i)*height[i++]) : 
                Math.max(ans, (j-i)*height[j--]);
        }

        return ans;
    }
}

分析：

• 水量 = min ( h e i g h t [ l ] , h e i g h t [ r ] ) ∗ ( r − l ) \text{min}(height[l], height[r])*(r-l) min(height[l],height[r])∗(r−l)
• 下一次是左边向右移动还是右边向左移动？
  • 假设 h e i g h t [ l ] < h e i g h t [ r ] height[l]<height[r] height[l]<height[r],此时之间的距离为 ( r − l ) (r-l) (r−l)，此时的容量为 h e i g h t [ l ] ∗ ( r − l ) height[l]*(r-l) height[l]∗(r−l)
  • 当右指针左移一个（高的一边向内移动），此时距离为 ( r − 1 − l ) (r-1-l) (r−1−l)，当：
    • h e i g h t [ r − 1 ] > h e i g h t [ r ] height[r-1] > height[r] height[r−1]>height[r]时， 高度= m i n ( h e i g h t [ l ] , h e i g h t [ r − 1 ] ) = h e i g h t [ l ] = m i n ( h e i g h t [ l ] , h e i g h t [ r ] ) min(height[l], height[r-1]) = height[l] = min(height[l], height[r]) min(height[l],height[r−1])=height[l]=min(height[l],height[r])
    • h e i g h t [ r − 1 ] < h e i g h t [ r ] height[r-1] < height[r] height[r−1]<height[r]时，高度 = m i n ( h e i g h t [ l ] , h e i g h t [ r − 1 ] ) < = m i n ( h e i g h t [ l ] , h e i g h t [ r ] ) min(height[l], height[r-1]) <= min(height[l], height[r]) min(height[l],height[r−1])<=min(height[l],height[r])
  • 综上， m i n ( h e i g h t [ l ] , h e i g h t [ r − 1 ] ) < = m i n ( h e i g h t [ l ] , h e i g h t [ r ] ) min(height[l], height[r-1]) <= min(height[l], height[r]) min(height[l],height[r−1])<=min(height[l],height[r])
  • 所以有： m i n ( h e i g h t [ l ] , h e i g h t [ r − 1 ] ) ∗ ( r − 1 − l ) < m i n ( h e i g h t [ l ] , h e i g h t [ r ] ) ∗ ( r − l ) min(height[l], height[r-1])*(r-1-l) < min(height[l], height[r]) * (r-l) min(height[l],height[r−1])∗(r−1−l)<min(height[l],height[r])∗(r−l)
• 所以，每次都选择高度小的一边向内侧移动

总结

• 看题解不难但是自己证明出来却需要很大的难度，膜而拜之~ orz~

---

6. 三数之和

20min
题目 ：

给你一个整数数组nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

代码：双指针

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int n = nums.size();
        sort(nums.begin(), nums.end());

        vector<vector<int>> ans;

        for(int i=0; i<n; i++){
            if(i>0 && nums[i]==nums[i-1])
                continue;
            int k = n-1;
            int tgt = -nums[i];
            for(int j=i+1; j<n; j++){
                if(j>i+1 && nums[j]==nums[j-1])
                    continue;
                while(j<k && nums[j]+nums[k]>tgt)
                    k--;
                if(j==k) break;
                if(nums[j]+nums[k]==tgt)
                    ans.push_back({nums[i],nums[j], nums[k]});

            }
        }
        return ans;
    }
};

class Solution { // java代码
    public List<List<Integer>> threeSum(int[] nums) {
        // 排序后 先去重 当num[i]>0的时候break 然后左右指针LR
        // 判断 去重 L++ R--
        List<List<Integer>> ans = new ArrayList<>();
        int len = nums.length;
        if(len<3) return ans;
        Arrays.sort(nums);

        for(int i=0; i<len; i++){
            if(nums[i] > 0) break;
            if(i>0 && nums[i]==nums[i-1]) continue;
            int L = i+1;
            int R = len-1;
            while(L<R){
                int sum = nums[i]+nums[L]+nums[R];
                if(sum == 0){
                    ans.add(Arrays.asList(nums[i], nums[L], nums[R]));
                    // 这里内部去重
                    while(L < R && nums[L]==nums[L+1]) L++;
                    while(L < R && nums[R]==nums[R-1]) R--;
                    L++; R--;
                }
                else if(sum<0) L++;
                else if(sum>0) R--;
            }
        }
        return ans;
    }
}

分析：

• 传统做法是三重i, j, k遍历+去重，复杂度 O ( n 3 ) O(n^3) O(n3)
• 所以在刚开始做的时候就要考虑去重，即相同的组合不能出现第二次，可以先排序，保证更里面一重循环遍历的元素大于等外一层循环遍历当前指向的元素，这样将最外层循环指向的元素作为目标元素tgt-nums[i]，当-tgt==nums[j]+nums[k]时即为我们想找的目标
• 里面两层遍历？等等，这是不是两数之和，所以可以优化，因为已经排好序了，里面的遍历不就可以前后指针遍历，当nums[j]+nums[k]>tgt时k--靠近目标就好了

总结

• vector<vector<int>> ans 而不是 int vector<vector<int>> ans
• ans.push_back({nums[i],nums[j], nums[k]}); {圈养}起来再push

---

7. 接雨水

20min
题目 ：

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

代码1：动态规划

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();

        vector<int> lmax(n);
        lmax[0] = height[0];
        for(int i=1; i<n; i++)
            lmax[i] = max(lmax[i-1], height[i]);

        vector<int> rmax(n);
        rmax[n-1] = height[n-1];
        for(int i=n-2; i>=0; i--)
            rmax[i] = max(rmax[i+1], height[i]);

        int ans = 0;
        for(int i=0; i<n; i++)
            ans += min(lmax[i], rmax[i]) - height[i];

        return ans;
    }
};

class Solution { // java 代码
    public int trap(int[] height) {
        // 接雨水 动态规划 按列求
        // 每个height的水等于min(lmax, rmax) - h
        int n = height.length;
        int[] lmax = new int[n];
        int[] rmax = new int[n];
        
        lmax[0] = height[0];
        for(int i=1; i<n; i++){
            lmax[i] = Math.max(lmax[i-1], height[i-1]);
        }

        rmax[n-1] = height[n-1];
        for(int i=n-2; i>=0; i--){
            rmax[i] = Math.max(rmax[i+1], height[i+1]);
        }

        int ans=0;
        for(int i=0; i<n; i++){
            int min=Math.min(lmax[i], rmax[i]);
            if(min > height[i]){
                ans += min-height[i];
            }
        }

        return ans;
    }
}

分析 ：

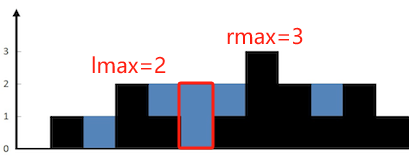
• 看图可知，每个位置i处所能接得的水量等于min(max(左柱子), max(右柱子))-height[i]
• 举个例子，红框所能接得的水量=min(lmax, rmax) - height[i] = min(2, 3) - 0 = 2
• 所以，只需要找到每个位置i的lmax和rmax就ok
• 边界分析：最两边其实是接不上水的，所以两边的lmax和rmax等于自己的高度就好，那么第二个循环为什么从n-2开始呢？哦~，元素总数为n，只能遍历到n-1，n-1的位置又已经被初始化，所以就从n-2开始啦
• 复杂度分析：线性遍历 O ( n ) O(n) O(n)

代码2：双指针

class Solution {
public:
    int trap(vector<int>& height) {
        int l = 0;
        int r = height.size() - 1;
        int lmax=0, rmax=0, ans=0;
        while(l<r){
            lmax = max(lmax, height[l]);
            rmax = max(rmax, height[r]);
            if(lmax<rmax){
                ans += lmax-height[l];
                l++;
            }
            else{
                ans += rmax-height[r];
                r--;
            }
        }
        return ans;
    }
};

class Solution { // java 代码
    public int trap(int[] height) {
        // 接雨水 双指针
        // 动态维护lmax 和 rmax
        int n = height.length;
        int l = 0; 
        int r = n - 1;
        int lmax = 0;
        int rmax = 0;
        int ans=0;
        
        while(l<r){
            lmax = Math.max(lmax, height[l]);
            rmax = Math.max(rmax, height[r]);
            if(lmax < rmax){
                ans +=  lmax-height[l];
                l++;
            }else{
                ans += rmax-height[r];
                r--;
            }
        }
        return ans;
    }
}

分析：

• 动态规划做法是分别计算当前位置i两边柱子的最大高度，水量是一次性计算出来的
• 但是双指针可以边更新两边的最大高度，或者说根据柱子的高度，计算当前位置的水量
• 当位置i的lmax<rmax时，说明当前位置是可能存水的地方，为什么是可能呢？当height[i]==lmax，这个地方肯定存不下水，当height[i]<lmax时，从左到右就存在了一个"下坡"，也就是lmax在位置i的左边是可以挡水的，又因为lmax<rmax，rmax高rmax也可以挡水，左右都能挡住水，这个时候 位置i就能存水了

总结

• 解题关键是知道要求左右高度最大值的最小值，需要将问题转化为简单通俗的实际需求，也就是找到另一种问题表述

---

滑动窗口

8. 无重复的最长子串

20min
题目 ：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。
代码：滑动窗口（其实也有点像双指针）

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_set<char> dict;
        int n = s.size();
        int j=0, ans=0;
        for(int i=0; i<n; i++){
            if(i != 0)
                dict.erase(s[i-1]);
            while(j<n && !dict.count(s[j])){
                dict.insert(s[j]);
                j++;
            }
            ans = max(ans, j-i);
        }
        return ans;
    }
};

class Solution { // java代码
    public int lengthOfLongestSubstring(String s) {
        // 无重复字符最长子串
        // hash表快速查到重复位置
        int n = s.length();
        if(n==0) return 0;
        int ans = 0;
        int left = 0;

        HashMap<Character, Integer> dict = new HashMap<>();

        for(int i=0; i<n; i++){
            if(dict.containsKey(s.charAt(i))){
                left = Math.max(left, dict.get(s.charAt(i))+1);
            }
            dict.put(s.charAt(i), i);
            ans = Math.max(ans, i-left+1);
        }
        return ans;
    }
}

分析：

• 常规简单思路：固定以i为串头，滑动j为串尾挨个往后找，只要不重复，长度ans++，只要重复了，ans清零，再以i后面的元素作为串头重复这个过程，直到遍历完所有不重复子串
• 怎么知道重复不重复？我们有unordered_set<char> dict，我们知道set里面的东西都是不重复的，边往后找边插入，插入之前判断一下重复没就ok dict.count(s[j])
• 重复的判定？我们已经知道当dict.count(s[j])非零则出现重复，准确点说，是当前的串头和串尾出现了重复，此时不看串头，剩下的子串依旧是满足我们要求的，所以当出现重复时，我们可以在set中抹掉重复的串头，从上次的串尾继续往后看

总结

• 说和双指针类似是因为i, j也是根据条件滑动的，双指针一般是左右向中间靠，这里是都往右边走，归根结底还是两个指针
• 数据结构只是工具，最关键的是针对问题的建模和理解，找出最核心不变的特征，最后就是一个重复的过程，重复之中找永恒

---

9. 找到字符串中所有字母异位词

30min
题目 ：

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。
代码：滑动窗口

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        int ls=s.size(), lp=p.size();
        vector<int> ans;
        if(ls<lp)
            return ans;
        
        vector<int> cnts(26);
        vector<int> cntp(26);
        for(int i=0; i<lp; i++){
            cnts[s[i]-'a']++;
            cntp[p[i]-'a']++;
        }

        if(cnts == cntp)
            ans.emplace_back(0);
        for(int i=0; i<ls-lp; i++){
            cnts[s[i]-'a']--;
            cnts[s[i+lp]-'a']++;
            if(cntp == cnts)
                ans.emplace_back(i+1);
        }
        return ans;
    }
};

class Solution { // java代码
    public List<Integer> findAnagrams(String s, String p) {
        // 找字符串中所有的异位词 出现的地方
        // 定长滑窗 没每个子串姊妹出现的次数和 p是否相等 
        // 每次右侧滑进 左侧弹出
        int ls = s.length();
        int lp = p.length();
        List<Integer> ans = new ArrayList<>();
        if (ls < lp) return ans;
        int[] cnts = new int[26];
        int[] cntp = new int[26];
        for(char c : p.toCharArray()){
            cntp[c-'a']++;
        }
        
        for(int i=0; i<ls; i++){
            cnts[s.charAt(i)-'a']++;
            if(i>=lp){ // 出窗
                cnts[s.charAt(i-lp)-'a']--;
            }
            if(Arrays.equals(cntp, cnts)){
                ans.add(i-lp+1);
            }
        }
        return ans;
    }
}

分析：

• 字母异位词：长度相等 ，同一字母出现的次数相等
• 知道了字母异位词很容易就知道这是一道关于滑动窗口的题目，p作为目标窗口，找一个和p大小相同的滑动窗口从头往后滑动
• 怎么匹配滑动窗口和目标窗口？答：数组。用数组统计词频最后比较两个窗口是否一致就ok
• 最后一个for：滑动窗口的长度是固定的，滑进来一个自然滑出去一个 ~
• i<ls-lp ： 防止窗口越界，这个长度正好是一个窗口的长度

总结

• 理解什么是字母异位词后面的就好说一点了，加油加油！！！