"不确定性椭球"的深度解析
这是一个极其重要的概念，它把抽象的协方差矩阵转化为直观的几何图像。
一、基本思想：从点到区域
当您进行测量平差（如GNSS定位）后，您得到的是一个点估计 ------比如三维坐标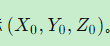
但真实值可能在这个点附近的位置，形成一个可能分布的区域。
"不确定性椭球"就是这个可能区域的几何描述：
-
椭球中心：平差值（点估计）
-
椭球形状：由协方差矩阵决定
-
椭球大小 ：由单位权中误差
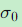缩放 -
椭球方向：由参数间的相关性决定
二、数学本质：协方差矩阵的几何解释
三、从一维到三维的理解
1. 一维情况（标量）
2. 二维情况（平面）
3. 三维情况（空间）
四、特征值与特征向量的几何意义
物理意义：
五、在AGNSS中的具体应用
1. GNSS单点定位的误差椭球
3. 提取实用的精度指标
从误差椭圆/椭球提取常用指标：
水平精度指标
六、协因数阵 Q 的作用
七、实例：GNSS定位的误差椭球分析
场景：静态单点定位，观测了8颗卫星
计算步骤：
# Python示例代码
import numpy as np
# 假设的协方差矩阵（单位：m²）
D_xyz = np.array([[0.25, 0.12, 0.08],
[0.12, 0.36, -0.05],
[0.08, -0.05, 0.64]])
# 特征分解
eigenvalues, eigenvectors = np.linalg.eig(D_xyz)
# 排序特征值从大到小
idx = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
print("特征值（方差）：", eigenvalues)
print("特征向量（主轴方向）：")
print(eigenvectors)
# 椭球主轴长度（k=1，1σ）
axis_lengths = np.sqrt(eigenvalues)
print("椭球主轴长度（1σ）：", axis_lengths)-
结果解释：
-
假设得到特征值：[0.70, 0.30, 0.25]
-
主轴长度：[0.84m, 0.55m, 0.50m]
-
这表示：
-
最长的不确定性方向有0.84m的标准差
-
最短的不确定性方向有0.50m的标准差
-
椭球体积反映整体精度# 旋转矩阵（假设测站在纬度30°，经度120°）
-
-
lat = np.radians(30)
lon = np.radians(120)
R = np.array([
[-np.sin(lon), np.cos(lon), 0],
[-np.sin(lat)*np.cos(lon), -np.sin(lat)*np.sin(lon), np.cos(lat)],
[np.cos(lat)*np.cos(lon), np.cos(lat)*np.sin(lon), np.sin(lat)]
])
D_enu = R @ D_xyz @ R.T
print("ENU系协方差矩阵：")
print(D_enu)
# 提取水平和高程精度
sigma_E = np.sqrt(D_enu[0, 0]) # 东向中误差
sigma_N = np.sqrt(D_enu[1, 1]) # 北向中误差
sigma_U = np.sqrt(D_enu[2, 2]) # 天向中误差
print(f"东向精度：{sigma_E:.3f} m")
print(f"北向精度：{sigma_N:.3f} m")
print(f"天向精度：{sigma_U:.3f} m")
print(f"水平精度（DRMS）：{np.sqrt(sigma_E**2 + sigma_N**2):.3f} m")八、为什么是"椭球"而不是"球"？
-
各向异性：不同方向的不确定性通常不同
-
垂直方向（U）通常比水平方向精度差
-
特定水平方向可能因卫星几何构型而变差
-
-
相关性导致倾斜：参数间的相关性使椭球主轴不平行于坐标轴
- 例如：接收机钟差误差与高程误差强相关，导致椭球在Z-Δt平面倾斜
-
卫星几何的影响：
-
好的卫星分布 → 接近球形的椭球（各方向精度均匀）
-
差的卫星分布 → 扁长的椭球（某些方向精度很差）
-
这就是DOP值的几何意义：描述椭球的"扁长"程度
-
九、不确定性椭球的实际意义
对AGNSS开发者的价值：
-
可视化精度：将抽象的协方差矩阵转化为直观的几何图像
-
诊断工具：
-
扁长的椭球 → 卫星几何构型差
-
过大的椭球 → 观测质量差或模型问题
-
异常的倾斜 → 参数强相关，可能需要重新参数化
-
-
设计指导：
-
评估不同观测方案能达到的精度
-
优化卫星选择策略
-
设计可靠性监测算法
-
在完好性监测中的应用：
误差椭球是保护等级计算的基础：
-
水平保护等级（HPL）：通常取误差椭圆的长半轴或外接圆半径
-
垂直保护等级（VPL）：误差椭球在垂直方向的投影
十、总结与核心要点
不确定性椭球的本质：
-
它是协方差矩阵的几何表现
-
描述了参数估计值的可能分布区域
-
形状由平差模型决定（Q）
-
大小 由观测质量决定
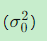
关键特性：
-
主轴方向：最确定和最不确定的方向
-
主轴长度：各方向的标准差（乘以k后对应特定置信度）
-
体积：整体精度指标（与GDOP相关）
-
方向性：反映了参数间的相关性
在GNSS中的具体体现：
-
三维误差椭球：XYZ坐标系下的精度分布
-
误差椭圆：水平面内的精度分布
-
精度指标：CEP、DRMS等都是从误差椭圆/椭球导出的简化指标
理解"不确定性椭球"的概念，能让您从简单的精度数字（如"水平精度1.5m"）深入到精度的完整空间分布特性。这对于开发高精度AGNSS系统、设计完好性算法、以及优化定位性能都至关重要。
这就像从只知道"房间有多大"（一个数字），进步到知道"房间的具体形状、长宽高、以及哪个方向最窄、哪个方向最宽"（完整的几何信息）。后者无疑提供了更丰富、更有用的信息。