最近身体不适,所以训练上比较缺乏动力,下面是vp这场的一个个人笔记。
快捷导航栏:
A
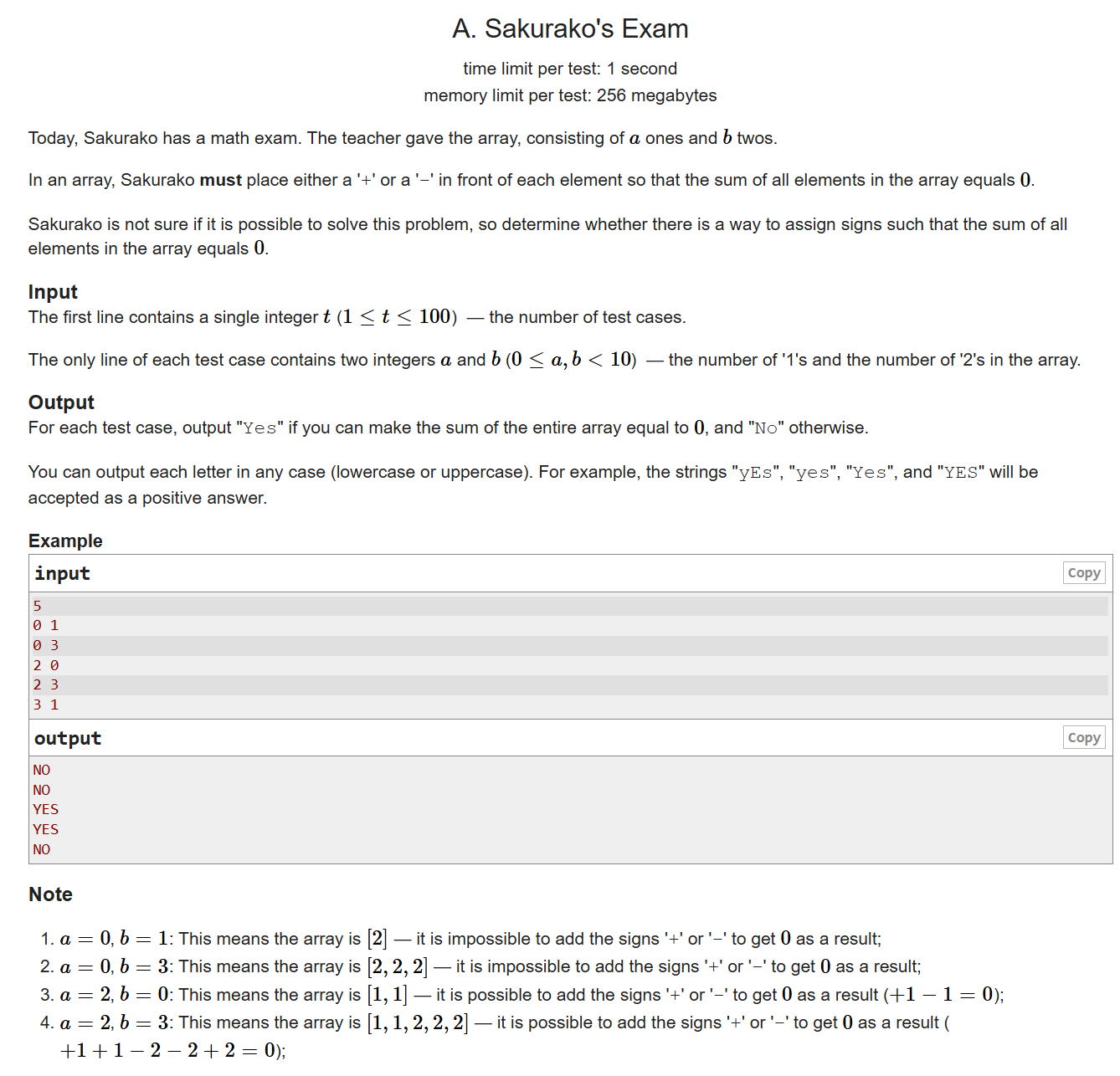
简单的数学题,没啥说的,直接上代码:
cpp
#include<bits/stdc++.h>
using namespace std;
void solve(){
int a,b;
cin>>a>>b;
if(a>=2&&b%2==1){
a-=2;
b++;
}
if(a%2==0&&b%2==0)
cout<<"YES"<<'\n';
else
cout<<"NO"<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}B:
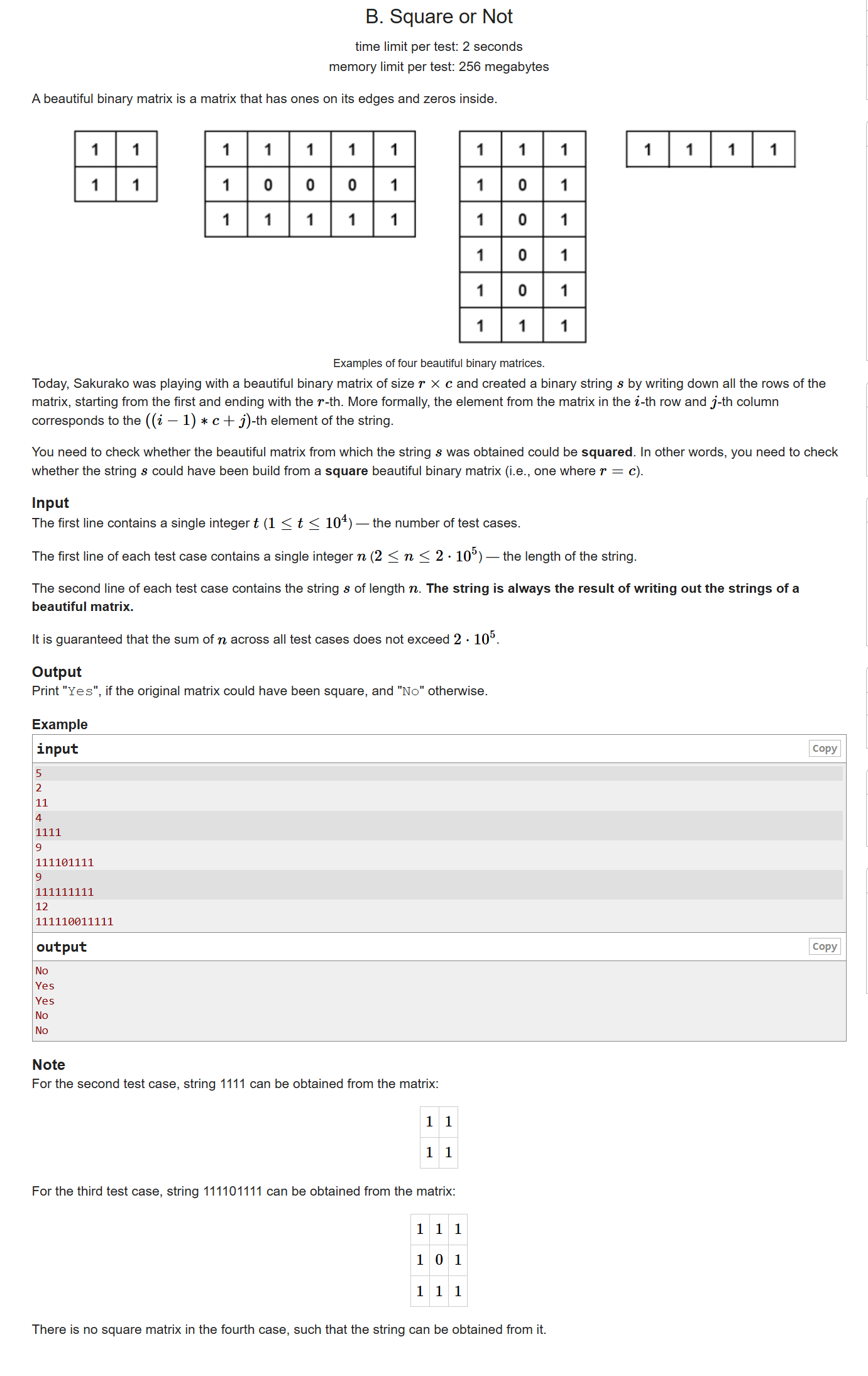
首先,要读懂题(当时我有点着急,没读懂题),然后直接判断即可,没啥难度。
cpp
#include<bits/stdc++.h>
using namespace std;
void solve(){
string s;
int n;
cin>>n>>s;
int l=sqrt(n);
bool r=false;
if(l*l==n){
r=true;
for(int i=0;i<s.size();i++){
if(i<l||i>=l*(l-1)||i%l==0||(i+1)%l==0){
if(s[i]=='0')
r=false;
}else if(s[i]=='1')
r=false;
}
}
if(r)
cout<<"YES"<<'\n';
else
cout<<"NO"<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}C:
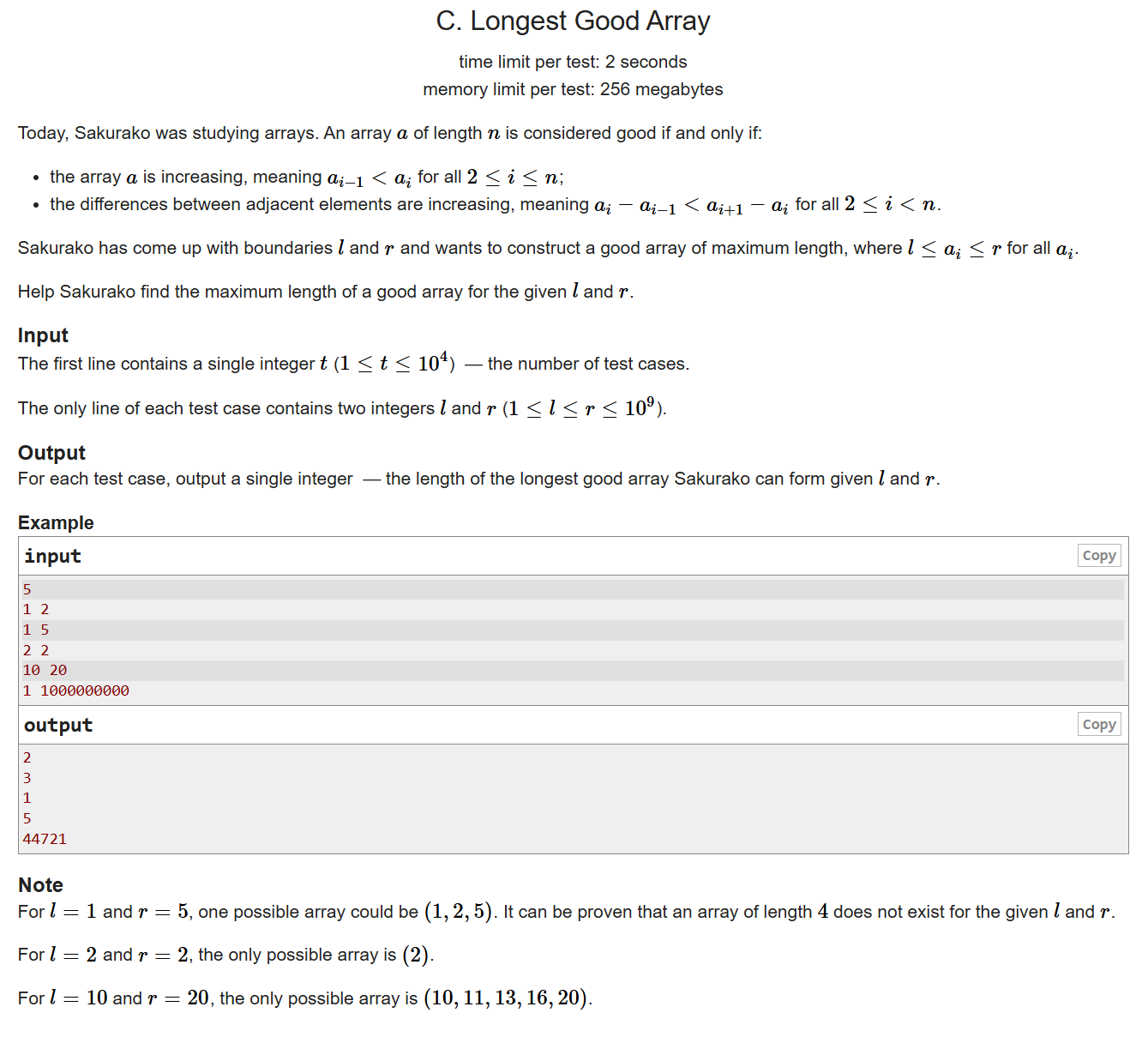
简单的模拟,让 ,
开始,进行
,
不断的循环,看能进行几次即可。
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
ll d=1;
ll l,r;
ll ans=0;
cin>>l>>r;
while(l<=r){
ans++;
l+=d;
d++;
}
cout<<ans<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}D:

我们把所有能连成环的看成一个集合,然后这个集合内的答案都一样,简单模拟即可。
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+100;
int p[N];
string s;
int ans[N];
int n;
void init(){
for(int i=1;i<=n;i++){
ans[i]=-1;
}
}
void find(int st){
int cnt=0;
int ne=st;
vector<int>a;
while(1){
if(s[ne]=='0')
cnt++;
a.push_back(ne);
ne=p[ne];
if(ne==st)
break;
}
for(auto c:a)
ans[c]=cnt;
}
void print(){
for(int i=1;i<=n;i++)
cout<<ans[i]<<' ';
cout<<'\n';
}
void solve(){
cin>>n;
init();
for(int i=1;i<=n;i++)
cin>>p[i];
cin>>s;
s=" "+s;
for(int i=1;i<=n;i++){
if(ans[i]==-1){
find(i);
}
}
print();
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}E:
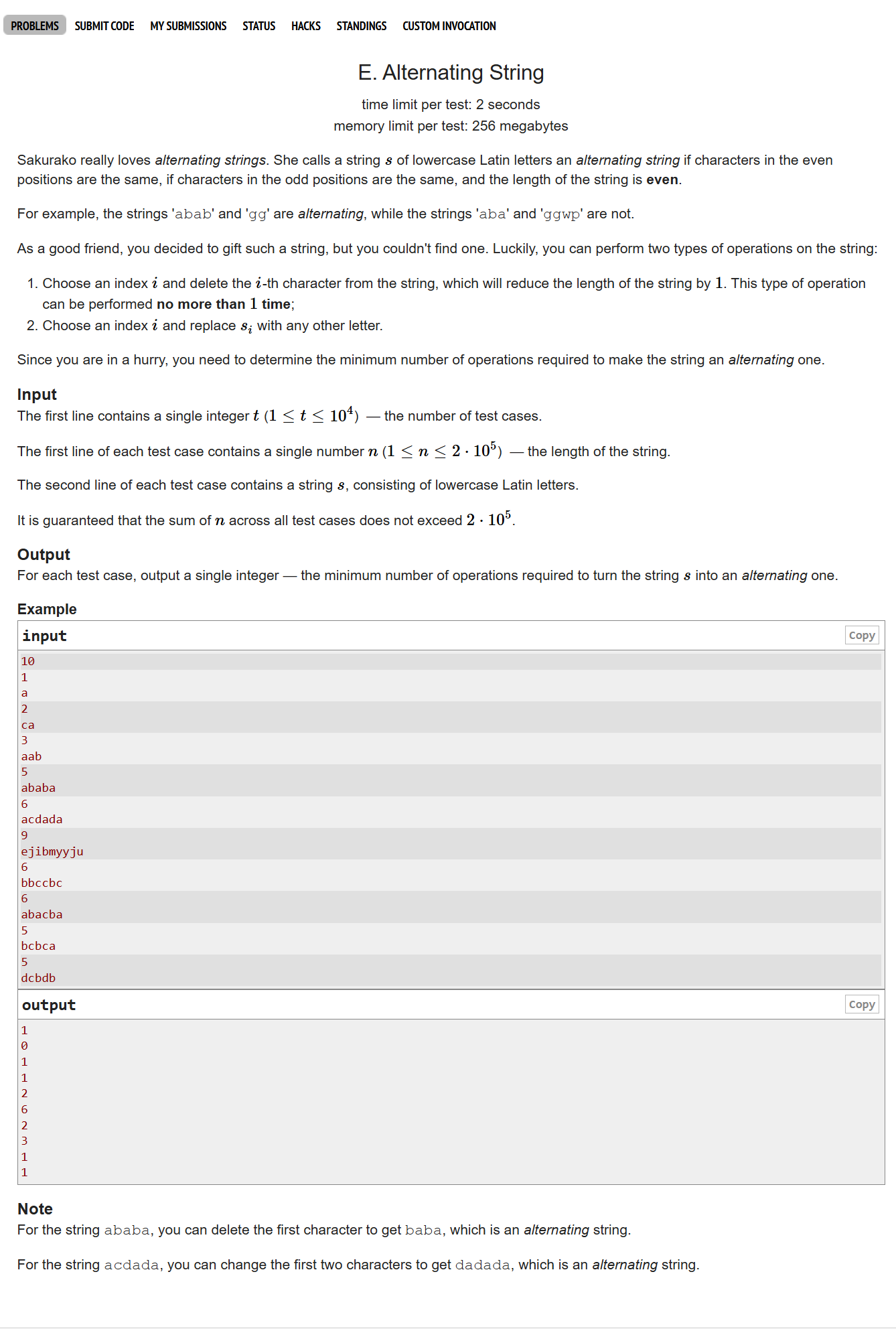
有一个特性,如果字符串长度为偶数,那么直接看当前字符串的最优策略即可。
否则就要枚举删除任意一个字符后的最优结果,可以用 奇偶前缀和(对每一个下标只记录前面与其同奇偶下标的结果,比如 ,
之类)来统计字符串结果。
假设要删除下标 ,那么有以下两种情况:
(1) 为奇数,若想统计删除该下标后 拼接字符串为奇数的下标,即可用
这类式子表示,若想统计 删除该下标后 拼接字符串为 奇数的下标,即可用
这类式子表示。
(2) 为偶数,若想统计删除该下标后 拼接字符串为奇数的下标,即可用
这类式子表示,若想统计 删除该下标后 拼接字符串为 奇数的下标,即可用
这类式子表示。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+100;
int pre[N][26];
int n;
string s;
int ans;
void print(int id){
int len=n/2;
int x1,x2;
x1=x2=1e9;
if(id==n+1){
for(int j=0;j<26;j++)
x1=min(x1,len-pre[n][j]);
for(int j=0;j<26;j++)
x2=min(x2,len-pre[n-1][j]);
ans=x1+x2;
}else{
for(int j=0;j<26;j++){//奇数下标
int c;
if(id%2==0){
c=pre[n-1][j]-pre[id][j]+pre[id-1][j];
}else{
c=pre[n-1][j]-pre[id-1][j]+pre[max(id-2,0)][j];
}
x1=min(x1,len-c);
}
for(int j=0;j<26;j++){// 偶数下标
int c;
if(id%2==0){
c=pre[n][j]-pre[id-1][j]+pre[id-2][j];
}else{
c=pre[n][j]-pre[id][j]+pre[id-1][j];
}
x2=min(x2,len-c);
}
ans=min(ans,x1+x2+1);
}
}
void solve(){
cin>>n;
cin>>s;
s=" "+s;
ans=1e9;
for(int i=1;i<=n;i++){
if(i==1){
for(int j=0;j<26;j++)
pre[i][j]=pre[i-1][j];
}else{
for(int j=0;j<26;j++)
pre[i][j]=pre[i-2][j];
}
pre[i][s[i]-'a']++;
}
if(n%2==0){
print(n+1);
}else{
for(int i=1;i<=n;i++)
print(i);
}
cout<<ans<<'\n';
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}F:

这道题其实挺简单的,我们知道求这个分为分子和分母,分子部分其实就是 上述数组每两个数的 相互乘起来的和,分母其实就是 ,求分子根据以下式子拆分即可:
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
ll n;
ll qmi(ll a,ll b,ll c){
ll res=1;
a=a%mod;
while(b){
if(b&1)
res=res*a%c;
a=a*a%c;
b>>=1;
}
return res;
}
void solve(){
cin>>n;
ll x,y;
x=y=0;
for(int i=1;i<=n;i++){
ll a;
cin>>a;
x=(x+a%mod)%mod;
y=(y+a*a%mod)%mod;
}
ll ans=(((x*x)%mod-y%mod)%mod+mod)%mod;
ans=ans*qmi(n*(n-1)%mod,mod-2,mod)%mod;
cout<<ans<<'\n';
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}G:

思路:
首先,他的操作和 欧几里得求 是同一个道理,下面来浅浅的解释一下:
当 的时候,若想要
尽可能大,最优策略肯定是让这两个数尽可能小到不能再小且不相等,这样才能保证最终答案尽最大可能的大。因此对于较大的
,可以一直使用
让其变化,直至
,再继续对
操作,然后依次重复,这个过程上其实相当于
,
,这其实和 欧几里得求
的过程一样,最终可以得到
和
这两个数。
当 的时候,其本质也是不断求
的过程,最终数列的每个数都可以变成
的倍数。
所以我们可以构造一个满足如下要求的数列:
然后就是简单的判断 在固定的数列下在哪里即可。
注意,当 的时候需要特殊判断一下。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+100;
ll a[N];
ll n,k;
/*
0 1 2 3 4 c-1
c c+1 c+2 .. 2*c-1
*/
void solve(){
cin>>n>>k;
ll c=0,ans=0;
for(int i=1;i<=n;i++){
cin>>a[i];
c=__gcd(c,a[i]);
}
if(n==1){
if(a[1]>=k)
cout<<k-1<<'\n';
else
cout<<k<<'\n';
return ;
}
for(int i=1;i<=n;i++){
a[i]=(i-1)*c;
}
for(int i=1;i<=n;i++){
if(ans+k<a[i]){
break;
}
ll d=min(c-1,k);
k-=d;
ans=a[i]+d;
}
if(k)
ans+=k;
cout<<ans<<'\n';
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}H:

思路:
我们分析一下这道题,看看数据范围,对于查询的 以及
都是很明显要
的,又有查询,所以多半是要进行预处理这一步操作的。
我们先不处理每个查询,而是先把所有可能的查询所得到的结果都先存储起来,最后以
的复杂度来处理每次查询。
对于一个固定的 ,我们对于数组的每个元素
,若想让中位数尽可能小,就要让每个
,如果直接遍历数组的话,时间复杂度为
会超时,因此需要优化一下。这里可以利用一下
的性质,统计每一个
出现的次数,设
为
在数组中出现的次数,对于
对于的答案
,其必然满足
,且
,因此我们可以前缀和处理一下
,然后对于
,可以通过二分来找到答案。
最后根据以上思路进行代码实现即可。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+100;
int cnt[N],ans[N];
int n,q;
void init(){
for(int i=0;i<=n;i++){
cnt[i]=ans[i]=0;
}
}
void solve(){
cin>>n>>q;
init();
for(int i=1;i<=n;i++){
int x;
cin>>x;
cnt[x]++;
}
for(int i=1;i<=n;i++)
cnt[i]+=cnt[i-1];
for(int x=1;x<=n;x++){//存储 查询为 x的答案
int l=0,r=x;
int res=x;
while(l<=r){
int mid=(l+r)/2,sum=cnt[mid];
for(int k=1;k*x<=n;k++){
sum+=cnt[min(k*x+mid,n)]-cnt[k*x-1];
}
if(sum-1>=n/2){
res=mid;
r=mid-1;
}else
l=mid+1;
}
ans[x]=res;
}
while(q--){
int x;
cin>>x;
cout<<ans[x]<<' ';
}
cout<<'\n';
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}