突破无人机检测瓶颈!基于EMD/EEMD与机器学习的射频指纹分解新方案
一、题目
基于机器学习的微型无人机检测中的自适应射频指纹分解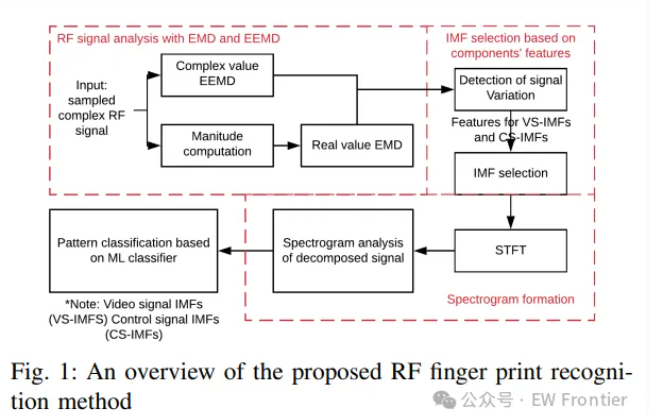
二、摘要
射频(RF)信号分类已广泛应用于未知无人机(UAV)的特征检测与识别。本文提出一种基于经验模态分解(EMD)和集合经验模态分解(EEMD)的方法,用于提取入侵无人机的通信信道特征。选取分解后去除噪声成分的固有模态函数(IMF),结合机器学习(ML)进行射频信号模式识别。分类结果表明,EMD和EEMD带来的去噪效果均能提升不同射频通信信道特征下的检测精度,尤其在识别时变射频信号源方面表现突出。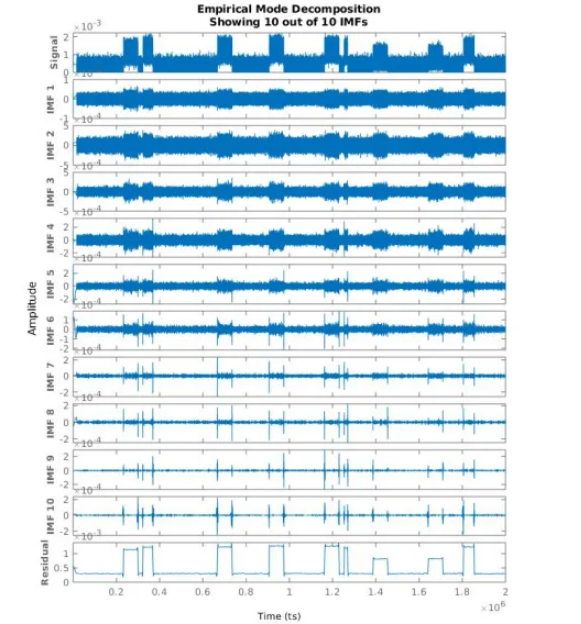
三、引言
近年来,控制技术与材料技术的进步使微型无人机系统(UAS)的可靠性显著提升。随着民用无人机价格下降,其市场规模持续扩大,但同时也给机场、核电站、变压器等敏感设施带来了迫切的安全威胁,导致相关区域空域安全性降低[1]-[4]。
多普勒雷达已被用于微型无人机检测研究多年[5]-[7],由螺旋桨旋转产生的微多普勒特征已有效应用于未知无人机检测[8]-[10]。在相关研究[11]-[12]中,研究者表明短时傅里叶变换(STFT)和快速傅里叶变换(FFT)可通过长时间信号采样,有效估计微型无人机的螺旋桨旋转特征、转速及桨叶物理参数。然而,有源雷达的监视空域有限,导致其频谱分辨率较低,难以实现远距离检测。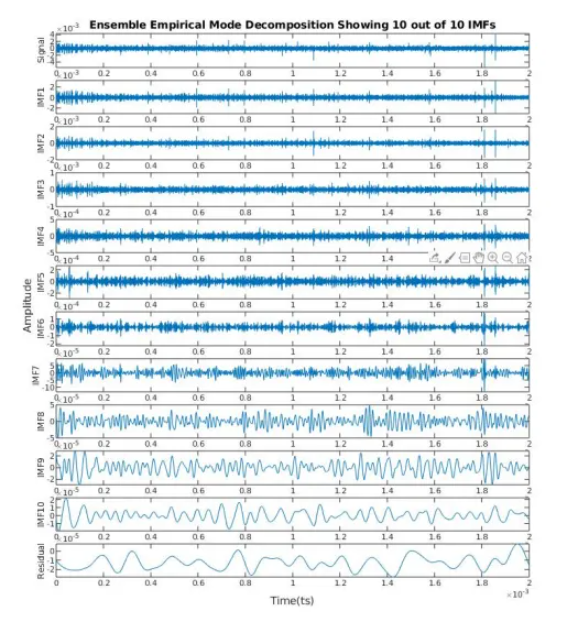
射频指纹也被用作微型无人机检测的主要依据。部分研究[13]-[15]、[20]采用传统STFT与机器学习算法,获取无人机存在时的时频能量谱模式;研究[16]通过室内实验探讨了静态射频源检测方法,用于识别入侵无人机的数量。由于射频通信具有散射传输与接收的特性,短时信号采样并不会影响基于射频的远距离检测效果,但低信噪比(SNR)和日益复杂的无线信号环境仍是主要挑战。
与传统傅里叶变换相比,经验模态分解(EMD)在抑制无人机机身振动、环境干扰产生的噪声方面更具优势[11]。研究[9]通过选取固有模态函数(IMF),从微多普勒特征(m-DS)中提取了六种常用熵特征,结果表明这些特征组合可有效识别无人机的存在;研究[8]探讨了利用EMD重构螺旋桨旋转信号,以区分微型无人机微多普勒特征的可能性。
受上述两种接收信号去噪方法的启发,本文提出将EMD和EEMD应用于入侵无人机射频指纹特征提取,实现远距离无人机检测。选取分解后去除噪声成分的固有模态函数(IMF),结合机器学习进行射频信号模式识别。最后,通过训练卷积神经网络(CNN)、多层感知器(MLP)、决策树、支持向量机(SVM)等多种机器学习分类器,对比EMD和EEMD对接收信号数据的去噪性能。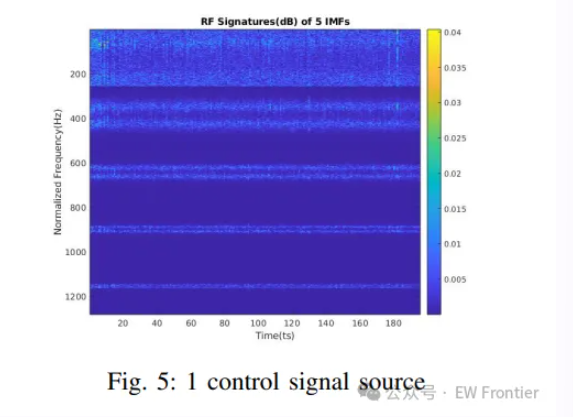
四、方法简介
本文提出的微型无人机时变射频信号模式获取方法整体框架如图1所示。首先,通过对接收的复信号进行变换,得到两种类型的固有模态函数(CS-IMFs和VS-IMFs);随后选取非噪声且具有特征的固有模态函数,通过短时傅里叶变换(STFT)构建时频能量谱;最后利用机器学习分类器,基于接收的射频信号模式识别入侵无人机。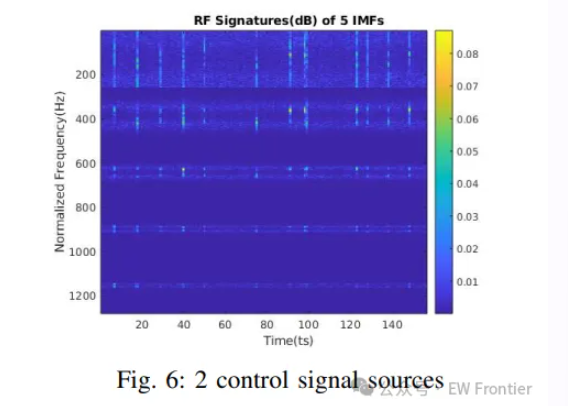
(一)EMD与EEMD
经验模态分解(EMD)由Huang等人[17]首次提出,是一种数据驱动的非线性、非平稳信号分析方法。作为一种自适应方法,EMD可将时间序列数据分解为一组固有模态函数(IMF),这些函数构成信号表示的基,且大多能物理意义明确地反映潜在过程,无需谐波假设[18],其数学表达式如下:
f(n)=∑k=1KIMFsk(ck)+r(n)f(n)=\sum_{k=1}^{K} I M F s_{k}\left(c_{k}\right)+r(n)f(n)=∑k=1KIMFsk(ck)+r(n)
其中, IMFsk(n)IMFs_k(n)IMFsk(n) 表示第k个固有模态函数(IMF),对应频率成分 ckc_kck , r(n)r(n)r(n) 为局部极值与最终分解的IMF信号之间的残差,本文中K取值为10。
固有模态函数与残差函数的线性组合构成分解后的信号,固有模态函数的获取过程可通过以下公式说明:
hi(n)=f(n)−mi(n)h_{i}(n)=f(n)-m_{i}(n)hi(n)=f(n)−mi(n)
其中, mi(n)m_i(n)mi(n) 为上包络与下包络的平均值, hi(n)h_i(n)hi(n) 为潜在固有模态函数,需满足以下筛选准则:
Stdi=∑n=0Nhi−1(n)−hi(n)2hi−12(n)Std {i}=\sum{n=0}^{N} \frac{h_{i-1}(n)-h_{i}(n)^{2}}{h_{i-1}^{2}(n)}Stdi=∑n=0Nhi−12(n)hi−1(n)−hi(n)2
式中, StdiStd_iStdi 表示 hi−1h_{i-1}hi−1 差值率之和的标准差,当 StdiStd_iStdi 小于设定阈值时,即可定义该潜在函数为固有模态函数(IMF)。
然而,受信号极值点分布不均的影响,EMD存在模态混叠的分解缺陷。集合经验模态分解(EEMD)[19]则解决了这一问题,其将真实固有模态函数定义为多次试验结果的均值,具体步骤如下:
-
向目标时间序列数据 f(n)f(n)f(n) 中添加有限幅度的白噪声序列 w(n)w(n)w(n) ,并将其分解为固有模态函数(IMF);
-
多次重复步骤1,每次添加不同的白噪声序列,对分解得到的对应固有模态函数进行集合平均,得到最终的固有模态函数(IMF)。
图2展示了对微型无人机2.4G上行链路信号的EMD分解结果,第10个IMF仍与原始信号保持相同的触发沿,这表明EMD在有限数量的IMF分解下无法充分提取数据包传输特征信号,即存在模态混叠现象。而EEMD对微型无人机与遥控器之间2.4G上行链路信号的分解在第5个IMF时已能体现核心特征,第6至10个IMF则接近白噪声特性(无无人机通信链路数据包传输时,这些IMF主要由噪声成分主导),因此选取第1至5个IMF通过STFT进行后续模式构建。
(二)基于固有模态函数(IMF)的短时傅里叶变换(STFT)
短时傅里叶变换(STFT)通过计算信号幅度获取固有模态函数(IMF)的频谱图,其数学表达式如下:
STFT(f,t)=∑n=−∞∞s(t)w(t−m)e−j2πkn/NSTFT(f, t)=\sum_{n=-\infty}^{\infty} s(t) w(t-m) e^{-j 2 \pi k n / N}STFT(f,t)=∑n=−∞∞s(t)w(t−m)e−j2πkn/N
其中, s(t)s(t)s(t) 表示每个IMF对应的信号( s(t)=IMFss(t)=IMFss(t)=IMFs ), w(t)w(t)w(t) 为离散窗函数,n为采样点数,N为傅里叶变换分析窗长度,m为分析窗位置(满足 m(i−1)=m(i)+nNm(i-1)=m(i)+nNm(i−1)=m(i)+nN ),k为频率成分索引(对应 kw0kw_0kw0 ,且 w0=2πfs/Nw_0=2\pi f_s/Nw0=2πfs/N )。
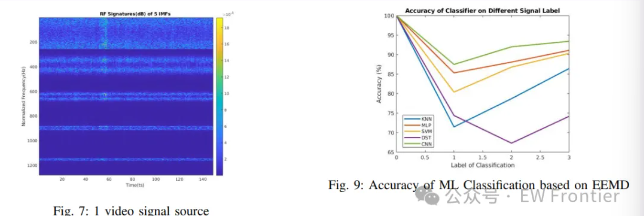
为观察不同固有模态函数的时频谱特征,对每个IMF进行短时傅里叶变换(STFT),获取信号的时频能量分布,以突出识别信号的特征。实验结果显示,EEMD分解后,第1至5个IMF的主成分在时域上具有稳定的信号强度,且能清晰区分数据包传输特征(如图5-7所示),甚至可识别多个控制信号源,为多无人机检测提供了可能。
五、结论
本文提出了一种将EMD和EEMD信号分解应用于微型无人机检测的新方法。该方法将带宽有限的无人机控制信号与视频信号分解为多组固有模态函数(IMF),每个固有模态函数对应无人机与遥控器通信链路中的不同频率成分。通过不同机器学习分类器对固有模态函数构建的模式进行分类,结果显示两种方法在区分无人机射频通信信道不同特征方面具有显著优势,检测精度大幅提升。