【数据结构】假如数据排排坐：顺序表的秩序世界

🔭 个人主页：散峰而望

《C语言：从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月，不做归山云

🎬博主简介

【数据结构】假如数据排排坐：顺序表的秩序世界

前言
[1. 线性表](#1. 线性表)
[2. 顺序表](#2. 顺序表)
- [2.1 概念及其结构](#2.1 概念及其结构)
- [2.2 定义顺序表结构](#2.2 定义顺序表结构)
- [2.3 顺序表的初始化](#2.3 顺序表的初始化)
- [2.4 顺序表的销毁](#2.4 顺序表的销毁)
- [2.5 顺序表的插入](#2.5 顺序表的插入)
- - [2.5.1 尾插](#2.5.1 尾插)
  - [2.5.2 头插](#2.5.2 头插)
- [2.6 打印](#2.6 打印)
- [2.7 顺序表的删除](#2.7 顺序表的删除)
- - [2.7.1 尾删](#2.7.1 尾删)
  - [2.7.2 头删](#2.7.2 头删)
- [2.8 指定位置之前插入/指定位置删除数据](#2.8 指定位置之前插入/指定位置删除数据)
- - [2.8.1 指定位置之前插入](#2.8.1 指定位置之前插入)
  - [2.8.2 指定位置删除](#2.8.2 指定位置删除)
- [2.9 查找](#2.9 查找)
- [2.10 所有代码](#2.10 所有代码)
[3. 练习](#3. 练习)
- [3.1 移除元素](#3.1 移除元素)
- [3.2 删除有序数组的重复项](#3.2 删除有序数组的重复项)
- [3.3 合并两个有序数组](#3.3 合并两个有序数组)
[4. 顺序表的优点与局限性](#4. 顺序表的优点与局限性)
结语

前言

在计算机科学中，数据结构是组织和存储数据的基石，而线性表作为最基本的结构之一，广泛应用于各类算法和程序中。顺序表作为线性表的一种实现方式，以其连续的存储结构和高效的随机访问特性，成为许多场景下的首选。

本文将深入探讨顺序表的核心概念、实现方法及其常见操作，包括初始化、插入、删除、查找等关键功能。同时，通过实际代码示例和典型练习（如移除元素、合并有序数组等），帮助读者掌握顺序表的应用技巧。此外，还将分析顺序表的优势与局限性，以便在实际开发中合理选择数据结构。

无论您是初学者还是希望巩固基础，本文都将为您提供清晰、系统的知识框架，助力您更好地理解和运用顺序表。

1. 线性表

线性表（linear list）是 n 个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串...

线性表在逻辑上 是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。

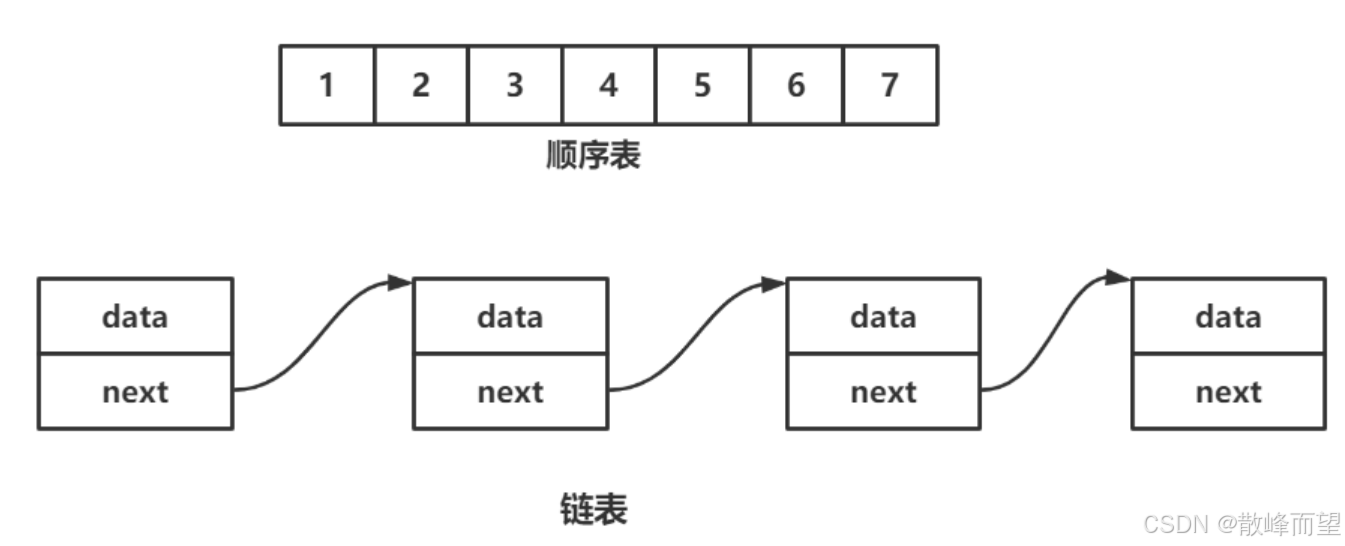
线性表中元素的个数 n（n≥0）定义称为线性表的长度，当 n = 0 时称之为空表。

对于非空的线性表，每个数据元素都有一个确定的位置，可表示为 L= (a1, a2, ..., ai - 1, ai, ai +1, ..., an)。其中，L 是表名，a1 是第一个数据元素，也称表头元素；an 是最后一个数据元素，也称表尾元素；ai - 1 处在 ai 的前边，称为 ai 的直接前驱；ai + 1 处在 ai 的后边，称为 ai 的直接后继；ai 是表中的第 i 个数据元素，也称为结点；i 是数据元素 ai 在线性表中的位序。

对于非空的线性表或线性结构，其特点是：

顺序性（序列）：元素具有线性顺序，除第一个数据元素无前驱、最后一个数据元素无后继之外，其他每个数据元素均有一个前驱和一个后继；
有限性（有限）：元素个数有限，在计算机中处理的对象都是有限的；
相同性（相同特性）：所有数据元素的类型相同，即数据元素来自于同一数据对象；
抽象性（元素类型不确定）：数据元素的类型需要根据实际的具体问题而确定，在定义中是不具体的，而是抽象的。

由抽象数据类型定义的线性表，可以根据实际所采用的存储结构形式，进行具体的

表示和实现，这里采用顺序表的形式进行实现。

2. 顺序表

2.1 概念及其结构

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。在数组上完成数据的增删查改。

顺序表的底层结构是数组，对数组的封装，实现了常用的增删查改等接口。

注意： 因为顺序表的实现采用的是数组，所以有的书、文章等可能直接写的是数组而不是线性表，但两者的本质是一样的。

由于数组存放在连续内存空间上的相同类型数据的集合，因为数组在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

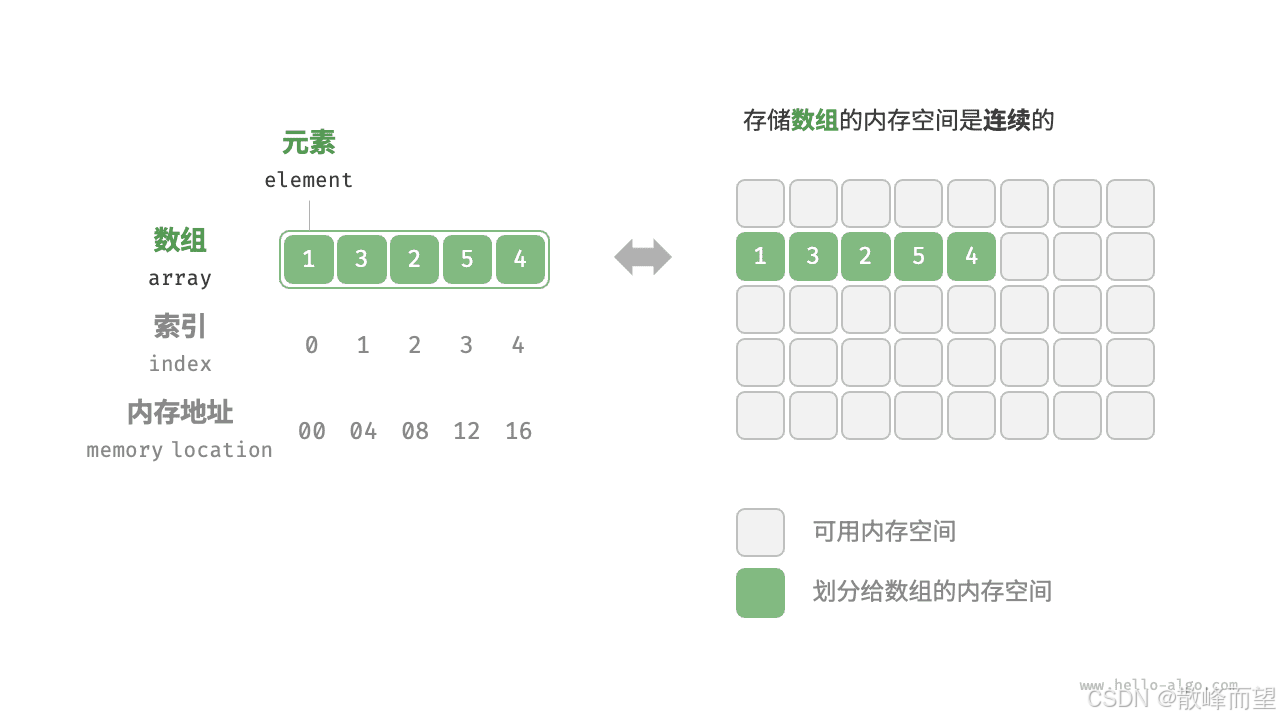
顺序表一般可以分为：

静态顺序表：使用定长数组存储元素。

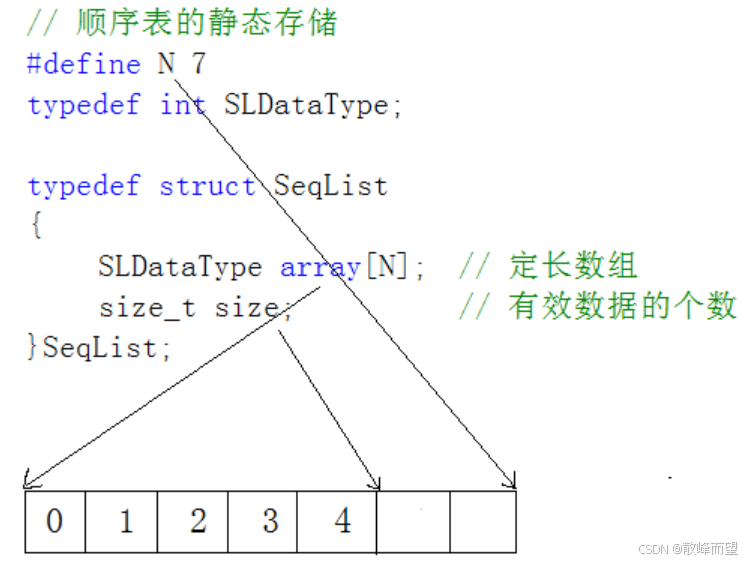
动态顺序表：使用动态开辟的数组存储。

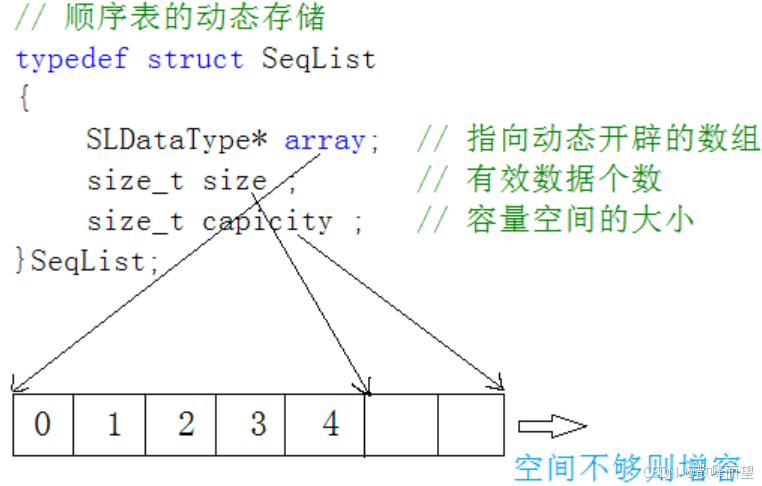
2.2 定义顺序表结构

注意：这里模拟在工程里面的使用，所以分成多个文件

创建三个文件，分别是：Seqlist.h、Seqlist.c、test.h

Seqlist.h ：顺序表结构声明顺序表的方法
Seqlist.c ：实现顺序表的方法
test.c ：测试文件

静态顺序表：

Seqlist.h

c 复制代码

#define N 100

//静态顺序表
struct SeqList
{
	int arr[N];
	int size;//有效数据个数
};

静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，空间开多了浪费，开少了不够用。所以现实中基本都是使用动态顺序表，根据需要动态的分配空间大小，所以下面我们实现动态顺序表。

动态顺序表：

Seqlist.h

c 复制代码

//动态顺序表
typedef int SLDataType;//方便后续类型的统一替换

typedef struct SeqList
{
	SLDataType* arr;
	int size;//有效数据个数
	int capacity;//空间大小
}SL;

typedef int SLDataType; 之所以这样重命名定义是为了后期有大量代码时，此时输入的不再是 int 类型，可能是 char、double 类型，方便修改。

typedef struct SeqList { }SL; 这样是为了更方便的进行调用。

2.3 顺序表的初始化

Seqlist.h 文件里先写出所需的头文件：

c 复制代码

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>

之后写出初始化的声明：

c 复制代码

//顺序表初始化
void SLInit(SL* ps);

Seqlist.c 文件写出实现文件：全部初始化为 0

c 复制代码

void SLInit(SL* ps)//传值调用会报错
{
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
	//也可以初始化就给一块空间
	//ps->arr = malloc();
	//ps->size = ps->capacity = 10;
}

void SLInit(SL s) 传值调用会报错：使用未初始化的局部变量

test.c

c 复制代码

void SLTest01()
{
    SL sl;
    SLInit(sl);
}

这是因为传实参让形参来实现，传值的本质是值的拷贝 ，而 sl 没有初始化，没有值，故要对其初始化就必须传地址。

test.c 应该为：

c 复制代码

void SLTest01()
{
    SL sl;
    SLInit(&sl);
}

2.4 顺序表的销毁

Seqlist.h 中写出销毁的声明：

c 复制代码

//顺序表的销毁
void SLDestory(SL* ps);

Seqlist.c 中写出销毁的实现：

c 复制代码

//顺序表的销毁
void SLDestory(SL* ps)
{
	if (ps->arr)//有空间就销毁
	{
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

2.5 顺序表的插入

这里讲解两种插入：头部插入 和尾部插入。也就是分别是从第一个节点插入和最后一个结点插入。

Seqlist.h 中写出声明：

c 复制代码

//尾插
void SLPushBack(SL* ps, SLDataType x);
//头插
void SLPushFront(SL* ps, SLDataType x);

SL* ps ：要往哪插
SLDataType x ：要插入的值

2.5.1 尾插

因为我们知道 size 指向的是尾节点的下一个位置，而尾插就是往尾节点的下一个位置进行插入，所以我们可以这样写

Seqlist.h

c 复制代码

//尾插-未封装函数前
void SLPushBack(SL* ps, SLDataType x)
{
	ps->arr[ps->size] = x;
	++ps->size;
	//可以合并为 ps->arr[ps->size++] = x;
}

不过这样直接尾插是有错误的，因为我们在创建时让空间的值为 0，没法进行插入，故我们需要先判断插入的空间够不够 ，如果不够就要申请空间。

要申请多大的空间呢？一次增容增多少？

增容通常是成倍数的增加，一般是 2 或 3 倍，这是数学推理出来的。

Seqlist.c

c 复制代码

//插入数据之前判断空间够不够
if (ps->capacity == ps->size)
{
	//申请空间
	//需要先判断capactity空间容量是否为0
	int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
	//ps->arr = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
	//这样直接写的话会有申请失败的问题，所以还要检查一下申请是否失败的判断
	//先放在一个临时指针
	SLDataType* tmp= (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
	if (tmp == NULL)
	{
		perror("realloc fail!");
		exit(1);
	}
	//空间申请成功
	ps->arr = tmp;
	ps->capacity = newCapacity;
}

判断空间是否充足在头插时我们也需要用到，所以我们直接封装成函数进行调用：

Seqlist.c

c 复制代码

void SLCheckCapacity(SL* ps)
{
	//插入数据之前判断空间够不够
	if (ps->capacity == ps->size)
	{
		//申请空间
		//需要先判断capactity空间容量是否为0
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		//ps->arr = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
		//这样直接写的话会有申请失败的问题，所以还要检查一下申请是否失败的判断
		//先放在一个临时指针
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);//不在main函数里面使用exit(1)，直接退出，不再继续执行
		}
		//空间申请成功
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}

之后因为可能会有传空指针的情况，所以我们需要进行判断。

test.c

c 复制代码

SLPushBack(NULL, 5);//指针为空，不能解引用，因此要对这种情况进行判断

故完整代码为：

Seqlist.c

c 复制代码

void SLPushBack(SL* ps, SLDataType x)
{
	////避免用户输入NULL判断ps 是否为空
	//if (ps == NULL)
	//{
	//	return;
	//}
	// 更简单的判断
	assert(ps);
	SLCheckCapacity(ps);//判断空间够不够
	//ps->arr[ps->size] = x;
	//++ps->size;
	ps->arr[ps->size++] = x;
}

2.5.2 头插

经过尾插的了解，这里头插就比较简单了。

因为我们知道数组的元素是不能删的，只能覆盖，所以为了防止覆盖要从后往前移动，将头结点空出来，然后数据个数要增加。

c 复制代码

void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);//判断空间够不够
	//先让顺序表的整体后移
	for (int i = ps->size; i > 0; i--)
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	ps->arr[0] = x;
	ps->size++;
}

2.6 打印

我们对顺序表进行头插和尾插后，我们就可以对这个插入的新链表进行打印测试是否正确。因为我们不需要修改顺序表，所以传值就行。

Seqlist.h

c 复制代码

//顺序表打印
void SLPrint(SL s);

Seqlist.c

c 复制代码

void SLPrint(SL s)
{
	for (int i = 0; i < s.size; i++)
	{
		printf("%d ", s.arr[i]);
	}
	printf("\n");
}

test.c

c 复制代码

void SLTest01()
{
	SL s1;
	//初始化
	SLInit(&s1);
	//增删查改
	//尾插
	SLPushBack(&s1, 1);
	SLPushBack(&s1, 2);
	SLPushBack(&s1, 3);
	SLPushBack(&s1, 4);
	//SLPushBack(NULL, 5);//指针为空，不能解引用，因此要对这种情况进行判断
	// 打印
	SLPrint(s1);

	//头插
	SLPushFront(&s1, 5);
	SLPushFront(&s1, 6);
    // 打印
	SLPrint(s1);
}

int main()
{
	SLTest01();
	return 0;
}

测试展示：

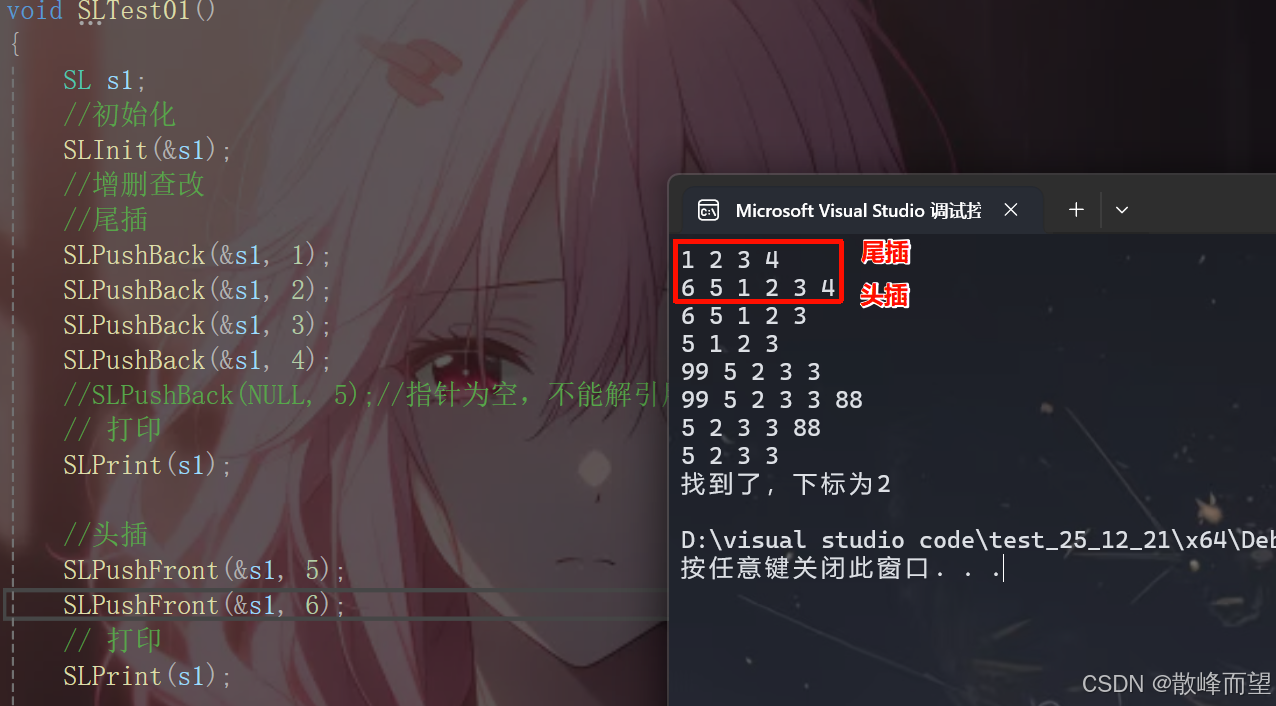
2.7 顺序表的删除

这里讲解两种分别是头部删除 和尾部删除。

Seqlist.h 中写出声明：

c 复制代码

//尾删
void SLPopBack(SL* ps);
//头删
void SLPopFront(SL* ps);

2.7.1 尾删

非常简单，只需要判断插入的不为空，且删除的顺序表不能为空，然后让数据个数减少。

Seqlist.c

c 复制代码

void SLPopBack(SL* ps)
{
	//不能为空,为空不能执行删除操作
	assert(ps);
	assert(ps->size);//顺序表不为空
	//ps->arr[ps->size - 1] = -1;//表示把这个位置的值删去，可以不要这段代码
	//因为size--完后不会访问后面的数据，如果想尾插的话会覆盖原来的值
	--ps->size;
}

2.7.2 头删

由于数组的元素是不能删的，只能覆盖，所以我们让数据从前往后覆盖，然后让数据个数减少。

Seqlist.c

c 复制代码

void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size);
	//数据整体向前移动
	for (int i = 0; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
		//arr[size - 2] = arr[size - 1]
	}
	ps->size--;
}

然后就是对这些封装的函数进行测试调用。

2.8 指定位置之前插入/指定位置删除数据

Seqlist.h 中写出声明：

c 复制代码

void SLInsert(SL* ps, int pos, SLDataType x);
void SLErase(SL* ps, int pos);

SL* ps ：要往哪插入/删除
int pos ：要插入/删除的位置
SLDataType x ：要插入的值

2.8.1 指定位置之前插入

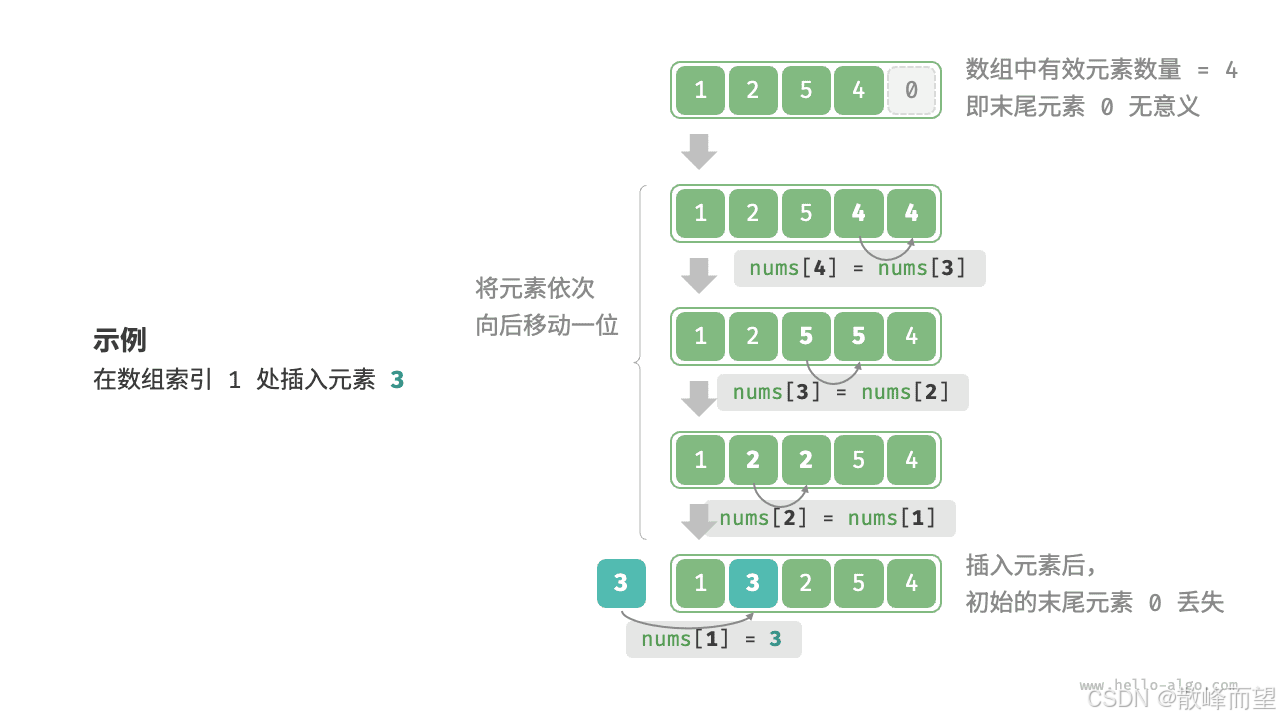
我们要注意插入的位置要大于 0 且不大于数据个数对应的下标。其他的和头插差不多，pos 之前的数据不要动，之后的数据重复头插的操作。然后在插入时要判断空间大小够不够。

Seqlist.c

c 复制代码

void SLInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);//=ps->size时相当于尾插
	//插入数据空间够不够
	SLCheckCapacity(ps);
	//让pos后面的数据往后挪，从后往前挪
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	ps->arr[pos] = x;
	ps->size++;
}

2.8.2 指定位置删除

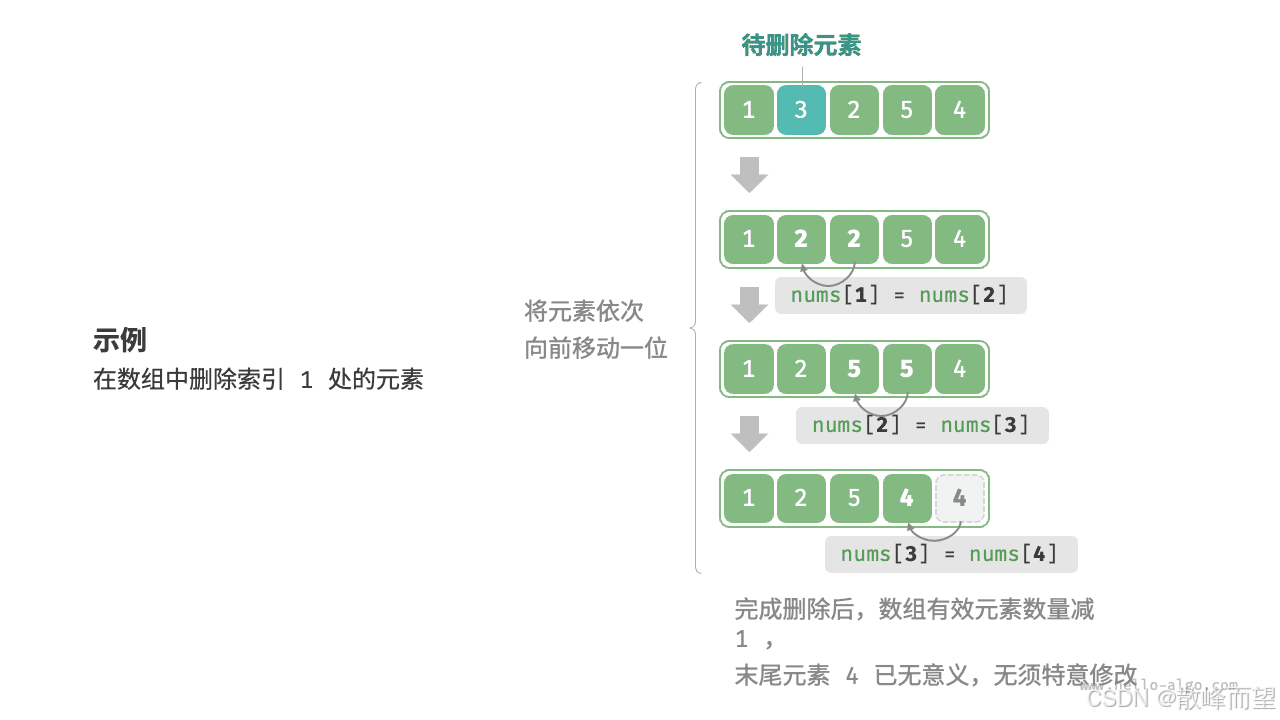
我们要注意插入的位置要大于 0 且小于数据个数对应的下标。

Seqlist.c

c 复制代码

void SLErase(SL* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);
	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
	}
	ps->size--;
}

2.9 查找

查找也很简单，只需要保证查找的值是等于我们想要的值即可。

Seqlist.c

c 复制代码

int SLFind(SL* ps, SLDataType x)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++) 
	{
		if (ps->arr[i] == x) 
		{
			//找到了
			return i;
		}
	}
	//没有找到
	return -1;
}

2.10 所有代码

Seqlist.h

c 复制代码

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
//定义顺序表结构

//#define N 100
//
////静态顺序表
//struct SeqList
//{
//	int arr[N];
//	int size;//有效数据个数
//};

//动态顺序表
typedef int SLDataType;//方便后续类型的统一替换

typedef struct SeqList
{
	SLDataType* arr;
	int size;
	int capacity;
}SL;

//顺序表初始化
//void SLInit(SL s);
void SLInit(SL* ps);

//顺序表的销毁
void SLDestory(SL* ps);

//顺序表打印
void SLPrint(SL s);//不需要改可以传值

//头部插入删除 / 尾部插入删除 
void SLPushBack(SL* ps, SLDataType x);
void SLPopBack(SL* ps);

void SLPushFront(SL* ps, SLDataType x);
void SLPopFront(SL* ps);

//指定位置之前插入/删除数据 
void SLInsert(SL* ps, int pos, SLDataType x);
void SLErase(SL* ps, int pos);

//查找
int SLFind(SL* ps, SLDataType x);

Seqlist.c

c 复制代码

#include "SeqList.h"

//1.初始化
//void SLInit(SL s)//传值调用会报错
//{
//	s.arr = NULL;
//	s.size = s.capacity = 0;
//}
void SLInit(SL* ps)//传值调用会报错
{
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
	//也可以初始化就给一块空间
	//ps->arr = malloc();
	//ps->size = ps->capacity = 10;
}

//5.由于头插和尾插都需要判断空间够不够，于是干脆设一个函数判断
void SLCheckCapacity(SL* ps)
{
	//插入数据之前判断空间够不够
	if (ps->capacity == ps->size)
	{
		//申请空间
		//需要先判断capactity空间容量是否为0
		int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		//ps->arr = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
		//这样直接写的话会有申请失败的问题，所以还要检查一下申请是否失败的判断
		//先放在一个临时指针
		SLDataType* tmp = (SLDataType*)realloc(ps->arr, newCapacity * sizeof(SLDataType));
		if (tmp == NULL)
		{
			perror("realloc fail!");
			exit(1);//不在main函数里面使用exit(1)，直接退出，不再继续执行
		}
		//空间申请成功
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
}

//3.尾插-封装函数后
//void SLPushBack(SL* ps, SLDataType x)
//{
//	//ps->arr[ps->size] = x;
//	//++ps->size;
//	ps->arr[ps->size++] = x;
//}//不全
void SLPushBack(SL* ps, SLDataType x)
{
	////避免用户输入NULL判断ps 是否为空
	//if (ps == NULL)
	//{
	//	return;
	//}
	// 更简单的判断
	assert(ps);
	SLCheckCapacity(ps);//判断空间够不够
	//ps->arr[ps->size] = x;
	//++ps->size;
	ps->arr[ps->size++] = x;
}

//4.头插
void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);//判断空间够不够
	//先让顺序表的整体后移
	for (int i = ps->size; i > 0; i--)
	{
		ps->arr[i] = ps->arr[i - 1];
	}
	ps->arr[0] = x;
	ps->size++;
}

//7.尾删
void SLPopBack(SL* ps)
{
	//不能为空,为空不能执行删除操作
	assert(ps);
	assert(ps->size);//顺序表不为空
	//ps->arr[ps->size - 1] = -1;//表示把这个位置的值删去，可以不要这段代码
	//因为size--完后不会访问后面的数据，如果想尾插的话会覆盖原来的值
	--ps->size;
}

//8.头删
void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size);
	//数据整体向前移动
	for (int i = 0; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];
		//arr[size - 2] = arr[size - 1]
	}
	ps->size--;
}

//9.指定位置之前插入数据
void SLInsert(SL* ps, int pos, SLDataType x)
{
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);//=ps->size时相当于尾插
	//插入数据空间够不够
	SLCheckCapacity(ps);
	//让pos后面的数据往后挪，从后往前挪
	for (int i = ps->size; i > pos; i--)
	{
		ps->arr[i] = ps->arr[i - 1];//arr[pos+1]=arr[pos]
	}
	ps->arr[pos] = x;
	ps->size++;
}

//10.删除指定位置的数据
void SLErase(SL* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);
	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->arr[i] = ps->arr[i + 1];//arr[size-2]=arr[size-1]
	}
	ps->size--;
}

//11.查找
int SLFind(SL* ps, SLDataType x)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++) 
	{
		if (ps->arr[i] == x) 
		{
			//找到了
			return i;
		}
	}
	//没有找到
	return -1;
}

//2.顺序表的销毁
void SLDestory(SL* ps)
{
	if (ps->arr)//有空间就销毁
	{
		free(ps->arr);
	}
	ps->arr = NULL;
	ps->size = ps->capacity = 0;
}

//6.打印
void SLPrint(SL s)
{
	for (int i = 0; i < s.size; i++)
	{
		printf("%d ", s.arr[i]);
	}
	printf("\n");
}

test.c

c 复制代码

#define _CRT_SECURE_NO_WARNINGS
#include"SeqList.h"

//初始化
//void SLTest01()
//{
//	SL s1;
//	SLinit(s1);
//}
//int main()
//{
//	SLTest01();
//	return 0;
//}//传值

void SLTest01()
{
	SL s1;
	//初始化
	SLInit(&s1);
	//增删查改
	//尾插
	SLPushBack(&s1, 1);
	SLPushBack(&s1, 2);
	SLPushBack(&s1, 3);
	SLPushBack(&s1, 4);
	//SLPushBack(NULL, 5);//指针为空，不能解引用，因此要对这种情况进行判断
	// 打印
	SLPrint(s1);

	//头插
	SLPushFront(&s1, 5);
	SLPushFront(&s1, 6);
    // 打印
	SLPrint(s1);

	//尾删
	SLPopBack(&s1);
	SLPrint(s1);

	//头删
	SLPopFront(&s1);
	SLPrint(s1);

	//指定位置之前插入
	SLInsert(& s1, 0, 99);
	SLPrint(s1);
	SLInsert(&s1, s1.size, 88);
	SLPrint(s1);

	//指定位置删去
	SLErase(&s1, 0);
	SLPrint(s1);
	SLErase(&s1, s1.size - 1);
	SLPrint(s1);

	//查找
	int find = SLFind(&s1, 3);
	if (find < 0)
	{
		printf("没有找到\n");
	}
	else
	{
		printf("找到了，下标为%d\n", find);
	}

	//销毁
	SLDestory(&s1);
}
int main()
{
	SLTest01();
	return 0;
}

还有更多的创建方法可以自行探索。

3. 练习

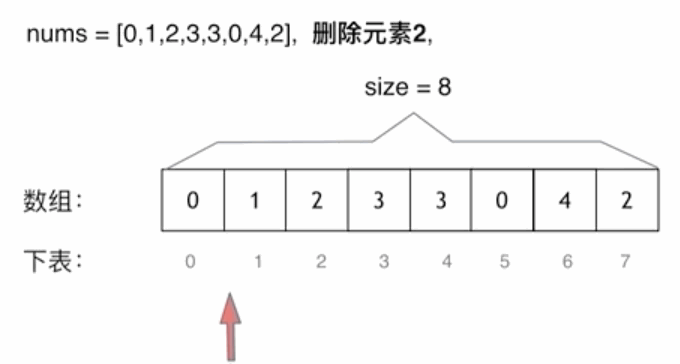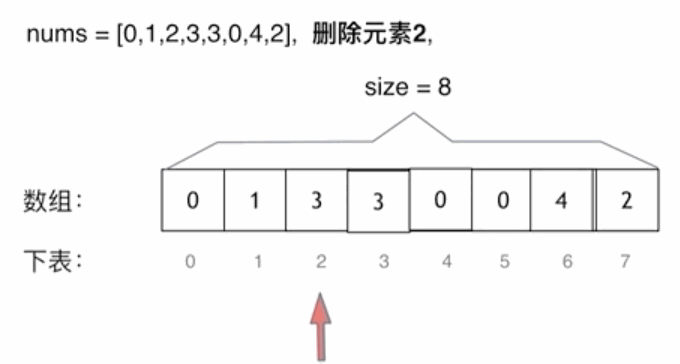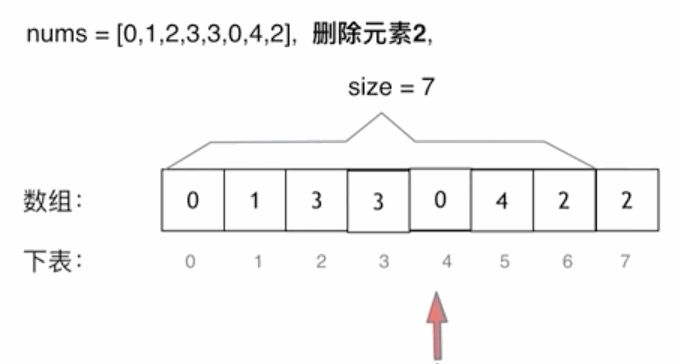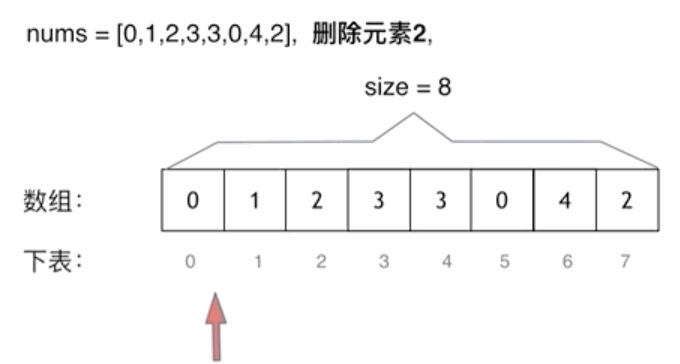
3.1 移除元素

移除元素

思路一： 两层 for 循环，一个 for 循环遍历数组元素，第二个 for 循环更新数组

c 复制代码

int removeElement(int* nums, int numsSize, int val) {
    for(int i = 0; i < numsSize; i++) {
        if(nums[i] == val) {
            for(int j = i + 1; j < numsSize; j++) {
                nums[j - 1] = nums[j];
            }
            i--;// 因为下标i以后的数值都向前移动了一位，所以i也向前移动一位
            numsSize--;
        }
    }
    return numsSize;
}

时间复杂度：O(n^2)
空间复杂度：O(1)

思路二： 创建新的数组，遍历原数组，将非 val 的值放在新数组中，原数组删去，之后再看有多少

c 复制代码

int removeElement(int* nums, int numsSize, int val) {
    // 创建临时数组
    int* temp = (int*)malloc(numsSize * sizeof(int));
    int k = 0;
    
    // 遍历原数组，将非val的元素放入临时数组
    for (int i = 0; i < numsSize; i++) {
        if (nums[i] != val) {
            temp[k] = nums[i];
            k++;
        }
    }
    
    // 将临时数组的内容复制回原数组
    for (int i = 0; i < k; i++) {
        nums[i] = temp[i];
    }
    
    free(temp);
    return k;
}

时间复杂度：O(n)
空间复杂度：O(n)

⭐思路三：快慢指针法

快慢指针法：通过一个快指针和慢指针在一个循环下完成两个循环的工作。

定义快慢指针

快指针：寻找新数组的元素，新数组就是不含有目标元素的数组
慢指针：指向更新新数组下标的位置

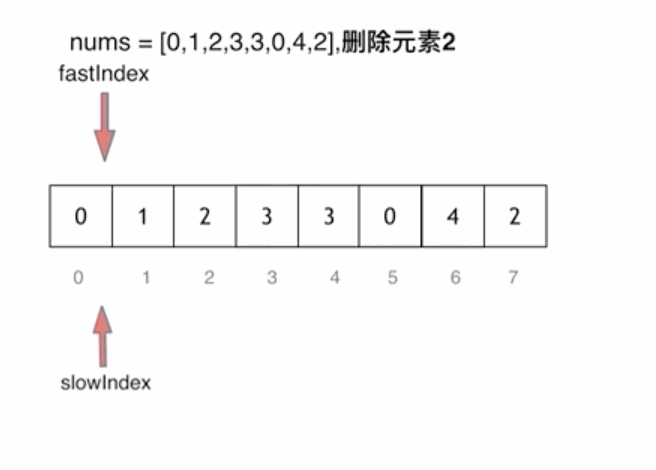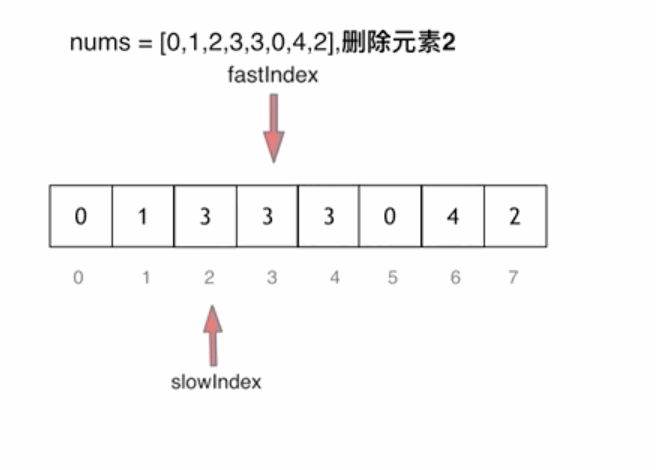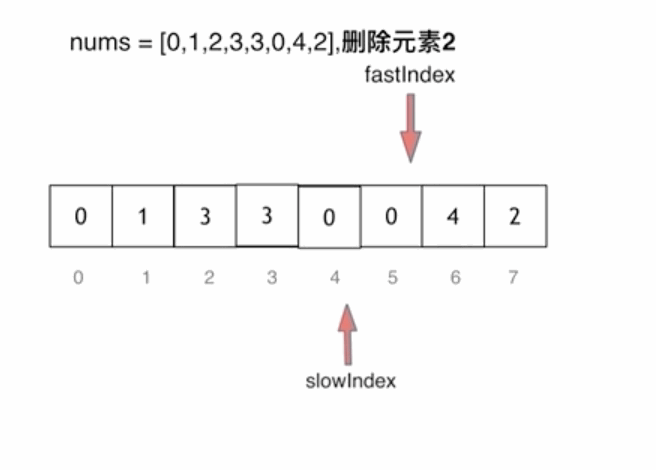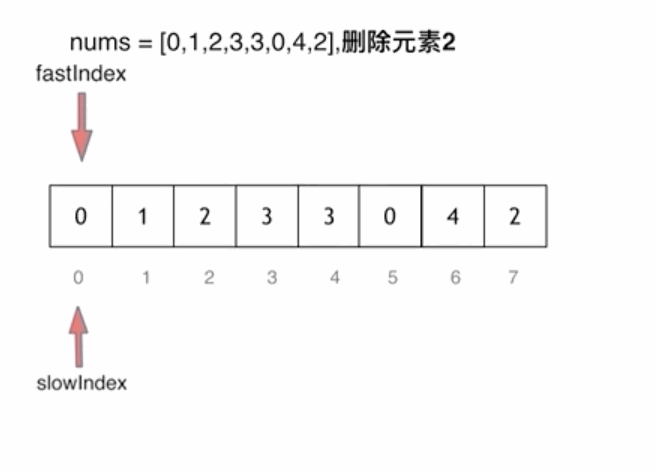
创建两个变量src，dest

（1）若 src 指向的值为 val，则 src++

（2）若 src 指向的值不是 val，则 nums[dst] = nums[src]，src++，dest++

c 复制代码

int removeElement(int* nums, int numsSize, int val) {
    //先创建两个变量
        int src, dst;
        src = dst = 0;
        while(src < numsSize)
        {
            if(nums[src] == val)
            {
                src++;
            }
            else
            {
                //赋值，两指针++
                nums[dst++] = nums[src++];
            }
        }
        //此时dst的值刚好就是新数组的有效长度
        return dst;
}

c 复制代码

int removeElement(int* nums, int numsSize, int val){
    int slow = 0;
    for(int fast = 0; fast < numsSize; fast++) {
        //若快指针位置的元素不等于要删除的元素
        if(nums[fast] != val) {
            //将其挪到慢指针指向的位置，慢指针+1
            nums[slow++] = nums[fast];
        }
    }
    //最后慢指针的大小就是新的数组的大小
    return slow;
}

时间复杂度：O(1)
空间复杂度：O(1)

3.2 删除有序数组的重复项

删除有序数组的重复项

思路一： 开创额外的数组，将不同的数组放在新数组中

思路二： 用快慢指针进行扫描

c 复制代码

int removeDuplicates(int* nums, int numsSize) {
    if(numsSize == 0) {
        return 0;
    }
    int slow = 1;
    for(int fast = 1; fast < numsSize; fast++) {
        if(nums[fast] != nums[fast - 1]) {
            nums[slow] = nums[fast];
            ++slow;
        }
    }
    return slow;
}

时间复杂度：O(1)
空间复杂度：O(1)

3.3 合并两个有序数组

合并两个有序数组

思路一： 将 num2 中所有数据依次放到 num1 数组后面，用排序算法对 num1 进行排序（借助低下的排序算法会影响到整体的运行效率）

思路二： 从后往前比大小 --- 比谁大，谁大谁放后面

有两种情况：

要复制的数组有 l1，l3 两个指针，被复制的数组有 l2 一个指针。

会出现两种种情况：

l2 先出循环
l1 先出循环，num2 中还有数据未放到 num1 中

c 复制代码

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
    int l1 = m - 1;
    int l2 = n - 1;
    int l3 = m + n - 1;

    while(l1 >= 0 && l2 >= 0)
    {
        if(nums1[l1] < nums2[l2])
        {
            nums1[l3--] = nums2[l2--];
        }
        else
        {
            nums1[l3--] = nums1[l1--];
        }
    }
    //出了循环有两种情况：l1 < 0 || l2 < 0
    //是否存在l1,l2同时小于0的情况 -- 不存在
    //只需要处理l1 < 0情况（说明l2中数据还没完全放入num1中）
    while(l2 >= 0)
    {
        nums1[l3--] = nums2[l2--];
    }
}

时间复杂度：O(m + n)
空间复杂度：O(1)

对 OJ 平台模式不熟悉的可以见该篇文章了解：
OJ 题目的做题模式和相关报错情况

4. 顺序表的优点与局限性

数组存储在连续的内存空间内，且元素类型相同。这种做法包含丰富的先验信息，系统可以利用这些信息来优化数据结构的操作效率。

空间效率高：数组为数据分配了连续的内存块，无须额外的结构开销。
支持随机访问：数组允许在时间内访问任何元素。
缓存局部性：当访问数组元素时，计算机不仅会加载它，还会缓存其周围的其他数据，从而借助高速缓存来提升后续操作的执行速度。

连续空间存储是一把双刃剑，其存在以下局限性。

插入与删除效率低：当数组中元素较多时，插入与删除操作需要移动大量的元素。
长度不可变：数组在初始化后长度就固定了，扩容数组需要将所有数据复制到新数组，开销很大。
空间浪费：如果数组分配的大小超过实际所需，那么多余的空间就被浪费了。

结语

顺序表作为线性表的一种基础实现方式，以其内存连续存储的特性在数据访问效率上展现出显著优势。通过顺序存储结构，可以高效完成随机访问、尾插尾删等操作，适合静态或低频动态数据场景。然而，其插入删除的平均时间复杂度较高，且扩容可能带来性能损耗，因此在需要频繁修改数据的场景中需权衡选择。

通过移除元素、删除有序数组重复项及合并有序数组等经典题目，能够深入理解顺序表的操作逻辑与边界条件。这些练习不仅巩固了顺序表的核心操作，也为后续学习更复杂的数据结构奠定基础。

顺序表的优缺点启示我们：在程序设计时，需根据具体需求选择数据结构。若数据规模固定且注重访问速度，顺序表是理想选择；若需频繁增删，可能需要考虑链式结构或其他动态方案。理解其特性，方能灵活运用于实际问题。

愿诸君能一起共渡重重浪，终见缛彩遥分地，繁光远缀天。