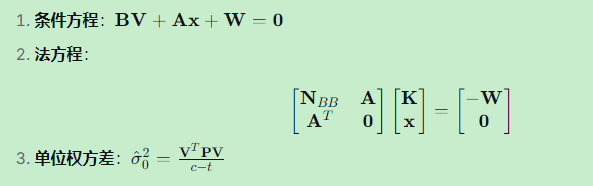附有参数的条件平差原理详解
一、基本思想与背景
附有参数的条件平差是条件平差与间接平差的结合,它解决了一类特殊的平差问题:观测值之间存在条件约束,同时又有一些未知参数需要估计。
应用场景:
-
既有几何条件约束,又有物理参数需要估计
-
条件方程中包含未知参数
-
观测值精度不等,需要统一平差
示例:
-
水准网中,既有闭合条件,又有某些点的高程作为未知参数
-
三角网中,既有三角形内角和条件,又有某些角度的系统误差参数
-
GNSS中,既有双差观测方程,又有大气延迟参数等
二、数学模型
2.1 条件方程的一般形式

2.2 线性化

三、最小二乘准则

四、拉格朗日乘数法求解
4.1 构造拉格朗日函数

4.2 求偏导并令为零
-
对 V 求偏导:

4.3 代入并整理
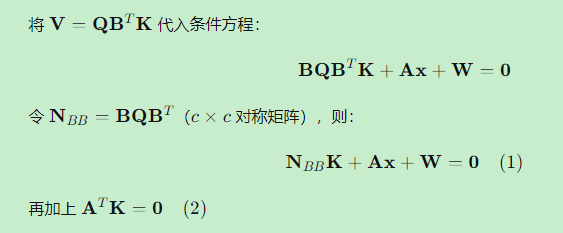
4.4 法方程

4.5 解法方程
这是一个分块矩阵方程,有多种解法:
方法一:消元法

方法二:直接求逆

4.6 计算改正数和平差值
-
参数估计值:
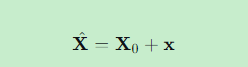
-
观测值改正数:
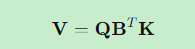
-
平差值 :
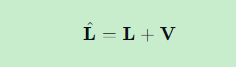
五、精度评定
5.1 单位权方差估值

5.2 参数的协因数阵

5.3 平差值 L^ 的协因数阵
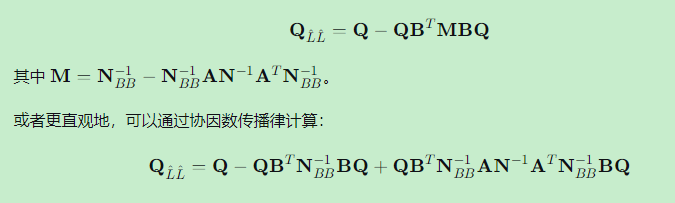
5.4 平差值函数的中误差

六、计算步骤总结
确定各类数量
七、示例:水准网附有参数的条件平差
7.1 问题描述
水准网如图,已知A点高程 H_A = 10.000mHA=10.000m,观测了3条路线的高差:
-
路线1:A→B,观测高差 h_1 = +2.500mh1=+2.500m,路线长 S_1 = 2kmS1=2km
-
路线2:B→C,观测高差 h_2 = +1.000mh2=+1.000m,路线长 S_2 = 1kmS2=1km
-
路线3:A→C,观测高差 h_3 = +3.498mh3=+3.498m,路线长 S_3 = 3kmS3=3km
附加要求:将B点高程作为未知参数进行平差。
7.2 平差计算
步骤1:确定数量
模型1(传统条件平差):
模型2(附有参数的条件平差):
步骤2:线性化 
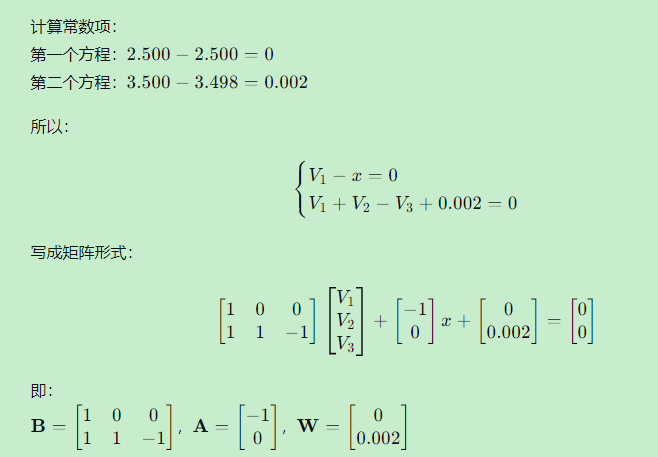
步骤3:定权 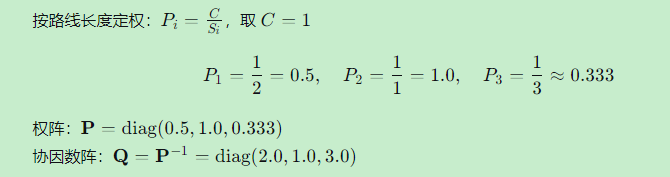
步骤4:组成法方程 
步骤5:解法方程 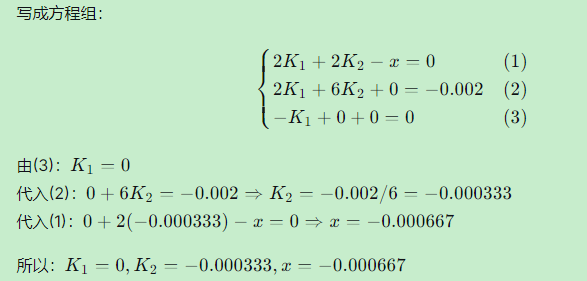
步骤6:计算改正数和平差值 
步骤7:精度评定 
八、与其它平差方法的比较
| 平差方法 | 未知数 | 方程类型 | 适用情况 |
|---|---|---|---|
| 条件平差 | 改正数V | 条件方程 | 观测值间有明显几何条件 |
| 间接平差 | 参数X | 观测方程 | 参数有明确物理意义 |
| 附有参数的条件平差 | 改正数V+参数X | 附参数的条件方程 | 既有条件约束,又有参数需要估计 |
| 附有条件的间接平差 | 参数X | 观测方程+约束条件 | 参数有约束条件 |
关系:
-
附有参数的条件平差可以转化为间接平差
-
当参数个数等于必要观测数时,附有参数的条件平差退化为间接平差
-
当没有参数时,退化为条件平差
九、在AGNSS中的应用
在GNSS数据处理中,附有参数的条件平差有重要应用:
9.1 系统间偏差估计
在多系统GNSS组合定位中,不同系统间存在时间偏差、频率偏差等,这些可以作为参数引入到条件方程中。

9.2 大气延迟参数估计
在精密单点定位(PPP)或网络RTK中,大气延迟(电离层、对流层)可以作为参数估计。

9.3 整周模糊度条件
在载波相位相对定位中,整周模糊度应满足整数条件,这可以看作是一种特殊的参数条件。
十、总结
10.1 附有参数的条件平差特点
-
结合性:结合了条件平差和间接平差的优点
-
灵活性:可以处理既有条件约束又有参数估计的复杂问题
-
统一性:是更一般的平差方法,条件平差和间接平差是其特例
10.2 关键公式
10.3 实际应用价值
-
处理复杂模型:能够处理观测方程非线性、参数有约束的问题
-
提高解算效率:对于某些问题,比间接平差方程数少
-
理论完备:为理解更复杂的平差方法(如序贯平差、卡尔曼滤波)奠定基础
掌握附有参数的条件平差原理,有助于深入理解测量平差的理论体系,并为解决复杂的GNSS数据处理问题提供有力的工具。
下面是学习笔记: