【优选算法】双指针法：移动0，复写0，快乐数，盛水最多的容器，有效三角形个数，二三四数之和

文章目录

• [1. 移动0（LC283）](#1. 移动0（LC283）)
• • 题目描述
  • 解题思路
  • 代码实现
• [2. 复写0（LC1089）](#2. 复写0（LC1089）)
• • 题目描述
  • 解题思路
  • 代码实现
• [3. 快乐数（LC202）](#3. 快乐数（LC202）)
• • 题目描述
  • 解题思路
  • 代码实现
• [4. 盛水最多的容器（LC11）](#4. 盛水最多的容器（LC11）)
• • 题目描述
  • 解题思路
  • 代码实现
• [5. 有效三角形个数（LC611）](#5. 有效三角形个数（LC611）)
• • 题目描述
  • 解题思路
  • 代码实现
• [6. 查找总价格为目标值的两个商品（LCR 179）](#6. 查找总价格为目标值的两个商品（LCR 179）)
• • 题目描述
  • 解题思路
  • 代码实现
• [7. 三数之和（LC15）](#7. 三数之和（LC15）)
• • 题目描述
  • 解题思路
  • 代码实现
• [8. 四数之和（LC18）](#8. 四数之和（LC18）)
• • 题目描述
  • 解题思路
  • 代码实现

1. 移动0（LC283）

移动0

题目描述

解题思路

这类题可以归类为数组划分 或数组分块。特点：指定一个标准，把数组分成若干个区间。

1. 定义两个指针dest和cur,数组被分为三个区域

   • cur从左往右扫描数组
   • dest表示已处理区间内非0元素最后一个位置
     

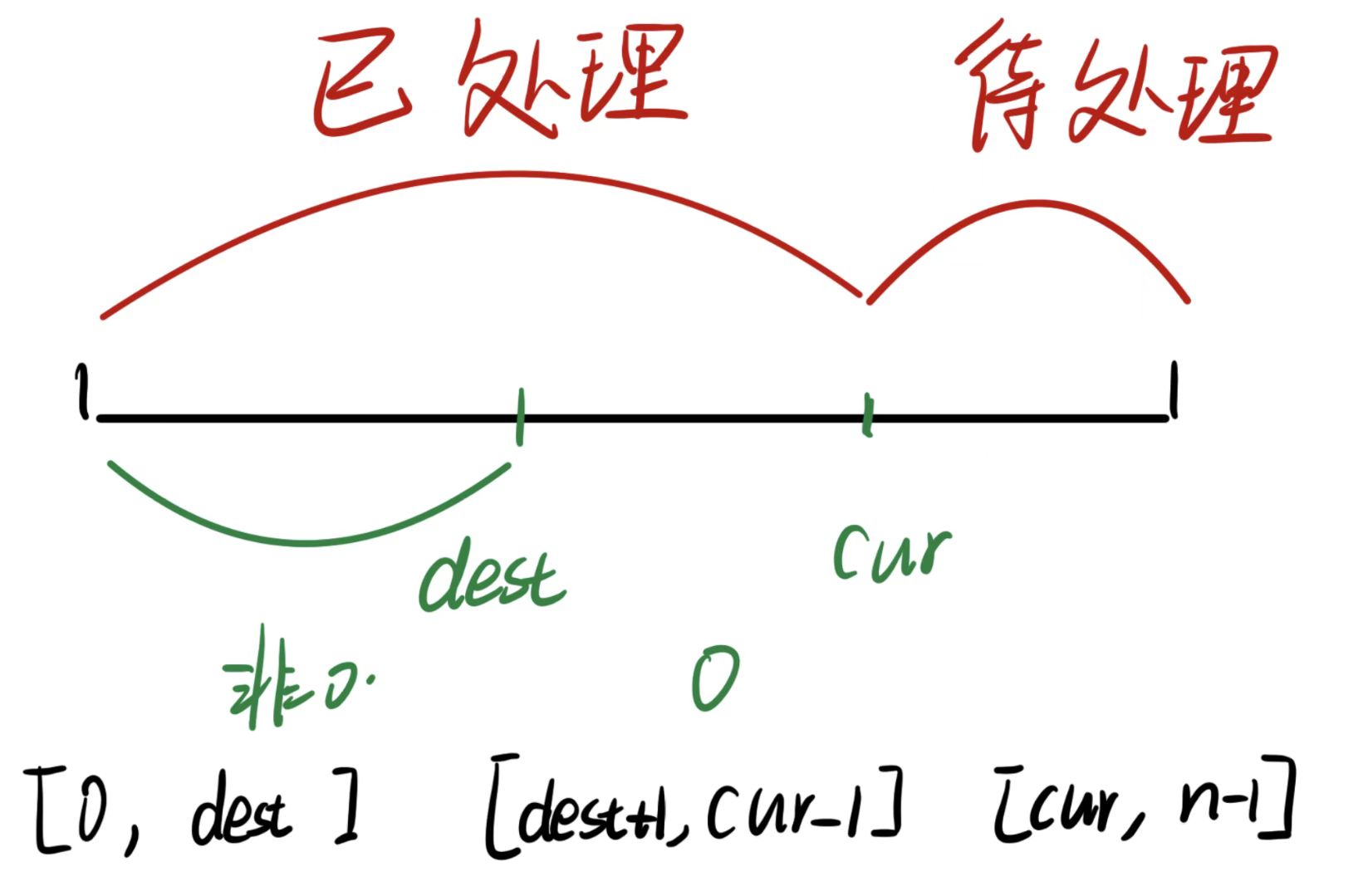
2. cur从左往右扫描过程中：

   • 如果遇到0：要保证整个数组是[非0区域，0区域，待处理元素]，所以遇到0不需要做任何操作，只需要让cur++;
   • 遇到非0：dest表示非零元素的最后一个，所以先让dest++，cur与dest位置交换元素，cur++

扩展： 快速排序中的核心思想是选定基准值，把数组划分为两部分，左半部分小于基准值，右半部分大于基准值，与这里的双指针法的思想类似。

代码实现

    public void moveZeroes(int[] nums) {
        for(int cur=0,dest=-1;cur<nums.length;cur++){
            if(nums[cur]!=0){
                dest++;
                int tmp = nums[dest];
                nums[dest]=nums[cur];
                nums[cur]=tmp;
            }
        }
    }

注意： 不可以把cur位置元素赋值给dest位置元素，再把cur位置元素赋值为0。当测试用例为[1]时，会把1改为0。必须写成交换的形式。

2. 复写0（LC1089）

覆写0

题目描述

解题思路

1. 先在两个数组上通过两个指针，cur指向原数组，dest指向结果数组，进行复写过程，再转换到原数组上模拟复写过程。通过测试发现从左往右复写是行不通的，由于dest比cur走得快，会覆盖掉还没有复写的数字，因此转变策略，从右往左进行复写

2. 先找到结果数组中最后一个需要复写的数字

   1. cur从左向右扫描数组，令cur初始化为0；dest表示结果数组中最后的位置，因此dest初始化为-1。
   2. 先判断cur位置的值，决定dest向后走一步还是走两步
   3. 判断dest是否走到结尾，如果走到结尾直接退出循环
   4. cur++

3. 从右向左完成复写操作

注意： 特殊的测试用例：如果cur最后指向0，导致dest越界，需要处理边界情况 。

由于dest已经越界，只需要把dest-1位置修改为0，再让dest向前移动两步，cur向前走一步。接下来完成复写操作。

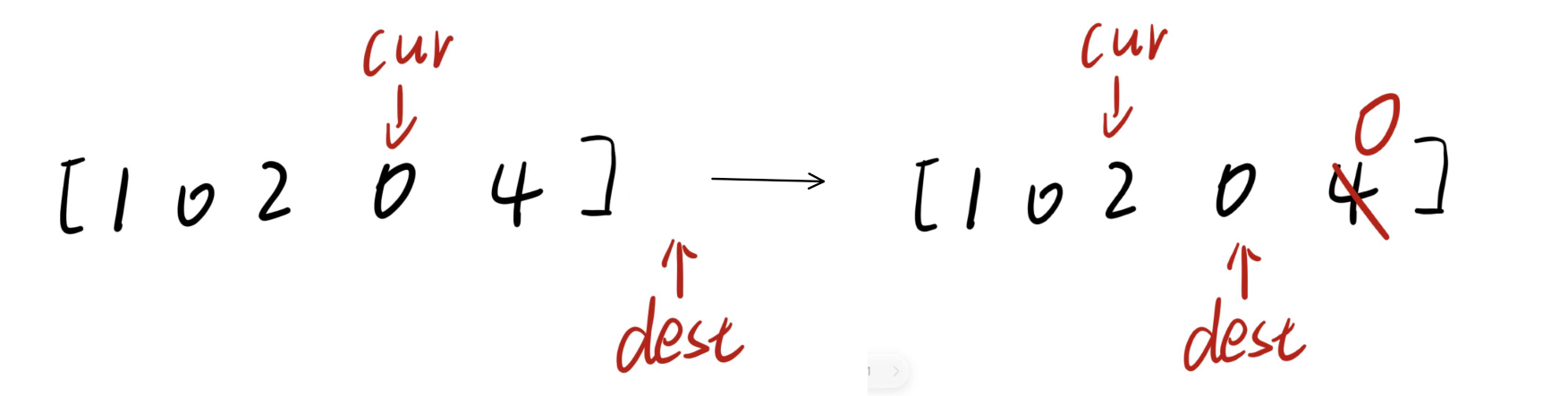
代码实现

public void duplicateZeros(int[] arr) {
        int cur = 0;
        int dest = -1;
        int n = arr.length;

        //找到最后一个复写的数字
        while (cur < n) {
            if (arr[cur] == 0)
                dest += 2;
            else
                dest++;
            //dest到结尾就直接退出循环
            if (dest >= n - 1) 
                break;
            cur++;
        }
        //处理越界情况
        if(dest==n){
            arr[dest - 1] = 0;
            dest -= 2;
            cur--;
        }
        //从右向左进行复写
        while (cur >= 0 && dest >= 0) {
            if (arr[cur] == 0) {
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            } else {
                arr[dest--] = arr[cur--];
            }
        }
    }

3. 快乐数（LC202）

快乐数

题目描述

解题思路

分为两种情况：一种是结果为1，另一种是结果成环。第一种情况也可以抽象理解为环里的数字都为1。类似于判断链表是否存在环，采用快慢指针方法。（这里指针只是一种思想，落到这个题里面是指两个整型变量.）

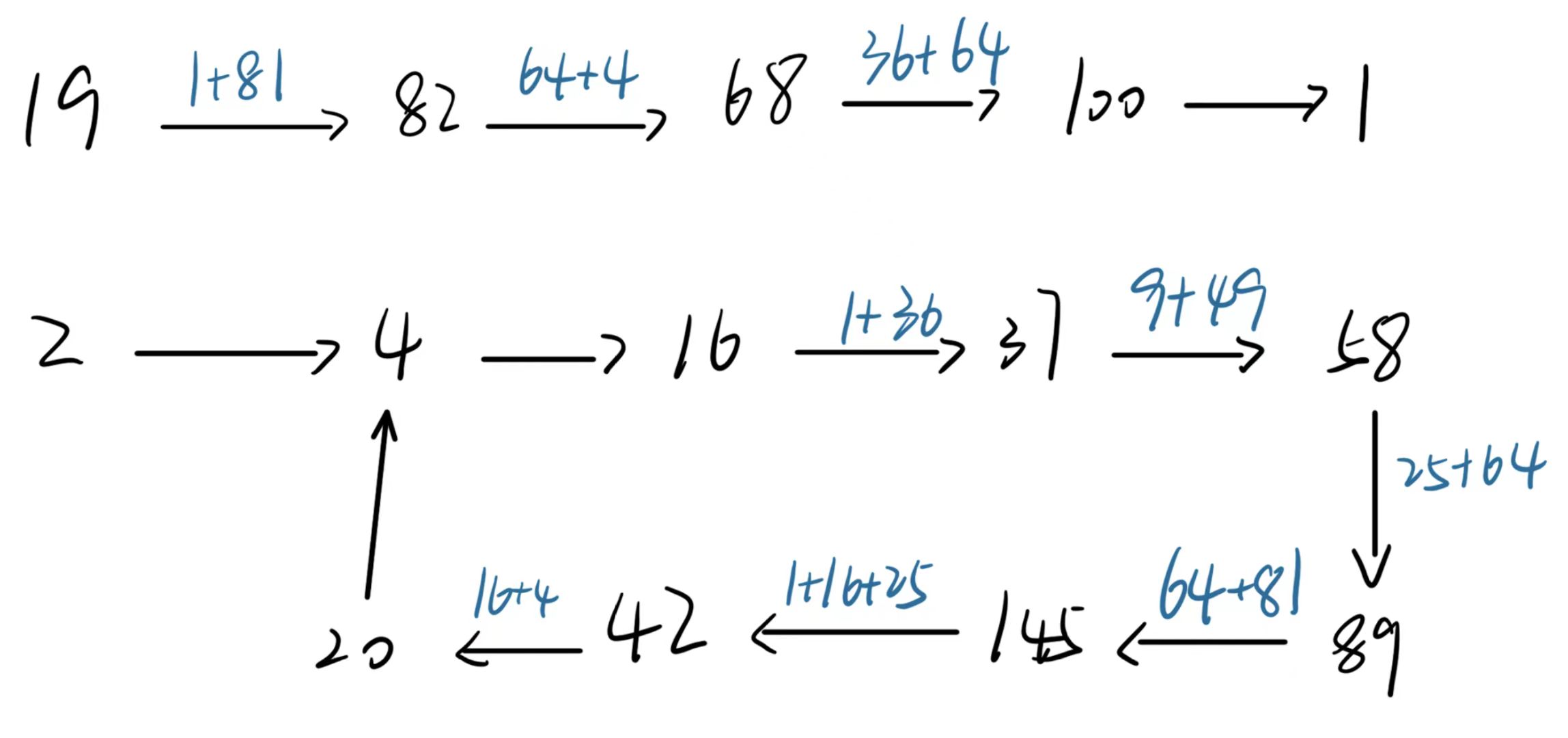
定义快指针fast和慢指针slow，快指针每次走两步，慢指针每次走一步，由于两种情况都存在环，只需要判断相遇时平方和是否为1。

代码实现

//求每一位的平方和
    int sum(int n){
        int sum = 0;
        while(n!=0){
            int tmp = n%10;
            sum += tmp*tmp;
            n/=10;
        }
        return sum;
    }

    public boolean isHappy(int n) {
        int slow = n;
        int fast = n;
        do{
            slow=sum(slow);
            fast=sum(sum(fast));
        }while(fast !=slow);
        return fast==1;
    }

4. 盛水最多的容器（LC11）

盛水最多的容器

题目描述

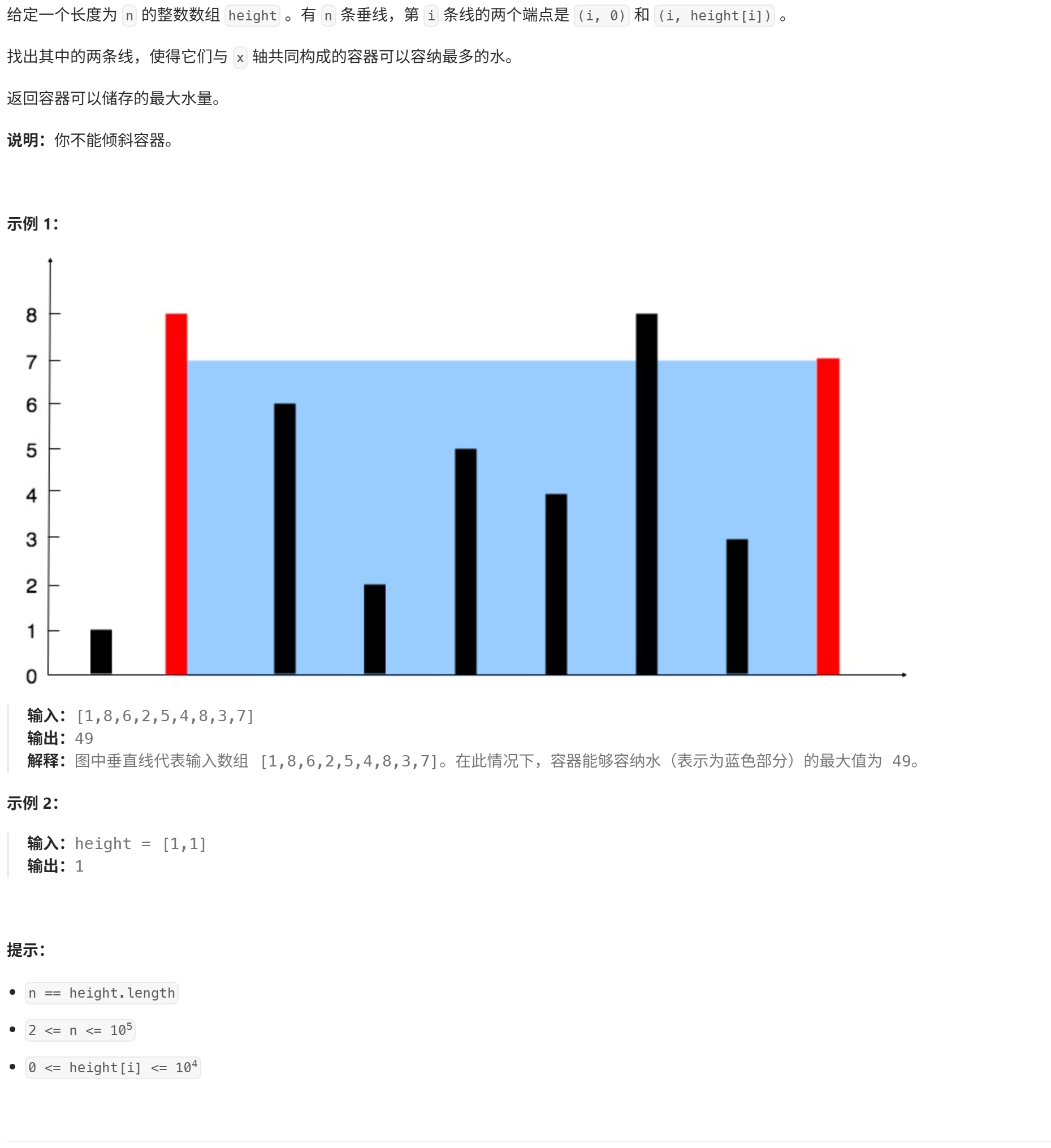
解题思路

• 思路一（暴力解法）：两层for循环，固定左端，依次枚举右端，找到最大值。时间复杂度：O（n²）
• 思路二： 利用单调性，一个指针指向数组头，一个指向尾，逐渐缩小区间。时间复杂度：O（n）
  • 当固定一端，另一端向内枚举，遇到比固定端小的值，宽度减小，高度减小，体积一定减小。因此不需要把较小值固定继续枚举。
  • 每次固定较大值，当遇到比固定端更大值时，由于木桶效应，高度不变，宽度减小，体积减小。也不需要继续枚举。
  • 每次只需要固定较大值的一端，另一端向内移动一步。每一次记录计算得到的体积，最后返回最大值。

代码实现

public int maxArea(int[] height) {
        int left = 0;
        int right = height.length -1;
        int ret = 0;
        while(left<right){
            int v = (right - left)*Math.min(height[left] , height[right]);
            ret = Math.max(ret,v);
            if(height[left]<height[right])
                left++;
            else
                right--;
        }
        return ret;
    }

5. 有效三角形个数（LC611）

有效三角形个数

题目描述

解题思路

对数组排序，利用单调性，使用双指针法来解。时间复杂度：O（n²）

1. 先固定最大的数（指针c），在最大数的左侧区间，快速统计符合的三元组
   • 如果left 和right相加大于c，那么如果固定right不变，left向右移动，与right和c组成的三元组都符合条件，此时不需要继续枚举，直接统计个数；接着让right向左移动一步
   • 如果left和right相加小于c，那么如果固定left不变，right向左移动，与left和c组成的三元组都不可能符合条件，不需要统计；接着让left向右移动一步。
   • 直到left和right相遇。固定c的一轮遍历结束
2. c向左移动一位，重复上述过程。

代码实现

public int triangleNumber(int[] nums) {
        Arrays.sort(nums);
        int n = nums.length;
        int c = n - 1;
        int count = 0;

        while(c >= 2){
            int left = 0;
            int right = c - 1;
            while(left<right){
                if(nums[left]+nums[right]>nums[c]){
                    count += right - left;
                    right --;
                }else
                    left ++;
            }
            c--;
        }
        return count;
    }

6. 查找总价格为目标值的两个商品（LCR 179）

查找总价格为目标值的两个商品

题目描述

解题思路

与上一个题类似，采用双指针法，left初始在数组头，right初始在数组尾

• 当left与right之和大于target，让right向左移动一步
• 如果小于target，left向右移动一步
• 如果相等跳出循环

代码实现

    public int[] twoSum(int[] price, int target) {
        int[] ret = new int[2];
        int left = 0;
        int right = price.length-1;

        while(left<right){
            if(price[left]+price[right]>target)
                right--;
            else if(price[left]+price[right]<target)
                left++;
            else
                break;
        }
        ret[0]=price[left];
        ret[1]=price[right];
        return ret;
    }

7. 三数之和（LC15）

三数之和

题目描述

解题思路

• 思路一： 排序+暴力枚举+set去重

• 思路二：排序+双指针法 先固定一个数，在剩下的区域内找和为固定值的相反数的组合，与上一题类似。

  • 进行一轮循环后，每遇到与上一个相同的数，移动对应下标，直到相邻两数不同，实现达到去重。
  • 优化点：由于是从0下标开始固定，找到的和一定是正数，才可以与负数相加得到0，当k对应值为正数，则不可能再找到正确的三元组，直接跳出循环。

代码实现

public List<List<Integer>> threeSum(int[] nums) {
        int k = 0;
        List<List<Integer>> ret = new ArrayList<>();

        //排序
        Arrays.sort(nums);

        while (k < nums.length - 2) {
             if(nums[k]>0)
                break;

            int target = -nums[k];
            int i = k + 1;
            int j = nums.length - 1;

            while (i < j) {
                int sum = nums[i] + nums[j];
                if (sum < target)
                    i++;
                else if (sum > target)
                    j--;
                else {
                    ret.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[j],nums[k])));
                    i++;
                    j--;
                    //去重操作
                    while(i<j && nums[i]==nums[i-1])
                        i++;
                    while(i<j && nums[j]==nums[j+1])
                        j--;
                }
            }
            //去重操作
           do k++;
           while (k < nums.length - 2 && nums[k] == nums[k - 1]);
        }
        return ret;
    }

8. 四数之和（LC18）

四数之和

题目描述

解题思路

• 思路一：排序+暴力枚举+set去重
• 思路二：排序+双指针 照搬上题思路
  依次固定一个数a， 在剩下区间内，利用三数之和的思想，求出target-a.

代码实现

public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> ret = new ArrayList<>();
        Arrays.sort(nums);
        int a = 0;
        int n = nums.length;

        while (a < n - 3) {
            int b = a + 1;

            //三数之和
            while (b < n - 2) {

                int l = b + 1;
                int r = n - 1;
                //防止溢出
                long target1 = (long)target - nums[a] - nums[b];

                while (l < r) {
                    int sum = nums[l] + nums[r];
                    if (sum > target1)
                        r--;
                    else if (sum < target1)
                        l++;
                    else {
                        ret.add(Arrays.asList(nums[a], nums[b], nums[l], nums[r]));
                        l++;
                        r--;
                        //去重
                        while (l < r && nums[l] == nums[l - 1])
                            l++;
                        while (l < r && nums[r] == nums[r + 1])
                            r--;
                    }
                }
                //去重
                do
                    b++;
                while (b < n - 2 && nums[b] == nums[b - 1]);
            }
            //去重
            do
                a++;
            while (a < n - 3 && nums[a] == nums[a - 1]);
        }

        return ret;
    }