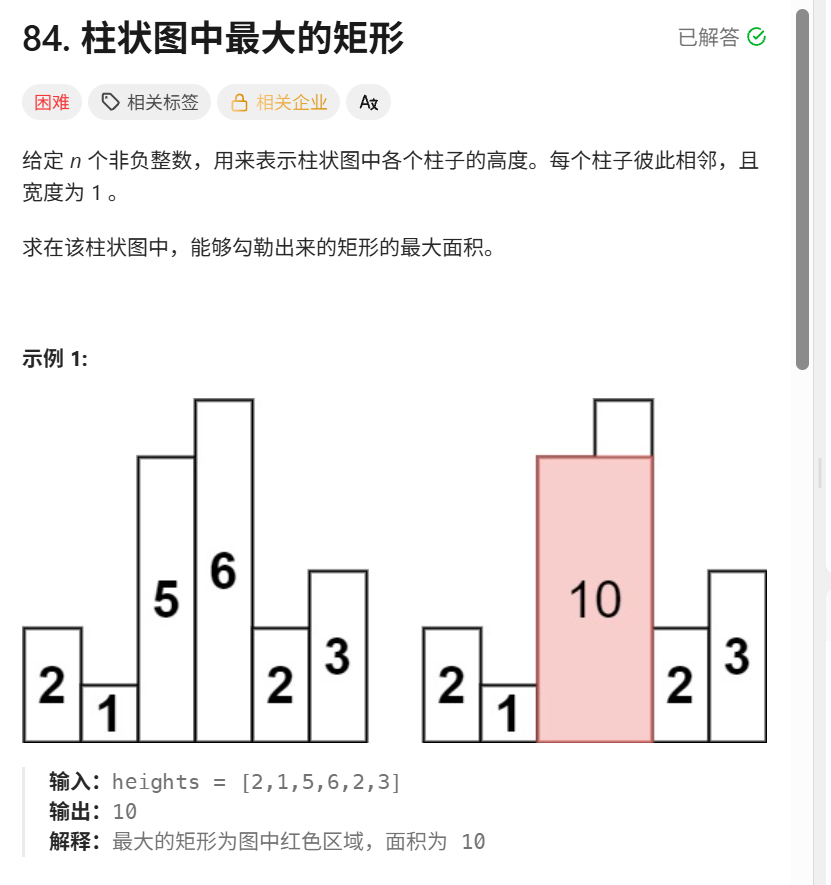
这道题有俩个难点 这个最大矩形的高是多少 矩形的宽是多少
矩形的高是多少
对于这个问题有个非常重要的结论: 最大的矩形它的高一定是以heights中的某一个高度为高的
也就是说一定是再heights[i] 中
那么我们矩形的高就确定了,这时就可以遍历所有的高,然后找到这个高它能构成的最大的矩形的宽,这样就能找到以当前高为高的矩形的最大面积,再遍历完之后,就能找到最大的矩形面积了
矩形的宽是多少
在确定高之后,由矩形的定义就知道,它左右的高度一定是相同的,那么对应到题目中就是i位置的高它左边和右边的高度都必须大于或者等于它,如果小于,就说明找到了边界了,所以对于边就可以以i为起点 左右遍历找比heights[i]小的下标 这样就找打到了宽了
到这里就已经解决了这道题
不过还可以优化下找宽的这一过程,因为我们在从左向右边遍历高度时,发现如果height[i - 1] > hrights[1] 那不就说明我i - 1 的右边界不久找到了嘛,那如果我在这时在退回去找左边界,不久优化了找右边界的情况了嘛,之后找左边界,如果我把左边的高度按升序排序,那么对于 i - 2的位置不久小于了 i - 1 那么不久找到了左边界嘛,那这样就又把找左边界给优化了
这时就发现了对于 刚刚放进去的i - 1位置下标,会在把它拿出来计算最大面积,并且还会涉及到拿出 i - 2 下标来计算左边界,而我i - 1的在计算过了最大面积之后会把它删除,这时 i - 2的其实就是新的尾巴了 ,这种后进先出的模式,就是栈了,于是可以使用一个单调的栈来优化找边的问题
并且这个栈不需要特别维护它的升序,因为每当碰到比栈顶元素小的高,那就会涉及到计算栈顶元素的最大面积,并且会弹出这个元素
细节
等到遍历完了高度之后,栈中还有元素,那就说明栈中所有元素都没有找到右边界,那么右边界的位置就应该是到 heights.length 这里,到了最后一个元素
并且如果栈弹空了,这意味着左边所有高度都比当前高,左边界应该是 -1
ac代码
java
public int largestRectangleArea(int[] heights) {
int len = heights.length;
if (len == 1) {
return heights[0];
}
// 有一个定理,就是最大矩形面积的高度一定是某个height[i]
// 储存的是一个递增的高度的下标 在这个栈中,i - 1 小于 i 如果 i + 1 小于了i 那么对于i高度的最大面积就能得到了
// 所以使用栈来存储下标
Deque<Integer> stack = new ArrayDeque<>();
int ans = 0;
for (int i = 0; i < len; i++) {
// 如果当前高度小于前一个高度,说明i-1高度的右边宽度可以确定了 所以可以得出i-1为高度的最大面积
while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
int height = heights[stack.pop()];
while (!stack.isEmpty() && height == heights[stack.peek()]) {
stack.pop();
}
int width = i - (stack.isEmpty() ? -1 : stack.peek()) - 1;
ans = Math.max(width * height, ans);
}
stack.push(i);
}
//这里剩下的是,没有比他矮的有边界的高度的下标 所以他的右边是没有比它矮的在阻挡着他,所以右边下标是在len这里的
while (!stack.isEmpty()) {
int height = heights[stack.pop()];
while (!stack.isEmpty() && height == heights[stack.peek()]) {
stack.pop();
}
int width;
// 为空是,说明i位置高度 它左边没有比他矮的挡着它,右边也没有比他矮的 所以就可以宽度为len
width = len - (stack.isEmpty() ? -1 : stack.peek()) - 1;
ans = Math.max(width * height, ans);
}
return ans;
}