DDMA MIMO OFDM ISAC：从回波模型到距离-速度图与非相参积累的原理梳理

毫米波 ISAC（通信与感知一体化）里，OFDM 波形天然具备"频域子载波 + 慢时间符号序列"的二维结构：

子载波维携带"距离（时延）"信息
符号维（慢时间） 携带"速度（多普勒）"信息

当把多天线 MIMO 引入后，还需要让不同发射通道在接收端可分离。这里采用的是 DDMA（Doppler Division Multiple Access / Doppler Division Multiplexing） 思想：通过在慢时间上施加不同的相位坡度，让不同发射天线的回波在多普勒维上"分槽"，从而实现 MIMO 复用。

本文用一个典型的 DDMA MIMO-OFDM 雷达感知链路，解释如何得到两类可视化结果：

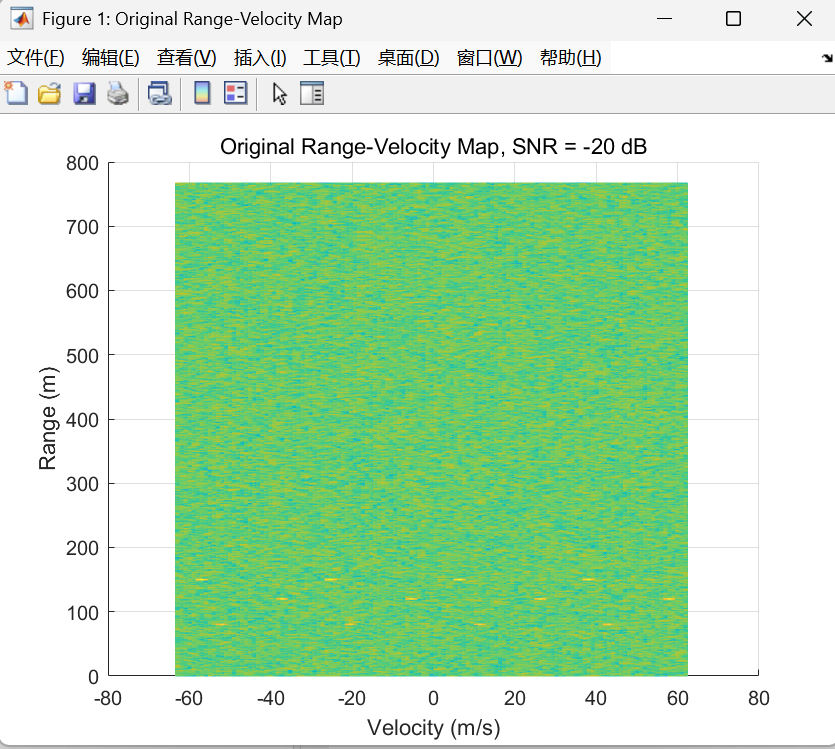
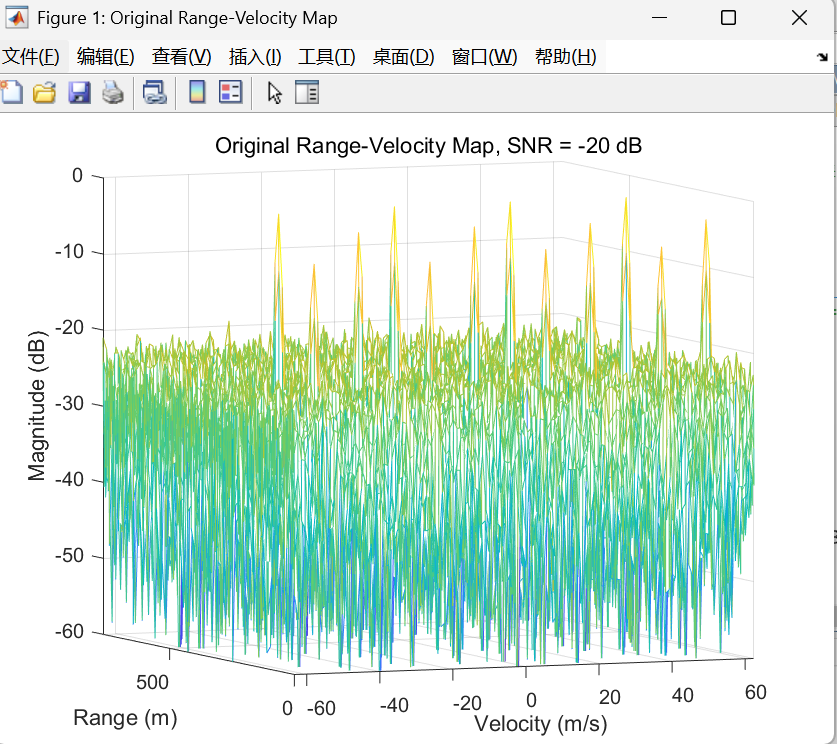
原始距离-速度图（Range-Velocity Map, RV Map）
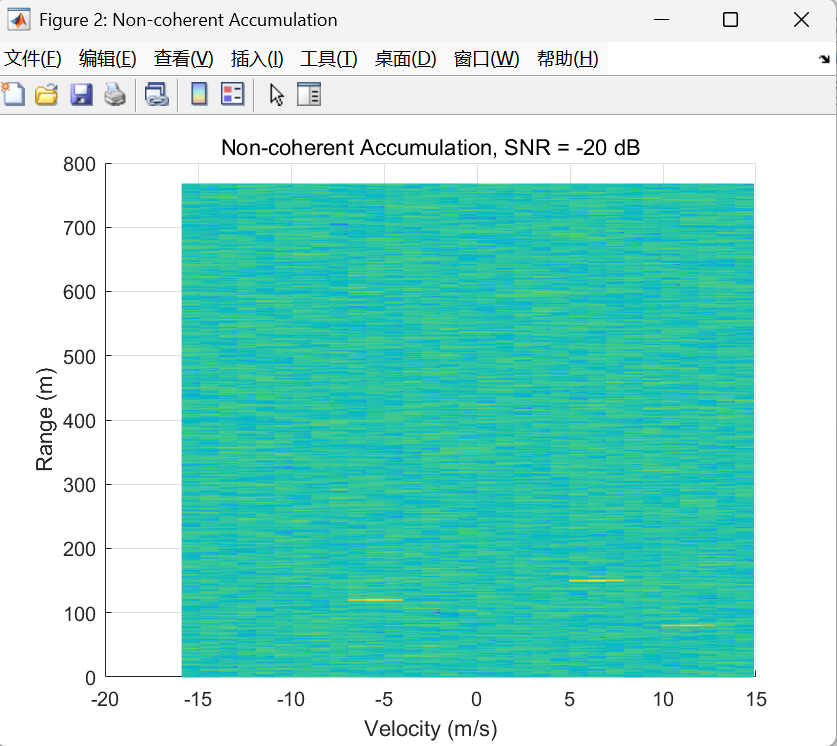
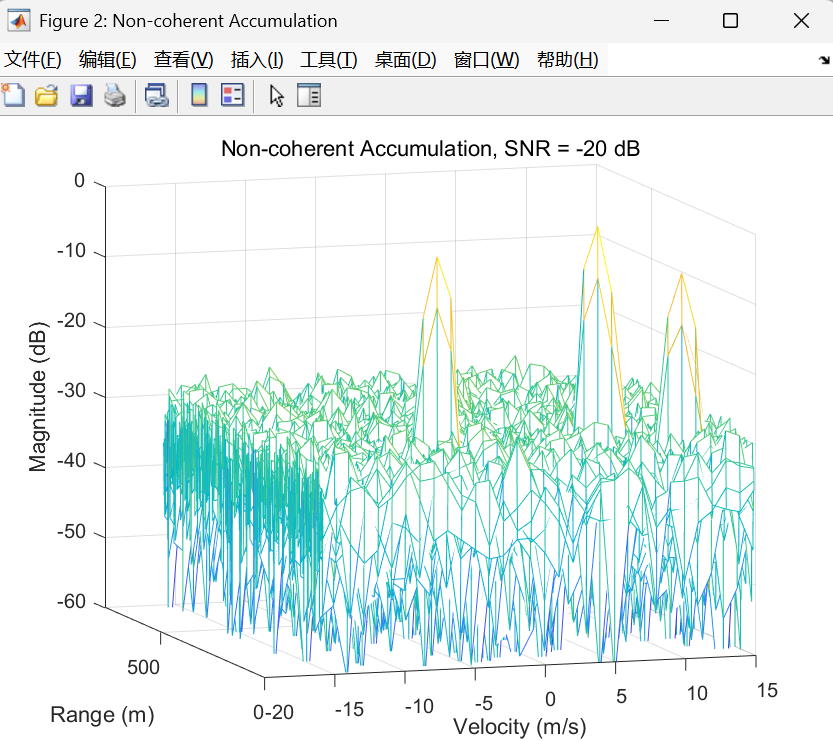
非相参积累后的输出图（把 DDMA 的多个多普勒"子带"合并以增强检测）

1. OFDM 的二维"测距 + 测速"机制

1.1 子载波相位与时延（距离）

对于单个目标，往返传播引入时延 τ=2r/c\tau = 2r/cτ=2r/c。在 OFDM 中，时延在频域表现为对子载波的线性相位：

H(n)∝e−j2πnΔfτ H(n) \propto e^{-j2\pi n\Delta f \tau} H(n)∝e−j2πnΔfτ

因此，对子载波维做 逆 FFT（IFFT） 即可把这种线性相位"聚焦"为距离域的峰值，得到距离像（range profile）。距离分辨率由带宽决定：

Δr=c2B \Delta r = \frac{c}{2B} Δr=2Bc

1.2 符号间相位与多普勒（速度）

目标速度 vvv 产生多普勒频移 fd=2vfccf_d = \frac{2v f_c}{c}fd=c2vfc。在慢时间（OFDM 符号序列）上表现为相位随符号索引 mmm 的线性累积：
ej2πfdmTsym e^{j2\pi f_d m T_\text{sym}} ej2πfdmTsym

因此，对慢时间维做FFT即可得到多普勒谱，从而估计速度。速度分辨率与 CPI 时长相关（符号数越多、符号周期越长，速度分辨率越高）。

2. DDMA：用"慢时间相位坡度"把多发射通道分开

在 DDMA MIMO-OFDM 中，不同发射天线并不使用正交码或不同频带，而是对每个发射通道施加一个固定的"跨符号相位增量"：

xq(m)∼ejmφq x_q(m) \sim e^{jm\varphi_q} xq(m)∼ejmφq

其中 qqq 表示第 qqq 个发射天线，φq\varphi_qφq 是该通道对应的 DDMA 相位步进。

直观理解：

对慢时间施加线性相位，相当于给该发射通道"人为引入一个额外的多普勒偏移"。于是同一个物理目标，在不同 Tx 通道对应的处理结果中，会出现在不同的多普勒位置（或形成周期性复制的峰值），从而实现通道分离/可区分。

3. 目标回波模型：时延 + 多普勒 + 多通道叠加

对每个目标，回波可以理解为"发射信号的延迟版本"叠加上"多普勒调制"，再乘以散射系数（与 RCS 相关）。当场景中有多个目标时，接收信号是各目标回波的线性叠加。

在这种建模方式下，多普勒对 OFDM 正交性的破坏（即 ICI）会自然出现：因为多普勒会让一个 OFDM 符号内部产生相位旋转，导致子载波间能量泄漏。

这也是为什么在低信噪比或较大速度时，原始 RV 图里往往会出现旁瓣抬升、杂散等现象。

4. 4 发 4 收在这里"等效做了什么"？

在这里的 4Rx 处理采用了一个简单但常用的等效假设：

目标在阵列正前方，4 个接收通道对目标回波相位一致
每路接收叠加独立噪声
接收端把 4 路信号做相干合并（复数相加）

这等价于在不做角度估计/波束形成的情况下，直接获得一个 NRxN_{Rx}NRx 倍的阵列增益（噪声独立时 SNR 提升接近 10log⁡10NRxdB10\log_{10}N_{Rx} dB10log10NRxdB。

因此，在同样的"单路定义的 SNR"下，4Rx 合并后的 RV 图会更干净、目标峰更突出。

如果要更真实地体现阵列效应，需要引入阵元间距与目标方位角，4Rx 的相位会不同，合并前应进行角度相关补偿或波束形成；但当只关注距离-速度检测时，上述"同相合并"是一个合理的简化版本。

5. 接收处理链路：从 ISAC OFDM 到距离-速度图

5.1 "除去通信符号"的通道估计

由于 ISAC 场景下 OFDM 子载波上承载了通信数据符号 A(n,m)A(n,m)A(n,m)，直接对接收信号做 2D FFT 会把通信调制当成随机相位/幅度干扰。

因此常见处理是：

对每个 OFDM 符号做 FFT，得到 Y(n,m)Y(n,m)Y(n,m)
用已知的调制符号 A(n,m)A(n,m)A(n,m) 去"解调/消除"：

H(n,m)≈Y(n,m)A(n,m) H(n,m) \approx \frac{Y(n,m)}{A(n,m)} H(n,m)≈A(n,m)Y(n,m)

这样得到的 H(n,m)H(n,m)H(n,m) 更接近"雷达等效信道"，其中包含目标的时延与多普勒信息。

5.2 2D 变换形成 RV Map

接下来对 H(n,m)H(n,m)H(n,m) 做二维变换：

子载波维 IFFT → 距离域聚焦
慢时间维 FFT → 多普勒域聚焦

得到二维矩阵 Z(r,v)Z(r,v)Z(r,v)，即距离-速度图。

为了旁瓣控制，通常会在距离维和速度维分别加窗（如 Hamming 窗），以抑制泄漏与旁瓣。

原始 RV 图 展示的就是 Z(r,v)Z(r,v)Z(r,v) 的幅度（通常归一化后取 dB）。

6. 为什么需要"非相参积累"？它在 DDMA 里起什么作用？

DDMA 的关键副作用是：

由于不同 Tx 通道在多普勒维上被"分槽"或产生周期扩展，同一个物理目标的能量不会只集中在一个多普勒位置，而会分布到多个与 Tx 相关的子结构中。

因此，如果只看原始 RV 图，你会看到目标在速度维可能出现多个复制峰、或者能量被分散，导致单点峰值不够强、检测不够稳健。

6.1 子带划分（folding）

在 DDMA 中可以把速度维按发射通道数 NTxN_{Tx}NTx 划分成 NTxN_{Tx}NTx 个子带（每个子带长度 I=Ns/NTxI= N_s/N_{Tx}I=Ns/NTx）。

每个子带里包含同一物理目标的一个"对应分量"。把这些子带合并，就能恢复更集中的目标能量。

6.2 非相参积累

所谓"非相参"在这里采用的是一个计算简单、鲁棒的做法：对子带做复数直接相加（也可理解为一种不依赖精确相位对齐的合并策略）：

不需要估计每个子带间的精确相位关系
运算复杂度低
在低 SNR 下能显著提高目标可见性（等效提高检测统计量）

合并后的输出矩阵维度从 NsN_sNs 压缩为 III，速度轴也随之变为"折叠速度轴"。

DDMA MIMO OFDM ISAC：从回波模型到距离-速度图与非相参积累的原理梳理