数列的极限
- 一、数列的概念
- 二、数列极限的定义
-
- [1. 直观描述](#1. 直观描述)
- [2. 严格定义](#2. 严格定义)
- 三、数列极限定义的理解
- 四、举例说明
- 五、数列极限的性质
-
- [1. 唯一性](#1. 唯一性)
- [2. 有界性](#2. 有界性)
- [3. 保号性](#3. 保号性)
- [4. 夹逼定理(三明治定理)](#4. 夹逼定理(三明治定理))
- 六、实际应用情景
-
- [1. 计算机科学](#1. 计算机科学)
- [2. 金融学](#2. 金融学)
- [3. 物理学](#3. 物理学)
- [4. 工程技术](#4. 工程技术)
- 七、常用极限公式
- 八、典型例题
- 九、注意事项
一、数列的概念
定义
数列是按照一定顺序排列的一列数:
a 1 , a 2 , a 3 , ... , a n , ... a_1, a_2, a_3, \ldots, a_n, \ldots a1,a2,a3,...,an,...
记作 { a n } \{a_n\} {an},其中 a n a_n an 称为数列的通项 或一般项 , n n n 称为下标。
简单来说
数列就是一串有顺序的数字,比如:1, 1/2, 1/3, 1/4, ... 每个数字都有它的位置编号(第1个、第2个...)。
二、数列极限的定义
1. 直观描述
当 n n n 无限增大时,如果数列 { a n } \{a_n\} {an} 无限接近于某个确定的常数 A A A,则称 A A A 是数列 { a n } \{a_n\} {an} 的极限。
2. 严格定义
设 { a n } \{a_n\} {an} 是一个数列, A A A是一个常数。如果对于任意给定的正数 ε \varepsilon ε(无论它多么小),总存在正整数 N N N,使得当 n > N n > N n>N 时,都有:
∣ a n − A ∣ < ε |a_n - A| < \varepsilon ∣an−A∣<ε
成立,则称常数 A A A 是数列 { a n } \{a_n\} {an} 的极限,或称数列 { a n } \{a_n\} {an} 收敛于 A A A,记作:
lim n → ∞ a n = A 或 a n → A ( n → ∞ ) \lim_{n \to \infty} a_n = A \quad \text{或} \quad a_n \to A \ (n \to \infty) n→∞liman=A或an→A (n→∞)
如果这样的 A A A 不存在,则称数列发散。
三、数列极限定义的理解
将定义中的 ∣ a n − A ∣ < ε |a_n - A| < \varepsilon ∣an−A∣<ε去掉绝对值可得: A − ε < a n < A + ε A - \varepsilon <a_n< A + \varepsilon A−ε<an<A+ε
将数列 { a n } \{a_n\} {an}使用下面图形化的形式表示:
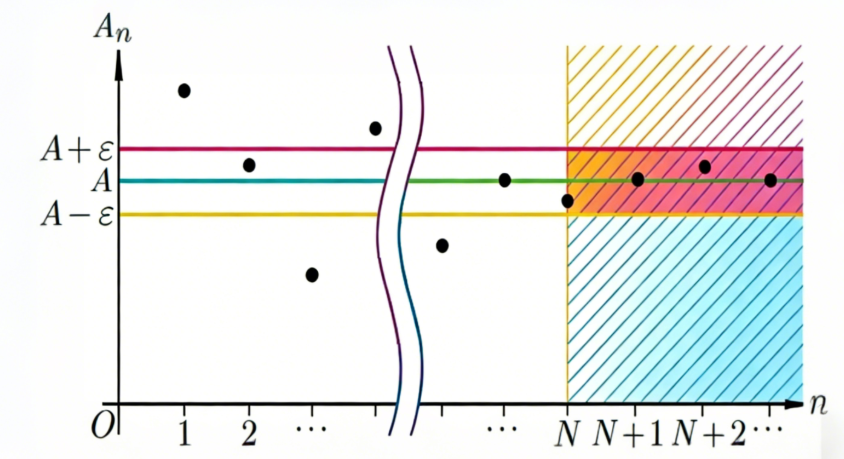
根据图形,数列极限的定义简单来说就是以 N N N为界线, N N N后面的所有项的值要在[ A − ε A - \varepsilon A−ε, A + ε A + \varepsilon A+ε]区间内,并且越来越靠近 A A A。为什么 ε \varepsilon ε要任意小呢?因为 ε \varepsilon ε越小越接近0, A + ε A + \varepsilon A+ε和 A − ε A - \varepsilon A−ε就越接近 A A A。
正整数 N N N就是区分"靠近 A A A"和"暂时没靠近 A A A"的关键界限,我们可以这样理解:
1.分界线之前( n < N n<N n<N):
- 这部分的数列项 a n a_n an,有可能不靠近 A A A。它们的取值可以是任意的,甚至和 A A A的差距比较大,极限定义不要求前面有限项的表现,只关注 n n n足够大之后的"长期
趋势"。
2.分界线之后( n > N n>N n>N):
- 从第 N + 1 N+1 N+1项开始,所有的 a n a_n an必须落在 A A A的 ε \varepsilon ε邻域内(也就是 a n − A < e a_n-A<e an−A<e),这才是"靠近 A A A"的核心要求。
例如:
数列 a n = { 100 , n ≤ 1000 1 n , n > 1000 a_n = \begin{cases} 100, & n \le 1000 \\ \frac{1}{n}, & n > 1000 \end{cases} an={100,n1,n≤1000n>1000它的极限是 0 0 0。
这里的"分界线" N N N可以取 1000 1000 1000,前1000项都等于100,离0很远;但从第1001项开始, a n a_n an会越来越靠近0,满足极限的要求。
所以总结来说:分界线之前的有限项可以不靠近 A A A。但分界线之后的所有项必须无限靠近 A A A,
极限是一种趋势,不是具体的值。例如:
lim 馅 → 0 包子 = 馒头 \lim_{\text{馅} \to 0} \text{包子} = \text{馒头} 馅→0lim包子=馒头
这个表达的是一种趋势,并不是具体的值。
四、举例说明
例1:证明 lim n → ∞ 1 n = 0 \lim_{n \to \infty} \frac{1}{n} = 0 limn→∞n1=0
解题过程:
-
分析 :对于任意给定的 ε > 0 \varepsilon > 0 ε>0,要使:
∣ 1 n − 0 ∣ = 1 n < ε \left| \frac{1}{n} - 0 \right| = \frac{1}{n} < \varepsilon n1−0 =n1<ε只需 n > 1 ε n > \frac{1}{\varepsilon} n>ε1
-
证明:
- 任取 ε > 0 \varepsilon > 0 ε>0
- 取 N = [ 1 ε ] + 1 N = \left[ \frac{1}{\varepsilon} \right] + 1 N=[ε1]+1(方括号表示取整)
- 当 n > N n > N n>N 时,有 n > 1 ε n > \frac{1}{\varepsilon} n>ε1,所以:
∣ 1 n − 0 ∣ = 1 n < ε \left| \frac{1}{n} - 0 \right| = \frac{1}{n} < \varepsilon n1−0 =n1<ε - 根据定义, lim n → ∞ 1 n = 0 \lim_{n \to \infty} \frac{1}{n} = 0 limn→∞n1=0
例2:证明 lim n → ∞ n n + 1 = 1 \lim_{n \to \infty} \frac{n}{n+1} = 1 limn→∞n+1n=1
解题过程:
-
分析 :对于任意给定的 ε > 0 \varepsilon > 0 ε>0,要使:
∣ n n + 1 − 1 ∣ = ∣ − 1 n + 1 ∣ = 1 n + 1 < ε \left| \frac{n}{n+1} - 1 \right| = \left| -\frac{1}{n+1} \right| = \frac{1}{n+1} < \varepsilon n+1n−1 = −n+11 =n+11<ε只需 n + 1 > 1 ε n+1 > \frac{1}{\varepsilon} n+1>ε1,即 n > 1 ε − 1 n > \frac{1}{\varepsilon} - 1 n>ε1−1
-
证明:
- 任取 ε > 0 \varepsilon > 0 ε>0
- 取 N = [ 1 ε − 1 ] + 1 N = \left[ \frac{1}{\varepsilon} - 1 \right] + 1 N=[ε1−1]+1
- 当 n > N n > N n>N 时,有 n > 1 ε − 1 n > \frac{1}{\varepsilon} - 1 n>ε1−1,即 n + 1 > 1 ε n+1 > \frac{1}{\varepsilon} n+1>ε1
- 所以:
∣ n n + 1 − 1 ∣ = 1 n + 1 < ε \left| \frac{n}{n+1} - 1 \right| = \frac{1}{n+1} < \varepsilon n+1n−1 =n+11<ε - 根据定义,极限为1
例3:判断数列 a n = ( − 1 ) n a_n = (-1)^n an=(−1)n 的敛散性
分析 :
a n = { 1 , n 为偶数 − 1 , n 为奇数 a_n = \begin{cases} 1, & n \text{为偶数} \\ -1, & n \text{为奇数} \end{cases} an={1,−1,n为偶数n为奇数
这个数列在1和-1之间振荡,不会无限接近任何一个常数,所以发散。
五、数列极限的性质
1. 唯一性
如果数列收敛,那么它的极限是唯一的。
2. 有界性
如果数列收敛,那么它一定有界(即存在常数 M M M,使得 ∣ a n ∣ ≤ M |a_n| \leq M ∣an∣≤M 对所有 n n n 成立)。
注意:有界数列不一定收敛(如例3中的振荡数列)。
3. 保号性
如果 lim n → ∞ a n = A > 0 \lim_{n \to \infty} a_n = A > 0 limn→∞an=A>0,那么存在 N N N,当 n > N n > N n>N 时,有 a n > 0 a_n > 0 an>0。
类似地,如果 A < 0 A < 0 A<0,则从某项开始 a n < 0 a_n < 0 an<0。
4. 夹逼定理(三明治定理)
如果数列 { b n } \{b_n\} {bn}、 { a n } \{a_n\} {an}、 { c n } \{c_n\} {cn} 满足:
b n ≤ a n ≤ c n ( 从某项开始 ) b_n \leq a_n \leq c_n \quad (\text{从某项开始}) bn≤an≤cn(从某项开始)
且 lim n → ∞ b n = lim n → ∞ c n = A \lim_{n \to \infty} b_n = \lim_{n \to \infty} c_n = A limn→∞bn=limn→∞cn=A,
那么 lim n → ∞ a n = A \lim_{n \to \infty} a_n = A limn→∞an=A。
六、实际应用情景
1. 计算机科学
- 算法复杂度:大O符号中,极限描述算法性能随输入规模增长的趋势
- 数值计算:迭代法求方程的近似解,数列的极限就是精确解
2. 金融学
- 复利计算 :连续复利公式 A = P e r t A = P e^{rt} A=Pert 可通过数列极限推导
设每年计息 n n n 次,本息和为:
A n = P ( 1 + r n ) n A_n = P \left(1 + \frac{r}{n}\right)^n An=P(1+nr)n
当 n → ∞ n \to \infty n→∞ 时:
lim n → ∞ A n = P e r \lim_{n \to \infty} A_n = P e^{r} n→∞limAn=Per
3. 物理学
- 瞬时速度:平均速度数列的极限就是瞬时速度
设物体在 t t t 到 t + Δ t t+\Delta t t+Δt 时间内位移为 Δ s \Delta s Δs,则平均速度:
v 平均 = Δ s Δ t v_{\text{平均}} = \frac{\Delta s}{\Delta t} v平均=ΔtΔs
当 Δ t → 0 \Delta t \to 0 Δt→0 时(对应 n → ∞ n \to \infty n→∞ 的数列),极限就是瞬时速度。
4. 工程技术
- 信号处理:滤波器的响应随频率变化的极限特性
- 控制系统:系统响应的稳态值就是时间趋于无穷时的极限
七、常用极限公式
- lim n → ∞ 1 n p = 0 ( p > 0 ) \lim_{n \to \infty} \frac{1}{n^p} = 0 \quad (p > 0) limn→∞np1=0(p>0)
- lim n → ∞ q n = 0 ( ∣ q ∣ < 1 ) \lim_{n \to \infty} q^n = 0 \quad (|q| < 1) limn→∞qn=0(∣q∣<1)
- lim n → ∞ a n = 1 ( a > 0 ) \lim_{n \to \infty} \sqrt[n]{a} = 1 \quad (a > 0) limn→∞na =1(a>0)
- lim n → ∞ n n = 1 \lim_{n \to \infty} \sqrt[n]{n} = 1 limn→∞nn =1
- lim n → ∞ ( 1 + 1 n ) n = e \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e limn→∞(1+n1)n=e(重要极限)
八、典型例题
例4 :用夹逼定理求 lim n → ∞ 1 n 2 + 1 + 1 n 2 + 2 + ⋯ + 1 n 2 + n \lim_{n \to \infty} \frac{1}{\sqrt{n^2+1}} + \frac{1}{\sqrt{n^2+2}} + \cdots + \frac{1}{\sqrt{n^2+n}} limn→∞n2+1 1+n2+2 1+⋯+n2+n 1
解:
- 设 a n = ∑ k = 1 n 1 n 2 + k a_n = \sum_{k=1}^n \frac{1}{\sqrt{n^2+k}} an=∑k=1nn2+k 1
- 注意到:
n n 2 + n ≤ a n ≤ n n 2 + 1 \frac{n}{\sqrt{n^2+n}} \leq a_n \leq \frac{n}{\sqrt{n^2+1}} n2+n n≤an≤n2+1 n - 计算两边的极限:
lim n → ∞ n n 2 + n = lim n → ∞ 1 1 + 1 n = 1 \lim_{n \to \infty} \frac{n}{\sqrt{n^2+n}} = \lim_{n \to \infty} \frac{1}{\sqrt{1+\frac{1}{n}}} = 1 n→∞limn2+n n=n→∞lim1+n1 1=1
lim n → ∞ n n 2 + 1 = lim n → ∞ 1 1 + 1 n 2 = 1 \lim_{n \to \infty} \frac{n}{\sqrt{n^2+1}} = \lim_{n \to \infty} \frac{1}{\sqrt{1+\frac{1}{n^2}}} = 1 n→∞limn2+1 n=n→∞lim1+n21 1=1 - 由夹逼定理得: lim n → ∞ a n = 1 \lim_{n \to \infty} a_n = 1 limn→∞an=1
例5 :判断数列 a n = sin n n a_n = \frac{\sin n}{n} an=nsinn 的敛散性
解:
- 因为 ∣ sin n ∣ ≤ 1 |\sin n| \leq 1 ∣sinn∣≤1,所以:
∣ a n ∣ = ∣ sin n n ∣ ≤ 1 n |a_n| = \left|\frac{\sin n}{n}\right| \leq \frac{1}{n} ∣an∣= nsinn ≤n1 - 而 lim n → ∞ 1 n = 0 \lim_{n \to \infty} \frac{1}{n} = 0 limn→∞n1=0
- 由夹逼定理: lim n → ∞ ∣ a n ∣ = 0 \lim_{n \to \infty} |a_n| = 0 limn→∞∣an∣=0,所以 lim n → ∞ a n = 0 \lim_{n \to \infty} a_n = 0 limn→∞an=0
- 数列收敛于0
九、注意事项
- 极限存在 vs 有界:
- 收敛 ⇒ 有界
- 有界 ⇏ 收敛(如 ( − 1 ) n (-1)^n (−1)n)
- 无穷大不是极限:
说"极限是无穷大"只是习惯说法,严格来说,极限不存在(发散到无穷)。
- 证明极限的步骤:
- 给定 ε > 0 \varepsilon > 0 ε>0
- 解不等式 ∣ a n − A ∣ < ε |a_n - A| < \varepsilon ∣an−A∣<ε,找到 N N N 与 ε \varepsilon ε 的关系
- 取合适的 N N N(通常取整+1)
- 验证 n > N n > N n>N 时不等式成立