线性回归模型常用的评价指标如表1所示。如果建立模型时使用的是同样的已知数据集,模型之间就可以互相比较。
要想打好机器学习的数学基础,请参见清华大学出版社的人人可懂系列,包括《人人可懂的微积分》(已上市)、《人人可懂的线性代数》(即将上市)、《人人可懂的概率统计》(即将上市)。

表1 线性回归模型常用的评价指标
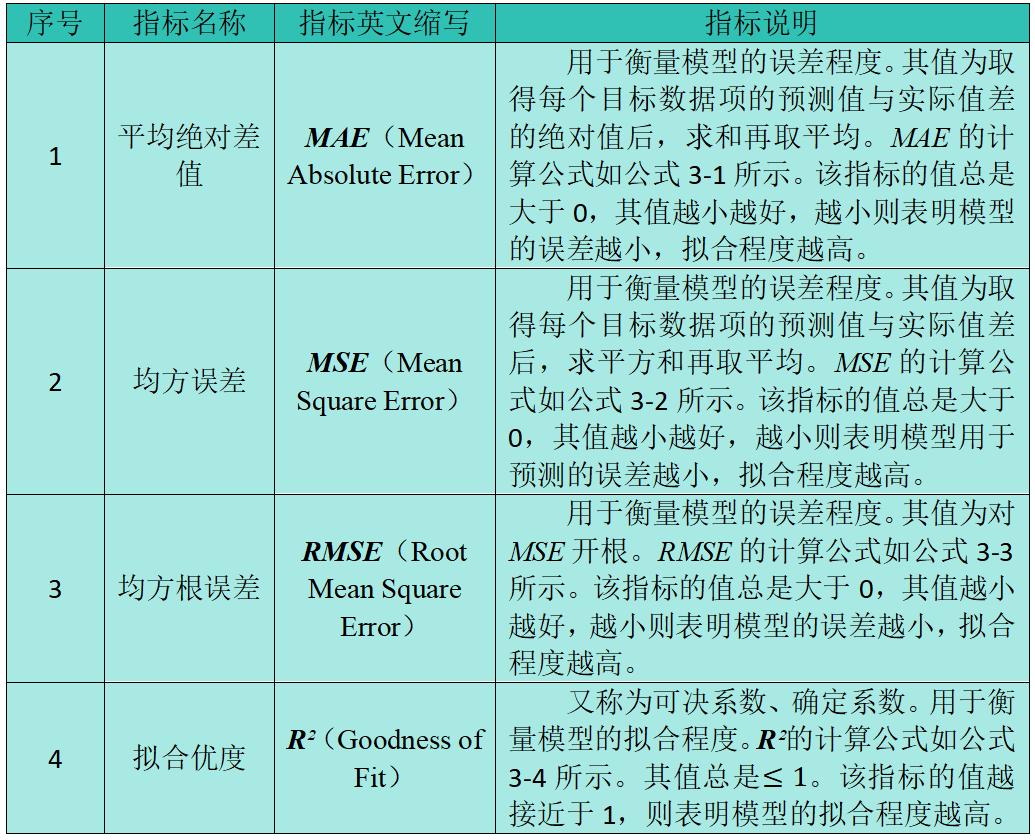
表1的英文中,"Mean"的中文意思为"平均值";"Absolute"的中文意思为"绝对的";"Error"的中文意思为"误差";"Root"的中文意思为"根";"Goodness"的中文意思为"优秀的程度";"Fit"的中文意思为"拟合"。
**提示:**思来想去,在这里还是列出了这些评价指标的计算公式,如果一下还看不明白,就先学会用,在用的过程中再体会其含义。
MAE = 1 m ∑ i = 0 m − 1 ∣ y p i − y ti ∣ = 1 m ∑ i = 0 m − 1 ∣ y p i − y i ∣ \mathbf{\text{MAE}} = \frac{1}{m}\sum_{i = 0}^{m - 1}\left| y_{pi} - y_{\text{ti}} \right| = \frac{1}{m}\sum_{i = 0}^{m - 1}\left| y_{pi} - y_{i} \right| MAE=m1i=0∑m−1∣ypi−yti∣=m1i=0∑m−1∣ypi−yi∣
(公式1)
公式1中,数据项的下标从0开始至m -1; y pi y_{\text{pi}} ypi表示第 i i i个目标数据项的预测值,p 为英文单词"predict"的首字母,"predict"的中文意思是"预测"; y ti y_{\text{ti}} yti表示第 i i i个目标数据项的真实值,t 为英文单词"true"的首字母。在不影响理解的前提下, y ti y_{\text{ti}} yti可简化的表达为 y i y_{i} yi。
看到∑这种符号不用紧张,理解就好,理解了后会发现其实很简单。那么怎么理解∑(念"希格码")这个运算符号呢?这个运算符号表示求和,也即累加。符号中的下标表示求和表达式中变量的起始值,上标表示求和表达式中变量的结束值,这个变量也可以是求和表达式中的元素下标、上标。如:
∑ i = 1 n i = 1 + 2 + ... + n \sum_{i = 1}^{n}i = 1 + 2 + \ldots + n i=1∑ni=1+2+...+n
∑ i = 1 n x i = x 1 + x 2 + ... + x n \sum_{i = 1}^{n}x^{i} = x^{1} + x^{2} + \ldots + x^{n} i=1∑nxi=x1+x2+...+xn
接下来看MSE 的计算公式。公式2中,为什么用平方呢?因为用平方后,可以确保 ( y pi − y i ) 2 \left( y_{\text{pi}} - y_{i} \right)^{2} (ypi−yi)2的值会大于或等于0,肯定不会是负数。而在非负数中,数的平方及其绝对值变化方向一致,且平方的表示法会在导数(涉及到了高等数学的内容,如果不理解就跳过)计算时带来便利。所以在很多应用场景中,会使用平方这种计算方式。
M S E = 1 m ∑ i = 0 m − 1 ( y pi − y i ) 2 \mathbf{M}\mathbf{S}\mathbf{E} = \frac{1}{m}\sum_{i = 0}^{m - 1}\left( y_{\text{pi}} - y_{i} \right)^{2} MSE=m1i=0∑m−1(ypi−yi)2
(公式2)
RM S E = 1 m ∑ i = 0 m − 1 ( y pi − y i ) 2 \mathbf{\text{RM}}\mathbf{S}\mathbf{E} = \sqrt{\frac{1}{m}\sum_{i = 0}^{m - 1}\left( y_{\text{pi}} - y_{i} \right)^{2}} RMSE=m1i=0∑m−1(ypi−yi)2
(公式3)
R 2 = 1 − ∑ i = 0 m − 1 ( y pi − y i ) 2 ∑ i = 0 m − 1 ( y i − y t ‾ ) 2 \mathbf{R}^{2} = 1 - \frac{\sum_{i = 0}^{m - 1}\left( y_{\text{pi}} - y_{i} \right)^{2}}{\sum_{i = 0}^{m - 1}\left( y_{i} - \overline{y_{t}} \right)^{2}} R2=1−∑i=0m−1(yi−yt)2∑i=0m−1(ypi−yi)2
= 1 − ( 1 m ∑ i = 0 m − 1 ( y pi − y i ) 2 ) ( 1 m ∑ i = 0 m − 1 ( y i − y t ‾ ) 2 ) = 1 - \frac{\left( \frac{1}{m}\sum_{i = 0}^{m - 1}\left( y_{\text{pi}} - y_{i} \right)^{2} \right)}{\left( \frac{1}{m}\sum_{i = 0}^{m - 1}\left( y_{i} - \overline{y_{t}} \right)^{2} \right)} =1−(m1∑i=0m−1(yi−yt)2)(m1∑i=0m−1(ypi−yi)2)
= 1 − MSE Var = 1 - \frac{\mathbf{\text{MSE}}}{\mathbf{\text{Var}}} =1−VarMSE
(公式4)
要想打好机器学习的数学基础,请参见清华大学出版社的人人可懂系列,包括《人人可懂的微积分》(已上市)、《人人可懂的线性代数》(即将上市)、《人人可懂的概率统计》(即将上市)。
y t ‾ \overline{y_{t}} yt表示所有目标数据项真实值的平均值。从公式4来看,拟合优度又与MSE 与Var (方差)的比值存在关联关系。方差用于衡量目标数据项值的离散程度,越大表明值越离散。通常,通过拟合后,模型目标数据项的预测值与真实值误差的程度会比目标数据项值的离散程度要小,所以 R 2 \mathbf{R}^{2} R2通常会 ≤ 1 \leq 1 ≤1。其中,分式的值越在正数范围内接近于0,则 R 2 R^{2} R2的值就越接近于1,表明拟合程度越高。但是有时,分式的值也会大于1,此时会使得 R 2 \mathbf{R}^{2} R2的值小于0,表明模型目标数据项的预测值与真实值误差的程度比目标数据项值的离散程度还要大,模型的拟合程度是很差的。