目录
无穷级数是复变函数的基础之一,本质是无穷多项的数列相加求和的模型,其研究的重点在于如何判断一个级数的敛散性,即一个级数在写到无穷多项后,他们的和是否会越来越逼近一个具体的数,称为收敛;或者是不断振荡变化没有一个确定的值,称为发散。
无穷级数通常分常数项级数、函数项级数。其中常数项级数又可以分为正项级数、交错级数、任意项级数等等;而函数项级数通常有幂级数、傅里叶级数。其中傅里叶级数在前面的文章中有详细介绍,所以本篇文章将聚焦于前4种级数,学习常数项级数的性质、正项级数的4种审敛法,以及函数项级数的收敛半径等等。
一、常数项级数的4大基本性质
只要是常数项级数,不管他是正项级数还是交错级数亦或是任意项级数都满足以下基本性质:
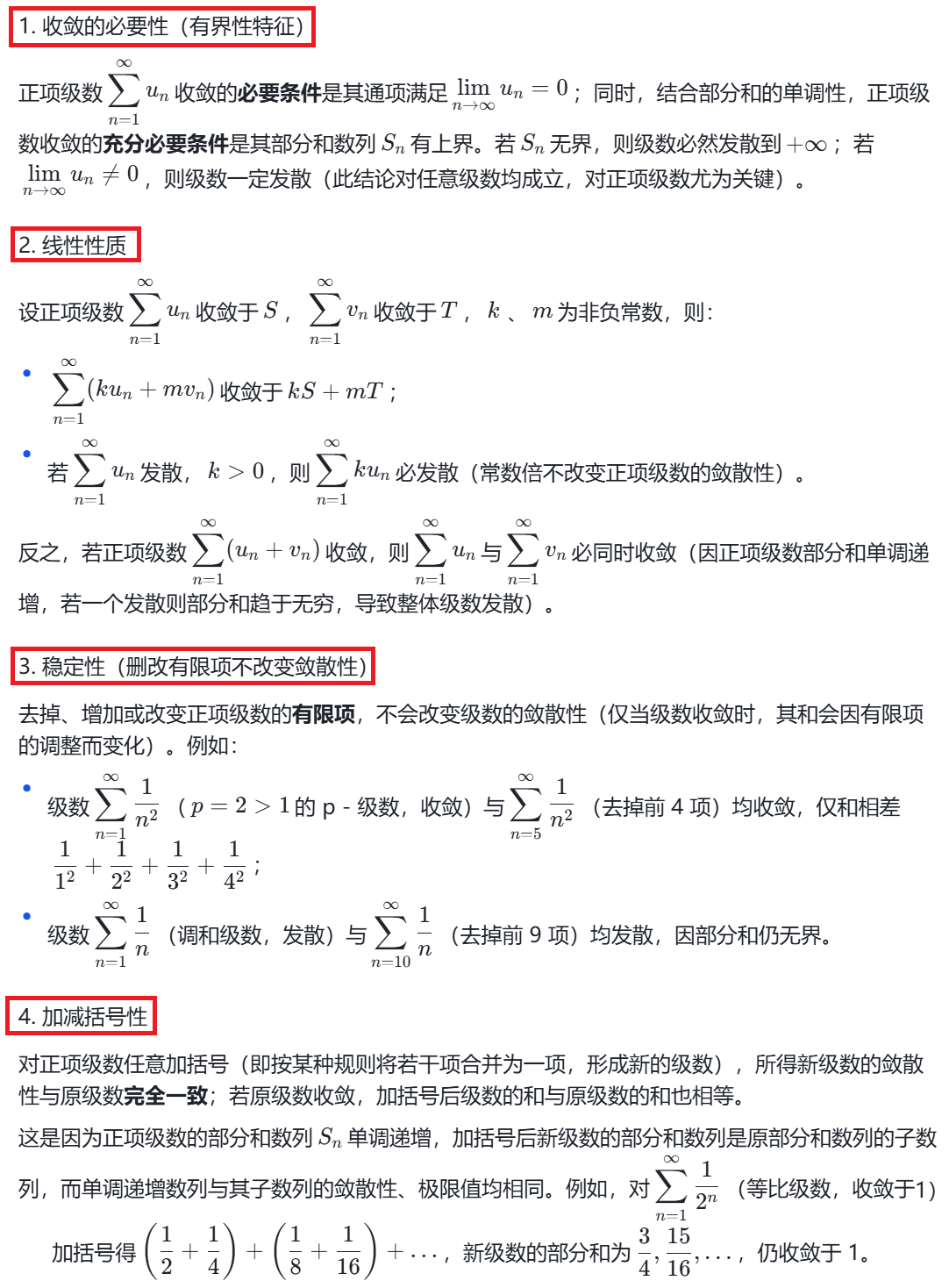
注意:这里面最重要的性质就是必要性,他是后续判断级数敛散性的第一步,如果区域无穷时,项值连趋近于0这个必要性都不满足,那么该级数必定发散。至于其他的性质有所印象即可,要用的时候自己推导思考一下很快能得出结论。
二、正项级数的4种审敛方法
正项级数作为常数项级数的重要组成部分,其审敛法在后续具有指导意义。通常有比较审敛法、比较审敛法的极限形式、比值审敛法、根值审敛法。
其中,后3种审敛法都是因为级数的收敛性只与尾部收敛性相关。即虽然这里我们说是n趋近于∞,但这仅仅表明n是一个很大很大的常数,在系统稳定后,从第n+1项开始往后求和,只要尾部是收敛的则整体级数收敛。至于前面的n尽管再大也只是一个确定的常数,仅仅影响级数的收敛值,而不影响收敛性。所以我们说正数项级数的敛散性只由尾部决定。这也是理解各种审敛法的基本原理。
(1)比较审敛法
顾名思义,就是找到一个已知审敛性的级数V(n)和自己U(n)对比,通常找的函数会与自己的形式高度相似,从从而有V(n)、U(n)的大小关系保持恒定不变。
然后利用线性性质:大敛则小敛、小发则大发来判断敛散性。

(2)比较审敛法的极限形式
刚刚的比较审敛法是严格保证了通项的大小关系,但是这样太过苛刻,很多时候你不好找到一个完美的通项,但是比较审敛法的极限形式告诉我们:只要你能找到一个已知审敛性的函数,然后在极限处判断出大小关系,**即收敛性仍然是由尾部决定的。**而这里说的极限形式,其实就是找到了一个很大很大的常数,在这之后都满足大小比较关系,并非真的n无限趋近于∞。
正是因此,所以比较审敛法的极限形式往往比一般比较审敛法更加通用,只要你能判断尾部的收敛性,就能知道级数的收敛性。

(3)比值审敛法
比较审敛法仍然是需要你有足够的知识储备,知道常见函数的收敛性,然后用它作为对比得到的,而比值审敛法则更加自给自足,他不需要你找任何对比函数,而是自身的后一项和前一项相比。即在n大于某个很大的值时,有后项>前项恒成立,则呈现收敛趋势。
就好比在银行存钱,不管你前面n期的利率有多么高或者多么惨,但是从n+1期开始,单期利率始终小于1,那么你的钱经过长时间后就会清零,而我们说求和符号是把每一期的总金额加到一起,所以这里的和值并非是最后一期的总金额,而是每一期的总金额求和,大概率是一个不等于0的常数;而从n+1期开始,单期利率始终大于1,则经过足够长时间后,你的钱会呈现越来越多的发散状态。

(4)根值审敛法
比值审敛法看的是长期后的单期利率,而根值审敛法看的则是长期的平均利率。即第n期以后,只要他开n次根号,得到长期下来的平均利率是大于1的则发散;而得到的平均利率是小于1的则收敛。

三、交错级数审敛法---莱布尼兹判别法
交错级数是指符号为一正一负的级数,前面的正项级数审敛法在此并不适用。莱布尼兹审敛法就好比一个测距机器人正在测量桌子的长度:每次走的步长都是正数,但是在桌子边缘处发现不能刚好与边缘对齐,所以形成来回走的样子,但每次的步长都会比上次短,所以能精准测量出桌子的长度。
而如果步长没有逐渐变小至0的趋势,即级数不单调递减,比如是一个常数,那么该机器人始终会在一种状态兜圈子,误差就是此时的常数步长。
四、幂级数及收敛半径

(1)阿贝尔定理

简单来说,就是你如果找到了一个x0为收敛点,则其内部都是绝对收敛的(绝对收敛是收敛的更严苛形式,加绝对值收敛、本身也收敛,同时由绝对收敛可以推导出本身收敛);如果你找到了一个发散点x0,那么从x0开始往外的全都发散。
而这里说在R的端点处敛散性不确定,其实是题目仅仅告诉你收敛半径,而没有告诉你收敛点的情况。
(2)收敛半径的求法
很多教科书会给出公式法和比值法。但其实公式法就是比值法的特殊情况。对于一个任意级数(可能是缺项级数),你只需要给他们的每一项都加绝对值让其成为正项级数,于是就能使用正项级数的比值审敛法,找到一个x0点使其收敛,而x0处绝对收敛了则说明本身收敛(绝对收敛的定义)。
然后通过阿贝尔定理可知:x0处收敛则其内部绝对收敛。所以就得到了一个完整的收敛半径。
下面这个是公式法,但是我觉得不好理解,推荐大家以后不论有没有缺项,就在加绝对值后使用比值审敛法、根值审敛法(因为比值法和根值法都会把x的次方约去几乎大部分)即可。
