二叉树经典OJ题

1.前序遍历https://leetcode.cn/problems/binary-tree-preorder-traversal

---

TreeSize 函数

int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->right) + TreeSize(root->left) + 1;
}

• 功能：递归计算二叉树的节点总数。
• 逻辑 ：
  • 若当前节点为 NULL，返回 0。
  • 否则，返回左子树节点数 + 右子树节点数 + 1（当前节点）。

---

preorder 函数

void preorder(struct TreeNode* root, int* a, int* pi)
{
    if(root == NULL)
      return;
    a[(*pi)++] = root->val;
    preorder(root->left, a, pi);
    preorder(root->right, a, pi);
}

• 功能 ：递归实现前序遍历，将节点值存入数组 a。
• 逻辑 ：
  • 若当前节点为 NULL，直接返回。
  • 将当前节点的值 root->val 存入数组 a，并递增索引 pi。
  • 递归遍历左子树和右子树。

---

preorderTraversal 函数

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(sizeof(int) * (*returnSize));
    int i = 0;
    preorder(root, a, &i);
    return a;
}

• 功能：主函数，分配内存并调用前序遍历。
• 逻辑 ：
  • 调用 TreeSize 获取二叉树节点数，存入 returnSize。
  • 动态分配数组 a，大小为 *returnSize。
  • 调用 preorder 填充数组，返回结果。

---

关键点说明

1. 动态内存分配 ：通过 malloc 分配数组空间，需确保后续释放内存（调用方负责）。
2. 索引传递 ：使用指针 int* pi 维护当前写入位置，避免全局变量。
3. 前序遍历顺序：根节点 → 左子树 → 右子树。

完整代码：

int TreeSize(struct TreeNode* root) 
{
    if (root == NULL) return 0;
    return TreeSize(root->left) + TreeSize(root->right) + 1;
}

void preorder(struct TreeNode* root, int* a, int* pi) 
{
    if (root == NULL) return;
    
    a[(*pi)++] = root->val;
    preorder(root->left, a, pi);
    preorder(root->right, a, pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{
    *returnSize = TreeSize(root);
    int* a = (int*)malloc(sizeof(int) * (*returnSize));
    int i = 0;
    
    preorder(root, a, &i);
    return a;
}
 

---

2.相同的树https://leetcode.cn/problems/same-tree

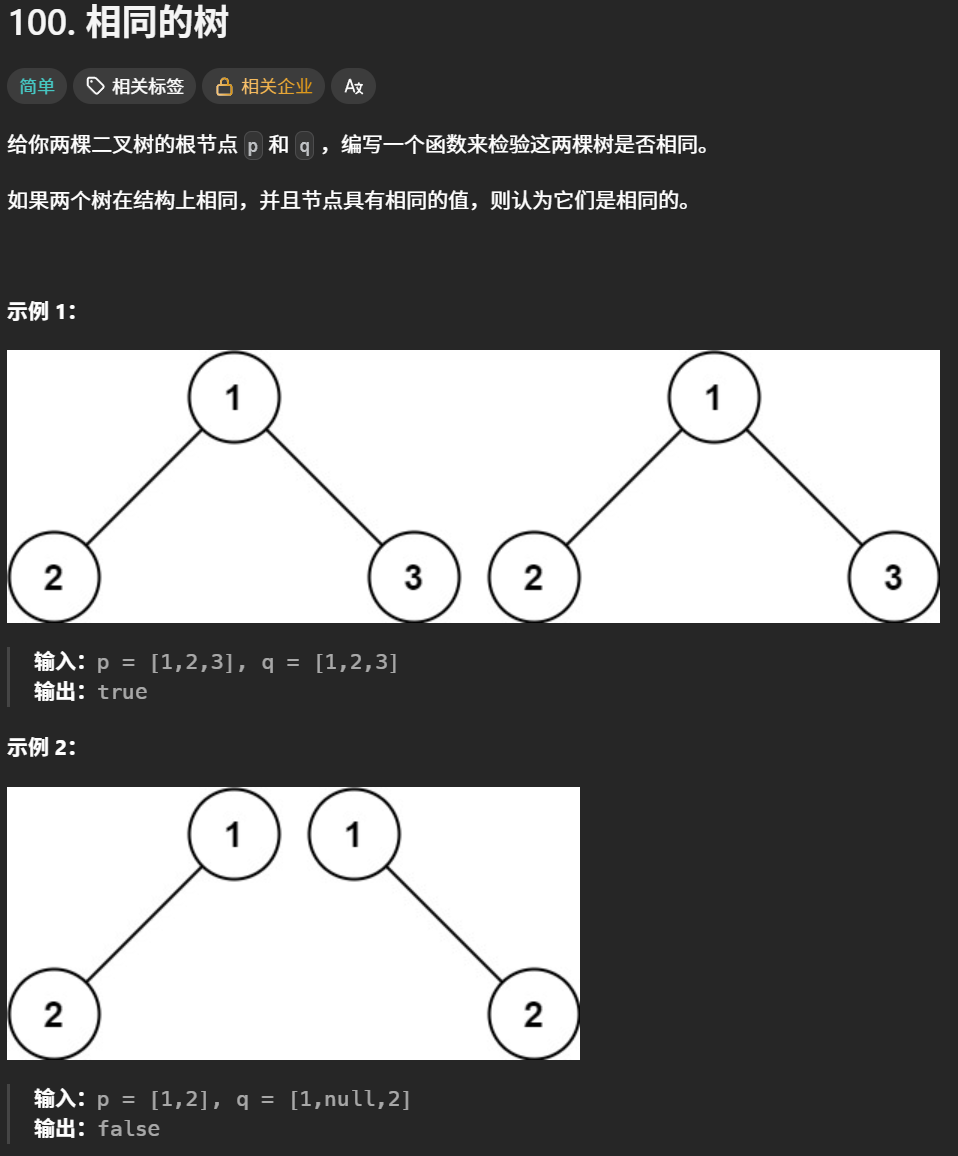
递归终止条件

当两个节点都为空指针时，说明当前分支已经遍历到底部且完全匹配，返回true。

if(p == NULL && q ==NULL)
    return true;

当只有一个节点为空时，说明树结构不一致，返回false。

if(p == NULL || q == NULL)
    return false;

节点值比较

当前两个节点都存在时，比较它们的值。如果值不相等，立即返回false。

if(p->val != q->val)
    return false;

递归子树比较

当当前节点值和结构都匹配时，递归比较左右子树。只有左右子树都完全匹配时才返回true。

return isSameTree(p->right,q->right) && isSameTree(p->left,q->left);

完整代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    // 如果两棵树都为空，则相同
    if (p == NULL && q == NULL) {
        return true;
    }
    
    // 如果其中一棵树为空而另一棵不为空，则不同
    if (p == NULL || q == NULL) {
        return false;
    }
    
    // 比较当前节点的值
    if (p->val != q->val) {
        return false;
    }
    
    // 递归比较左右子树
    return isSameTree(p->right, q->right) && isSameTree(p->left, q->left);
}
 

3.对称二叉树https://leetcode.cn/problems/symmetric-tree

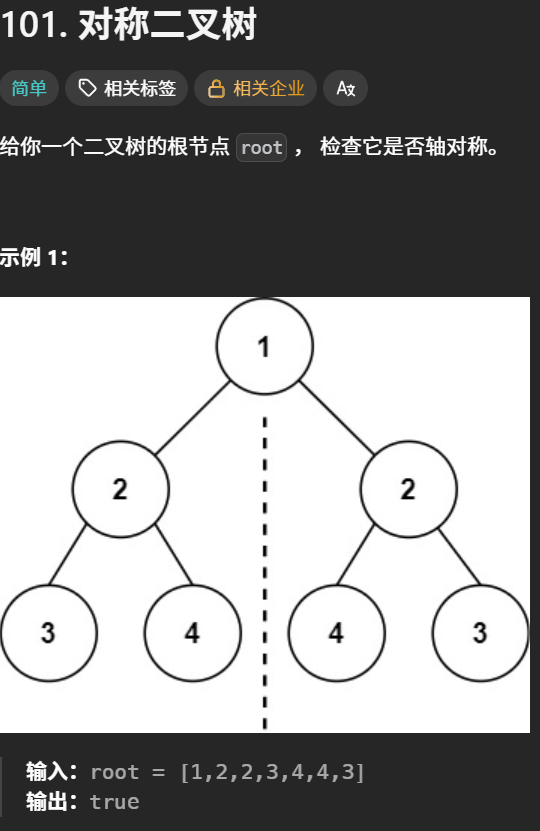
辅助函数 _isSymmetric

bool _isSymmetric(struct TreeNode* left, struct TreeNode* right)
{
    if(left == NULL && right == NULL)
        return true;
    if(left == NULL || right == NULL)
        return false;
    return left->val == right->val
        && _isSymmetric(left->left, right->right)
        && _isSymmetric(left->right, right->left);
}

该递归函数比较两个子树是否互为镜像：

• 两个节点都为空时返回true
• 只有一个节点为空时返回false
• 比较当前节点值，并递归比较左子树的左孩子与右子树的右孩子，以及左子树的右孩子与右子树的左孩子

主函数 isSymmetric

bool isSymmetric(struct TreeNode* root){
    if(root == NULL)
        return true;
    return _isSymmetric(root->left, root->right);
}

该函数处理边界情况（空树），然后调用辅助函数比较根节点的左右子树。

时间复杂度分析

该算法需要遍历所有节点一次，时间复杂度为O(n)，其中n是树中节点数量。

空间复杂度分析

最坏情况下（完全不平衡树）递归调用栈的深度为O(n)，最好情况下（完全平衡树）为O(log n)。

4.另一颗树的子树https://leetcode.cn/problems/subtree-of-another-tree

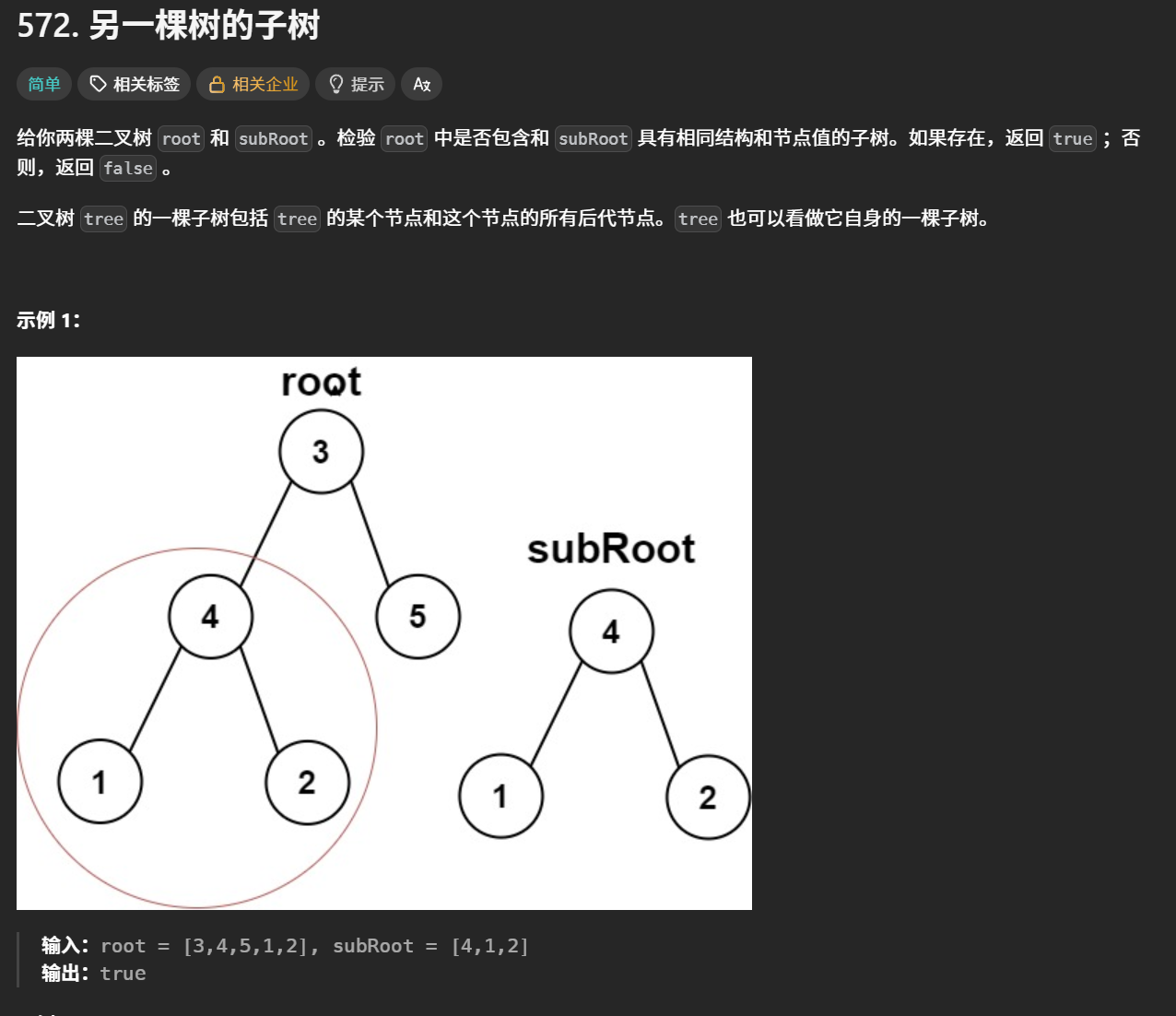
分析

1.判断两棵二叉树是否完全相同（isSameTree函数）

2判断一棵树是否是另一棵树的子树（isSubtree函数）

isSameTree函数采用递归方式比较两棵二叉树的结构和节点值：

• 两棵树均为空时返回true。
• 仅一棵树为空时返回false。
• 当前节点值不同时返回false。
• 递归比较左右子树是否相同。

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if (p == NULL && q == NULL) return true;
    if (p == NULL || q == NULL) return false;
    if (p->val != q->val) return false;
    return isSameTree(p->right, q->right) && isSameTree(p->left, q->left);
}

判断子树（isSubtree）

isSubtree函数通过遍历主树来查找与子树根节点值相同的节点，并验证子树结构：

• 主树为空时直接返回false。
• 发现节点值与子树根相同时，调用isSameTree验证整棵子树。
• 递归搜索主树的左右子树。

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if(root == NULL) return false;
    if(root->val == subRoot->val && isSameTree(root,subRoot))
        return true;
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

时间复杂度分析

• isSameTree: 最坏情况需遍历所有节点，时间复杂度为O(n)，n为节点数。
• isSubtree : 对于主树的每个节点都可能调用isSameTree，最坏时间复杂度为O(m×n)，m和n分别为主树和子树的节点数。

完整代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    // 两树均为空时相同
    if (!p && !q) return true;
    
    // 仅一棵树为空时不同
    if (!p || !q) return false;
    
    // 节点值不同则树不同
    if (p->val != q->val) return false;
    
    // 递归检查左右子树
    return isSameTree(p->right, q->right) && isSameTree(p->left, q->left);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if (!root) return false;
    
    // 当前节点匹配且子树相同
    if (root->val == subRoot->val && isSameTree(root, subRoot)) {
        return true;
    }
    
    // 递归检查左右子树
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}
 

5.二叉树遍历https://www.nowcoder.com/share/jump/8952502741769268534244

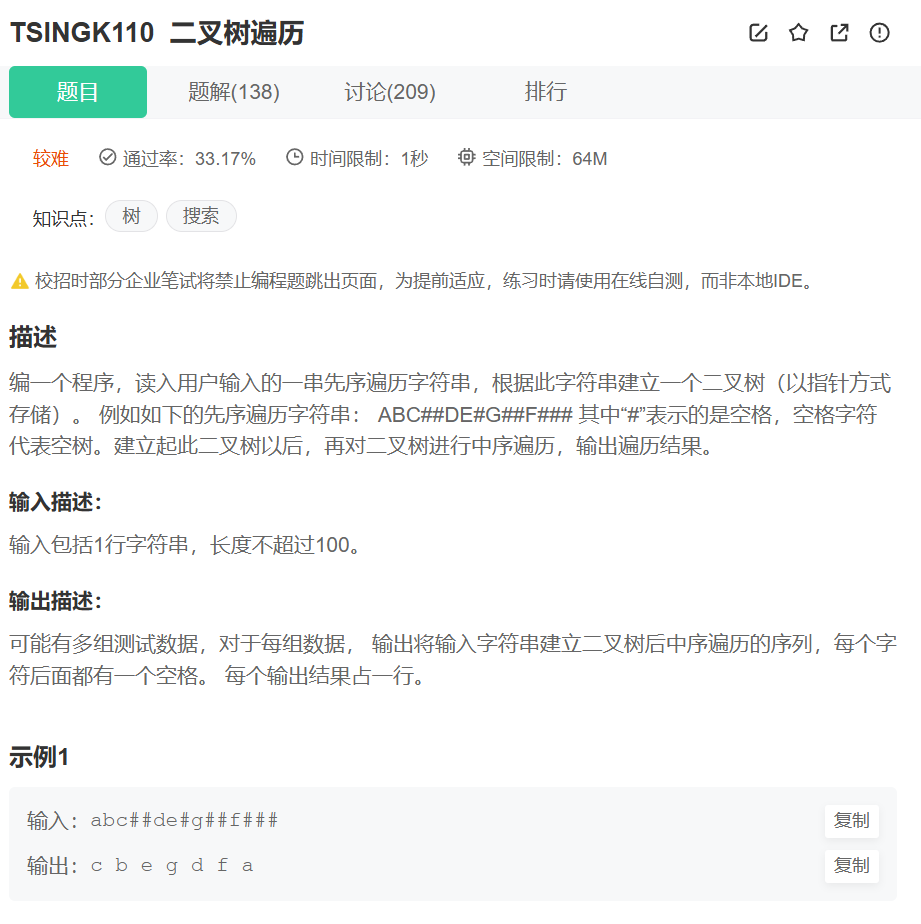
二叉树节点结构体

typedef struct TreeNode
{
    char val;
    struct TreeNode* left;
    struct TreeNode* right;
}TreeNode;

定义了一个二叉树节点结构体，包含：

• val：存储字符类型的节点值
• left：指向左子节点的指针
• right：指向右子节点的指针

二叉树构建函数

TreeNode* maketree(char* arr, int* count)
{
    if(arr[*count]=='#' || arr[*count]=='\0')
    {
        return NULL;
    }
    TreeNode* newnode = (TreeNode*)malloc(sizeof(TreeNode));
    newnode->val = arr[(*count)++];
    
    newnode->left = maketree(arr,count);
    (*count)++;
    newnode->right = maketree(arr,count);
    return newnode;
}

该函数通过递归方式构建二叉树：

• 输入参数为字符数组arr和整数指针count（用于跟踪当前处理的字符位置）
• 遇到#或空字符时返回NULL（表示空节点）
• 否则创建新节点，并将当前字符赋给节点值
• 递归构建左子树和右子树
• 每次递归调用后count会递增

中序遍历函数

void Inorder(TreeNode* root)
{
    if(root==NULL)
    {
        return;
    }
    Inorder(root->left);
    printf("%c ",root->val);
    Inorder(root->right);
}

实现标准的二叉树中序遍历：

1. 递归遍历左子树
2. 访问当前节点（打印节点值）
3. 递归遍历右子树

主函数

int main()
{
    char arr[101];
    scanf("%s",arr);
    int count = 0;
    TreeNode* tree = maketree(arr,&count);
    Inorder(tree);
    return 0;
}

主程序流程：

• 读取最多100个字符的输入字符串
• 初始化计数器count为0
• 调用maketree构建二叉树
• 调用Inorder进行中序遍历输出

输入输出示例

假设输入字符串为"ABD##E##C##"（其中#表示空节点），构建的二叉树结构为：

    A
   / \
  B   C
 / \
D   E

中序遍历输出为：D B E A C