4.2 阻抗和导纳矩阵
上一节介绍了如何才能定义TEM波和非TEM波的等效电压和电流。确定网络中不同点的电压和电流后,就可利用电路理论的阻抗和/或导纳矩阵把这些端点量或"端口"量联系起来,进而使用矩阵来描述网络。这种表述可用来开发任意网络的等效电路,在讨论无源元件如耦合器和滤波器的设计时,这种等效电路表述非常有用(端口一词是在20世纪50年代由H.A.Wheeler引入的,目的是取代表述不清的术语"两端点对"[2,3])。
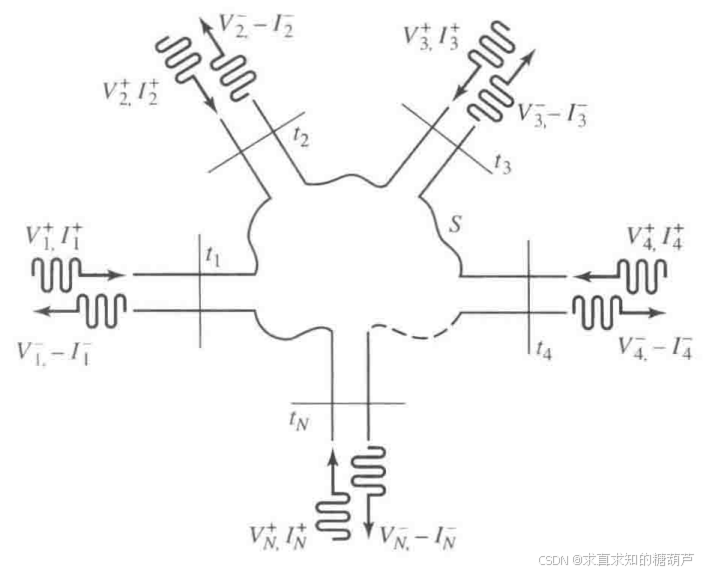
图4.5任意N端口微波网络
下面从如图4.5所示的任意N端口微波网络开始。图4.5中的端口可以是某种形式的传输线或单一波导传播模的等效传输线。若网络的物理端口之一是支持多个传播模的波导,则可为这些模考虑添加其他的电端口,每个"电端口"对应一个模式,有自己独立的等效电压、电流和等效传输线。
对于通用端口进行分析,我们在第n个端口上的一个指定点处,**定义了一个端平面 t n t_{n} tn,并定义了等效的入射波电压和电流( V n + , I n + V_{n}^{+},I_{n}^{+} Vn+,In+)及等效的反射波电压和电流( V n − , I n − V_{n}^{-},I_{n}^{-} Vn−,In−)。**在为电压和电流相量提供相位参考时,这些端平面的作用很重要。下面给出第n个端平面上的总电压和电流:
V n = V n + + V n − ( 4.24 a ) V_{n}=V_{n}^{+}+V_{n}^{-} \quad (4.24a) Vn=Vn++Vn−(4.24a)
I n = I n + − I n − ( 4.24 b ) I_{n}=I_{n}^{+}-I_{n}^{-} \quad (4.24b) In=In+−In−(4.24b)
这与式(4.8)在 z = 0 z=0 z=0时得到的结果相同。
微波网络的阻抗矩阵Z把这些电压和电流联系起来:
V 1 V 2 ⋮ V N \] = \[ Z 11 Z 12 ⋯ Z 1 N Z 21 Z 22 ⋯ Z 2 N ⋮ ⋮ ⋱ ⋮ Z N 1 Z N 2 ⋯ Z N N \] \[ I 1 I 2 ⋮ I N \] \\begin{bmatrix}V_1 \\\\V_2 \\\\\\vdots \\\\V_N\\end{bmatrix}=\\begin{bmatrix}Z_{11}\&Z_{12}\&\\cdots \&Z_{1N}\\\\Z_{21}\&Z_{22}\&\\cdots \&Z_{2N}\\\\\\vdots\&\\vdots\&\\ddots\&\\vdots\\\\Z_{N1}\&Z_{N2}\&\\cdots \&Z_{NN}\\end{bmatrix}\\begin{bmatrix}I_1 \\\\I_2 \\\\\\vdots\\\\I_N\\end{bmatrix} V1V2⋮VN = Z11Z21⋮ZN1Z12Z22⋮ZN2⋯⋯⋱⋯Z1NZ2N⋮ZNN I1I2⋮IN 或以矩阵形式写为 V = Z I ( 4.25 ) V=ZI\\quad(4.25) V=ZI(4.25) 类似地,可以将导纳矩阵Y定义为 \[ I 1 I 2 ⋮ I N \] = \[ Y 11 Y 12 ⋯ Y 1 N Y 21 Y 22 ⋯ Y 2 N ⋮ ⋮ ⋱ ⋮ Y N 1 Y N 2 ⋯ Y N N \] \[ V 1 V 2 ⋮ V N \] \\begin{bmatrix}I_1\\\\I_2\\\\\\vdots\\\\I_N\\end{bmatrix}=\\begin{bmatrix}Y_{11}\&Y_{12}\&\\cdots \&Y_{1N}\\\\Y_{21}\&Y_{22}\&\\cdots \&Y_{2N}\\\\\\vdots\&\\vdots\&\\ddots\&\\vdots\\\\Y_{N1}\&Y_{N2}\&\\cdots \&Y_{NN}\\end{bmatrix}\\begin{bmatrix}V_1\\\\V_2\\\\\\vdots\\\\V_N\\end{bmatrix} I1I2⋮IN = Y11Y21⋮YN1Y12Y22⋮YN2⋯⋯⋱⋯Y1NY2N⋮YNN V1V2⋮VN 或以矩阵形式写为 I = Y V ( 4.26 ) I=YV\\quad(4.26) I=YV(4.26) 显然,Z矩阵和Y矩阵互为逆矩阵: Y = Z − 1 ( 4.27 ) Y=Z\^{-1}\\quad(4.27) Y=Z−1(4.27) 注意,Z矩阵和Y矩阵把所有端口电压和电流联系起来了。 由式(4.25)可知 Z i j Z_{ij} Zij为 Z i j = V i I j ∣ I k = 0 , k ≠ j ( 4.28 ) Z_{ij}=\\left.\\frac{V_{i}}{I_{j}}\\right\|_{I_{k}=0,\\quad k\\neq j}\\quad(4.28) Zij=IjVi Ik=0,k=j(4.28) 换言之,式(4.28)说明 Z i j Z_{ij} Zij可以通过激励电流为 I j I_{j} Ij的端口j,而其他所有端口开路(故有 I k = 0 , k ≠ j I_{k}=0,\\quad k\\neq j Ik=0,k=j)并测量端口i的开路电压得出。这样,当所有的其他端口开路时, Z i i Z_{ii} Zii是向端口i往里看的输入阻抗,而当所有其他端口开路时, Z i j Z_{ij} Zij是端口i和j之间的传输阻抗。  **以上图所示的一个二端口网络为例,** U ˙ 1 = z 11 I ˙ 1 + z 12 I ˙ 2 U ˙ 2 = z 21 I ˙ 1 + z 22 I ˙ 2 \\dot{U}_1 = z_{11} \\dot{I}_1 + z_{12} \\dot{I}_2 \\\\ \\dot{U}_2 = z_{21} \\dot{I}_1 + z_{22} \\dot{I}_2 U˙1=z11I˙1+z12I˙2U˙2=z21I˙1+z22I˙2 我们想求 z 11 z_{11} z11即令 I ˙ 2 = 0 求 U ˙ 1 I ˙ 1 \\dot{I}_2=0求\\dfrac{\\dot{U}_{1}}{\\dot{I}_{1}} I˙2=0求I˙1U˙1。同理想求 z 21 z_{21} z21即令 I ˙ 2 = 0 求 U ˙ 2 I ˙ 1 \\dot{I}_2=0求\\dfrac{\\dot{U}_{2}}{\\dot{I}_{1}} I˙2=0求I˙1U˙2 类似地,由式(4.26)可知 Y i j Y_{ij} Yij为 Y i j = I i V j ∣ V k = 0 , k ≠ j ( 4.29 ) Y_{ij}=\\left.\\frac{I_{i}}{V_{j}}\\right\|_{V_{k}=0,\\quad k\\neq j}\\quad(4.29) Yij=VjIi Vk=0,k=j(4.29) 这说明当所有其他端口短路时(有 V k = 0 V_{k}=0 Vk=0, k ≠ j k\\neq j k=j), Y i j Y_{ij} Yij可通过激励电压为 V j V_{j} Vj的端口j并测量端口i的短路电流来得到。 一般来说,每个矩阵元素 Z i j Z_{ij} Zij或 Y i j Y_{ij} Yij都能是复数。对于任意N端口网络,阻抗和导纳是 N × N N\\times N N×N矩阵,因此有 2 N 2 2N\^{2} 2N2个自变量或自由度。然而,在实际中,很多网络要么是互易的,要么是无耗的,要么既是互易的又是无耗的。若网络是**互易的(即不含非互易性媒质,如铁氧体、等离子体或有源器件)**,则可以证明阻抗和导纳矩阵是**对称的,有 Z i j = Z j i Z_{ij}=Z_{ji} Zij=Zji和 Y i j = Y j i Y_{ij}=Y_{ji} Yij=Yji**;若网络是**无耗的**,则可以证明**所有矩阵元素 Z i j Z_{ij} Zij或 Y i j Y_{ij} Yij是纯虚数**。这些特定情况中的任何一种都会减少N端口网络应有的自变量数或自由度数。推导如下: #### 4.2.1 互易网络 ##### 互易定理 互易性是物理学和很多工程领域中的一个普遍概念,读者也许已经熟悉电路理论的互易定理。这里将导出两种不同形式的电磁场的洛伦兹互易定理。本书稍后将利用该定理来得到代表微波电路的网络矩阵的一般特性,计算波导与电流探针和电流环的耦合,计算波导间通过小孔的耦合。这种非常有用的概念还具有其他重要应用。 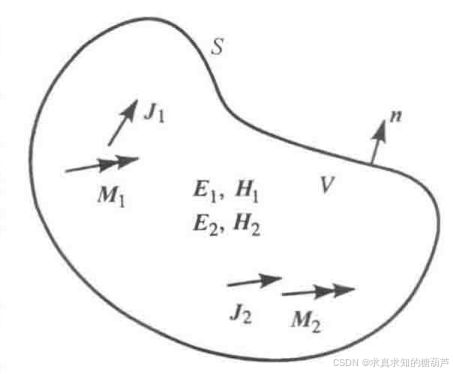 图1.15洛伦兹互易定理示意图 考虑由封闭表面 S S S围成的体积 V V V内的两组分开的源 J 1 \\boldsymbol{J}_{1} J1、 M 1 \\boldsymbol{M}_{1} M1和 J 2 \\boldsymbol{J}_{2} J2、 M 2 \\boldsymbol{M}_{2} M2,它们产生的场分别为 E 1 \\boldsymbol{E}_{1} E1、 H 1 \\boldsymbol{H}_{1} H1和 E 2 \\boldsymbol{E}_{2} E2、 H 2 \\boldsymbol{H}_{2} H2,如图1.15所示。两组源和场分别满足麦克斯韦方程组,所以可以写出 ∇ × E 1 = − j ω μ H 1 − M 1 ( 1.152 a ) \\nabla \\times \\boldsymbol{E}_{1} = -j \\omega \\mu \\boldsymbol{H}_{1} - \\boldsymbol{M}_{1} \\quad (1.152a) ∇×E1=−jωμH1−M1(1.152a) ∇ × H 1 = j ω ϵ E 1 + J 1 ( 1.152 b ) \\nabla \\times \\boldsymbol{H}_{1} = j \\omega \\epsilon \\boldsymbol{E}_{1} + \\boldsymbol{J}_{1} \\quad (1.152b) ∇×H1=jωϵE1+J1(1.152b) ∇ × E 2 = − j ω μ H 2 − M 2 ( 1.153 a ) \\nabla \\times \\boldsymbol{E}_{2} = -j \\omega \\mu \\boldsymbol{H}_{2} - \\boldsymbol{M}_{2} \\quad (1.153a) ∇×E2=−jωμH2−M2(1.153a) ∇ × H 2 = j ω ϵ E 2 + J 2 ( 1.153 b ) \\nabla \\times \\boldsymbol{H}_{2} = j \\omega \\epsilon \\boldsymbol{E}_{2} + \\boldsymbol{J}_{2} \\quad (1.153b) ∇×H2=jωϵE2+J2(1.153b) **图1.15 洛伦兹互易定理示意图** 现在考虑量 ∇ ⋅ ( E 1 × H 2 − E 2 × H 1 ) \\nabla \\cdot (\\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 - \\boldsymbol{E}_2 \\times \\boldsymbol{H}_1) ∇⋅(E1×H2−E2×H1),它可以由向量恒等式(B.8)展开得到: ∇ ⋅ ( E 1 × H 2 − E 2 × H 1 ) = J 1 ⋅ E 2 − J 2 ⋅ E 1 + M 2 ⋅ H 1 − M 1 ⋅ H 2 ( 1.154 ) \\nabla \\cdot (\\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 - \\boldsymbol{E}_2 \\times \\boldsymbol{H}_1) = \\boldsymbol{J}_1 \\cdot \\boldsymbol{E}_2 - \\boldsymbol{J}_2 \\cdot \\boldsymbol{E}_1 + \\boldsymbol{M}_2 \\cdot \\boldsymbol{H}_1 - \\boldsymbol{M}_1 \\cdot \\boldsymbol{H}_2 \\quad (1.154) ∇⋅(E1×H2−E2×H1)=J1⋅E2−J2⋅E1+M2⋅H1−M1⋅H2(1.154) 在整个体积 V V V内积分,并利用散度定理(B.15),可得 ∫ V ∇ ⋅ ( E 1 × H 2 − E 2 × H 1 ) d v = ∮ S ( E 1 × H 2 − E 2 × H 1 ) ⋅ d s = ∫ V ( E 2 ⋅ J 1 − E 1 ⋅ J 2 + H 1 ⋅ M 2 − H 2 ⋅ M 1 ) d v ( 1.155 ) \\begin{aligned} \\int_{V} \\nabla \\cdot (\\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 - \\boldsymbol{E}_2 \\times \\boldsymbol{H}_1) \\, \\mathrm{d} v \&= \\oint_{S} (\\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 - \\boldsymbol{E}_2 \\times \\boldsymbol{H}_1) \\cdot \\mathrm{d} \\boldsymbol{s} \\\\ \&= \\int_{V} (\\boldsymbol{E}_2 \\cdot \\boldsymbol{J}_1 - \\boldsymbol{E}_1 \\cdot \\boldsymbol{J}_2 + \\boldsymbol{H}_1 \\cdot \\boldsymbol{M}_2 - \\boldsymbol{H}_2 \\cdot \\boldsymbol{M}_1) \\, \\mathrm{d} v \\end{aligned} \\quad (1.155) ∫V∇⋅(E1×H2−E2×H1)dv=∮S(E1×H2−E2×H1)⋅ds=∫V(E2⋅J1−E1⋅J2+H1⋅M2−H2⋅M1)dv(1.155) 式(1.155)是互易定理的普遍形式,但实际上有些特殊情况往往会导致一些简化。考虑三种情况。 **S S S封闭无源。** 这时 J 1 = J 2 = M 1 = M 2 = 0 \\boldsymbol{J}_1 = \\boldsymbol{J}_2 = \\boldsymbol{M}_1 = \\boldsymbol{M}_2 = 0 J1=J2=M1=M2=0,场 E 1 \\boldsymbol{E}_1 E1, H 1 \\boldsymbol{H}_1 H1和 E 2 \\boldsymbol{E}_2 E2, H 2 \\boldsymbol{H}_2 H2为无源场。此时,式(1.155)的右边为零,于是得到 ∮ S E 1 × H 2 ⋅ d s = ∮ S E 2 × H 1 ⋅ d s ( 1.156 ) \\oint_{S} \\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 \\cdot \\mathrm{d} \\boldsymbol{s} = \\oint_{S} \\boldsymbol{E}_2 \\times \\boldsymbol{H}_1 \\cdot \\mathrm{d} \\boldsymbol{s} \\quad (1.156) ∮SE1×H2⋅ds=∮SE2×H1⋅ds(1.156) 这个结果将在第4章用来阐明互易微波网络的阻抗矩阵的对称性。 **S S S为理想导体。** 例如, S S S可能是一个理想导电的封闭腔的内表面。于是式(1.155)的面积分为零,因为 E 1 × H 2 ⋅ n = ( n × E 1 ) ⋅ H 2 \\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 \\cdot \\boldsymbol{n} = (\\boldsymbol{n} \\times \\boldsymbol{E}_1) \\cdot \\boldsymbol{H}_2 E1×H2⋅n=(n×E1)⋅H2\[由向量恒等式(B.3)得到\],而 n × E 1 \\boldsymbol{n} \\times \\boldsymbol{E}_1 n×E1在理想导体表面为零( E 2 \\boldsymbol{E}_2 E2也类似)。结果为 ∫ V ( E 1 ⋅ J 2 − H 1 ⋅ M 2 ) d v = ∫ V ( E 2 ⋅ J 1 − H 2 ⋅ M 1 ) d v ( 1.157 ) \\int_{V} (\\boldsymbol{E}_1 \\cdot \\boldsymbol{J}_2 - \\boldsymbol{H}_1 \\cdot \\boldsymbol{M}_2) \\, \\mathrm{d} v = \\int_{V} (\\boldsymbol{E}_2 \\cdot \\boldsymbol{J}_1 - \\boldsymbol{H}_2 \\cdot \\boldsymbol{M}_1) \\, \\mathrm{d} v \\quad (1.157) ∫V(E1⋅J2−H1⋅M2)dv=∫V(E2⋅J1−H2⋅M1)dv(1.157) 这个结果与电路理论的互易定理相似。换言之,这个结果说,系统的响应 E 1 \\boldsymbol{E}_1 E1, E 2 \\boldsymbol{E}_2 E2不会因为源点和场点的交换而改变,即由 J 2 \\boldsymbol{J}_2 J2产生的在 J 1 \\boldsymbol{J}_1 J1处的场 E 2 \\boldsymbol{E}_2 E2与由 J 1 \\boldsymbol{J}_1 J1产生的在 J 2 \\boldsymbol{J}_2 J2处的场 E 1 \\boldsymbol{E}_1 E1相等。 **S S S为无限远处的球面。** 此时, S S S处的场极其远离源,因而可以局部地考虑为平面波。于是,将阻抗关系 H = n × E / η \\boldsymbol{H} = \\boldsymbol{n} \\times \\boldsymbol{E} / \\eta H=n×E/η应用到式(1.155)可得 ( E 1 × H 2 − E 2 × H 1 ) ⋅ n = ( n × E 1 ) ⋅ H 2 − ( n × E 2 ) ⋅ H 1 = 1 η H 1 ⋅ H 2 − 1 η H 2 ⋅ H 1 = 0 (\\boldsymbol{E}_1 \\times \\boldsymbol{H}_2 - \\boldsymbol{E}_2 \\times \\boldsymbol{H}_1) \\cdot \\boldsymbol{n} = (\\boldsymbol{n} \\times \\boldsymbol{E}_1) \\cdot \\boldsymbol{H}_2 - (\\boldsymbol{n} \\times \\boldsymbol{E}_2) \\cdot \\boldsymbol{H}_1 = \\frac{1}{\\eta} \\boldsymbol{H}_1 \\cdot \\boldsymbol{H}_2 - \\frac{1}{\\eta} \\boldsymbol{H}_2 \\cdot \\boldsymbol{H}_1 = 0 (E1×H2−E2×H1)⋅n=(n×E1)⋅H2−(n×E2)⋅H1=η1H1⋅H2−η1H2⋅H1=0 所以再次得到了式(1.157)的结果。对于表面阻抗边界条件成立的封闭表面 S S S的情况,也能得到这个结果。 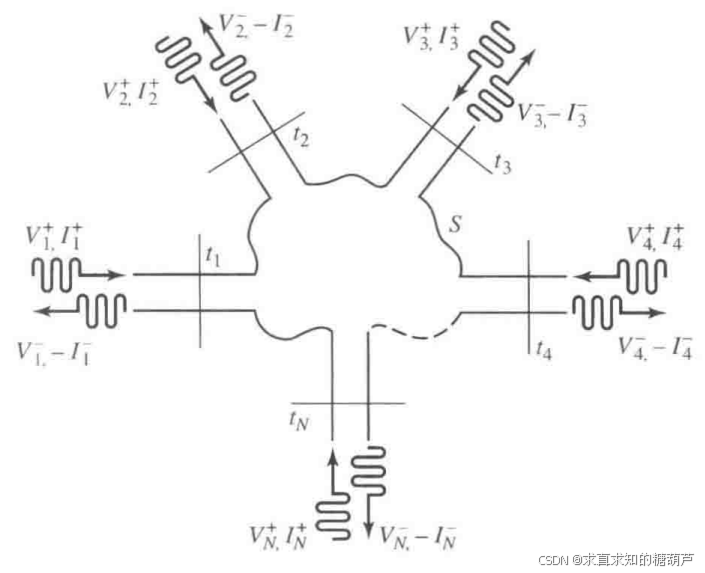 图4.5所示的任意网络是互易的(无有源器件、铁氧体或等离子体), **推导中除端口1和端口2外,其他所有端平面上都设置为短路**。仅在**端口1** 施加外部激励a,网络内部会建立起一套稳定的电磁场分布,记为 ( E a , H a ) (\\mathbf{E}_a, \\mathbf{H}_a) (Ea,Ha)。仅在**端口2** 施加另一个**独立** 的外部激励b。网络内部建立起另一套场分布,记为 ( E b , H b ) (\\mathbf{E}_b, \\mathbf{H}_b) (Eb,Hb)。在每种状态下,网络内部**都没有产生场的、独立的物理源** 。场是由**边界条件** (端口1或2的激励,以及其他端口的短路条件)决定的。因此,对于每一套场,它们在曲面S包围的体积V内都满足**无源的、齐次的** 麦克斯韦方程组。现在网络有场 E a E_{a} Ea, H a H_{a} Ha和 E b E_{b} Eb, H b H_{b} Hb,它们是由来自网络外部的两个独立源a和b产生的。因此,式(1.156)的互易定理表明 ∮ S E a × H b ⋅ d s = ∮ S E b × H a ⋅ d s ( 4.30 ) \\oint_{S} E_{a} \\times H_{b} \\cdot \\mathrm{d} s = \\oint_{S} E_{b} \\times H_{a} \\cdot \\mathrm{d} s \\quad (4.30) ∮SEa×Hb⋅ds=∮SEb×Ha⋅ds(4.30) 式中,S是沿网络边界并过所有端口的端平面的封闭曲面。若网络和传输线的边界壁是**金属** ,则在**壁上有 E tan = 0 E_{\\text{tan}} = 0 Etan=0(假设是理想导体)** 。若网络或传输线是开放性结构,如微带或槽线,则可把边界设置在离线足够远的位置,使得 E tan E_{\\text{tan}} Etan可以忽略不计。这样,式(4.30)的积分的非零贡献就只来自端口1和端口2的截面积。 > 在理想导体表面,切向电场必须为零,这是电磁场的边界条件。即 E tan = 0 E_{\\text{tan}} = 0 Etan=0。 > > 被积函数 E × H ⋅ d s E \\times H \\cdot ds E×H⋅ds 中, d s ds ds 的方向是曲面的外法向。利用矢量恒等式,该项等于 ( E × H ) ⋅ n \^ = ( n \^ × E ) ⋅ H (E \\times H) \\cdot \\hat{n} = (\\hat{n} \\times E) \\cdot H (E×H)⋅n\^=(n\^×E)⋅H。由于 n \^ × E = n \^ × E tan \\hat{n} \\times E=\\hat{n} \\times E_{\\text{tan}} n\^×E=n\^×Etan,因此在理想导体壁上,该项为零。**所以,网络金属外壳对式(4.30)的面积分没有贡献。** > > 对于微带线、共面波导等开放式结构,没有封闭的金属外壳。我们可以**人为设定一个边界** ,这个边界距离导带足够远。在远离导带的地方,电磁场强度衰减到非常微弱, E tan E_{\\text{tan}} Etan 近似为零。因此,这部分边界对积分的贡献也可以忽略。 > > **除了端口1和端口2,其他所有端口都被"短路"处理** 。短路意味着在该端口端平面上强制 V = 0 V=0 V=0,这等价于该处的横向电场 E t a n = 0 E_{tan} = 0 Etan=0。因此,**短路端口端面的积分贡献也为零** 。最终,整个封闭曲面S上,**只有端口1和端口2的端平面**对式(4.30)的积分有非零贡献。 由4.1节可知,源a和b产生的场可在端平面 t 1 t_{1} t1和 t 2 t_{2} t2上算出: E 1 a = V 1 a e 1 , H 1 a = I 1 a h 1 E 1 b = V 1 b e 1 , H 1 b = I 1 b h 1 E 2 a = V 2 a e 2 , H 2 a = I 2 a h 2 E 2 b = V 2 b e 2 , H 2 b = I 2 b h 2 ( 4.31 ) \\begin{aligned}E_{1a} = V_{1a} e_{1}, \\quad H_{1a} = I_{1a} h_{1} \\\\ E_{1b} = V_{1b} e_{1}, \\quad H_{1b} = I_{1b} h_{1} \\\\ E_{2a} = V_{2a} e_{2}, \\quad H_{2a} = I_{2a} h_{2}\\\\ E_{2b} = V_{2b} e_{2}, \\quad H_{2b} = I_{2b} h_{2} \\end{aligned}\\quad(4.31) E1a=V1ae1,H1a=I1ah1E1b=V1be1,H1b=I1bh1E2a=V2ae2,H2a=I2ah2E2b=V2be2,H2b=I2bh2(4.31) 式中, e 1 e_{1} e1, h 1 h_{1} h1和 e 2 e_{2} e2, h 2 h_{2} h2分别是端口1和端口2的横模场,而V和I是等效的总电压和电流(如 E 1 b E_{1b} E1b是源b在端口1的端平面 t 1 t_{1} t1上产生的横电场)。 > **小结一下:** 对于非TEM传输线(如波导),其横截面上的**横向电磁场** ( E t , H t ) (E_t, H_t) (Et,Ht) 可以分解为两部分: > > **模式分布函数** e ( x , y ) e(x, y) e(x,y) 和 h ( x , y ) h(x, y) h(x,y):描述了场在横截面上的固定形状,与传播方向(z)和幅度无关。它们满足关系 h = ( z \^ × e ) / Z w h = (\\hat{z} \\times e) / Z_w h=(z\^×e)/Zw,其中 Z w Z_w Zw 是该模式的波阻抗。 > > **等效电路量** V ( z ) V(z) V(z) 和 I ( z ) I(z) I(z):描述了场沿传播方向的幅度和相位变化,它们的行为与传输线上的电压波、电流波完全一致。 > > 参考面处设 z = 0 z=0 z=0,带入(4.15) 具体关系为,: > E t ( x , y , z ) = V ( z ) ⋅ e ( x , y ) H t ( x , y , z ) = I ( z ) ⋅ h ( x , y ) E_t(x,y,z) = V(z) \\cdot e(x,y)\\\\H_t(x,y,z) = I(z) \\cdot h(x,y) Et(x,y,z)=V(z)⋅e(x,y)Ht(x,y,z)=I(z)⋅h(x,y) > > 通过**功率归一化** (4.10),使得 ∫ S e × h ⋅ z \^ d s = 1 \\int_S e \\times h \\cdot \\hat{z} \\, ds = 1 ∫Se×h⋅z\^ds=1,从而有**传输的复功率** 等于 1 2 V I ∗ \\frac{1}{2} V I\^\* 21VI∗。这让 V V V 和 I I I 成为等效电压和电流。 > > 在互易性证明中,我们有两种独立的激励状态(分别对应"源a"和"源b")。 > > 对于**第一种激励状态(a)** :它在端口1的端面 t 1 t_1 t1 上,产生了特定的横向场。根据4.1节理论,这个场可以写成: E 1 a = V 1 a e 1 E_{1a} = V_{1a} e_1 E1a=V1ae1, H 1 a = I 1 a h 1 H_{1a} = I_{1a} h_1 H1a=I1ah1。这里 V 1 a V_{1a} V1a 和 I 1 a I_{1a} I1a 就是在状态a下,**端口1的总等效电压和总等效电流** **(即入射波与反射波之和)**。同时,状态a也会在端口2的端面 t 2 t_2 t2 上感应出场,同理可写为: E 2 a = V 2 a e 2 E_{2a} = V_{2a} e_2 E2a=V2ae2, H 2 a = I 2 a h 2 H_{2a} = I_{2a} h_2 H2a=I2ah2。 V 2 a V_{2a} V2a 和 I 2 a I_{2a} I2a 是状态a下端口2的总等效电压和电流。对于**第二种激励状态(b)** ,同理,下标换为"b"。**无论激励源如何,端口本身的横向模式分布 e n , h n e_n, h_n en,hn 是固定不变的** ,它只由端口的几何结构和传播的模式决定。**变化的是反映激励状态和网络响应的系数 V V V 和 I I I**。通过对网络边界(理想导体壁或远处边界)和短路端口端面上切向电场为零的分析,将式(4.30)的全封闭面积分,简化为仅在**所研究的两个端口(1和2)端面上** 的积分。借助**4.1节** 建立的、将横向电磁场分解为**固定模式分布** ( e , h ) (e, h) (e,h) 与**等效电路量** ( V , I ) (V, I) (V,I) 相乘的理论框架,将端口端面上的场 E , H E, H E,H 用等效电压 V V V 和电流 I I I 表示出来(式4.31)**从而完成了场-路转换**。将式(4.31)代入简化后的式(4.30),利用模式函数的归一化条件,积分运算就转化为了关于 V 1 a , I 1 b , V 1 b , I 1 a V_{1a}, I_{1b}, V_{1b}, I_{1a} V1a,I1b,V1b,I1a 等电路量的代数运算,最终可以推导出网络参数的互易性质( Y 12 = Y 21 Y_{12} = Y_{21} Y12=Y21)。 在端口1的端平面 S 1 S_1 S1上,面积分贡献为 ∫ S 1 ( E a × H b − E b × H a ) ⋅ d s = 0. \\int_{S_1} (\\boldsymbol{E}_a \\times \\boldsymbol{H}_b - \\boldsymbol{E}_b \\times \\boldsymbol{H}_a) \\cdot \\mathrm{d}\\boldsymbol{s}=0. ∫S1(Ea×Hb−Eb×Ha)⋅ds=0. 利用式(4.31)的表达式: E a = V 1 a e 1 , H b = I 1 b h 1 , E b = V 1 b e 1 , H a = I 1 a h 1 , \\boldsymbol{E}_a = V_{1a} \\boldsymbol{e}_1, \\quad \\boldsymbol{H}_b = I_{1b} \\boldsymbol{h}_1, \\quad \\boldsymbol{E}_b = V_{1b} \\boldsymbol{e}_1, \\quad \\boldsymbol{H}_a = I_{1a} \\boldsymbol{h}_1, Ea=V1ae1,Hb=I1bh1,Eb=V1be1,Ha=I1ah1, 代入得 E a × H b = V 1 a I 1 b ( e 1 × h 1 ) , E b × H a = V 1 b I 1 a ( e 1 × h 1 ) . \\boldsymbol{E}_a \\times \\boldsymbol{H}_b = V_{1a} I_{1b} (\\boldsymbol{e}_1 \\times \\boldsymbol{h}_1), \\quad \\boldsymbol{E}_b \\times \\boldsymbol{H}_a = V_{1b} I_{1a} (\\boldsymbol{e}_1 \\times \\boldsymbol{h}_1). Ea×Hb=V1aI1b(e1×h1),Eb×Ha=V1bI1a(e1×h1). 因此, E a × H b − E b × H a = ( V 1 a I 1 b − V 1 b I 1 a ) ( e 1 × h 1 ) . \\boldsymbol{E}_a \\times \\boldsymbol{H}_b - \\boldsymbol{E}_b \\times \\boldsymbol{H}_a = (V_{1a} I_{1b} - V_{1b} I_{1a}) (\\boldsymbol{e}_1 \\times \\boldsymbol{h}_1). Ea×Hb−Eb×Ha=(V1aI1b−V1bI1a)(e1×h1). 点乘面积元 d s = n \^ 1 d s \\mathrm{d}\\boldsymbol{s} = \\hat{n}_1 \\mathrm{d}s ds=n\^1ds(其中 n \^ 1 \\hat{n}_1 n\^1 是 S 1 S_1 S1 的法向单位矢量,指向网络内部),并在 S 1 S_1 S1上积分: ∫ S 1 ( E a × H b − E b × H a ) ⋅ d s = ( V 1 a I 1 b − V 1 b I 1 a ) ∫ S 1 e 1 × h 1 ⋅ n \^ 1 d s = 0. \\int_{S_1} (\\boldsymbol{E}_a \\times \\boldsymbol{H}_b - \\boldsymbol{E}_b \\times \\boldsymbol{H}_a) \\cdot \\mathrm{d}\\boldsymbol{s} = (V_{1a} I_{1b} - V_{1b} I_{1a}) \\int_{S_1} \\boldsymbol{e}_1 \\times \\boldsymbol{h}_1 \\cdot \\hat{n}_1 \\mathrm{d}s=0. ∫S1(Ea×Hb−Eb×Ha)⋅ds=(V1aI1b−V1bI1a)∫S1e1×h1⋅n\^1ds=0. 记 d s = n \^ 1 d s \\mathrm{d}\\boldsymbol{s} = \\hat{n}_1 \\mathrm{d}s ds=n\^1ds,该积分可写为 ( V 1 a I 1 b − V 1 b I 1 a ) ∫ S 1 e 1 × h 1 ⋅ d s = 0. (V_{1a} I_{1b} - V_{1b} I_{1a}) \\int_{S_1} \\boldsymbol{e}_1 \\times \\boldsymbol{h}_1 \\cdot \\mathrm{d}\\boldsymbol{s}=0. (V1aI1b−V1bI1a)∫S1e1×h1⋅ds=0. 同理,在端口2的端平面 S 2 S_2 S2 上,有 ∫ S 2 ( E a × H b − E b × H a ) ⋅ d s = ( V 2 a I 2 b − V 2 b I 2 a ) ∫ S 2 e 2 × h 2 ⋅ d s = 0. \\int_{S_2} (\\boldsymbol{E}_a \\times \\boldsymbol{H}_b - \\boldsymbol{E}_b \\times \\boldsymbol{H}_a) \\cdot \\mathrm{d}\\boldsymbol{s} = (V_{2a} I_{2b} - V_{2b} I_{2a}) \\int_{S_2} \\boldsymbol{e}_2 \\times \\boldsymbol{h}_2 \\cdot \\mathrm{d}\\boldsymbol{s}=0. ∫S2(Ea×Hb−Eb×Ha)⋅ds=(V2aI2b−V2bI2a)∫S2e2×h2⋅ds=0. 将两端口贡献相加,可得 ( V 1 a I 1 b − V 1 b I 1 a ) ∫ S 1 e 1 × h 1 ⋅ d s + ( V 2 a I 2 b − V 2 b I 2 a ) ∫ S 2 e 2 × h 2 ⋅ d s = 0 ( 4.32 ) (V_{1a} I_{1b} - V_{1b} I_{1a}) \\int_{S_{1}} e_{1} \\times h_{1} \\cdot \\mathrm{d} s + (V_{2a} I_{2b} - V_{2b} I_{2a}) \\int_{S_{2}} e_{2} \\times h_{2} \\cdot \\mathrm{d} s = 0 \\quad (4.32) (V1aI1b−V1bI1a)∫S1e1×h1⋅ds+(V2aI2b−V2bI2a)∫S2e2×h2⋅ds=0(4.32) 式中, S 1 S_{1} S1和 S 2 S_{2} S2是端口1和端口2的端平面上的截面积。 如在4.1节中那样,等效电压和电流是这样来定义的:使得通过给定端口的功率可用 V I ∗ / 2 V I\^{\*} / 2 VI∗/2来表示;然后比较式(4.31)与式(4.6) ( z = 0 ) (z=0) (z=0),表明对每个端口有 C 1 = C 2 = 1 C_{1} = C_{2} = 1 C1=C2=1,所以 E t ( x , y , z ) = e ( x , y ) ( A + e − j β z + A − e j β z ) = e ( x , y ) C 1 ( V + e − j β z + V − e j β z ) ( 4.6 a ) H t ( x , y , z ) = h ( x , y ) ( A + e − j β z − A − e j β z ) = h ( x , y ) C 2 ( I + e − j β z − I − e j β z ) ( 4.6 b ) E_{t}(x, y, z)=e(x, y)\\left(A\^{+} \\mathrm{e}\^{-\\mathrm{j} \\beta z}+A\^{-} \\mathrm{e}\^{\\mathrm{j} \\beta z}\\right)=\\frac{e(x, y)}{C_{1}}\\left(V\^{+} \\mathrm{e}\^{-\\mathrm{j} \\beta z}+V\^{-} \\mathrm{e}\^{\\mathrm{j} \\beta z}\\right)\\quad(4.6a) \\\\H_{t}(x, y, z)=h(x, y)\\left(A\^{+} \\mathrm{e}\^{-\\mathrm{j} \\beta z}-A\^{-} \\mathrm{e}\^{\\mathrm{j} \\beta z}\\right)=\\frac{h(x, y)}{C_{2}}\\left(I\^{+} \\mathrm{e}\^{-\\mathrm{j} \\beta z}-I\^{-} \\mathrm{e}\^{\\mathrm{j} \\beta z}\\right)\\quad(4.6b) Et(x,y,z)=e(x,y)(A+e−jβz+A−ejβz)=C1e(x,y)(V+e−jβz+V−ejβz)(4.6a)Ht(x,y,z)=h(x,y)(A+e−jβz−A−ejβz)=C2h(x,y)(I+e−jβz−I−ejβz)(4.6b) ∫ S 1 e 1 × h 1 ⋅ d s = ∫ S 2 e 2 × h 2 ⋅ d s = 1 ( 4.33 ) \\int_{S_{1}} e_{1} \\times h_{1} \\cdot \\mathrm{d} s = \\int_{S_{2}} e_{2} \\times h_{2} \\cdot \\mathrm{d} s = 1 \\quad (4.33) ∫S1e1×h1⋅ds=∫S2e2×h2⋅ds=1(4.33) 这会将式(4.32)简化为 V 1 a I 1 b − V 1 b I 1 a + V 2 a I 2 b − V 2 b I 2 a = 0 ( 4.34 ) V_{1a} I_{1b} - V_{1b} I_{1a} + V_{2a} I_{2b} - V_{2b} I_{2a} = 0 \\quad (4.34) V1aI1b−V1bI1a+V2aI2b−V2bI2a=0(4.34) 现在利用该二端口网络的 2 × 2 2 \\times 2 2×2导纳矩阵 I 1 = Y 11 V 1 + Y 12 V 2 I 2 = Y 21 V 1 + Y 22 V 2 I_{1} = Y_{11} V_{1} + Y_{12} V_{2}\\\\ I_{2} = Y_{21} V_{1} + Y_{22} V_{2} I1=Y11V1+Y12V2I2=Y21V1+Y22V2 来消去I项。代入式(4.34)可得 对于状态 a a a,有: I 1 a = Y 11 V 1 a + Y 12 V 2 a , I 2 a = Y 21 V 1 a + Y 22 V 2 a . \\begin{aligned} I_{1a} \&= Y_{11} V_{1a} + Y_{12} V_{2a}, \\\\ I_{2a} \&= Y_{21} V_{1a} + Y_{22} V_{2a}. \\end{aligned} I1aI2a=Y11V1a+Y12V2a,=Y21V1a+Y22V2a. 对于状态 b b b,有: I 1 b = Y 11 V 1 b + Y 12 V 2 b , I 2 b = Y 21 V 1 b + Y 22 V 2 b . \\begin{aligned} I_{1b} \&= Y_{11} V_{1b} + Y_{12} V_{2b}, \\\\ I_{2b} \&= Y_{21} V_{1b} + Y_{22} V_{2b}. \\end{aligned} I1bI2b=Y11V1b+Y12V2b,=Y21V1b+Y22V2b. 将以上表达式代入式(4.34): V 1 a I 1 b − V 1 b I 1 a + V 2 a I 2 b − V 2 b I 2 a = Y 11 V 1 a V 1 b + Y 12 V 1 a V 2 b − Y 11 V 1 b V 1 a − Y 12 V 1 b V 2 a + Y 21 V 2 a V 1 b + Y 22 V 2 a V 2 b − Y 21 V 2 b V 1 a − Y 22 V 2 b V 2 a . = Y 12 V 1 a V 2 b − Y 12 V 1 b V 2 a + Y 21 V 1 b V 2 a − Y 21 V 1 a V 2 b = ( Y 12 − Y 21 ) V 1 a V 2 b + ( − Y 12 + Y 21 ) V 1 b V 2 a = ( Y 12 − Y 21 ) V 1 a V 2 b − ( Y 12 − Y 21 ) V 1 b V 2 a = ( Y 12 − Y 21 ) ( V 1 a V 2 b − V 1 b V 2 a ) . \\begin{aligned} \& V_{1a} I_{1b} - V_{1b} I_{1a} + V_{2a} I_{2b} - V_{2b} I_{2a} \\\\ \&= Y_{11} V_{1a} V_{1b} + Y_{12} V_{1a} V_{2b} - Y_{11} V_{1b} V_{1a} - Y_{12} V_{1b} V_{2a} \\\\ \&\\quad + Y_{21} V_{2a} V_{1b} + Y_{22} V_{2a} V_{2b} - Y_{21} V_{2b} V_{1a} - Y_{22} V_{2b} V_{2a}.\\\\ \&= Y_{12} V_{1a} V_{2b} - Y_{12} V_{1b} V_{2a} + Y_{21} V_{1b} V_{2a} - Y_{21} V_{1a} V_{2b} \\\\ \&= (Y_{12} - Y_{21}) V_{1a} V_{2b} + (-Y_{12} + Y_{21}) V_{1b} V_{2a} \\\\ \&= (Y_{12} - Y_{21}) V_{1a} V_{2b} - (Y_{12} - Y_{21}) V_{1b} V_{2a} \\\\ \&= (Y_{12} - Y_{21}) (V_{1a} V_{2b} - V_{1b} V_{2a}). \\end{aligned} V1aI1b−V1bI1a+V2aI2b−V2bI2a=Y11V1aV1b+Y12V1aV2b−Y11V1bV1a−Y12V1bV2a+Y21V2aV1b+Y22V2aV2b−Y21V2bV1a−Y22V2bV2a.=Y12V1aV2b−Y12V1bV2a+Y21V1bV2a−Y21V1aV2b=(Y12−Y21)V1aV2b+(−Y12+Y21)V1bV2a=(Y12−Y21)V1aV2b−(Y12−Y21)V1bV2a=(Y12−Y21)(V1aV2b−V1bV2a). ( V 1 a V 2 b − V 1 b V 2 a ) ( Y 12 − Y 21 ) = 0 ( 4.35 ) (V_{1a} V_{2b} - V_{1b} V_{2a})(Y_{12} - Y_{21}) = 0 \\quad (4.35) (V1aV2b−V1bV2a)(Y12−Y21)=0(4.35) 源a和b相互独立,电压 V 1 a V_{1a} V1a, V 1 b V_{1b} V1b, V 2 a V_{2a} V2a和 V 2 b V_{2b} V2b可取任意值。因此,要使式(4.35)对任意选择的源都成立,须有 Y 12 = Y 21 Y_{12} = Y_{21} Y12=Y21,又因为标为1和2的端口是任选的,于是得到通用结果 Y i j = Y j i ( 4.36 ) Y_{ij} = Y_{ji} \\quad (4.36) Yij=Yji(4.36) 因此,若Y是对称矩阵,则它的逆矩阵Z也是对称的。 #### 4.2.2 无耗网络 现在讨论**互易的无耗N端口结,**并证明阻抗和导纳矩阵元素必须是纯虚数。若网络是无耗的,则输送到网络的净实功率为零(即进出的功率流相等,网络不消耗功率)。这样, Re { P a v g } = 0 \\operatorname{Re}\\left\\{P_{avg}\\right\\}=0 Re{Pavg}=0,其中(电压电流为列向量,Z的转置由于互易等于本身): P avg = 1 2 V t I ∗ = 1 2 ( Z I ) t I ∗ = 1 2 I t Z I ∗ P_{\\text{avg}}=\\frac{1}{2} V\^{t} I\^{\*}=\\frac{1}{2}(Z I)\^{t} I\^{\*}=\\frac{1}{2} I\^{t} Z I\^{\*} Pavg=21VtI∗=21(ZI)tI∗=21ItZI∗ = 1 2 ( I 1 Z 11 I 1 ∗ + I 1 Z 12 I 2 ∗ + I 2 Z 21 I 1 ∗ + ⋯ ) =\\frac{1}{2}\\left(I_{1} Z_{11} I_{1}\^{\*}+I_{1} Z_{12} I_{2}\^{\*}+I_{2} Z_{21} I_{1}\^{\*}+\\cdots\\right) =21(I1Z11I1∗+I1Z12I2∗+I2Z21I1∗+⋯) = 1 2 ∑ n = 1 N ∑ m = 1 N I m Z m n I n ∗ =\\frac{1}{2} \\sum_{n=1}\^{N} \\sum_{m=1}\^{N} I_{m} Z_{m n} I_{n}\^{\*} =21n=1∑Nm=1∑NImZmnIn∗ 式中用到了矩阵代数的结果 ( A B ) = B t A t (AB)=B\^{t}A\^{t} (AB)=BtAt。因为各个 I n I_{n} In是独立的,要满足功率的实部为零必须让每个自乘项 ( I n Z n n I n ∗ ) \\left(I_{n} Z_{nn} I_{n}\^{\*}\\right) (InZnnIn∗)的实部等于零,由于各个电流具有**独立**的地位,为了通用性,讨论第n项电流不为零的情况,**其他所有端口的电流可暂时不管**。所以有 Re { I n Z n n I n ∗ } = ∣ I n ∣ 2 Re { Z n n } = 0 \\operatorname{Re}\\left\\{I_{n} Z_{nn} I_{n}\^{\*}\\right\\}=\\left\|I_{n}\\right\|\^{2} \\operatorname{Re}\\left\\{Z_{nn}\\right\\}=0 Re{InZnnIn∗}=∣In∣2Re{Znn}=0 或 Re { Z n n } = 0 ( 4.38 ) \\operatorname{Re}\\left\\{Z_{nn}\\right\\}=0 \\quad (4.38) Re{Znn}=0(4.38) 可以根据(4.38)推广对任意的电流 I m I_{m} Im和 I n I_{n} In**(其他电流为零时)**,有 Re { ( I n I m ∗ + I m I n ∗ ) Z m n } = 0 \\operatorname{Re}\\left\\{\\left(I_{n} I_{m}\^{\*}+I_{m} I_{n}\^{\*}\\right) Z_{mn}\\right\\}=0 Re{(InIm∗+ImIn∗)Zmn}=0 因为互易有 Z m n = Z n m Z_{mn}=Z_{nm} Zmn=Znm。然而, ( I n I m ∗ + I m I n ∗ ) \\left(I_{n} I_{m}\^{\*}+I_{m} I_{n}\^{\*}\\right) (InIm∗+ImIn∗)是纯实量,一般它不为零。这样,就必须有 Re { Z m n } = 0 ( 4.39 ) \\operatorname{Re}\\left\\{Z_{mn}\\right\\}=0 \\quad (4.39) Re{Zmn}=0(4.39) 因此,式(4.38)和式(4.39)表明,对任意m,n有 Re { Z m n } = 0 \\operatorname{Re}\\left\\{Z_{mn}\\right\\}=0 Re{Zmn}=0。读者可以证明这还会导致一个虚矩阵Y。 ### 例题4.3 阻抗参量的计算 求图4.6所示二端口T形网络的Z参量。 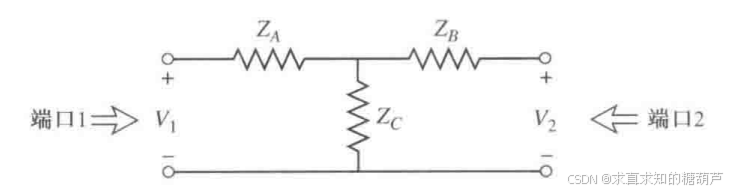 **图4.6 二端口T形网络** 解:由式(4.28)可知, Z 11 Z_{11} Z11是端口2开路时端口1的输入阻抗: Z 11 = V 1 I 1 ∣ I 2 = 0 = Z A + Z C Z_{11}=\\left.\\frac{V_{1}}{I_{1}}\\right\|_{I_{2}=0}=Z_{A}+Z_{C} Z11=I1V1 I2=0=ZA+ZC 当电流 I 2 I_{2} I2加到端口2时测量端口1上的开路电压,就可求出转移阻抗 Z 12 Z_{12} Z12。利用电阻上的分压可得 Z 12 = V 1 I 2 ∣ I 1 = 0 = V 2 I 2 Z C Z B + Z C = Z C Z_{12}=\\left.\\frac{V_{1}}{I_{2}}\\right\|_{I_{1}=0}=\\frac{V_{2}}{I_{2}}\\frac{Z_{C}}{Z_{B}+Z_{C}}=Z_{C} Z12=I2V1 I1=0=I2V2ZB+ZCZC=ZC 读者可自行证明 Z 12 = Z 21 Z_{12}=Z_{21} Z12=Z21,这表明电路是互易的。最后, Z 22 Z_{22} Z22求出为 Z 22 = V 2 I 2 ∣ I 1 = 0 = Z B + Z C Z_{22}=\\left.\\frac{V_{2}}{I_{2}}\\right\|_{I_{1}=0}=Z_{B}+Z_{C} Z22=I2V2 I1=0=ZB+ZC