GCN and Mamba的 理论相似性

0泡2026-01-28 8:29

GCN and Mamba的 理论相似性

持续更新ing

文章目录

信号处理

  • N 维向量空间
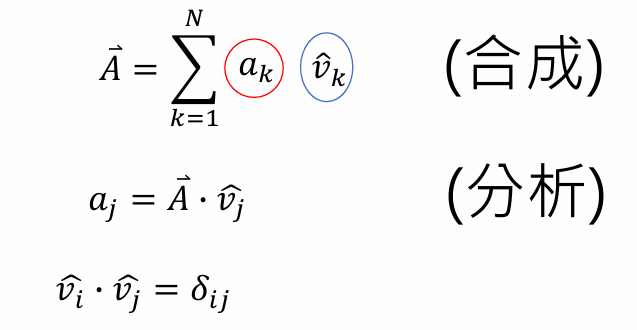
  • a k a_k ak的定义
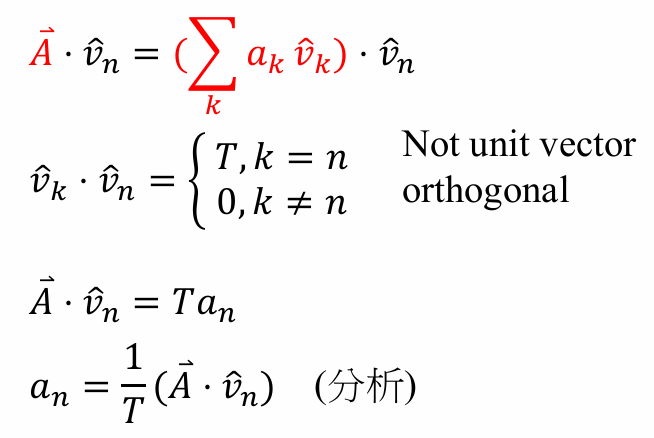
  • 时域与频域的信号表达式

傅里叶变换

傅里叶变换认为，世界上的任何一段波（无论多复杂），都可以看作是一堆简单的"正弦波"叠加而成的。

  • 傅里叶变换 (FT) ：是**"拆解"**的过程。把时域信号拆解为频域信号。
  • 逆傅里叶变换 (IFT) ：是**"重组"**的过程。把频域信号还原为时域信号。

傅里叶变换 (FT)：从时间到频率 (The Decomposition)

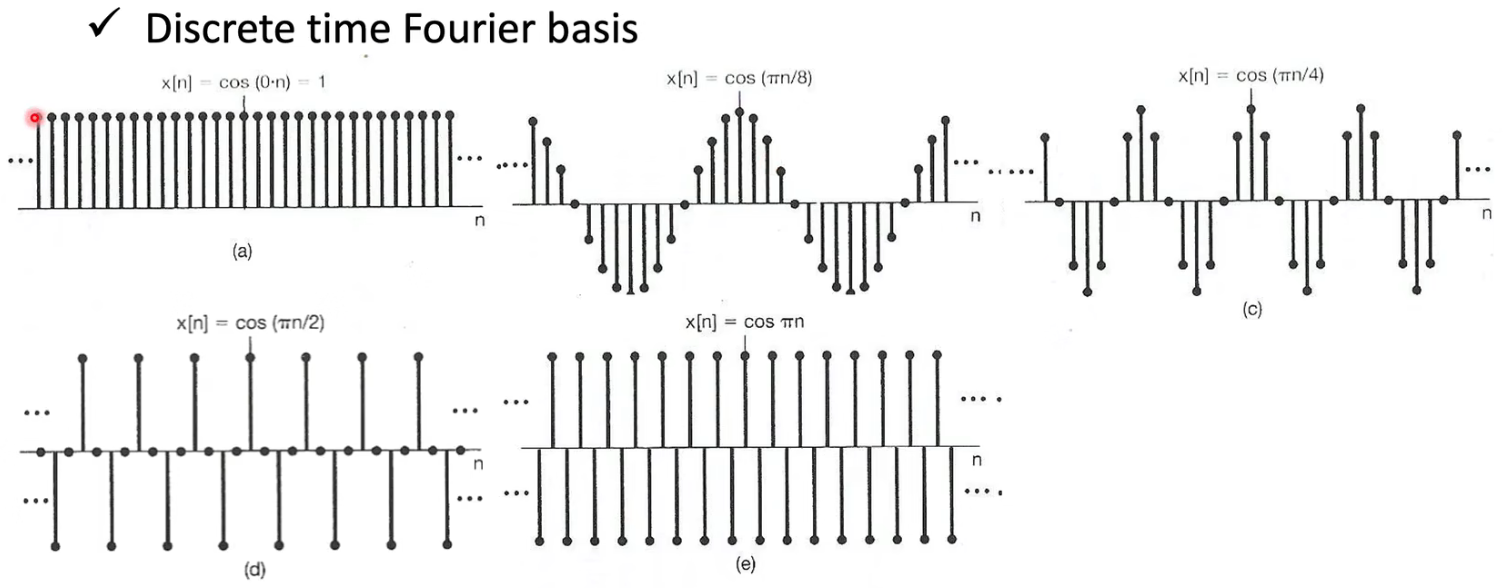
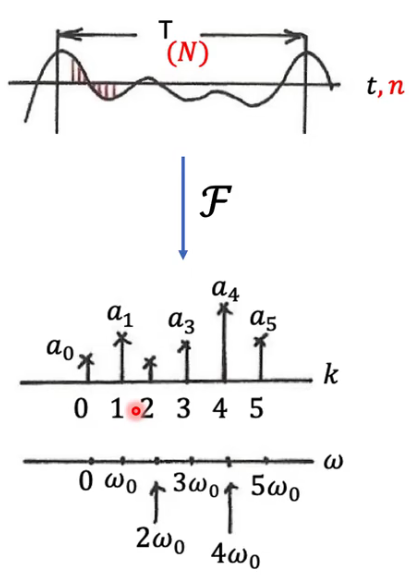
目标 ：把一个随时间变化的信号 f ( t ) f(t) f(t)（比如一段录音波形），转换成随频率变化的函数 F ( ω ) F(\omega) F(ω)（比如乐谱）。

数学公式

F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t   d t F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} \, dt F(ω)=∫−∞∞f(t)e−iωtdt

  • f ( t ) f(t) f(t)：原始信号。
  • e − i ω t e^{-i\omega t} e−iωt："筛子"。根据欧拉公式 e − i x = cos ⁡ x − i sin ⁡ x e^{-ix} = \cos x - i\sin x e−ix=cosx−isinx，它代表一个频率为 ω \omega ω 的螺旋线（或正弦波）。
  • 积分 ∫ \int ∫：就是计算"内积"或"相关性"。它在问："信号 f ( t ) f(t) f(t) 和频率 ω \omega ω 的正弦波有多像？"
    • F ( ω ) F(\omega) F(ω)：结果。它告诉我们在频率 ω \omega ω 处，信号的振幅 （有多响）和相位（什么时候开始响）。

逆傅里叶变换 (IFT)：从频率到时间 (The Reconstruction)

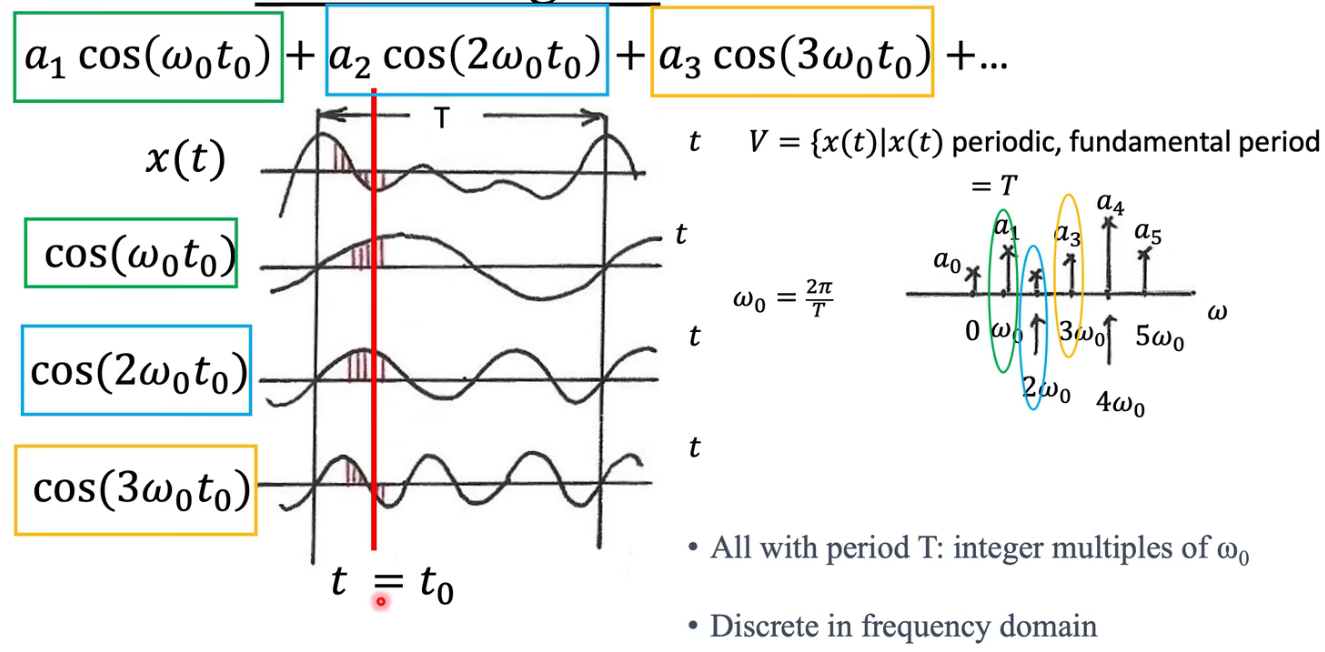
目标 ：已知每个频率的成分 F ( ω ) F(\omega) F(ω)，把它们加起来，还原回原始波形 f ( t ) f(t) f(t)。

数学公式

f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t   d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i\omega t} \, d\omega f(t)=2π1∫−∞∞F(ω)eiωtdω

  • F ( ω ) F(\omega) F(ω)：配方表（各个频率的权重）。
  • e i ω t e^{i\omega t} eiωt：原材料（各个频率的正弦波）。
  • 积分 ∫ \int ∫：把所有原材料按照配方表加起来（叠加）。
  • f ( t ) f(t) f(t)：还原出的原始信号。

为什么要提到它？与 Mamba/S4 的关系

在你之前关于 Mamba 的问题中，我们提到了 FFT（快速傅里叶变换）和卷积定理。

  • 卷积定理：时域上的卷积 = 频域上的乘法。

Convolution ( f , g ) ↔ F ( ω ) ⋅ G ( ω ) \text{Convolution}(f, g) \leftrightarrow F(\omega) \cdot G(\omega) Convolution(f,g)↔F(ω)⋅G(ω)

  • S4 的策略：

S4 是线性时不变系统（LTI），它的计算本质是卷积。卷积很难算（ O ( N 2 ) O(N^2) O(N2)）。

所以 S4 先用 FT 把信号变成频谱，做简单的乘法（ O ( N ) O(N) O(N)），再用 IFT 变回来。这大大加速了计算。

  • Mamba 的策略：

Mamba 的参数是随时间变的（不是 LTI），所以不能用卷积定理，也就不能用 FFT 加速。因此，Mamba 被迫发明了**"并行扫描 (Parallel Scan)"** 算法来替代 FFT 的地位。

GCN------Spectral Graph Theory

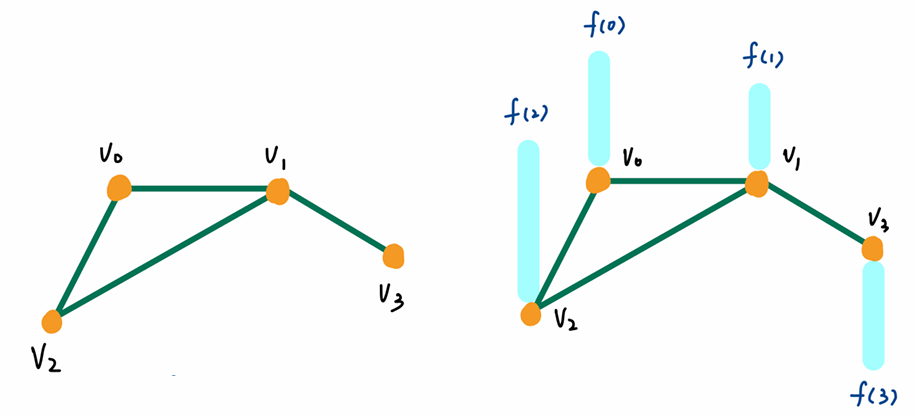
图定义

  • 图的特征定义
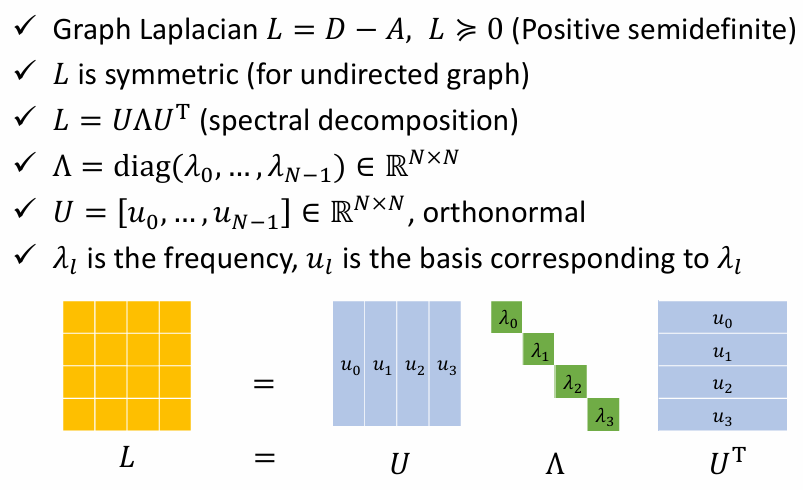
  • example

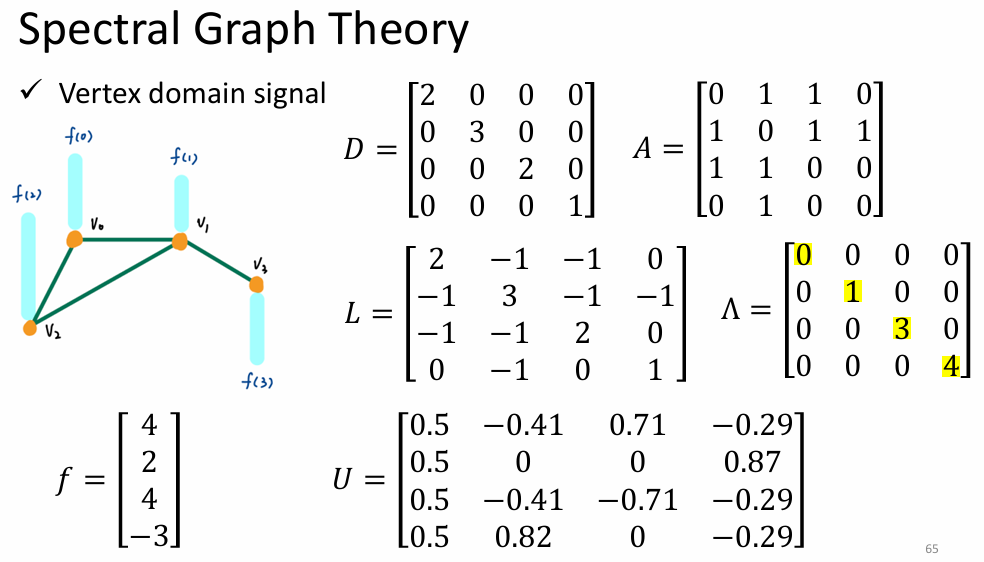
图谱理论中的低频与高频

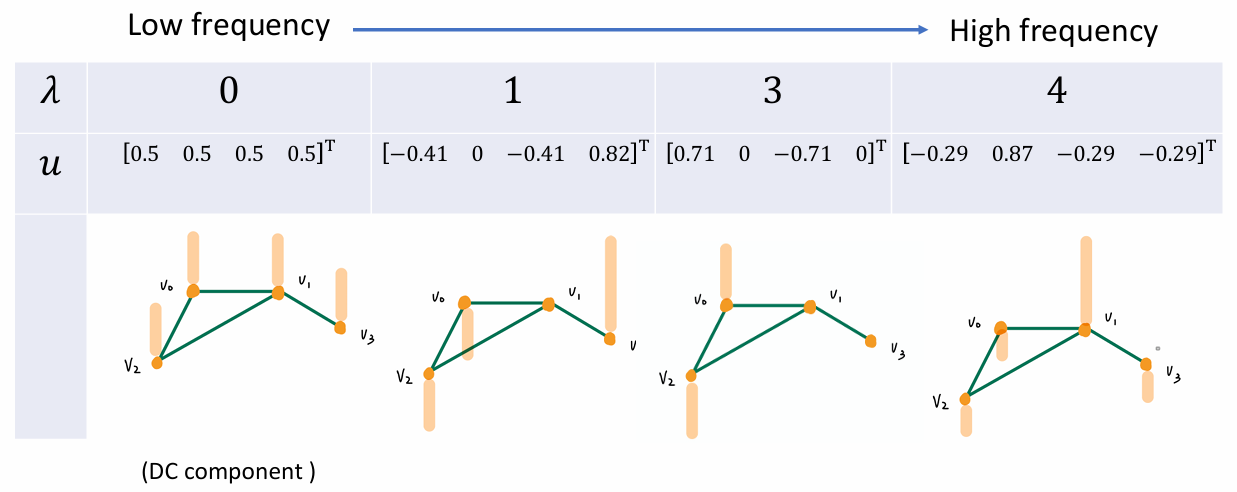
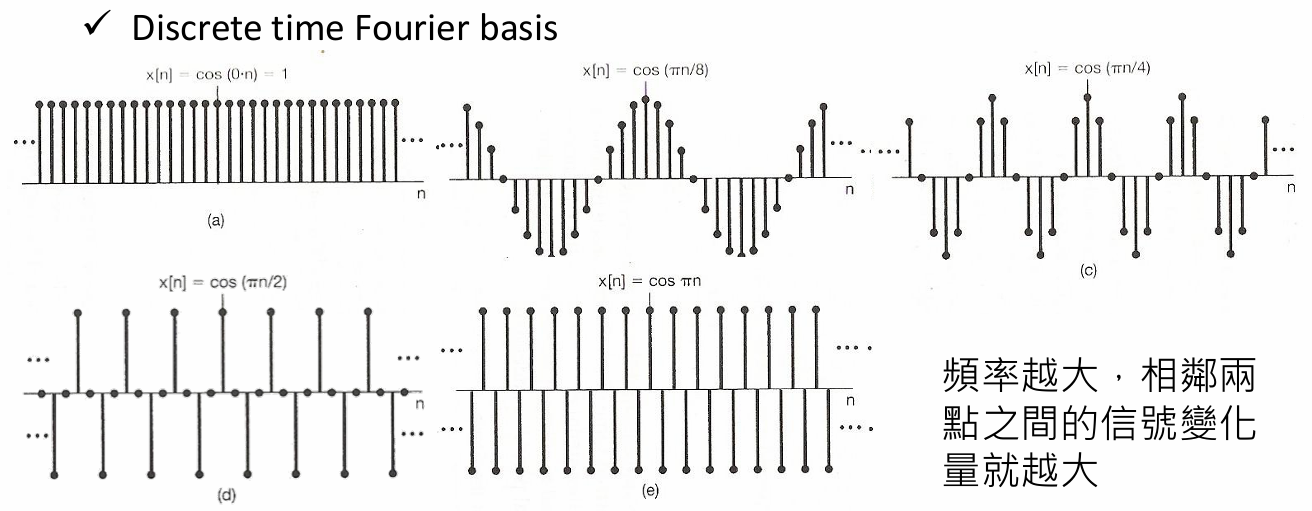
节点频率的解释

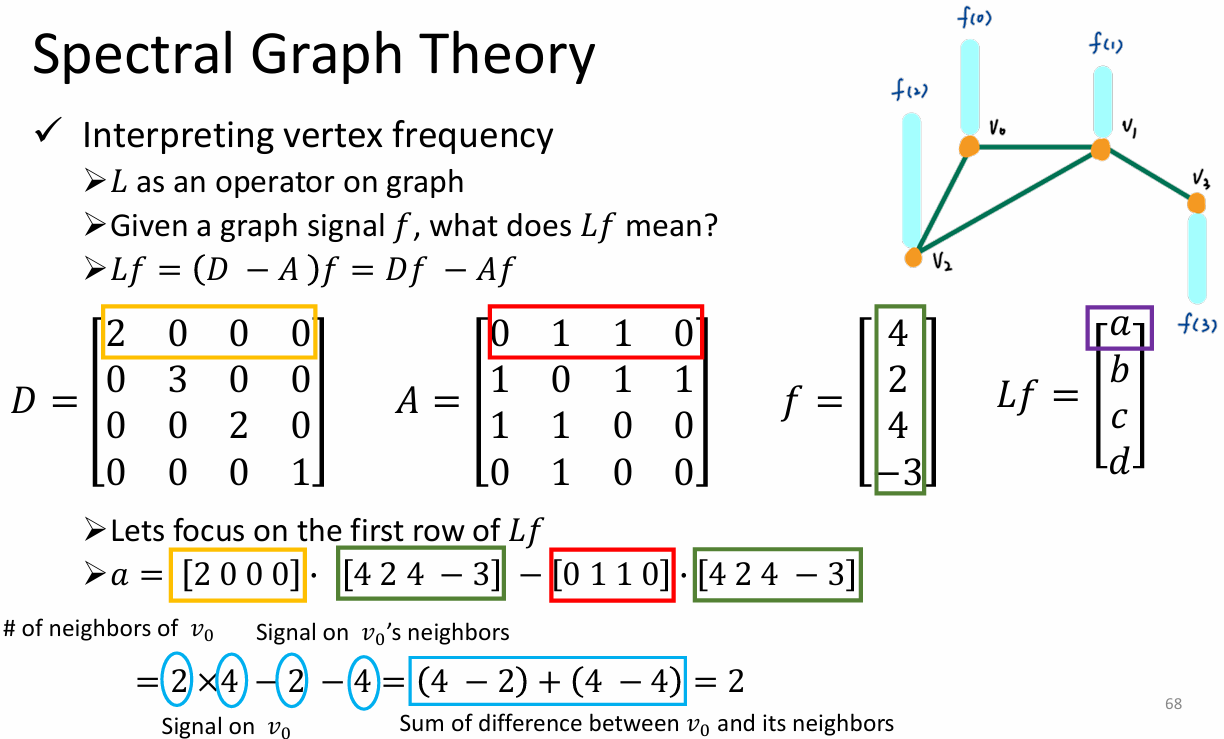
TODO：这里的 Power 和 Mamba 里的概率度量有没有什么联系？

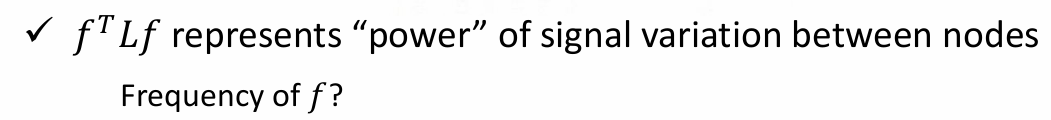
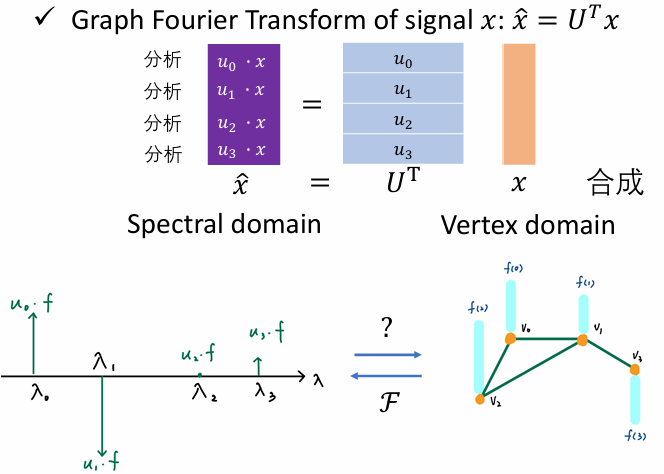
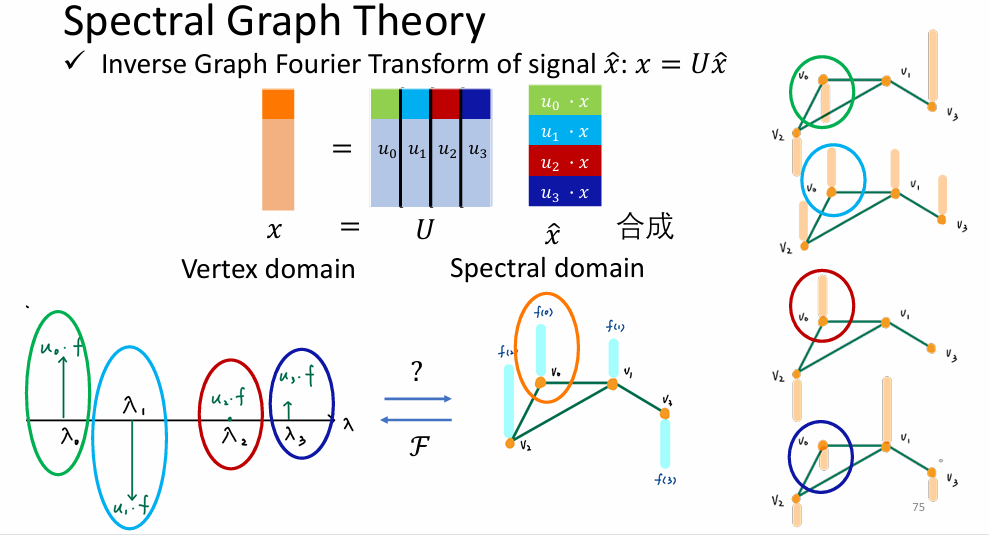
图信号傅里叶变换与逆变换

  • 傅里叶变换
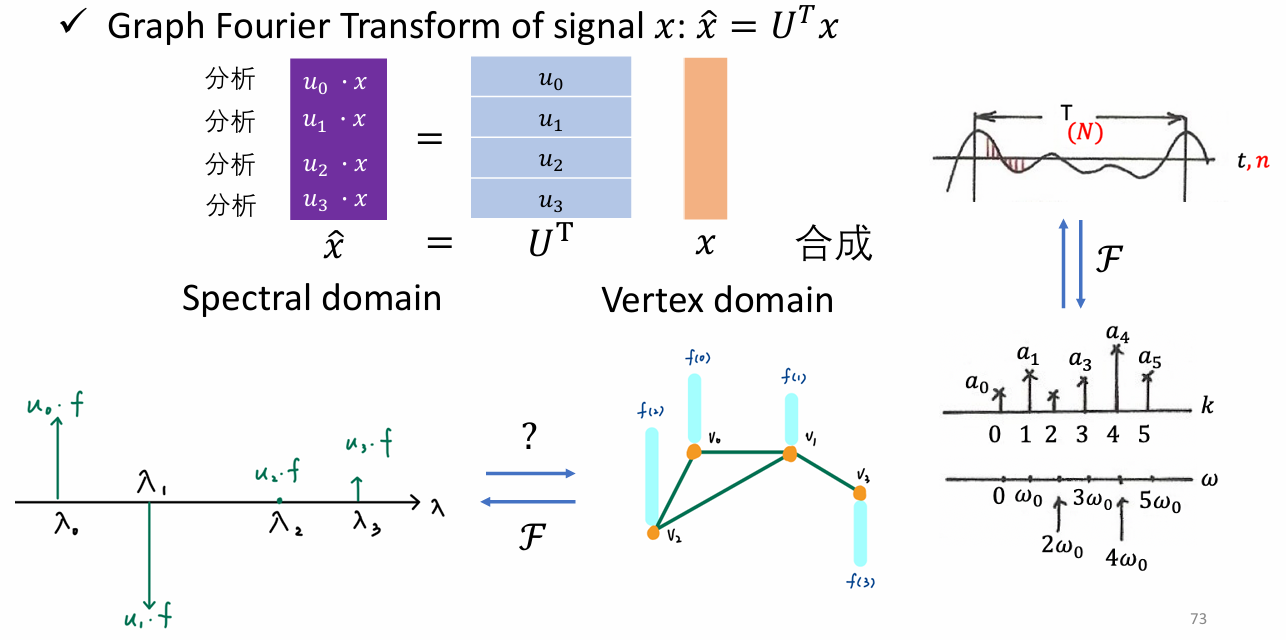
  • 逆傅里叶变换

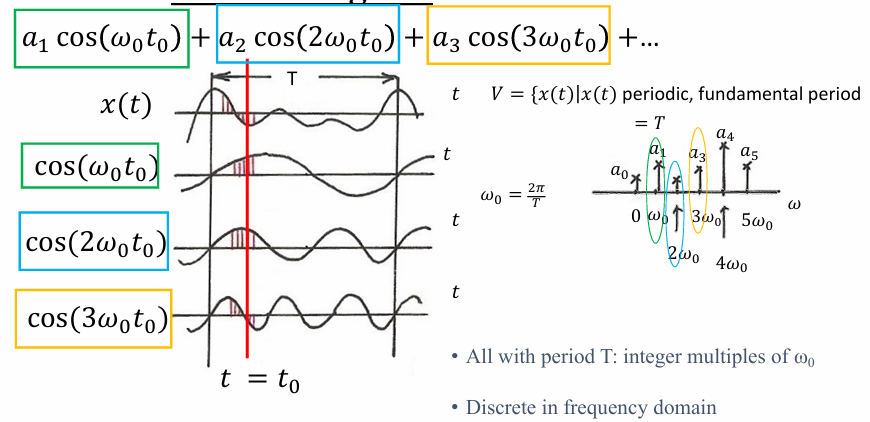
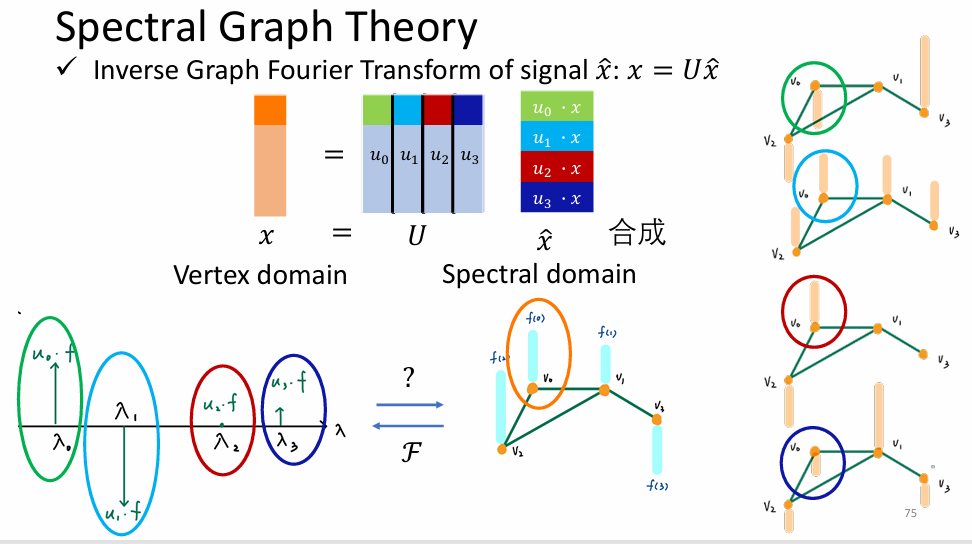
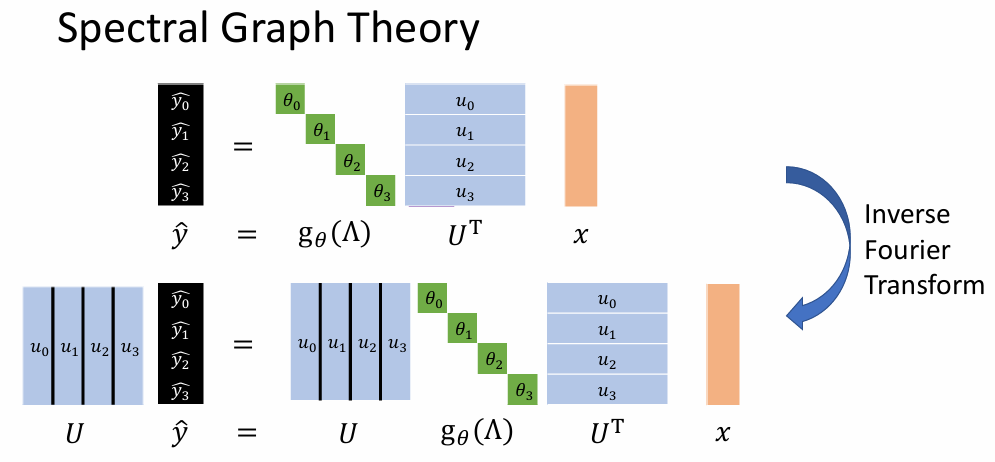
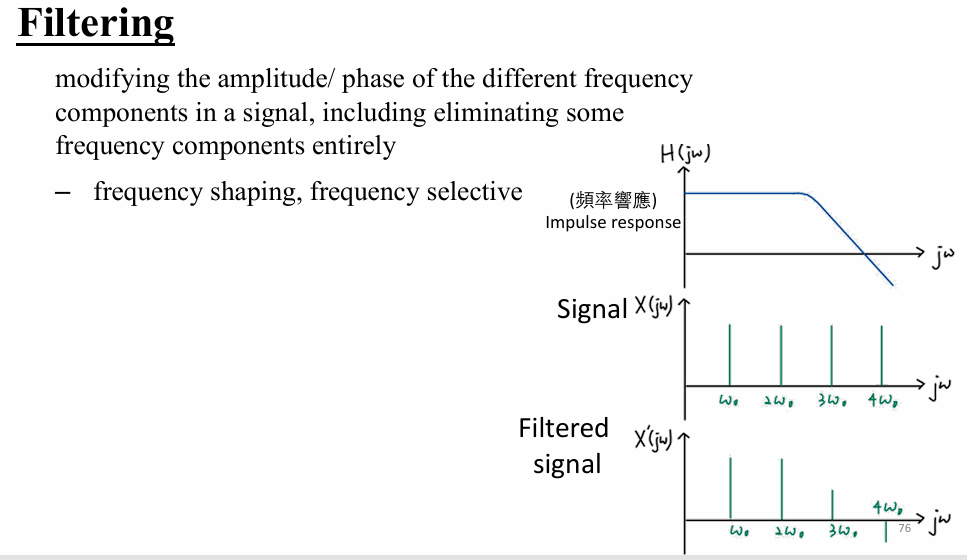
图信号的过滤

  • Filtering
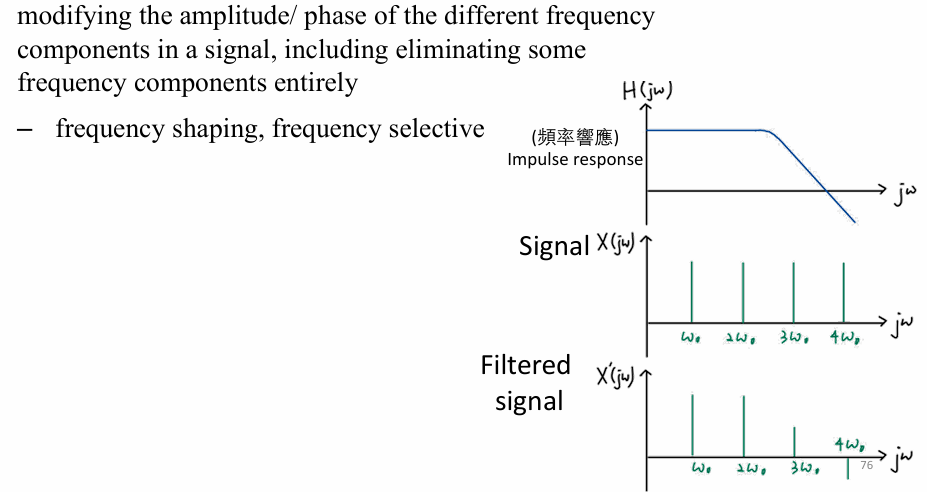
  • 图谱信号过滤

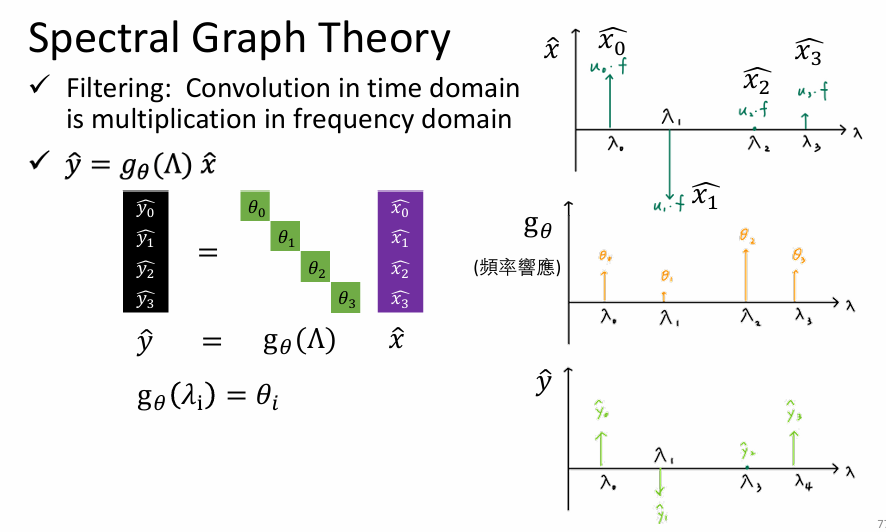
这里的过滤其实就是在做注意力机制的过程！他从频率的角度聚合历史信号，筛选有用的频率信号。

  • 图谱信号过滤后逆傅里叶变换
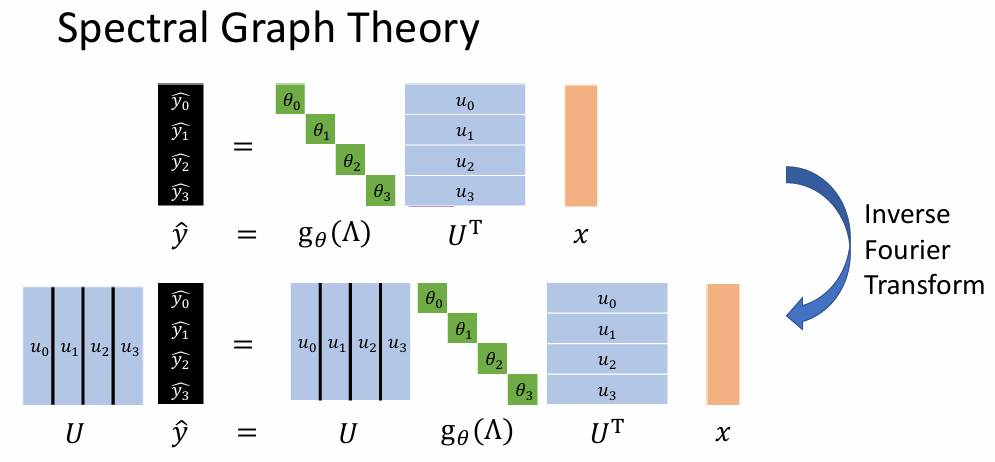
  • 图谱理论中过滤函数（频率反应）的选择------问题 1：学习复杂度与输入长度线性相关
  • 图谱理论中过滤函数（频率反应）的选择------问题 2：信号卷积过程非 localize（即聚合了其他非相关节点）

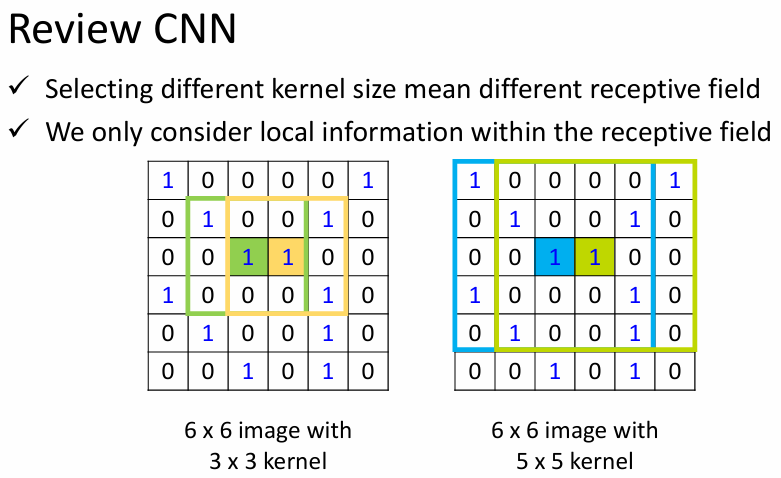
ChebNet------Chebyshev 多项式递归

https://arxiv.org/pdf/1606.09375.pdf

  • 针对问题 1、2 的解决方案------多项式参数

只用学多项式函数的系数就可以了。

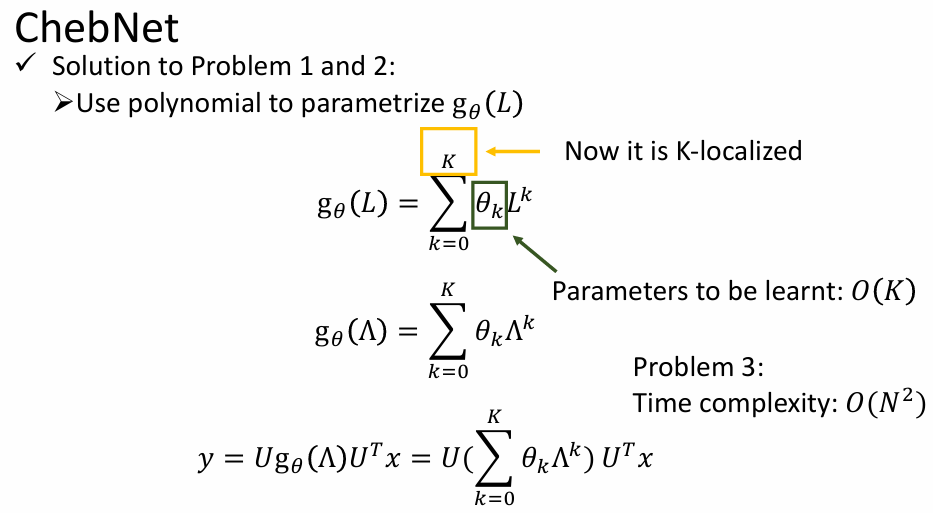
出现问题 3：时间复杂度为 O ( N 2 ) O(N^2) O(N2)

  • 针对问题 3 的解决方案------Chebyshev 多项式
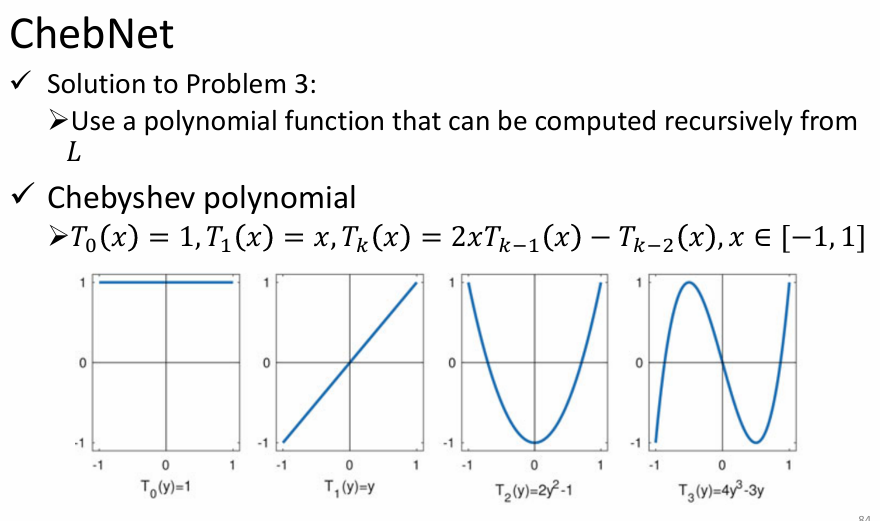
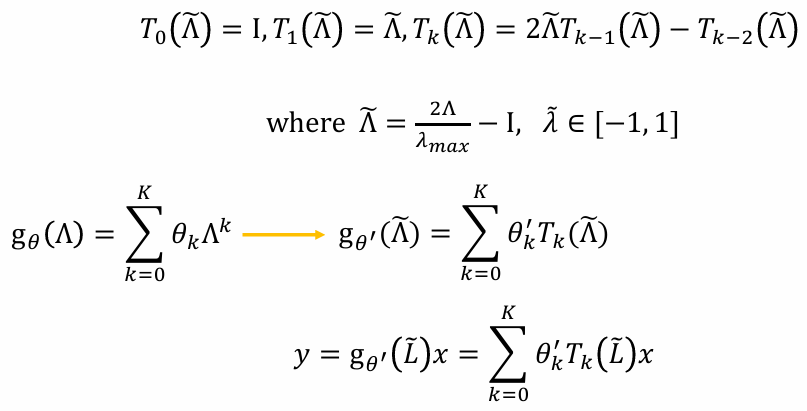
  • 可以递归的多项式的好处是什么呢？

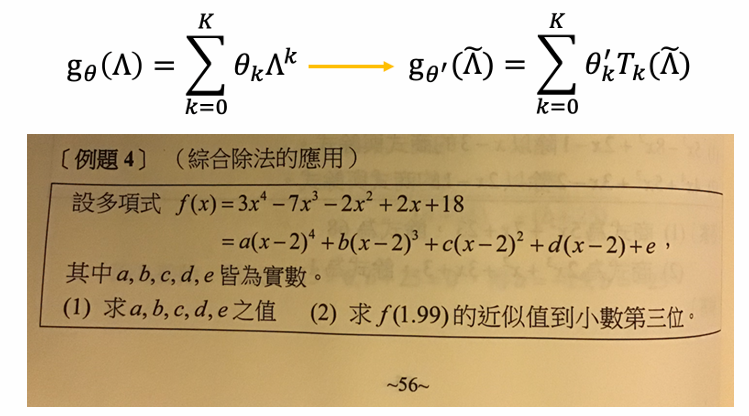
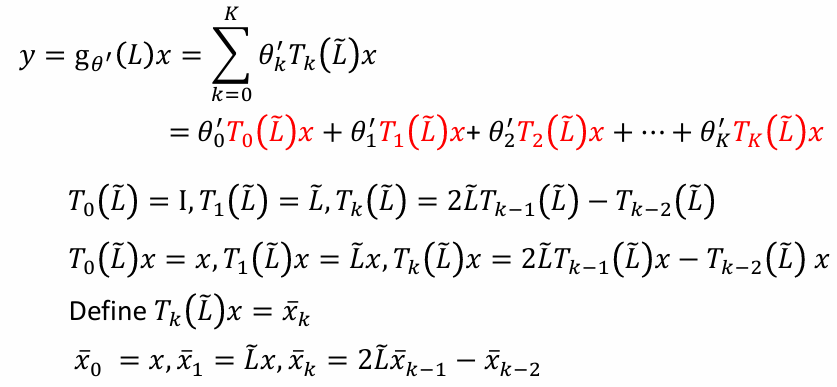
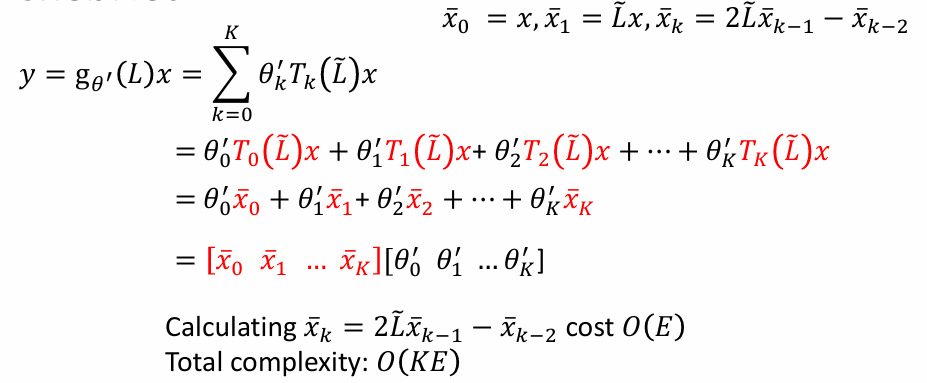
GCN------renormalization trick

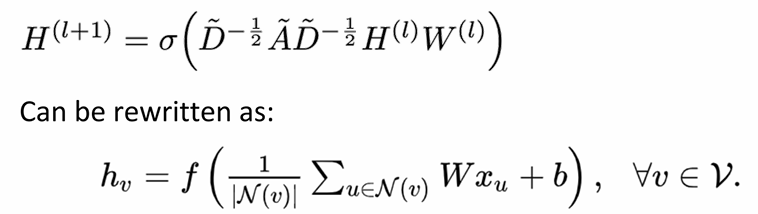
SSM/S4/HiPPO/Mamba

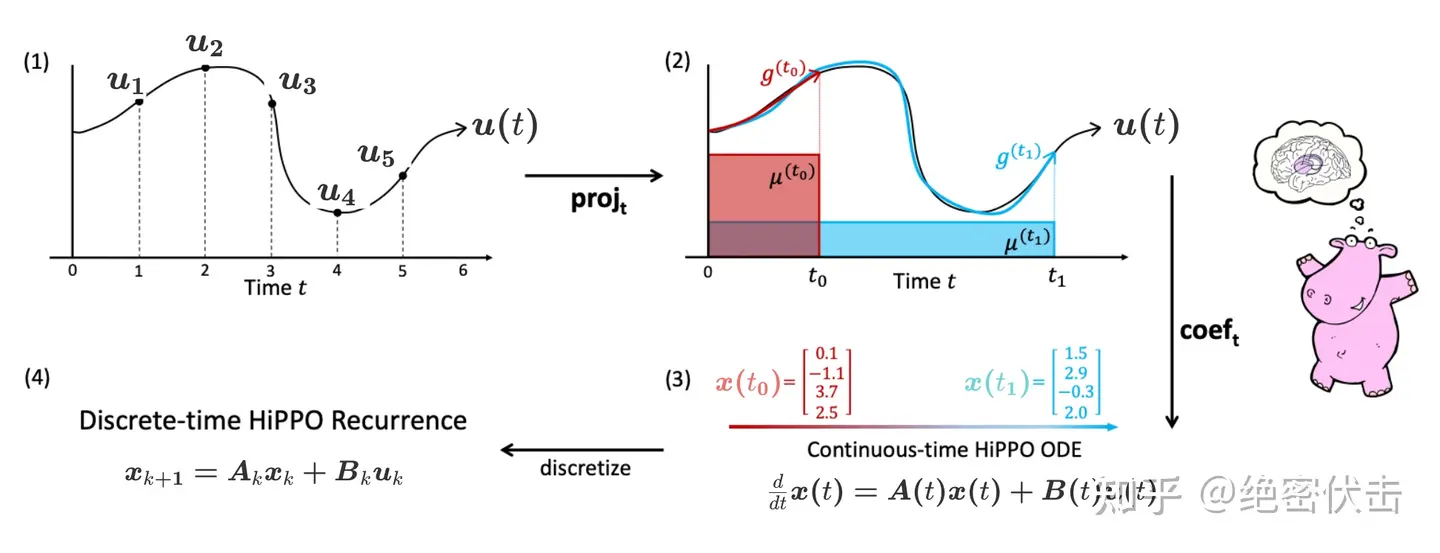
为了彻底理解 Mamba 的底层逻辑，将这个过程拆解为四个阶段：函数逼近（投影） → \to →微分方程推导（HiPPO） → \to →离散化（SSM） → \to →选择性参数化（Mamba）。

第一阶段：投影与系数提取

目标 ：将一段连续的历史函数 f ( τ ) f(\tau) f(τ)（其中 τ ≤ t \tau \le t τ≤t），压缩成一个有限维的向量 c ( t ) c(t) c(t)。

定义测度*(Measure)*与空间

Mamba (基于 HiPPO-LegS) 关心的是过去 [ 0 , t ] [0, t] [0,t] 窗口内的所有信息，且权重相等。我们定义缩放勒让德测度 (Scaled Legendre Measure, LegS）：

μ ( t ) ( x ) = 1 t I [ 0 , t ] ( x ) \mu^{(t)}(x) = \frac{1}{t} \mathbb{I}_{[0, t]}(x) μ(t)(x)=t1I[0,t](x)

  • 这表示在区间 [ 0 , t ] [0, t] [0,t] 上是均匀分布，密度为 1 / t 1/t 1/t。
定义基底*(Basis)*

在这个测度下，我们要寻找一组正交多项式基底 P n ( t ) ( x ) P_n^{(t)}(x) Pn(t)(x)。数学上对应的就是移位勒让德多项式*(Shifted Legendre Polynomials)*。

它们满足正交性：

⟨ P n ( t ) , P m ( t ) ⟩ μ ( t ) = ∫ 0 t P n ( t ) ( x ) P m ( t ) ( x ) 1 t d x = δ n m \langle P_n^{(t)}, P_m^{(t)} \rangle_{\mu^{(t)}} = \int_0^t P_n^{(t)}(x) P_m^{(t)}(x) \frac{1}{t} dx = \delta_{nm} ⟨Pn(t),Pm(t)⟩μ(t)=∫0tPn(t)(x)Pm(t)(x)t1dx=δnm

这里的 δ n m \delta_{nm} δnm是数学中一个非常著名的符号，叫做 克罗内克 δ \delta δ 函数 _(Kronecker Delta)_。

它的定义非常简单，就是一个**"二值开关"**：

δ n m = { 1 如果 n = m 0 如果 n ≠ m \delta_{nm} = \begin{cases} 1 & \text{如果 } n = m \\ 0 & \text{如果 } n \neq m \end{cases} δnm={10如果 n=m如果 n=m

在这个积分公式中，它代表了基函数 P n ( t ) P_n^{(t)} Pn(t)和 P m ( t ) P_m^{(t)} Pm(t)之间的正交归一性。

最优系数提取*(Projection)*

要在时刻 t t t 用一个多项式 g ( t ) ( x ) g^{(t)}(x) g(t)(x) 去逼近历史 f ( x ) f(x) f(x)，使得误差 ∫ 0 t ∣ f ( x ) − g ( t ) ( x ) ∣ 2 d μ \int_0^t |f(x) - g^{(t)}(x)|^2 d\mu ∫0t∣f(x)−g(t)(x)∣2dμ 最小。

根据希尔伯特空间投影定理，最优系数 c n ( t ) c_n(t) cn(t) 就是 f ( x ) f(x) f(x) 在基底上的内积：

c n ( t ) = ∫ 0 t f ( x ) P n ( x t ) 1 t d x \boxed{ c_n(t) = \int_0^t f(x) P_n\left(\frac{x}{t}\right) \frac{1}{t} dx } cn(t)=∫0tf(x)Pn(tx)t1dx

  • c ( t ) ∈ R N c(t) \in \mathbb{R}^N c(t)∈RN 就是隐藏状态 (Hidden State) ，即 h ( t ) h(t) h(t)。
  • 这个公式不仅提取了系数，还定义了 h ( t ) h(t) h(t) 的物理含义：积分 ∫ \int ∫就是计算"内积"或"相关性"。它在问："信号 f ( x ) f(x) f(x) 和多项式 P n ( x t ) 1 t P_n\left(\frac{x}{t}\right) \frac{1}{t} Pn(tx)t1 有多像？"

这个和傅里叶变换公式超级像！就是"广义傅里叶变换"

第二阶段：最优系数的动态变化

目标 ：每次一个输入进来，我们不能每一步都重新算上面那个积分。我们需要找到 c ˙ ( t ) \dot{c}(t) c˙(t)（系数随时间变化的导数），从而得到微分方程。

对系数求导

对 c n ( t ) c_n(t) cn(t) 关于 t t t 求导，利用莱布尼茨积分法则：

d d t c n ( t ) = d d t ∫ 0 t 1 t f ( x ) P n ( x t ) d x \frac{d}{dt} c_n(t) = \frac{d}{dt} \int_0^t \frac{1}{t} f(x) P_n\left(\frac{x}{t}\right) dx dtdcn(t)=dtd∫0tt1f(x)Pn(tx)dx

求导结果会分裂为两项：边界项 （新数据）和积分内部求导项（旧记忆维护）。

c ˙ n ( t ) = 1 t f ( t ) P n ( 1 ) ⏟ 边界项 (Term 1) + ∫ 0 t f ( x ) ∂ ∂ t [ 1 t P n ( x t ) ] d x ⏟ 内部变化项 (Term 2) \dot{c}n(t) = \underbrace{\frac{1}{t} f(t) P_n(1)}{\text{边界项 (Term 1)}} + \underbrace{\int_0^t f(x) \frac{\partial}{\partial t} \left[ \frac{1}{t} P_n\left(\frac{x}{t}\right) \right] dx}_{\text{内部变化项 (Term 2)}} c˙n(t)=边界项 (Term 1) t1f(t)Pn(1)+内部变化项 (Term 2) ∫0tf(x)∂t∂[t1Pn(tx)]dx

推导矩阵 B (边界项)
  • Term 1 代表当前时刻 x = t x=t x=t 的输入。
  • 代入 P n ( 1 ) P_n(1) Pn(1) 的性质（勒让德多项式在端点的值）： P n ( 1 ) = 2 n + 1 P_n(1) = \sqrt{2n+1} Pn(1)=2n+1 (归一化后)。
  • 这就是矩阵 B B B 的来源：

B n = 2 n + 1 B_n = \sqrt{2n+1} Bn=2n+1

推导矩阵 A (内部变化项)

我们需要计算 ∂ ∂ t [ 1 t P n ( x t ) ] \frac{\partial}{\partial t} [\frac{1}{t} P_n(\frac{x}{t})] ∂t∂[t1Pn(tx)]。利用勒让德多项式的导数性质： ( 2 n + 1 ) P n ( x ) = d d x [ P n + 1 ( x ) − P n − 1 ( x ) ] (2n+1)P_n(x) = \frac{d}{dx}[P_{n+1}(x) - P_{n-1}(x)] (2n+1)Pn(x)=dxd[Pn+1(x)−Pn−1(x)] 以及递归关系。经过一系列推导，会发现导数项可以被完美地表示为低阶多项式系数的线性组合：

Term 2 = − 1 t ∑ k = 0 n A n k c k ( t ) \text{Term 2} = -\frac{1}{t} \sum_{k=0}^{n} A_{nk} c_k(t) Term 2=−t1∑k=0nAnkck(t)

其中 A A A 是一个特定的下三角矩阵（HiPPO Matrix）：

连续时间微分方程 (ODE)

将上述两部分合并，我们得到了完美的连续时间状态方程：

c ˙ ( t ) = 1 t A c ( t ) + B f ( t ) \boxed{ \dot{c}(t) = \frac{1}{t} A c(t) + B f(t) } c˙(t)=t1Ac(t)+Bf(t)

这就是 HiPPO 赋予 Mamba 的**"数学骨架"** 。它保证了无论 t t t 怎么变， c ( t ) c(t) c(t) 永远是最优逼近系数。

第三阶段：离散化 (Discretization)

目标 ：计算机是离散的，我们需要把连续的 h ˙ = A h + B x \dot{h} = Ah + Bx h˙=Ah+Bx 变成递归公式 h t = A ˉ h t − 1 + B ˉ x t h_t = \bar{A} h_{t-1} + \bar{B} x_t ht=Aˉht−1+Bˉxt。我们使用 零阶保持 (Zero-Order Hold, ZOH) 假设：假设在时间步长 Δ \Delta Δ 内，输入 x ( t ) x(t) x(t) 保持不变。

积分求解

在区间 [ t , t + Δ ] [t, t+\Delta] [t,t+Δ] 上求解微分方程：

h ( t + Δ ) = e Δ A h ( t ) + ∫ t t + Δ e ( t + Δ − τ ) A B x ( τ ) d τ h(t+\Delta) = e^{\Delta A} h(t) + \int_t^{t+\Delta} e^{(t+\Delta-\tau)A} B x(\tau) d\tau h(t+Δ)=eΔAh(t)+∫tt+Δe(t+Δ−τ)ABx(τ)dτ

2. 导出离散参数

由于假设 x ( τ ) x(\tau) x(τ) 在该区间是常数 x k x_k xk，可以提取出来：

  • 状态转移矩阵 A ˉ \bar{A} Aˉ：

A ˉ = exp ⁡ ( Δ A ) \bar{A} = \exp(\Delta A) Aˉ=exp(ΔA)

  • 输入矩阵 B ˉ \bar{B} Bˉ：

B ˉ = ( ∫ 0 Δ e τ A d τ ) B = A − 1 ( e Δ A − I ) B \bar{B} = \left( \int_0^\Delta e^{\tau A} d\tau \right) B = A^{-1} (e^{\Delta A} - I) B Bˉ=(∫0ΔeτAdτ)B=A−1(eΔA−I)B

最终得到 SSM 的标准递归形式：

h t = A ˉ h t − 1 + B ˉ x t \boxed{ h_t = \bar{A} h_{t-1} + \bar{B} x_t } ht=Aˉht−1+Bˉxt

第四阶段：Mamba 的选择性

目标：打破 S4 的线性时不变（LTI）限制，让参数随输入变化。

静态 vs 动态
  • S4 (静态): Δ , B , C \Delta, B, C Δ,B,C 对所有时刻 t t t 都是固定的常数。

h t = A ˉ h t − 1 + B ˉ x t h_t = \bar{A} h_{t-1} + \bar{B} x_t ht=Aˉht−1+Bˉxt

(这里的 A ˉ , B ˉ \bar{A}, \bar{B} Aˉ,Bˉ 永远不变)

  • Mamba (动态) : 参数由当前输入 x t x_t xt 生成。
参数生成公式

Δ t = Softplus ( Parameter + Linear Δ ( x t ) ) B t = Linear B ( x t ) C t = Linear C ( x t ) \begin{aligned} \Delta_t &= \text{Softplus}(\text{Parameter} + \text{Linear}{\Delta}(x_t)) \\ B_t &= \text{Linear}{B}(x_t) \\ C_t &= \text{Linear}_{C}(x_t) \end{aligned} ΔtBtCt=Softplus(Parameter+LinearΔ(xt))=LinearB(xt)=LinearC(xt)

动态离散化

因为 Δ t \Delta_t Δt 变了，每一步的离散化矩阵 A ˉ \bar{A} Aˉ 和 B ˉ \bar{B} Bˉ 都在变！

A ˉ t = exp ⁡ ( Δ t A ) B ˉ t = ( Δ t A ) − 1 ( exp ⁡ ( Δ t A ) − I ) ⋅ Δ t B t \begin{aligned} \bar{A}_t &= \exp(\Delta_t A) \\ \bar{B}_t &= (\Delta_t A)^{-1} (\exp(\Delta_t A) - I) \cdot \Delta_t B_t \end{aligned} AˉtBˉt=exp(ΔtA)=(ΔtA)−1(exp(ΔtA)−I)⋅ΔtBt

4. 最终 Mamba 工作流

h t = A ˉ t h t − 1 + B ˉ t x t \boxed{ h_t = \bar{A}t h{t-1} + \bar{B}_t x_t } ht=Aˉtht−1+Bˉtxt

y t = C t h t \boxed{ y_t = C_t h_t } yt=Ctht

总结：从数学到代码

  1. 投影 ：告诉我们需要 HiPPO 矩阵 A ，这定义了 h ( t ) h(t) h(t) 是"记忆压缩系数"。
  2. 微分 ：推导出了 h ˙ = A h + B x \dot{h} = Ah + Bx h˙=Ah+Bx 的形式，这使得我们可以用状态空间来维护这个记忆。
  3. 离散化 ：引入了 Δ \Delta Δ，将微分方程变成了计算机能跑的递归 A ˉ , B ˉ \bar{A}, \bar{B} Aˉ,Bˉ。
  4. Mamba ：让 Δ \Delta Δ随输入变化 。
    • 当 Δ t → 0 \Delta_t \to 0 Δt→0， A ˉ t → I \bar{A}_t \to I Aˉt→I（单位矩阵）， B ˉ t → 0 \bar{B}_t \to 0 Bˉt→0    ⟹    \implies ⟹保持记忆，忽略输入。
    • 当 Δ t → ∞ \Delta_t \to \infty Δt→∞， A ˉ t → 0 \bar{A}_t \to 0 Aˉt→0， B ˉ t → large \bar{B}_t \to \text{large} Bˉt→large    ⟹    \implies ⟹遗忘历史，强力写入。

GCN 与 SSM/Mamba 的相似性

要理解架构的本质联系，我们必须看它们是如何定义**"空间"，以及在这个空间上使用什么样的"算子"和"基底"**来分解和处理信息。

经典傅里叶变换

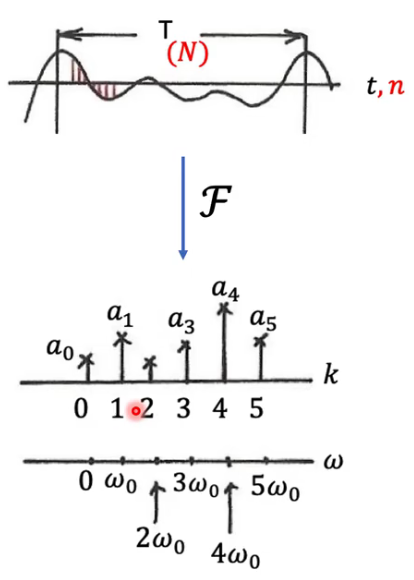
  1. F ( ω ) = ∫ − ∞ ∞ f ( t ) e − i ω t   d t F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} \, dt F(ω)=∫−∞∞f(t)e−iωtdt

  3. f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e i ω t   d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{i\omega t} \, d\omega f(t)=2π1∫−∞∞F(ω)eiωtdω

  • 物理场景：连续的欧几里得空间（比如一根无限长的直线，或者时间轴）。
  • 基函数 ： 正弦波 e − i ω t e^{-i\omega t} e−iωt。
  • 为什么选正弦波？
    • 因为正弦波是微分算子的特征函数！
      • d 2 d t 2 ( e − i ω t ) = − ω 2 e − i ω t \frac{d^2}{dt^2}(e^{-i\omega t}) = -\omega^2 e^{-i\omega t} dt2d2(e−iωt)=−ω2e−iωt。
    • 对它求导两次，它变回了自己，只多了一个常数 − ω 2 -\omega^2 −ω2（特征值）。这意味着在求导运算（LTI 系统基础）下，正弦波是最稳定的基底，可以把微积分变成简单的乘法。

图傅里叶变换

  • 物理场景：离散的非欧几里得空间（比如社交网络，节点是人，边是关系）。没有连续的"上下左右"，只有拓扑连接。
  • 基函数 ： 矩阵 L L L 的特征向量 (Eigenvectors, U U U)。
  • 为什么选这些向量？
    • 因为 L u l = λ l u l L u_l = \lambda_l u_l Lul=λlul。
    • 这些特征向量 u l u_l ul 代表了图上的"驻波"模式。
      • λ l \lambda_l λl（特征值）越小，代表这个向量在图上变化越平缓（低频，平滑信号）； λ l \lambda_l λl 越大，代表相邻节点差异剧烈（高频，噪声或边缘）。这是在不规则拓扑上定义**"频率"**的数学方式。

Mamba / HiPPO (State Space Models)

h n ( t ) = ∫ 0 t f ( x ) P n ( x t ) 1 t d x \boxed{ h_n(t) = \int_0^t f(x) P_n\left(\frac{x}{t}\right) \frac{1}{t} dx } hn(t)=∫0tf(x)Pn(tx)t1dx

h t = A ˉ h t − 1 + B ˉ x t \boxed{ h_t = \bar{A} h_{t-1} + \bar{B} x_t } ht=Aˉht−1+Bˉxt

f ( x ) ≈ ∑ n = 0 N − 1 h n ( t ) ⋅ P n ( x t ) ⋅ ( 2 n + 1 ) \boxed{ f(x) \approx \sum_{n=0}^{N-1} h_n(t) \cdot P_n\left(\frac{x}{t}\right) \cdot (2n+1) } f(x)≈n=0∑N−1hn(t)⋅Pn(tx)⋅(2n+1)

y t = C t h t \boxed{ y_t = C_t h_t } yt=Ctht

(注：具体的常数因子 ( 2 n + 1 ) (2n+1) (2n+1)取决于勒让德多项式的具体归一化定义，但核心思想是加权求和)

  • 物理场景：在线的流式历史空间。时间不断推移，我们需要把无限的过去压缩进有限的"状态"中。
  • 基函数 ： 正交多项式（主要是勒让德多项式 P n ( t ) ( x ) P_n^{(t)}(x) Pn(t)(x)）。
  • 为什么选多项式？
    • 因为它们是关于度量 μ ( t ) \mu(t) μ(t)（如 1 / t 1/t 1/t）正交的。
    • 这种正交性允许我们通过一个简单的线性递推公式（也就是 Mamba 的核心 h ˙ = A h + B x \dot{h} = Ah + Bx h˙=Ah+Bx）来实时更新系数，而不需要重新计算整个历史的积分。
    • 矩阵 A A A 本质上就是**"多项式基底在时间拉伸下的导数变换矩阵"**。它保证了我们始终在用一组最优的基底去逼近历史曲线。

Transformer (Self-Attention)

  • 物理场景 ：语义关系空间（Semantic Space）。序列中的每个 Token 都可以看作一个节点，它们之间构成了一个全连接图，但边的权重是动态的。
  • 基函数： 动态的、输入相关的基底。
  • 为什么选这种机制？
    • 与前三者不同，Transformer 不使用固定的正弦波、固定的图特征向量或固定的多项式。
    • 它通过 Q Q Q（查询）和 K K K（键）的内积，现场学习出一组基底（关注点）。
    • "语义共鸣" ：如果 Token A 和 Token B 的语义相似（ q A ⋅ k B q_A \cdot k_B qA⋅kB 大），它们就形成强连接。这相当于针对每一个具体的输入句子，现场构建了一个最适合该句子的"图傅里叶变换"，去提取特征。

RNN

  • 物理场景 ：离散的时间序列。每一步是一个离散的时刻 t t t。
  • 基底类型 ：隐式的、由权重矩阵 W W W决定的特征向量。
  • 为什么选这种机制？（以及它的痛点）
    • 机制 ：RNN 试图通过不断乘以矩阵 W W W 来把过去的信息"传递"到未来。这相当于把信息投影在 W W W 的特征向量上进行演化。
    • 痛点（梯度消失/爆炸） ：
      • 因为 W W W 是一个普通的、可学习的矩阵，它的特征值 λ \lambda λ 不受数学约束。
      • 随着时间 t t t 推移，历史信息实际上被乘以了 W t W^t Wt（矩阵的 t t t 次方）。
      • 如果特征值 ∣ λ ∣ < 1 |\lambda| < 1 ∣λ∣<1，基底衰减，记忆消失；
      • 如果特征值 ∣ λ ∣ > 1 |\lambda| > 1 ∣λ∣>1，基底膨胀，记忆爆炸。
  • 对比 Mamba ：Mamba (HiPPO) 实际上就是手动设计了一个完美的 W W W矩阵（即离散化后的 A ˉ \bar{A} Aˉ**）** ，强行保证了其特征值的数学性质能完美保留长记忆，而不是让神经网络自己去"瞎猜"一个 W W W。
相关推荐
zch不会敲代码2 小时前
深度学习之图像分类实战（食物分类）
人工智能·深度学习·分类
Coding茶水间2 小时前
基于深度学习的无人机检测系统演示与介绍(YOLOv12/v11/v8/v5模型+Pyqt5界面+训练代码+数据集)
人工智能·深度学习·yolo·目标检测·机器学习
哥布林学者11 小时前
吴恩达深度学习课程五：自然语言处理 第二周：词嵌入 课后习题与代码实践
深度学习·ai
HyperAI超神经11 小时前
加州大学构建基于全连接神经网络的片上光谱仪，在芯片级尺寸上实现8纳米的光谱分辨率
人工智能·深度学习·神经网络·机器学习·ai编程
杭州杭州杭州12 小时前
李沐动手学深度学习笔记（4）---物体检测基础
人工智能·笔记·深度学习
有Li13 小时前
学习通过皮层发育连续性迁移实现全生命周期脑解剖对应/文献速递-基于人工智能的医学影像技术
人工智能·深度学习·机器学习
狮子座明仔14 小时前
Plan-and-Act：让AI智能体学会“先想后做“
人工智能·深度学习·语言模型·自然语言处理
lixin55655616 小时前
基于迁移学习的图像风格增强器
java·人工智能·pytorch·python·深度学习·语言模型
byzh_rc16 小时前
[数学建模从入门到入土] 评价模型
网络·人工智能·深度学习·数学建模·回归·ar
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05struts2 XML外部实体注入漏洞复现（CVE-2025-68493）06UV安装并设置国内源07Open Code教程（四）| 高级配置与集成08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09Linux下V2Ray安装配置指南10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南