189.轮转数组，力扣

目录

题目

解题1：---》用链表解决-----》超时，解题失败

题解2：------》在题解一上做优化-------》7秒

题解3---》用一个数组解决---》1秒

题解4----》扩展，看题解---------》0秒

三步反转法：

步骤1：整体反转

[步骤2：反转前 k 个元素](#步骤2：反转前 k 个元素)

[步骤3：反转剩余 n-k 个元素](#步骤3：反转剩余 n-k 个元素)

---

题目

给定一个整数数组 nums，将数组中的元素向右轮转 k个位置，其中 k是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

• 1 <= nums.length <= 105
• -231 <= nums[i] <= 231 - 1
• 0 <= k <= 105

解题1：---》用链表解决-----》超时，解题失败

   public static void rotate1(int[] nums, int k) {
        // 这部分是 O(n)
        LinkedList<Integer> list = new LinkedList<>();
        for (int i = 0; i < nums.length; i++) {
            list.add(nums[i]); // O(1) 添加到链表尾部
        }

         // 这部分是 O(k * n)
        for (int i = 0; i < k; i++) {
            Integer last = list.pollLast(); // O(1) - 移除尾部
            list.add(0, last); // O(n) - 添加到头部需要遍历链表
        }

        // 这部分是 O(n)
        for (int i = 0; i < nums.length; i++) {
            nums[i] = list.get(i); // O(i) - 链表随机访问需要遍历
        }
    }

题解2：------》在题解一上做优化-------》7秒

    public static void rotate2(int[] nums, int k) {
        k = k % nums.length; // 优化：减少不必要的旋转
        if (k == 0) return;

        Deque<Integer> deque = new ArrayDeque<>();
        for (int num : nums) {
            deque.add(num); // O(1)
        }

        // 一次性旋转 k 次
        for (int i = 0; i < k; i++) {
            int last = deque.pollLast(); // O(1)
            deque.addFirst(last); // O(1) - ArrayDeque头部插入比LinkedList快
        }

        // 使用迭代器或直接索引复制，避免随机访问
        int index = 0;
        for (int num : deque) {
            nums[index++] = num; // O(1)
        }
    }

题解3---》用一个数组解决---》1秒

    public static void rotate(int[] nums, int k) {
        k = k%nums.length;
        if(k==0) return;

        int[] arr=new int[nums.length];
        int j=0;
        for (int i = nums.length-k; i < nums.length && j<nums.length; i++) {
            arr[j++]=nums[i];
        }
        for (int i = 0; i < nums.length - k; i++) {
            arr[j++]=nums[i];
        }
        //就算这里改了nums的地址，但是原main里的没有改
//        nums=arr;
        int i=0;
        for (int n :arr) {
            nums[i++]=n;
        }
    }

题解4----》扩展，看题解---------》0秒

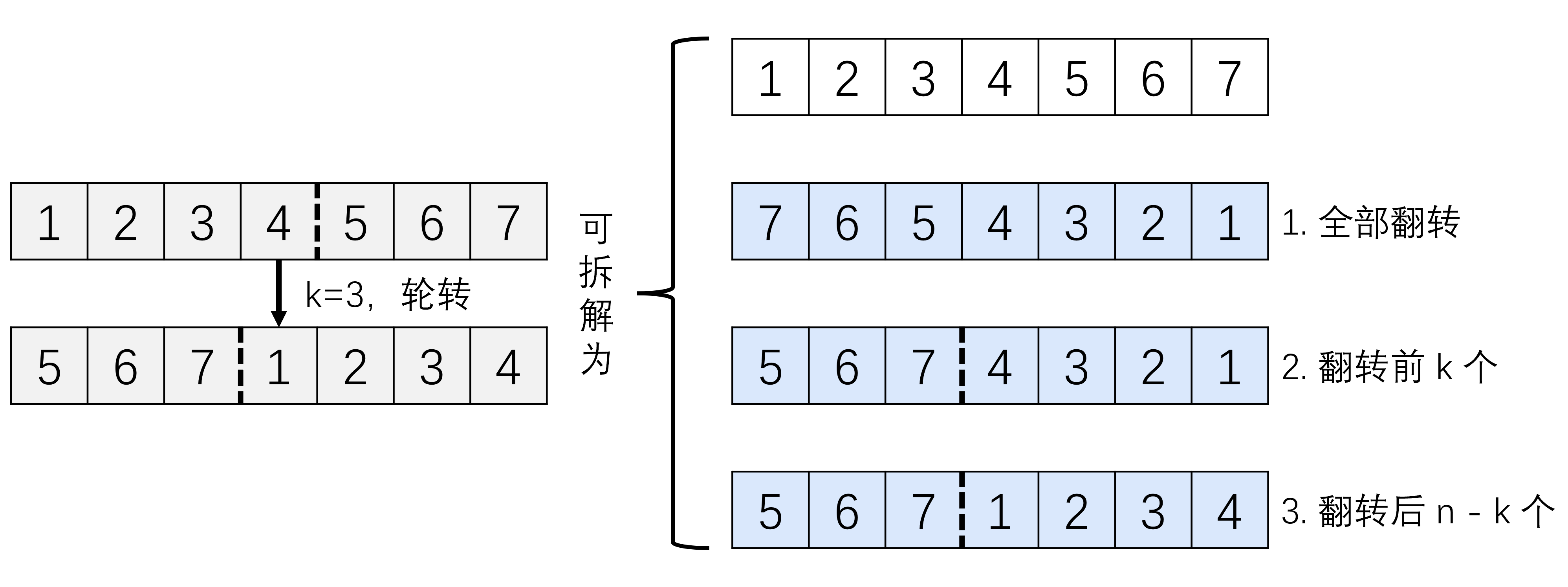
三步反转法：

步骤1：整体反转

[1,2,3,4,5,6,7] → [7,6,5,4,3,2,1]

将整个数组完全反转

步骤2：反转前 k 个元素

[7,6,5,4,3,2,1]

前 k 个元素（k=3）：[7,6,5] → [5,6,7]

得到：[5,6,7,4,3,2,1]

步骤3：反转剩余 n-k 个元素

[5,6,7,4,3,2,1]

剩余元素：[4,3,2,1] → [1,2,3,4]

最终：[5,6,7,1,2,3,4]

    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k %= n; // 关键：处理 k > n 的情况

        // 1. 整体反转
        reverse(nums, 0, n - 1);
        // 2. 反转前 k 个
        reverse(nums, 0, k - 1);
        // 3. 反转剩余部分
        reverse(nums, k, n - 1);
    }

    private void reverse(int[] nums, int i, int j) {
        while (i < j) {
            int tmp = nums[i];
            nums[i++] = nums[j];
            nums[j--] = tmp;
        }
    }